2. Boxplot

A boxplot is a graph that represents the distribution of a set of data based on some of its descriptive parameters: the median, the first quartile and the third quartile.

Example 1:

We will make a boxplot of a sample measuring 20 rods, we will do the uploading data into the system.

903.88
1020.70
934.52
860.41
936.78
1036.90
915.38
1214.10
1039.20
1087.00
1098.00
1014.50
993.45
950.38
1144.90
1011.30
1097.80
1120.20
941.83
1056.10

---

We will do the Boxplot.

Then click Calculate to get the results. You can also generate the analyses and download them in Word format.

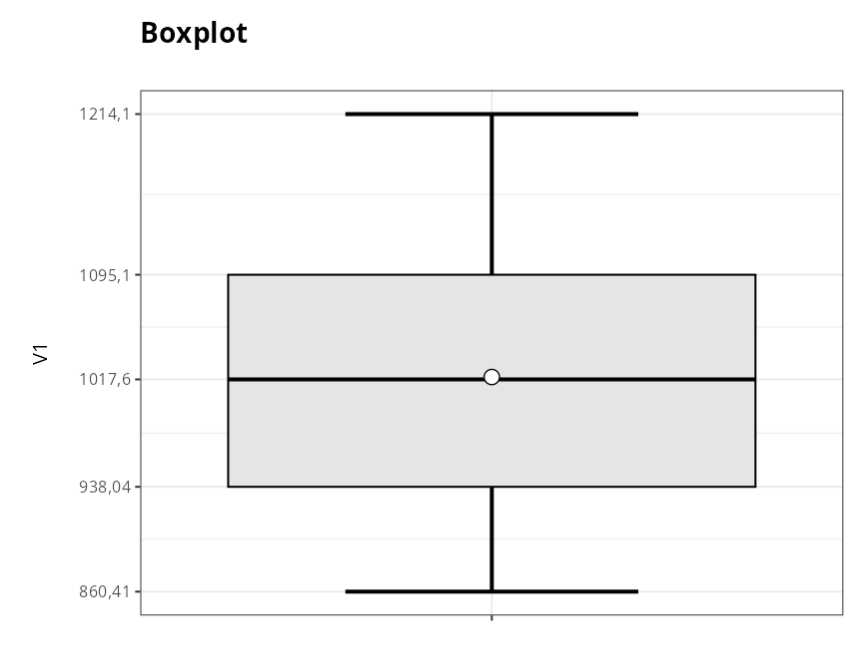
The results are:

Descriptive Summary

---

	Values
Minimum	860.410
Lower limit	860.410
First Quartile	938.043
Mean	1018.8665
Median	1017.600
Third Quartile	1095.100
Upper limit	1214.100
Maximum	1214.100

---

Example 2:

Let’s consider two types of rods, A and B, Make a Boxplot and compare the two types of rods.

Rod Type	Height
A	1036.92
A	1026.58
A	915.38
A	1034.5
A	1045.2
A	1057.42
A	1039.19
A	1099.21
A	1086.98
B	1011.26
B	1015.05
B	1002.79
B	998.45
B	1120.19
B	950
B	941.83
B	1014.54
B	1016.12

---

We will upload the data to the system.

We will then do the Boxplot

Then click Calculate to get the results. You can also generate the analyses and download them in Word format.

The results are:

Descriptive Summary

	A	B
Minimum	915.380	941.830
Lower limit	968.050	941.830
First Quartile	1030.540	974.225
Mean	1037.931	1007.803
Median	1039.190	1011.260
Third Quartile	1072.200	1015.585
Upper limit	1099.210	1077.625
Maximum	1099.210	1120.190

---

Outliers

The Order of Collection	Outliers	Groups
3	915.38	A
14	1120.19	B

---

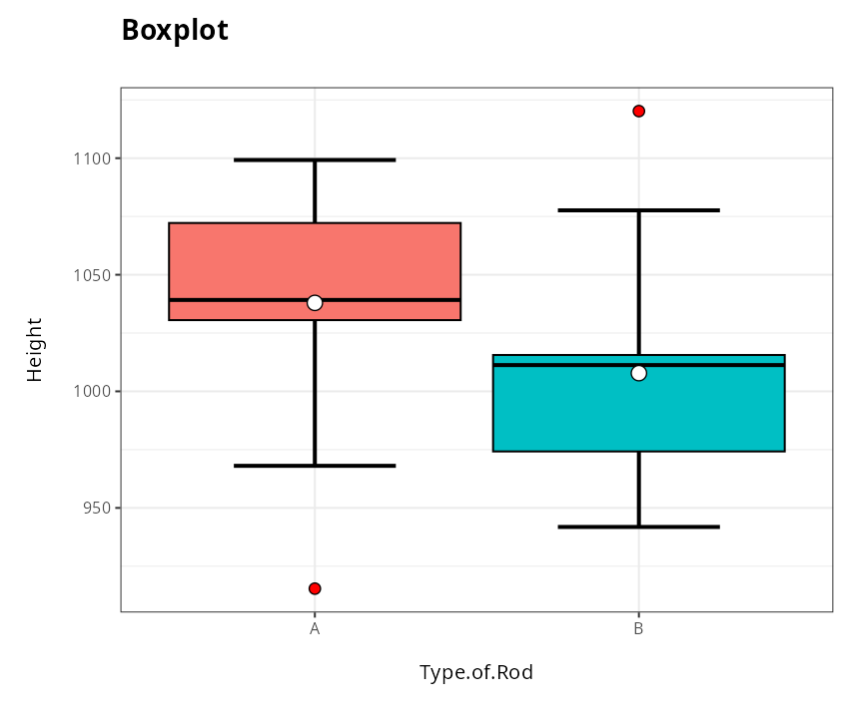
When comparing the Boxplots of the two types of rods, we see that they are behave differently in relation to their heights. Despite a of type A rods have a height value well below the heights of type B rods, the rods of this first type have heights well higher than those of the second type.