5. Seasonality Tests

Some time series exhibit a behavior known as seasonality. The seasonality of a time series is the number of observations the series takes to repeat the pattern. In the Tests tool of Seasonality, it is possible to carry out two tests to verify whether the series presents seasonality.

Example:

We will perform the test with the following data set:

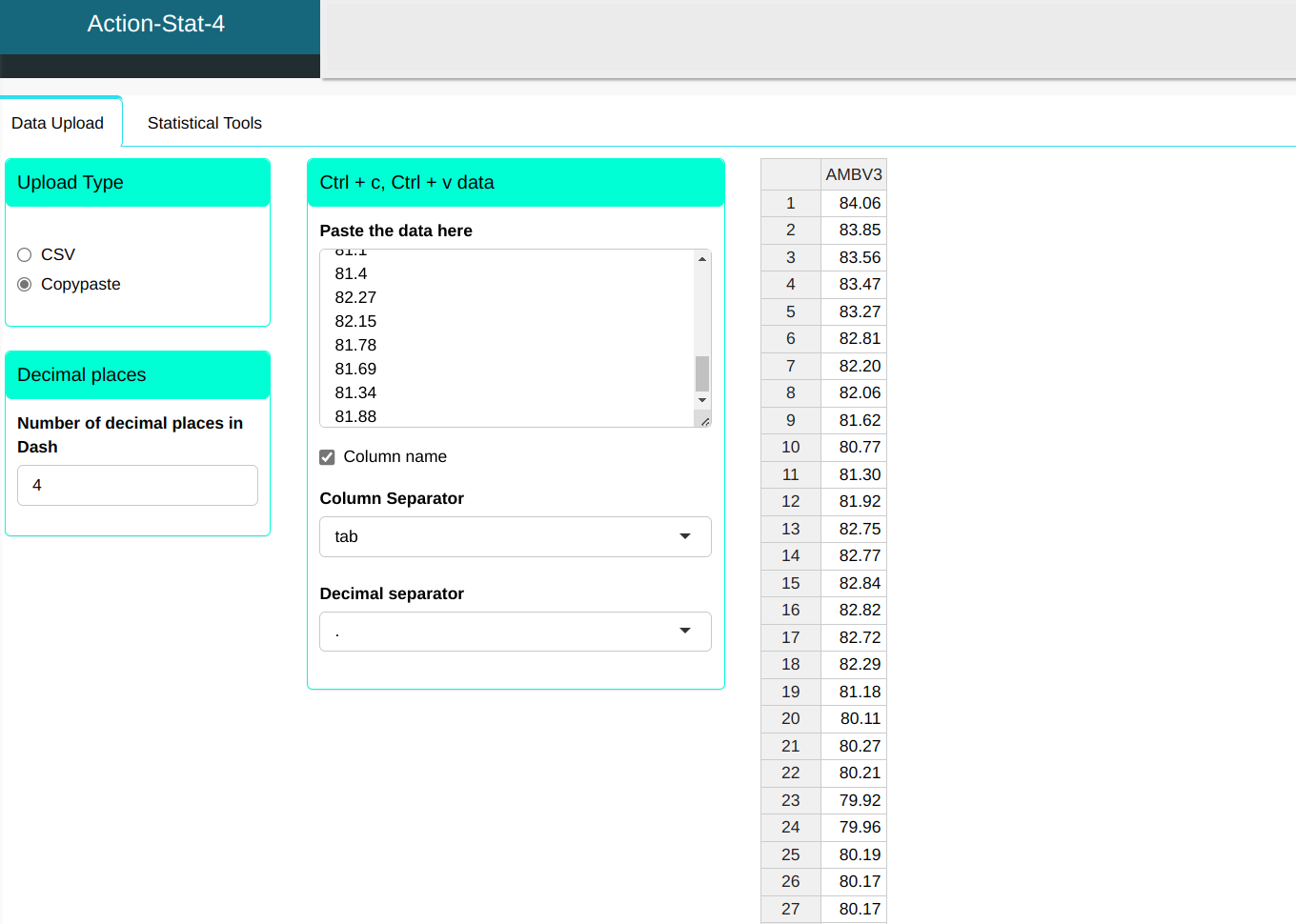
AMBV3
84.06
83.85
83.56
83.47
83.27
82.81
82.20
82.06
81.62
80.77
81.30
81.92
82.75
82.77
82.84
82.82
82.72
82.29
81.18
80.11
80.27
80.21
79.92
79.96
80.19
80.17
80.17
79.85
81.00
80.44
79.96
79.85
79.82
80.11
80.20
80.31
81.18
80.81
81.15
81.32
81.21
81.40
81.10
81.40
82.27
82.15
81.78
81.69
81.34
81.88

---

We will upload the data to the system.

Configuring as shown in the figure below to we will carry out the test.

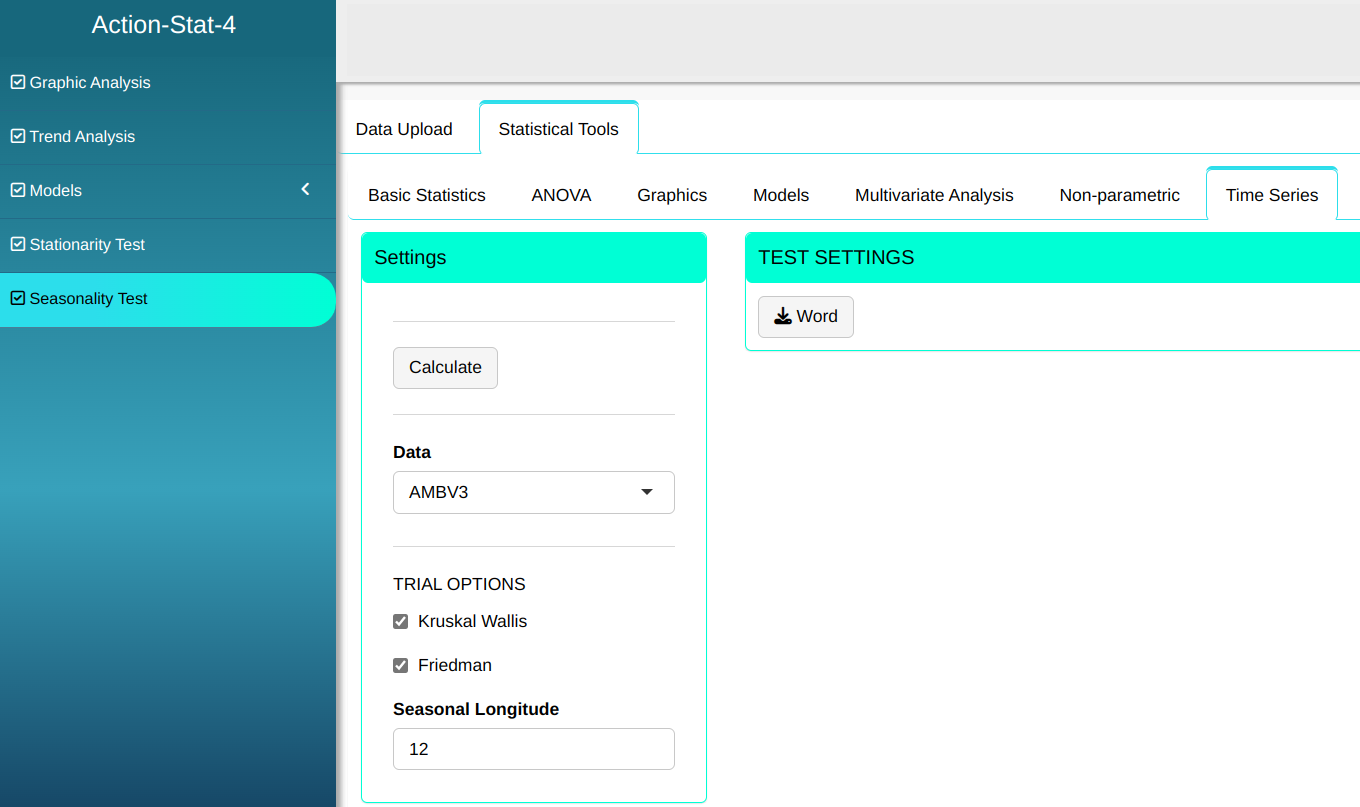
Then click Calculate to get the results. You can also generate the analyses and download them in Word format.

The results are:

Kruskal-Wallis test

	Kruskal-Wallis chi-squared
Statistics	28.0688775510204
P-Value	0.003159616205745
Sample Size	50
Seasonal Length	12
Null Hypothesis	There is no deterministic seasonality
Alternative Hypothesis	There is deterministic seasonality

---

Friedman test

	Friedman chi-squared
Statistics	24.6153846153846
P-Value	0.0103740819044975
Sample Size	50
Seasonal Length	12
Null Hypothesis	There is no deterministic seasonality
Alternative Hypothesis	There is deterministic seasonality

---