2. Confidence Interval
From the confidence interval data it is possible to obtain the size population sample for the mean and proportion.
Example 1:
Suppose that a small pilot sample of n=10, drawn from a population, provided the values $\overline{x}$=15 and $s^2$ =16. What size sample required to estimate the population mean $\mu$ with error sample size and a maximum of 0.5 and with a level of confidence 1- $\alpha$ =0.95.
Then we will calculate the sample size considering the following values
| Standard deviation - s | Significance level | Maximum sample error |
| $\quad\qquad$ 4 | $\quad\qquad$ 0.05 | $\qquad\qquad$0.5 |
To perform the analysis, we configure it as shown in the figure below with the data from the table.


Click Calculate to see the results and download them in Word format.

The results are:
Sample Size Calculation
| tab | |
|---|---|
| Sample Size | 246 |
| Maximum Sample Error | 0.5 |
| Standard Deviation Sampling | 4 |
| Population Size | Info |
| Confidence Level | 0.95 |
From this we conclude that the sample size required to estimate the population mean with a sampling error of at most 0.5 and a 95% confidence level is approximately 246.
Example 2:
Suppose that in a market survey it was estimated that 60% of people respondents prefer to score A for a painkiller. This information is based on previous research. Calculate the sample size so that the sampling error of $\hat{p}$ is smaller than the error of 0.03 and confidence 1- $\alpha$ = 95%.
Then we will calculate the sample size considering the following values
| Sample proportion | Significance level | Maximum sample error |
| $\quad\qquad$ 0.6 | $\quad\qquad$ 0.05 | $\qquad\qquad$0.03 |
To perform the analysis, we configure it as shown in the figure below with the data from the table.

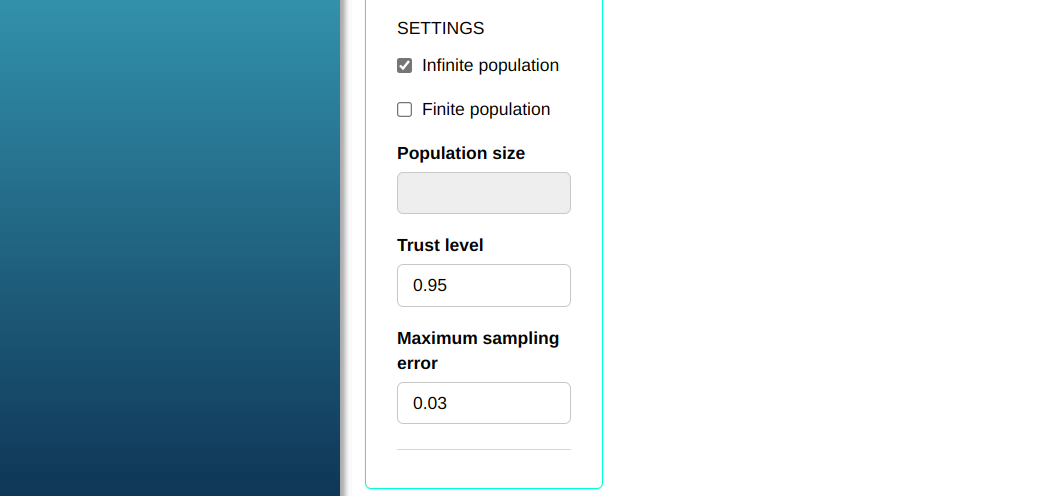
Click Calculate to see the results and download them in Word format.

The results are:
Sample Size Calculation
| tab | |
|---|---|
| Sample Size | 1025 |
| Maximum Sampling Error | 0.03 |
| Sample Proportion | 0.6 |
| Population Size | Info |
| Confidence Level | 0.95 |
With this we conclude that the sample size necessary to estimate the population proportion with a sampling error of at most 0.03 and a level With 95% confidence, it is approximately 1025.