5. Multinomial
Using the Chi-Square test we calculated the power of the hypothesis test or the sample size necessary to have a certain power for the proof.
Example 1:
A manufacturer guarantees that 90% of the parts it supplies to the production line of a given factory conforms to specifications requested. Analysis of a sample of 200 pieces revealed that 25 were defective. At the 5% level, calculate the power of the test to detect the difference between the null proportion of 0.9 and a possible true proportion of 0.8.
We will use the data from the following table.
| n | $\mathbf{p_0}$ | $\mathbf{p_1}$ | $\mathbf{\alpha}$ |
| 200 | (0.9;0,1) | (0.8;0.2) | 0.05 |
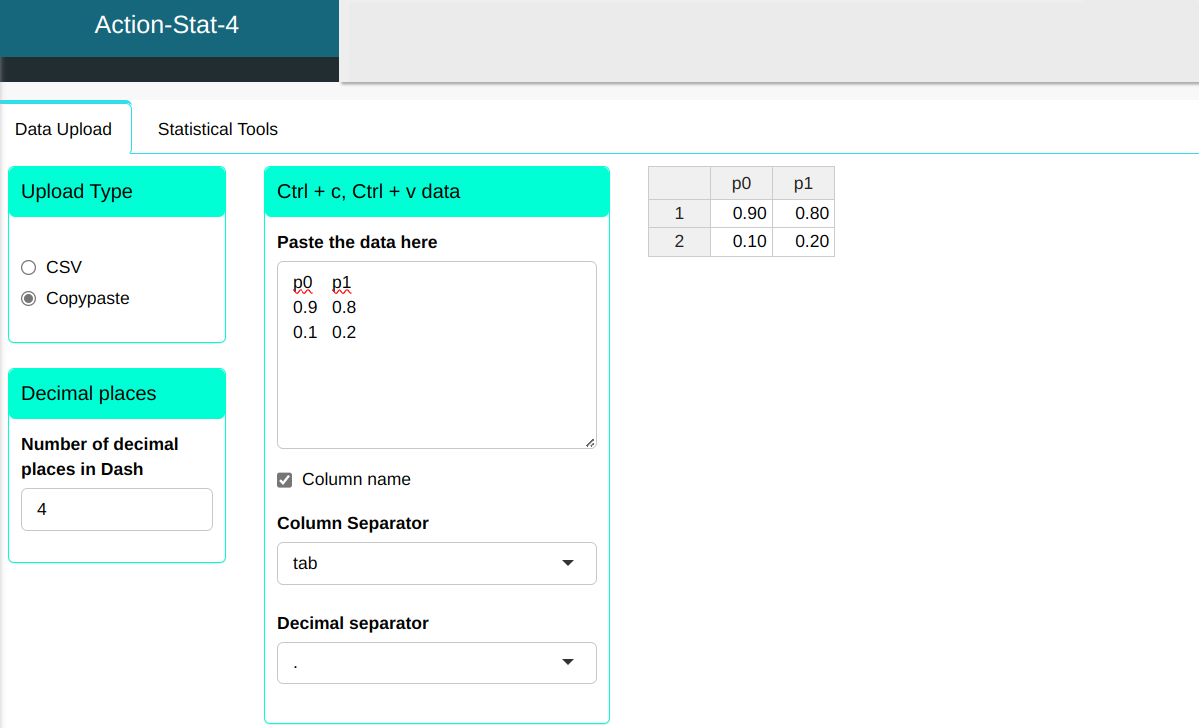
We will upload the data to the system.
| p0 | p1 |
|---|---|
| 0.9 | 0.8 |
| 0.1 | 0.2 |
Configuring as shown in the figure below to calculate the power of the hypothesis test
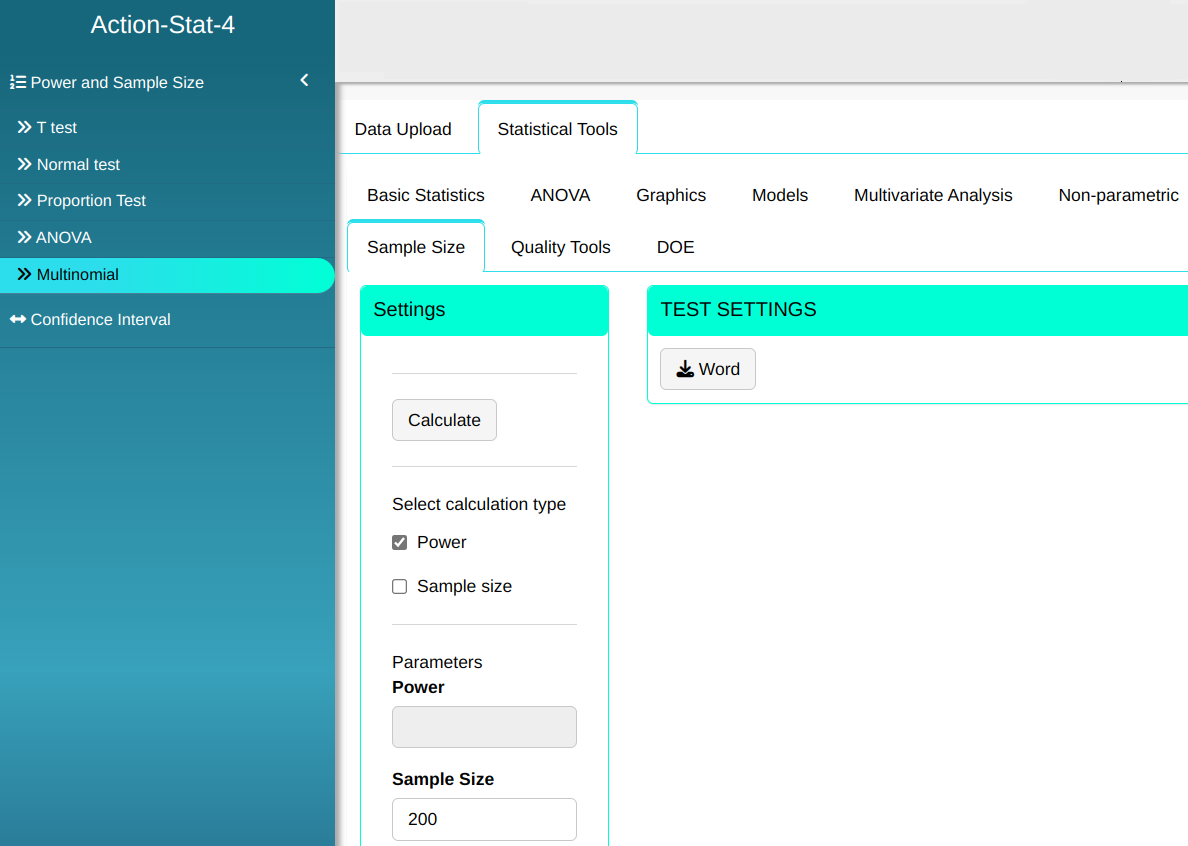

Then click Calculate we obtain the results. You can also generate the analyses and download them in Word format.
The results are:
Analysis result
| Warning | |
| Power | 0.9970571 |
| Sample size | 200 |
| p0 | 0.9 $\quad$ 0.1 |
| p | 0.8 $\quad$ 0.2 |
| Significance level | 0.05 |
With this, we conclude that the power of the test to detect the difference between the null ratio of 0.9 and a possible real ratio of 0.8 is approximately 99.71%.
Example 2:
At the 5% significance level, calculate the required sample size. for the hypothesis test to detect with a power of at least 0.9, a difference between the proportion of the null hypothesis $p_0$ = 0.9 and a possible real proportion p = 0.87.
We will use the data from the following table:
| $\mathbf{p_0}$ | $\mathbf{p_1}$ | $\mathbf{\alpha}$ | Poder |
| (0.9;0,1) | (0.87;0.13) | 0.05 | 0.9 |
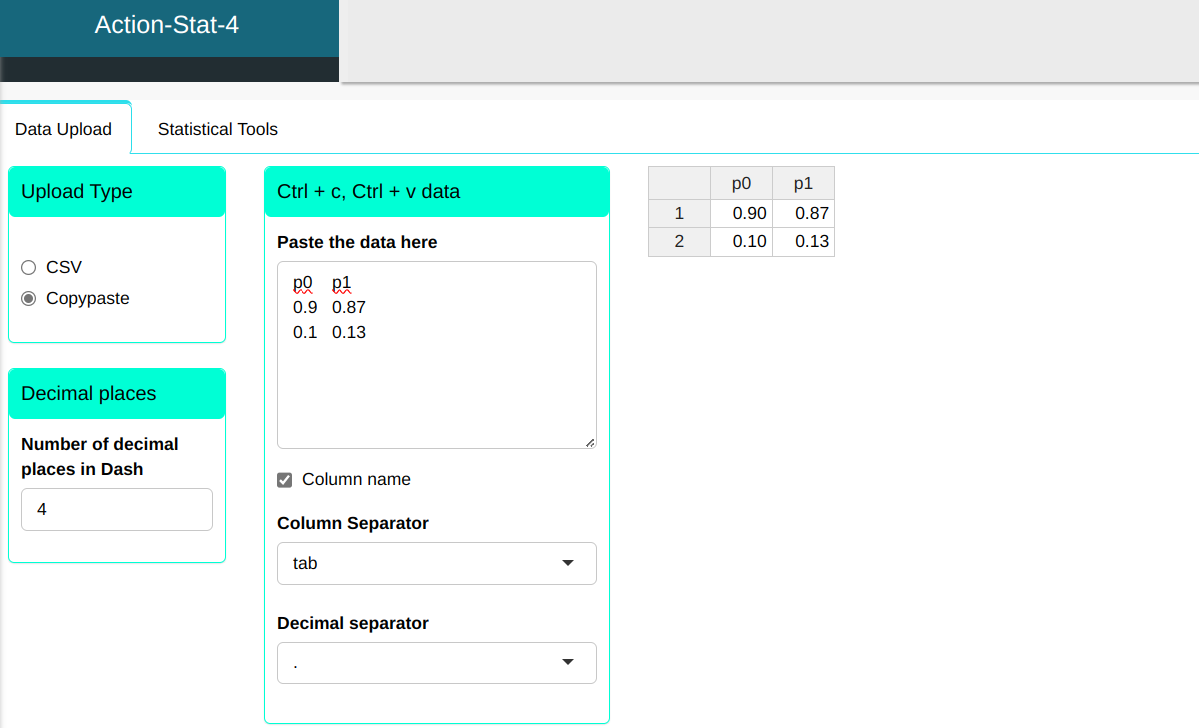
We will upload the data to the system.
| p0 | p1 |
|---|---|
| 0.90 | 0.87 |
| 0.10 | 0.13 |
Configuring as shown in the figure below to calculate the sample size needed
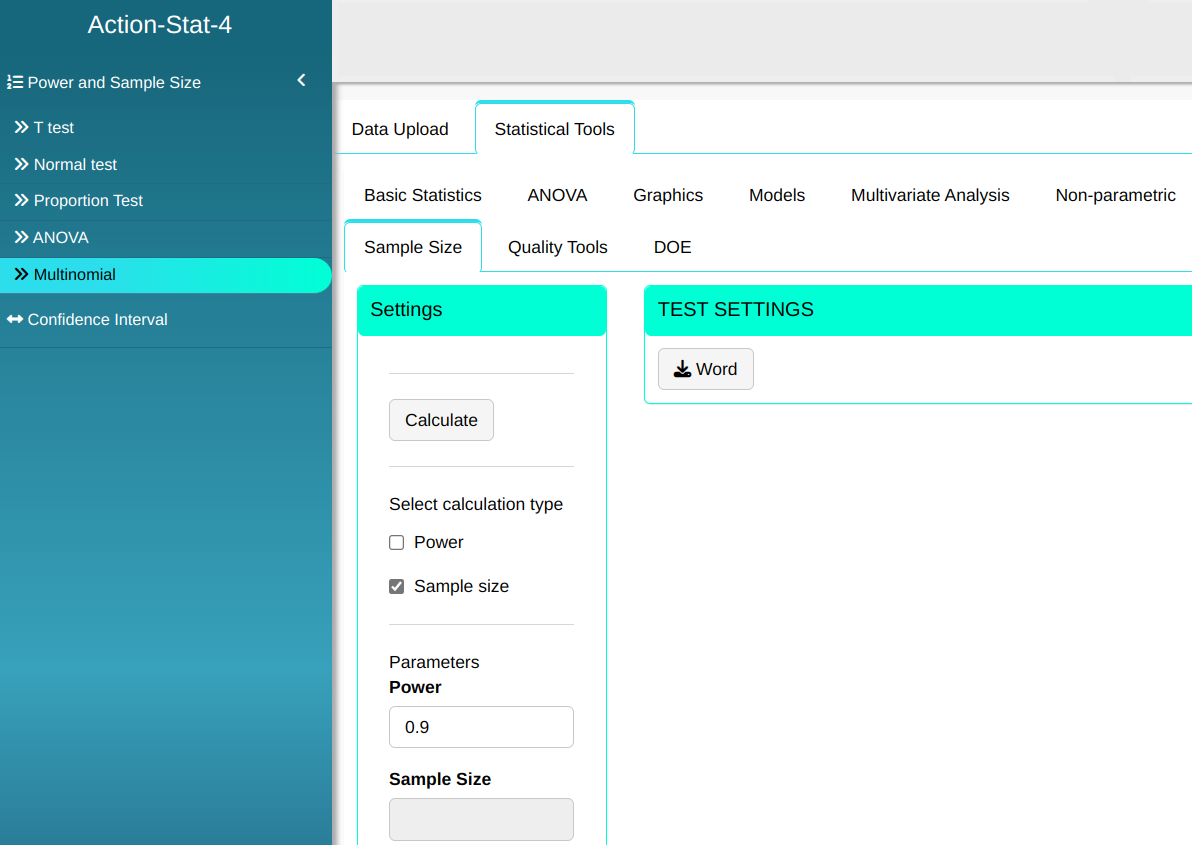

Then click Calculate we obtain the results. You can also generate the analyses and download them in Word format.
The results are:
Analysis result
| Warning | |
| Power | 0.9 |
| Sample size | 1051 |
| Proportion | 0.9 0.1 |
| Hypothetical proportion | 0.87 0.13 |
| Significance level | 0.05 |
We therefore conclude that in order for the test to detect this small difference with a power of at least 0.9, a sample size of at least 1051 is required.