1. Análisis de Conglomerados
El análisis de conglomerados permite agrupar datos según dos tipos de métodos: Jerárquico o K-medias.
Para el método jerárquico, es posible elegir los parámetros de distancia (Euclidiana, Manhattan o Gower) y el método (ward, single, complete, average, median o centroide). Hay opciones para estandarizar los datos, mostrar los datos en un dendrograma y mostrar grupos.
Para el método K-medias solo existe la posibilidad de definir el número de agrupar y estandarizar los datos.
Ejemplo 1:
A un analista financiero le gustaría segmentar las empresas analizadas según los factores que impactan la salud financiera. Un fabricante de bienes de consumo, después de mapear la estructura del mercado y determinar los factores que diferencian los productos, desea segmentarlos. Aplicaremos el Análisis de Cluster utilizando el método de vinculación completa jerárquica utilizando la distancia Euclidiana para comparar grupos.
Los factores mapeados se encuentran en el siguiente cuadro:
| EMPRESA | LC | GA | ROA | SIT |
|---|---|---|---|---|
| AQUATEC | 0.1159 | 0.2673 | -0.2101 | INSOLV |
| BANCO_CREFISUL | 1.0317 | 0.1721 | 0.0196 | INSOLV |
| CASA ANGLO MAPPIN | 2.1758 | 0.0456 | 0.0179 | INSOLV |
| CETENCO | 1.0213 | 0.5076 | 0.0178 | INSOLV |
| CNV CIA VEST | 1.9036 | 1.1809 | -0.0283 | INSOLV |
| COPAS | 0.9484 | 1.3017 | -0.0434 | INSOLV |
| INBRAC | 0.6121 | 0.4972 | -0.3229 | INSOLV |
| MENDES JR | 204 | 0.0667 | 0.0561 | INSOLV |
| MONTREAL | 0.0045 | 0 | -4.1594 | INSOLV |
| PEIXE | 0.2049 | 0 | -0.7039 | INSOLV |
| BRASINCA | 0.1775 | 0.8322 | -0.3944 | INSOLV |
| CIBRAN | 0.4855 | 0.1843 | -0.0048 | INSOLV |
| FERRO LIGAS | 0.6955 | 0.3195 | -0.4052 | INSOLV |
| INDS VER ISHIBRA S | 0.0683 | 0.3828 | -0.0293 | INSOLV |
| LOJAS HERING | 0.6238 | 0.1983 | -0.1372 | INSOLV |
| PARA DE MINAS | 0.2326 | 1014 | -0.4158 | INSOLV |
| TECTOY | 0.9442 | 0.9431 | -0.5884 | INSOLV |
| AIR LIQUIDE | 3.5053 | 0.6109 | -0.0464 | SOLV |
| ANTARCTICA | 0.6613 | 0.3192 | 0.0379 | SOLV |
| ARACRUZ | 1.5707 | 0.1427 | 1 | SOLV |
| ARNO | 2.9656 | 2.0212 | 0.2423 | SOLV |
| ATLAS | 0.9515 | 1.1676 | 0.1214 | SOLV |
| BARDELLA | 2.0071 | 0.2559 | 0.0276 | SOLV |
| BOMPRECO | 0.6804 | 1.6503 | -0.2219 | SOLV |
| BRAHMA | 0.7031 | 0.5195 | 0.0797 | SOLV |
| BRASILIT | 1105 | 0.1958 | 0.2984 | SOLV |
| CACIQUE | 1.1209 | 748 | 0.0464 | SOLV |
| CONFAB TUBOS | 2266 | 0.3392 | 98 | SOLV |
| DURATEX | 2.4744 | 0.4178 | 0.0647 | SOLV |
| EBERLE | 0.4188 | 1.1136 | -0.1495 | SOLV |
| EMBRACO | 1.7798 | 0.7221 | 0.0558 | SOLV |
| ENGEMIX | 1.2954 | 1.2006 | 0.0345 | SOLV |
| ERICSSON | 1.6473 | 629 | 0.1568 | SOLV |
| FICAP | 2.3485 | 1.4813 | 0.1218 | SOLV |
| GERDAU | 1.2619 | 0.3317 | 0.0381 | SOLV |
| LPC DANONE | 1.4377 | 2.3197 | 0.1207 | SOLV |
| MAGNESITA | 1.7495 | 0.7416 | 0.0576 | SOLV |
| MILLENNIUM | 0.9254 | 0.4134 | -0.0289 | SOLV |
| MONARK | 1.9217 | 0.8222 | 0.1926 | SOLV |
| MULTIBRA S | 1.7066 | 1.2666 | 0.2244 | SOLV |
| NADIR FIGUEIREDO | 1.5415 | 826 | 0.0058 | SOLV |
| NITROCARBONO | 0.7424 | 0.9485 | 0.0401 | SOLV |
| PETTENATI | 1.4648 | 0.6864 | 0.2433 | SOLV |
| PIRELLI PNEUS | 1.3069 | 1452 | 0.1059 | SOLV |
| PRONOR PETROQ | 758 | 499 | 0.0472 | SOLV |
| REFINARIA IPIRANGA | 2.5089 | 0.6693 | 0.1258 | SOLV |
| SANTA MARINA | 2.3696 | 0.7963 | 0.1109 | SOLV |
| SP ALPARGATAS | 1.7617 | 1092 | -0.1962 | SOLV |
| YAKULT | 2673 | 1234 | 0.37 | SOLV |
Subiremos los datos al sistema.
Realizaremos análisis de conglomerados. Configuramos conforme la figura de abajo. En este ejemplo dividiremos las empresas en cinco conglomerados.
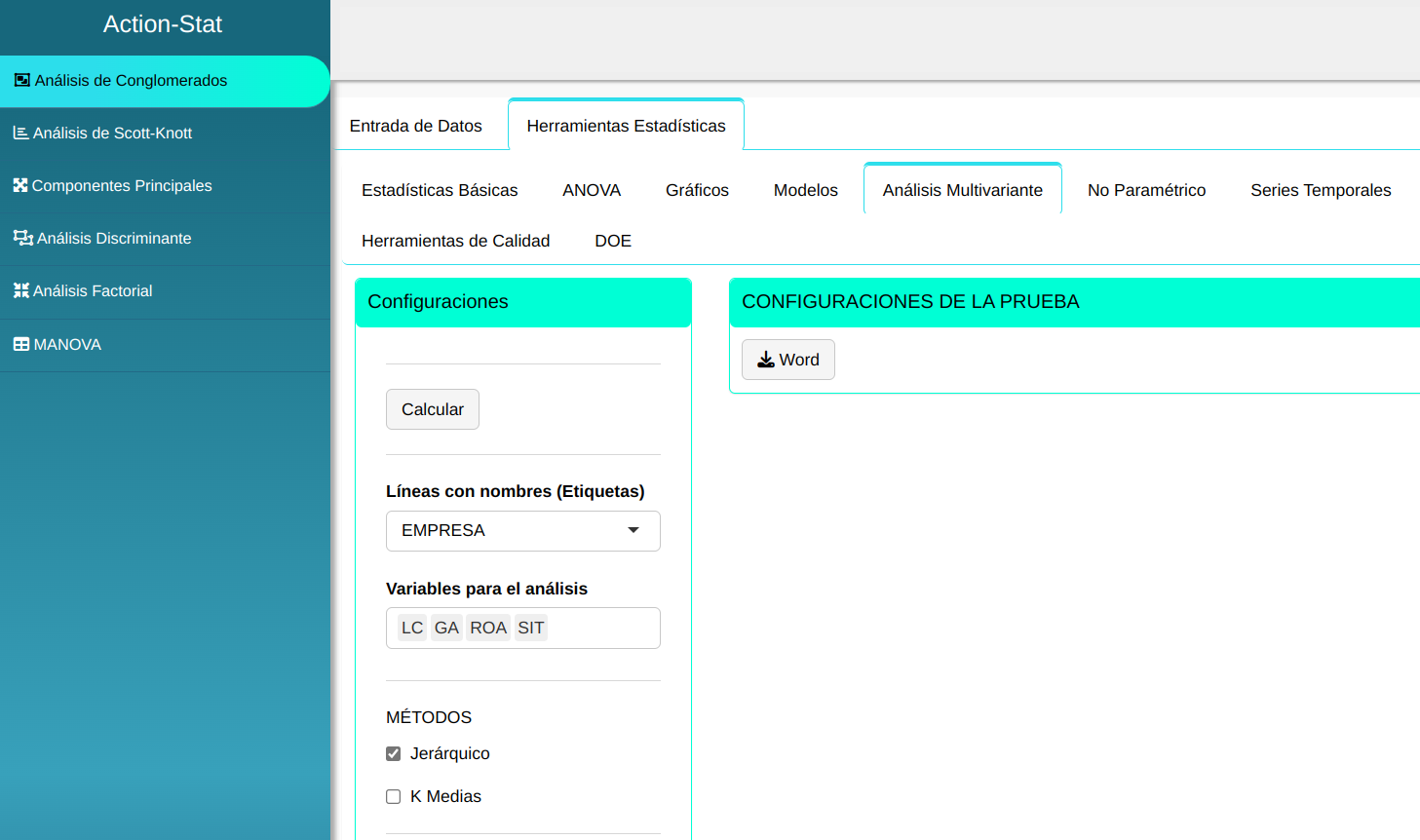
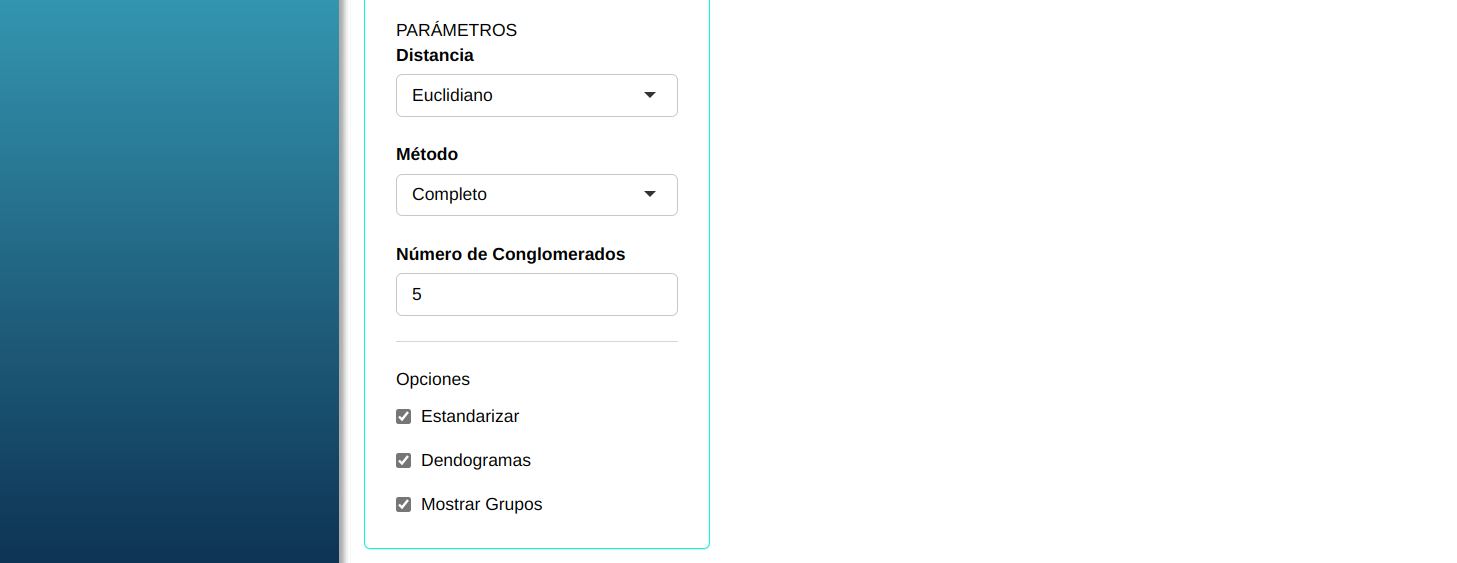
En seguida, haga un clic en calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.

Los resultados son:
Grupo: Método Jerárquico
| Grupo 1 | Grupo 2 | Grupo 3 | Grupo 4 | Grupo 5 |
|---|---|---|---|---|
| AQUATEC | CASA ANGLO (MAPPIN) | MONTREAL | AIRE LIQUIDO | ANTÁRTIDA |
| BANCO_CREFISUL | CNV CIA VEST | ARNO | ARACRUZ | |
| CETENCO | TUBOS CONFAB | ATLAS | ||
| COPAS | DURATEX | BARDELLA | ||
| INBRAC | FICAP | BUENPRECIO | ||
| MENDES JR. | REFINERÍA DE IPIRANGA | BRAHMA | ||
| PESCADO | SANTA MARINA | BRASILIT | ||
| BRASINCÁ | YAKULT | CACIQUE | ||
| CIBRAN | EBERLE | |||
| LIGA DE HIERRO | EMBRACO | |||
| INDS.VER.ISHIBRA´S | ENGEMIX | |||
| TIENDAS HERING | ERICSON | |||
| PARA DEMINAS | GERDAU | |||
| TECTOY | LPC(DANONE) | |||
| MAGNESITA | ||||
| MILLENNIUM | ||||
| MONARK | ||||
| MULTIBRA’S | ||||
| NADIR FIGUEIREDO | ||||
| NITROCARBONO | ||||
| PETTENATI | ||||
| NEUMÁTICOS PIRELLI | ||||
| PRONOR PETROQ. | ||||
| SP ALPARGATAS |
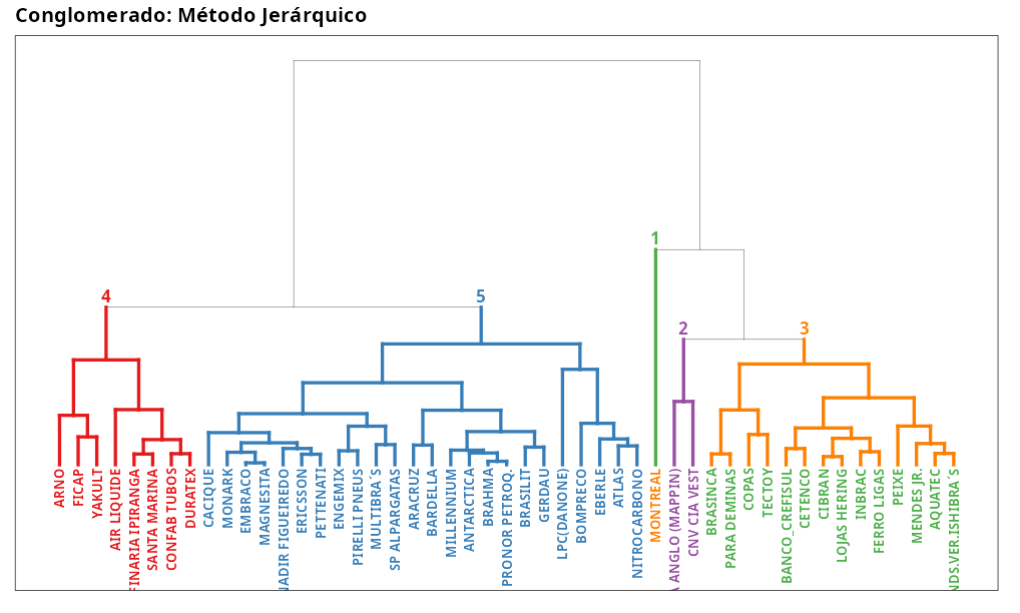
Grupos
| Etiquetas | Orden de etiquetas | Grupos |
|---|---|---|
| AQUATEC | 1 | 1 |
| BANCO_CREFISUL | 2 | 1 |
| CASA ANGLO (MAPPIN) | 3 | 2 |
| CETENCO | 4 | 1 |
| CNV CIA VEST | 5 | 2 |
| COPAS | 6 | 1 |
| INBRAC | 7 | 1 |
| MENDES JR. | 8 | 1 |
| MONTREAL | 9 | 3 |
| PESCADO | 10 | 1 |
| BRASINCÁ | 11 | 1 |
| CIBRAN | 12 | 1 |
| LIGAS DE HIERRO | 13 | 1 |
| INDS.VER.ISHIBRA´S | 14 | 1 |
| TIENDAS HERING | 15 | 1 |
| PARA DEMINAS | 16 | 1 |
| TECTOY | 17 | 1 |
| AIR LIQUIDE | 18 | 4 |
| ANTARCTICA | 19 | 5 |
| ARACRUZ | 20 | 5 |
| ARNO | 21 | 4 |
| ATLAS | 22 | 5 |
| BARDELLA | 23 | 5 |
| BUENPRECIO | 24 | 5 |
| BRAHMA | 25 | 5 |
| BRASILIT | 26 | 5 |
| CACIQUE | 27 | 5 |
| TUBOS CONFAB | 28 | 4 |
| DURATEX | 29 | 4 |
| EBERLE | 30 | 5 |
| EMBRACO | 31 | 5 |
| ENGEMIX | 32 | 5 |
| ERICSSON | 33 | 5 |
| FICAP | 34 | 4 |
| GERDAU | 35 | 5 |
| LPC DANONE | 36 | 5 |
| MAGNESITA | 37 | 5 |
| MILLENNIUM | 38 | 5 |
| MONARK | 39 | 5 |
| MULTIBRA´S | 40 | 5 |
| NADIR FIGUEIREDO | 41 | 5 |
| NITROCARBONO | 42 | 5 |
| PETTENATI | 43 | 5 |
| NEUMÁTICOS PIRELLI | 44 | 5 |
| PRONOR PETROQ. | 45 | 5 |
| REFINERÍA DE IPIRANGA | 46 | 4 |
| SANTA MARINA | 47 | 4 |
| SP ALPARGATAS | 48 | 5 |
| YAKULT | 49 | 4 |
Ejemplo 2:
Considere los ingresos mensuales (en salario mínimo) y la edad de seis personas en una localidad. Aplicaremos el análisis de conglomerados mediante el método jerárquico de vinculación de medias mediante la distancia Euclidiana para comparar los grupos.
| Individuo | Renta | Edad |
|---|---|---|
| A | 9.6 | 28 |
| B | 8.4 | 31 |
| C | 2.4 | 42 |
| D | 18.2 | 38 |
| E | 3.9 | 25 |
| F | 6.4 | 41 |
Subiremos los datos al sistema.
Para realizar el análisis de conglomerados, se realiza la siguiente configuración que se muestra en la figura siguiente.
Al hacer clic en calcular obtenemos los resultados. También se puede descargar el archivo con los resultados en formato Word.

Los resultados son:
Grupo: Método Jerárquico
| Grupo 1 | Grupo 2 |
|---|---|
| A | D |
| B | |
| C | |
| E | |
| F |
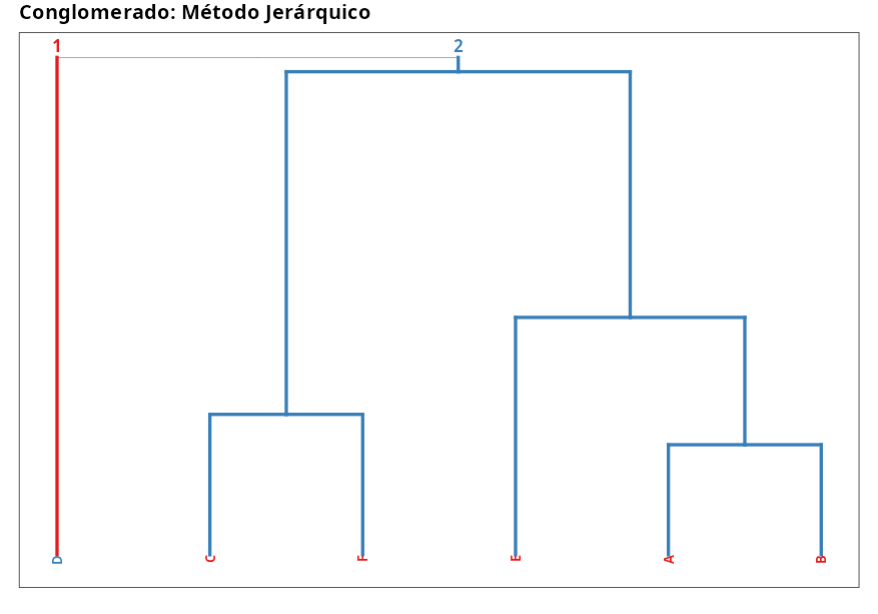
Grupos
| Etiquetas | Orden de etiquetas | Grupos |
|---|---|---|
| A | 1 | 1 |
| B | 2 | 1 |
| C | 3 | 1 |
| D | 4 | 2 |
| E | 5 | 1 |
| F | 6 | 1 |
Ejemplo 3:
Los datos representan, según la base de datos de la ONU (2002), los índices de expectativa de vida, educación, ingresos (PIB) y estabilidad política y seguridad de 21 países. Cuanto mayor sea el valor del índice, mejor será la calidad del país.Se aplicará el análisis de conglomerados mediante el método jerárquico, utilizando la distancia euclidiana y el método de Ward para comparar los grupos.
| Países | Expectativa de Vida | Educación | PIB | Estabilidad Política |
|---|---|---|---|---|
| Reino Unido | 0.88 | 0.99 | 0.91 | 1.1 |
| Austrália | 0.9 | 0.99 | 0.93 | 1.26 |
| Canadá | 0.9 | 0.98 | 0.94 | 1.24 |
| Estados Unidos | 0.87 | 0.98 | 0.97 | 1.18 |
| Japón | 0.93 | 0.93 | 0.93 | 1.2 |
| Francia | 0.89 | 0.97 | 0.92 | 1.04 |
| Singapura | 0.88 | 0.87 | 0.91 | 1.41 |
| Argentina | 0.81 | 0.92 | 0.8 | 0.55 |
| Uruguay | 0.82 | 0.92 | 0.75 | 1.05 |
| Cuba | 0.85 | 0.9 | 0.64 | 0.07 |
| Colômbia | 0.77 | 0.85 | 0.69 | -1.36 |
| Brasil | 0.71 | 0.83 | 0.72 | 0.47 |
| Paraguay | 0.75 | 0.83 | 0.63 | -0.87 |
| Egipto | 0.7 | 0.62 | 0.6 | 0.21 |
| Nigeria | 0.44 | 0.58 | 0.37 | -1.36 |
| Senegal | 0.47 | 0.37 | 0.45 | -0.68 |
| Sierra Leona | 0.23 | 0.33 | 0.27 | -1.26 |
| Angola | 0.34 | 0.36 | 0.51 | -1.98 |
| Etiópia | 0.31 | 0.35 | 0.32 | -0.55 |
| Mozambique | 0.24 | 0.37 | 0.36 | 0.2 |
| China | 0.76 | 0.8 | 0.61 | 0.39 |
Subiremos los datos al sistema:
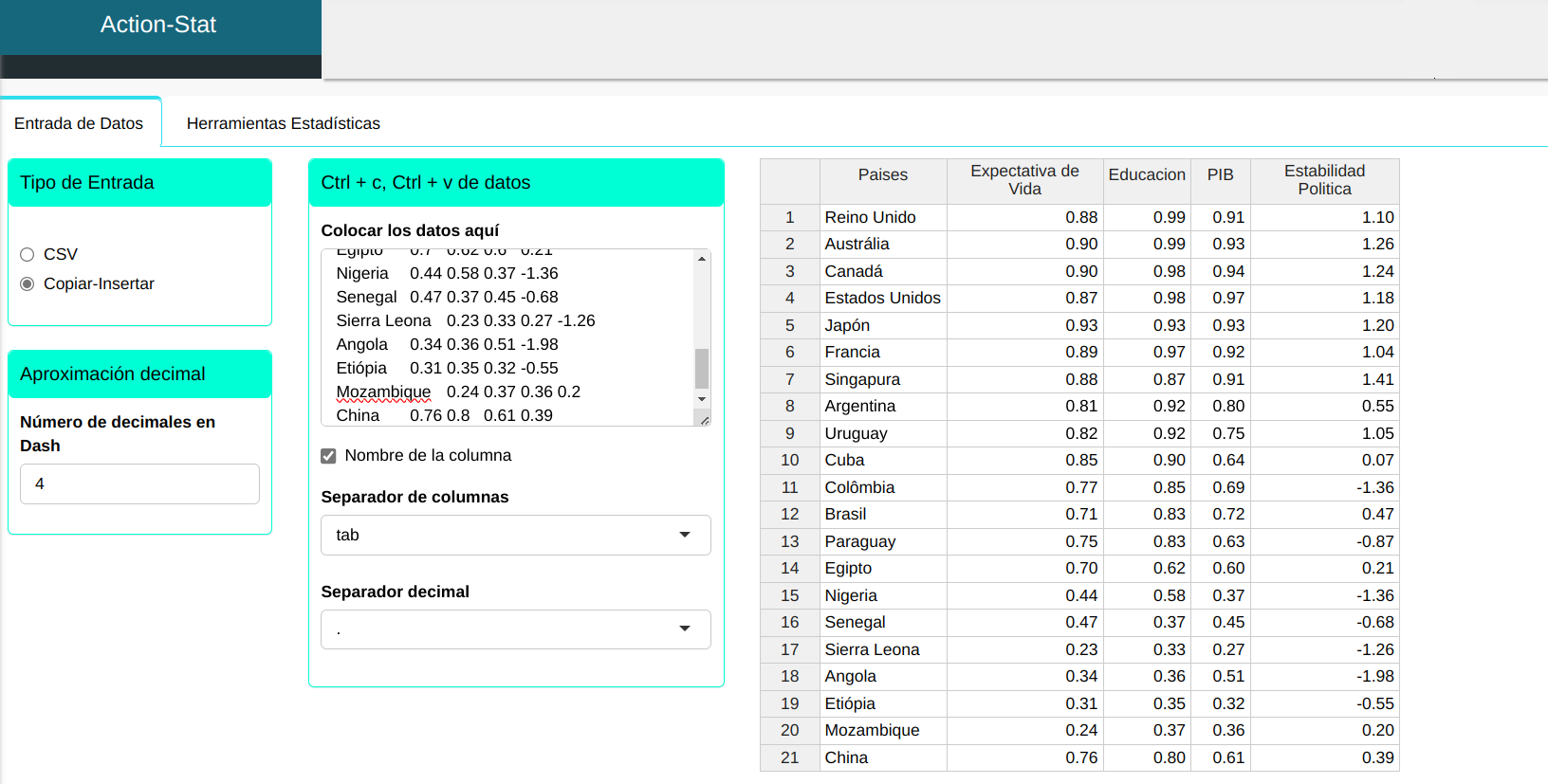
Hagamos un análisis de conglomerados para estos datos. Configuramos conforme la figura de abajo.
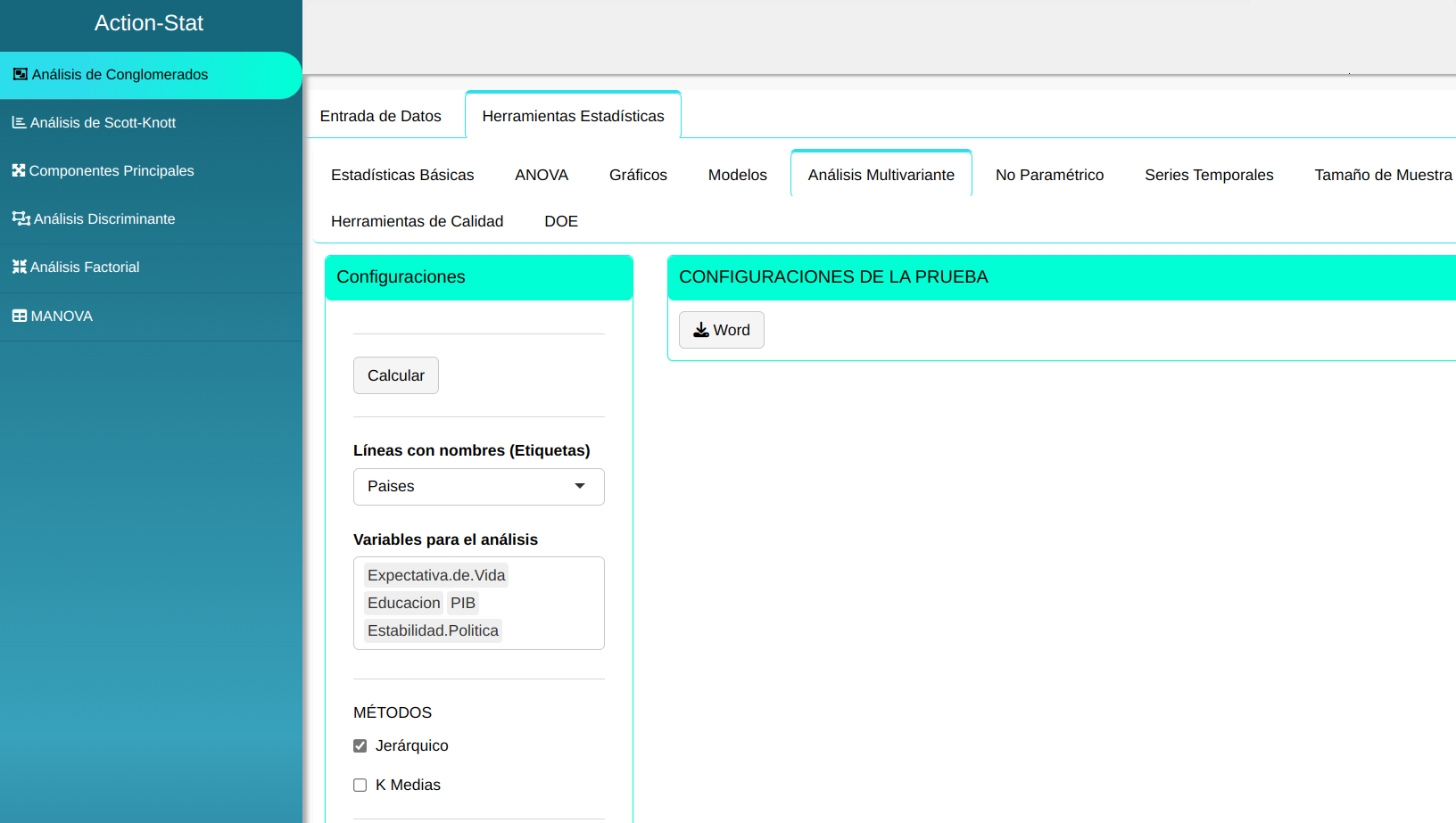
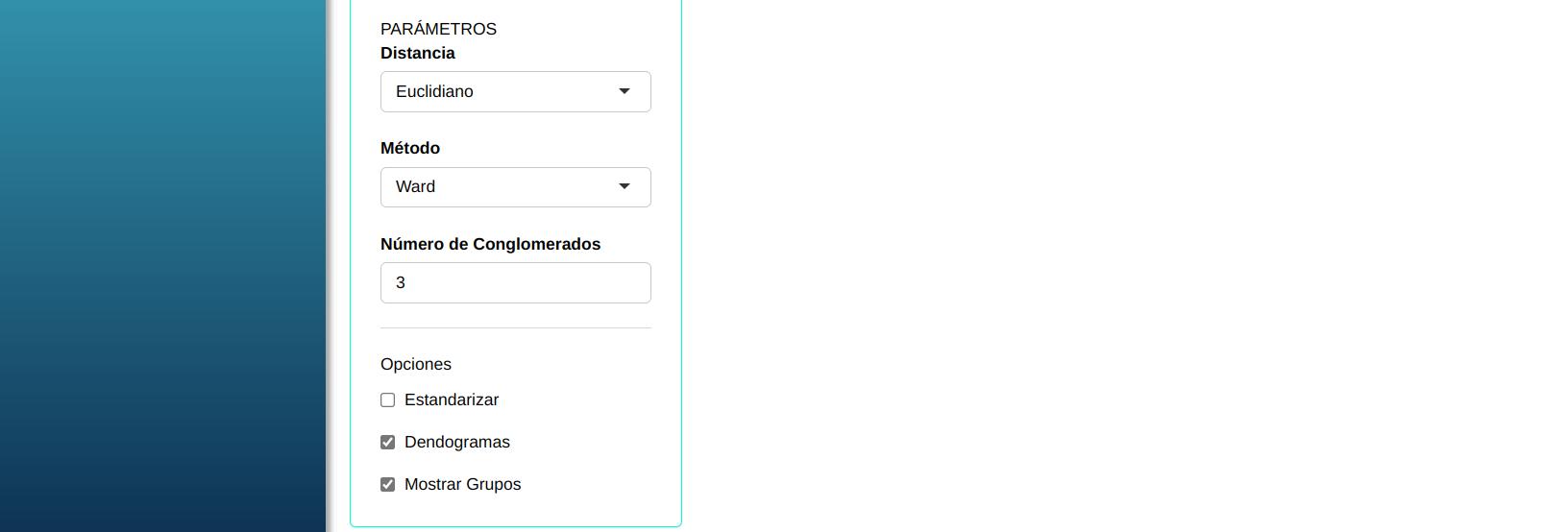
Al hacer clic en Calcular obtenemos los resultados. También se puede descargar el archivo con los resultados en formato Word.

Los resultados son:
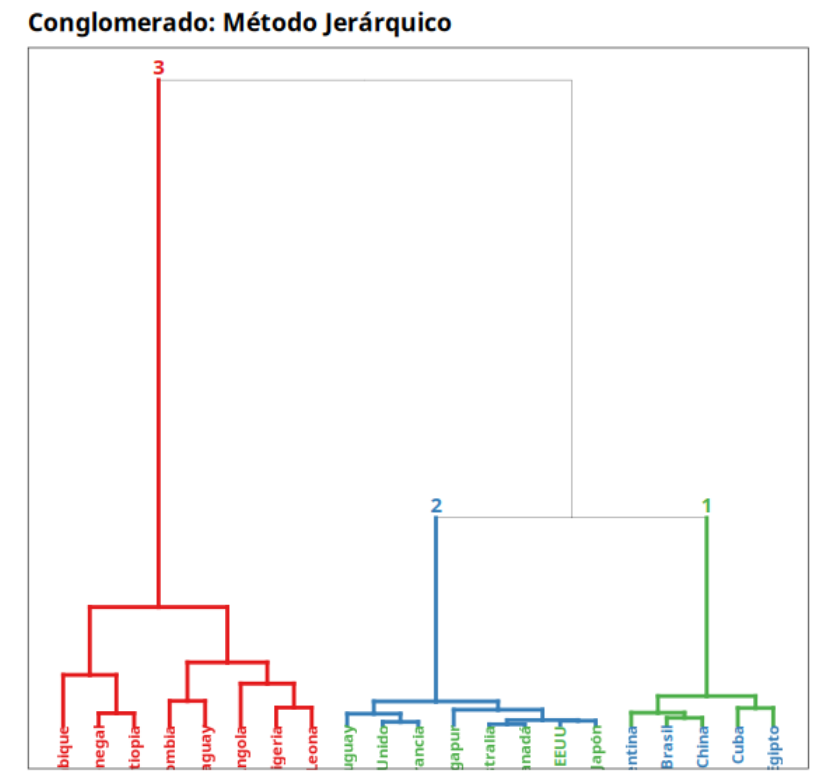
Grupo: Método Jerárquico
| Grupo 1 | Grupo 2 | Grupo 3 |
|---|---|---|
| Reino Unido | Argentina | Colombia |
| Australia | Cuba | Paraguay |
| Canadá | Brasil | Nigeria |
| Estados Unidos | Egipto | Senegal |
| Japón | China | Sierra Leona |
| Francia | Angola | |
| Singapura | Etiópía | |
| Uruguay | Mozambique |
Grupos
| Etiquetas | Orden de etiquetas | Grupos |
|---|---|---|
| Reino Unido | 1 | 1 |
| Australia | 2 | 1 |
| Canadá | 3 | 1 |
| Estados Unidos | 4 | 1 |
| Japón | 5 | 1 |
| Francia | 6 | 1 |
| Singapura | 7 | 1 |
| Argentina | 8 | 2 |
| Uruguay | 9 | 1 |
| Cuba | 10 | 2 |
| Colombia | 11 | 3 |
| Brasil | 12 | 2 |
| Paraguay | 13 | 3 |
| Egipto | 14 | 2 |
| Nigeria | 15 | 3 |
| Senegal | 16 | 3 |
| Sierra Leona | 17 | 3 |
| Angola | 18 | 3 |
| Etiopía | 19 | 3 |
| Mozambique | 20 | 3 |
| China | 21 | 2 |
Ejemplo 4:
El muestreo aleatorio estratificado es común en la recopilación de datos de investigación. La siguiente tabla presenta datos de una encuesta realizada en 120 hogares de una región específica, que mide cinco variables: lugar de residencia, nivel educativo del jefe de hogar, número de personas que viven en el hogar, ingresos familiares mensuales en salarios mínimos e ingresos familiares mensuales per cápita. Utilizaremos el análisis de conglomerados para definir estos estratos, empleando el método jerárquico mediante la distancia de Manhattan y el método de Ward para la comparación de grupos.
| Residencia | Localidad | Nivel Educación | Nro. de residentes | Ingreso Mensual | Ingreso per capita |
|---|---|---|---|---|---|
| 1 | 1 | 3 | 4 | 10.3 | 2.575 |
| 2 | 1 | 3 | 4 | 15.4 | 3.850 |
| 3 | 1 | 2 | 4 | 9.6 | 2.400 |
| 4 | 1 | 2 | 5 | 5.5 | 1.100 |
| 5 | 1 | 3 | 4 | 9 | 2.250 |
| 6 | 1 | 1 | 1 | 2.4 | 2.400 |
| 7 | 1 | 3 | 2 | 4.1 | 2.050 |
| 8 | 1 | 3 | 3 | 8.4 | 2.800 |
| 9 | 1 | 3 | 6 | 10.3 | 1.717 |
| 10 | 1 | 2 | 4 | 4.6 | 1.150 |
| 11 | 1 | 2 | 6 | 18.6 | 3.100 |
| 12 | 1 | 1 | 4 | 7.1 | 1.775 |
| 13 | 1 | 2 | 4 | 12.9 | 3.225 |
| 14 | 1 | 2 | 6 | 8.4 | 1.400 |
| 15 | 1 | 3 | 3 | 19.3 | 6.433 |
| 16 | 1 | 2 | 5 | 10.4 | 2.080 |
| 17 | 1 | 3 | 3 | 8.9 | 2.967 |
| 18 | 1 | 3 | 4 | 12.9 | 3.225 |
| 19 | 1 | 3 | 4 | 5.1 | 1.275 |
| 20 | 1 | 3 | 4 | 12.2 | 3.050 |
| 21 | 1 | 3 | 5 | 5.8 | 1.160 |
| 22 | 1 | 3 | 5 | 12.9 | 2.580 |
| 23 | 1 | 3 | 5 | 7.7 | 1.540 |
| 24 | 1 | 2 | 4 | 1.1 | 0.275 |
| 25 | 1 | 2 | 8 | 7.5 | 0.938 |
| 26 | 1 | 3 | 4 | 5.8 | 1.450 |
| 27 | 1 | 1 | 5 | 7.2 | 1.440 |
| 28 | 1 | 3 | 3 | 8.6 | 2.867 |
| 29 | 1 | 2 | 4 | 5.1 | 1.275 |
| 30 | 1 | 3 | 5 | 2.6 | 0.520 |
| 31 | 1 | 3 | 5 | 7.7 | 1.540 |
| 32 | 1 | 2 | 2 | 2.4 | 1.200 |
| 33 | 1 | 3 | 5 | 4.8 | 0.960 |
| 34 | 1 | 1 | 2 | 2.1 | 1.050 |
| 35 | 1 | 1 | 6 | 4 | 0.667 |
| 36 | 1 | 1 | 8 | 12.5 | 1.563 |
| 37 | 1 | 3 | 3 | 6.8 | 2.267 |
| 38 | 1 | 3 | 5 | 3.9 | 0.780 |
| 39 | 1 | 3 | 5 | 9 | 1.800 |
| 40 | 1 | 3 | 3 | 10.9 | 3.633 |
| 41 | 2 | 2 | 5 | 5.4 | 1.080 |
| 42 | 2 | 1 | 3 | 6.4 | 2.133 |
| 43 | 2 | 1 | 6 | 4.4 | 0.733 |
| 44 | 2 | 1 | 5 | 2.5 | 0.500 |
| 45 | 2 | 1 | 6 | 5.5 | 0.917 |
| 46 | 2 | 1 | 8 | 4.8 | 0.600 |
| 47 | 2 | 3 | 4 | 14 | 3.500 |
| 48 | 2 | 2 | 4 | 8.5 | 2.125 |
| 49 | 2 | 1 | 5 | 7.7 | 1.540 |
| 50 | 2 | 2 | 3 | 5.8 | 1.933 |
| 51 | 2 | 3 | 5 | 5 | 1.000 |
| 52 | 2 | 1 | 3 | 4.8 | 1.600 |
| 53 | 2 | 2 | 2 | 2.8 | 1.400 |
| 54 | 2 | 2 | 4 | 4.2 | 1.050 |
| 55 | 2 | 3 | 3 | 10.2 | 3.400 |
| 56 | 2 | 2 | 4 | 7.4 | 1.850 |
| 57 | 2 | 2 | 5 | 5 | 1.000 |
| 58 | 2 | 3 | 2 | 6.4 | 3.200 |
| 59 | 2 | 3 | 4 | 5.7 | 1.425 |
| 60 | 2 | 2 | 4 | 10.8 | 2.700 |
| 61 | 2 | 3 | 1 | 2.3 | 2.300 |
| 62 | 2 | 1 | 7 | 6.1 | 0.871 |
| 63 | 2 | 1 | 3 | 5.5 | 1.833 |
| 64 | 2 | 1 | 7 | 3.5 | 0.500 |
| 65 | 2 | 3 | 3 | 9 | 3.000 |
| 66 | 2 | 3 | 6 | 5.8 | 0.967 |
| 67 | 2 | 1 | 6 | 4.2 | 0.700 |
| 68 | 2 | 3 | 3 | 6.8 | 2.267 |
| 69 | 2 | 2 | 5 | 4.8 | 0.960 |
| 70 | 2 | 3 | 5 | 6 | 1.200 |
| 71 | 2 | 2 | 7 | 9 | 1.286 |
| 72 | 2 | 1 | 4 | 5.3 | 1.325 |
| 73 | 2 | 3 | 4 | 3.1 | 0.775 |
| 74 | 2 | 3 | 1 | 6.4 | 6.400 |
| 75 | 2 | 1 | 3 | 3.9 | 1.300 |
| 76 | 2 | 2 | 3 | 6.4 | 2.133 |
| 77 | 2 | 3 | 4 | 2.7 | 0.675 |
| 78 | 2 | 2 | 4 | 2.4 | 0.600 |
| 79 | 2 | 2 | 4 | 3.6 | 0.900 |
| 80 | 2 | 3 | 5 | 6.4 | 1.280 |
| 81 | 2 | 3 | 2 | 11.3 | 5.650 |
| 82 | 2 | 1 | 5 | 3.8 | 0.760 |
| 83 | 2 | 2 | 3 | 4.1 | 1.367 |
| 84 | 3 | 1 | 5 | 1.8 | 0.360 |
| 85 | 3 | 3 | 5 | 7.1 | 1.420 |
| 86 | 3 | 1 | 3 | 13.9 | 4.633 |
| 87 | 3 | 2 | 6 | 4 | 0.667 |
| 88 | 3 | 1 | 6 | 2.9 | 0.483 |
| 89 | 3 | 2 | 9 | 3.9 | 0.433 |
| 90 | 3 | 1 | 4 | 2.2 | 0.550 |
| 91 | 3 | 2 | 3 | 5.8 | 1.933 |
| 92 | 3 | 2 | 5 | 2.8 | 0.560 |
| 93 | 3 | 2 | 5 | 4.5 | 0.900 |
| 94 | 3 | 2 | 4 | 5.8 | 1.450 |
| 95 | 3 | 3 | 8 | 3.9 | 0.488 |
| 96 | 3 | 2 | 7 | 2.8 | 0.400 |
| 97 | 3 | 1 | 3 | 1.3 | 0.433 |
| 98 | 3 | 3 | 5 | 3.9 | 0.780 |
| 99 | 3 | 3 | 5 | 5 | 1.000 |
| 100 | 3 | 1 | 5 | 0.1 | 0.020 |
| 101 | 3 | 2 | 3 | 4.6 | 1.533 |
| 102 | 3 | 2 | 4 | 2.6 | 0.650 |
| 103 | 3 | 1 | 6 | 2.3 | 0.383 |
| 104 | 3 | 2 | 5 | 4.9 | 0.980 |
| 105 | 3 | 1 | 5 | 2.3 | 0.460 |
| 106 | 3 | 1 | 3 | 3.9 | 1.300 |
| 107 | 3 | 1 | 4 | 2.1 | 0.525 |
| 108 | 3 | 1 | 4 | 2.7 | 0.675 |
| 109 | 3 | 2 | 5 | 11.1 | 2.220 |
| 110 | 3 | 1 | 6 | 6.4 | 1.067 |
| 111 | 3 | 3 | 7 | 25.7 | 3.671 |
| 112 | 3 | 1 | 4 | 0.9 | 0.225 |
| 113 | 3 | 3 | 5 | 3.9 | 0.780 |
| 114 | 3 | 1 | 5 | 5.1 | 1.020 |
| 115 | 3 | 2 | 6 | 4.2 | 0.700 |
| 116 | 3 | 1 | 6 | 4.4 | 0.733 |
| 117 | 3 | 1 | 7 | 7.9 | 1.129 |
| 118 | 3 | 1 | 4 | 4.2 | 1.050 |
| 119 | 3 | 1 | 4 | 3.5 | 0.875 |
| 120 | 3 | 2 | 6 | 11.4 | 1.900 |
Haremos el upload de los datos en el sistema.
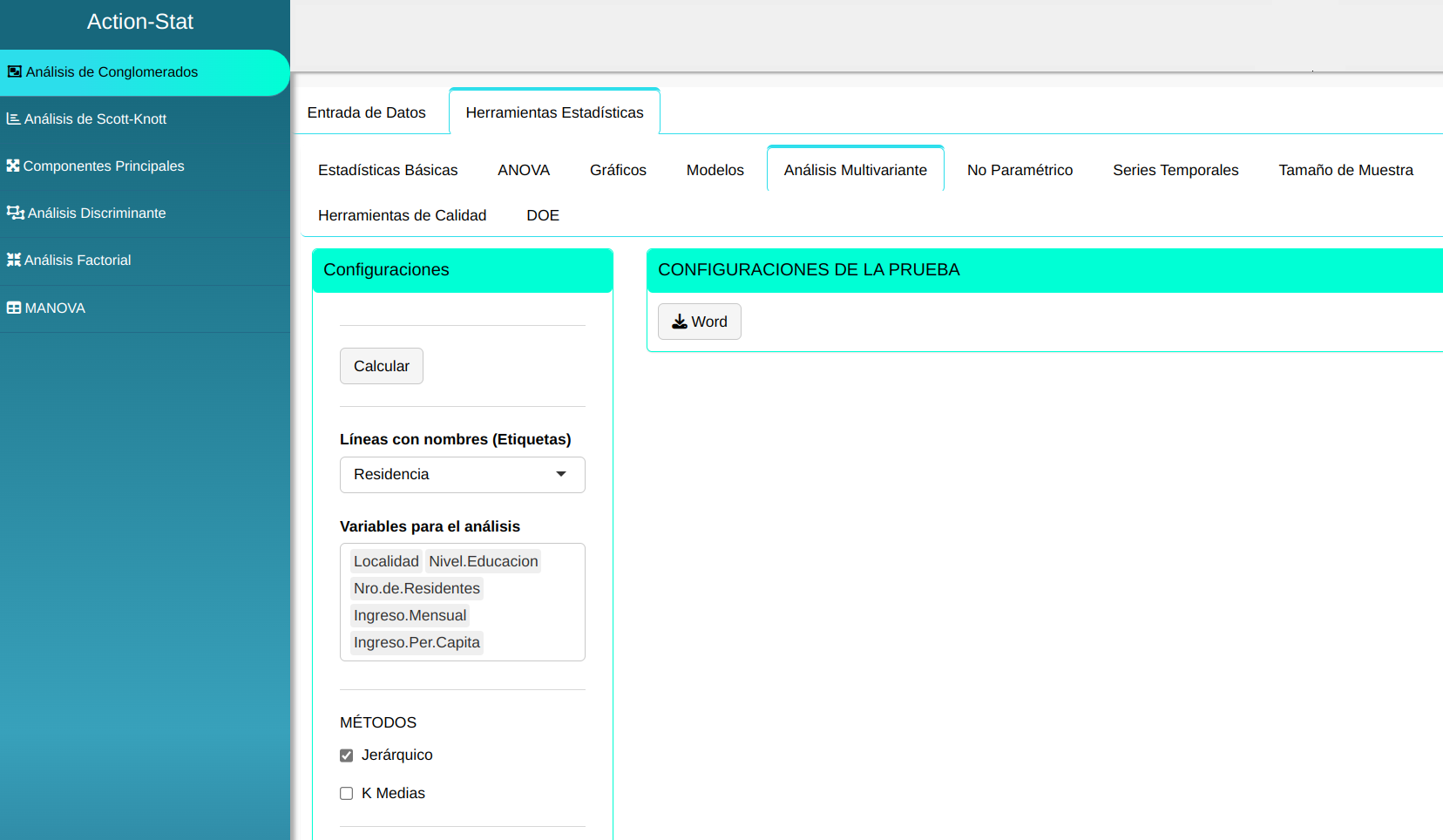
Haremos el análisis de conglomerados, configurando conforme la figura de abajo.
Al hacer clic en Calcular obtenemos los resultados. También se puede descargar el archivo con los resultados en formato word.

Los resultados son:
Grupos: Método Jerárquico
| Grupo 1 | Grupo 2 | Grupo 3 | Grupo 4 | Grupo 5 | Grupo 6 |
|---|---|---|---|---|---|
| 1 | 2 | 4 | 6 | 24 | 35 |
| 3 | 11 | 10 | 7 | 44 | 43 |
| 5 | 13 | 19 | 32 | 73 | 45 |
| 8 | 15 | 21 | 34 | 77 | 46 |
| 9 | 18 | 26 | 37 | 78 | 62 |
| 12 | 20 | 29 | 42 | 82 | 64 |
| 14 | 22 | 30 | 50 | 84 | 67 |
| 16 | 47 | 33 | 52 | 88 | 87 |
| 17 | 86 | 38 | 53 | 90 | 89 |
| 23 | 111 | 41 | 58 | 92 | 95 |
| 25 | 51 | 61 | 97 | 96 | |
| 27 | 54 | 63 | 100 | 110 | |
| 28 | 57 | 68 | 102 | 115 | |
| 31 | 59 | 72 | 103 | 116 | |
| 36 | 66 | 75 | 105 | 117 | |
| 39 | 69 | 76 | 107 | ||
| 40 | 70 | 83 | 108 | ||
| 48 | 79 | 91 | 112 | ||
| 49 | 80 | 94 | 118 | ||
| 55 | 85 | 101 | 119 | ||
| 56 | 93 | 106 | |||
| 60 | 98 | ||||
| 65 | 99 | ||||
| 71 | 104 | ||||
| 74 | 113 | ||||
| 81 | 114 | ||||
| 109 | |||||
| 120 |
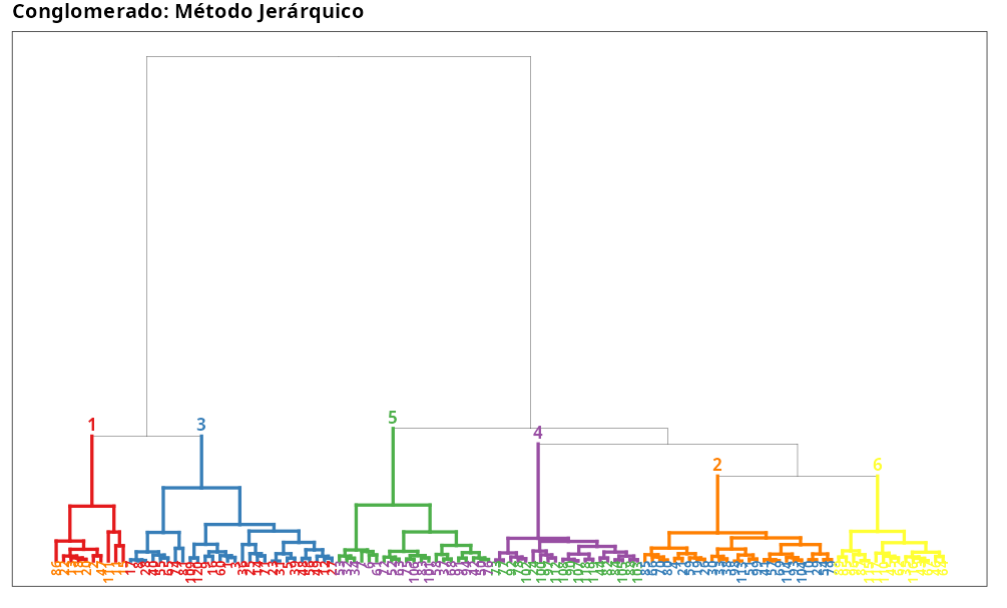
Grupos
| Etiquetas | Orden de las etiquetas | Grupos |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 3 | 1 |
| 4 | 4 | 3 |
| 5 | 5 | 1 |
| 6 | 6 | 4 |
| 7 | 7 | 4 |
| 8 | 8 | 1 |
| 9 | 9 | 1 |
| 10 | 10 | 3 |
| 11 | 11 | 2 |
| 12 | 12 | 1 |
| 13 | 13 | 2 |
| 14 | 14 | 1 |
| 15 | 15 | 2 |
| 16 | 16 | 1 |
| 17 | 17 | 1 |
| 18 | 18 | 2 |
| 19 | 19 | 3 |
| 20 | 20 | 2 |
| 21 | 21 | 3 |
| 22 | 22 | 2 |
| 23 | 23 | 1 |
| 24 | 24 | 5 |
| 25 | 25 | 1 |
| 26 | 26 | 3 |
| 27 | 27 | 1 |
| 28 | 28 | 1 |
| 29 | 29 | 3 |
| 30 | 30 | 3 |
| 31 | 31 | 1 |
| 32 | 32 | 4 |
| 33 | 33 | 3 |
| 34 | 34 | 4 |
| 35 | 35 | 6 |
| 36 | 36 | 1 |
| 37 | 37 | 4 |
| 38 | 38 | 3 |
| 39 | 39 | 1 |
| 40 | 40 | 1 |
| 41 | 41 | 3 |
| 42 | 42 | 4 |
| 43 | 43 | 6 |
| 44 | 44 | 5 |
| 45 | 45 | 6 |
| 46 | 46 | 6 |
| 47 | 47 | 2 |
| 48 | 48 | 1 |
| 49 | 49 | 1 |
| 50 | 50 | 4 |
| 51 | 51 | 3 |
| 52 | 52 | 4 |
| 53 | 53 | 4 |
| 54 | 54 | 3 |
| 55 | 55 | 1 |
| 56 | 56 | 1 |
| 57 | 57 | 3 |
| 58 | 58 | 4 |
| 59 | 59 | 3 |
| 60 | 60 | 1 |
| 61 | 61 | 4 |
| 62 | 62 | 6 |
| 63 | 63 | 4 |
| 64 | 64 | 6 |
| 65 | 65 | 1 |
| 66 | 66 | 3 |
| 67 | 67 | 6 |
| 68 | 68 | 4 |
| 69 | 69 | 3 |
| 70 | 70 | 3 |
| 71 | 71 | 1 |
| 72 | 72 | 4 |
| 73 | 73 | 5 |
| 74 | 74 | 1 |
| 75 | 75 | 4 |
| 76 | 76 | 4 |
| 77 | 77 | 5 |
| 78 | 78 | 5 |
| 79 | 79 | 3 |
| 80 | 80 | 3 |
| 81 | 81 | 1 |
| 82 | 82 | 5 |
| 83 | 83 | 4 |
| 84 | 84 | 5 |
| 85 | 85 | 3 |
| 86 | 86 | 2 |
| 87 | 87 | 6 |
| 88 | 88 | 5 |
| 89 | 89 | 6 |
| 90 | 90 | 5 |
| 91 | 91 | 4 |
| 92 | 92 | 5 |
| 93 | 93 | 3 |
| 94 | 94 | 4 |
| 95 | 95 | 6 |
| 96 | 96 | 6 |
| 97 | 97 | 5 |
| 98 | 98 | 3 |
| 99 | 99 | 3 |
| 100 | 100 | 5 |
| 101 | 101 | 4 |
| 102 | 102 | 5 |
| 103 | 103 | 5 |
| 104 | 104 | 3 |
| 105 | 105 | 5 |
| 106 | 106 | 4 |
| 107 | 107 | 5 |
| 108 | 108 | 5 |
| 109 | 109 | 1 |
| 110 | 110 | 6 |
| 111 | 111 | 2 |
| 112 | 112 | 5 |
| 113 | 113 | 3 |
| 114 | 114 | 3 |
| 115 | 115 | 6 |
| 116 | 116 | 6 |
| 117 | 117 | 6 |
| 118 | 118 | 5 |
| 119 | 119 | 5 |
| 120 | 120 | 1 |
Ejemplo 5:
Una cervecería quiere estudiar los gustos de sus clientes en relación a algunas marcas de cerveza. El siguiente cuadro representa los resultados de un estudio de las percepciones y preferencias. Cada estudiante calificó las 10 marcas de cerveza en una escala de 10 puntos: Anchor Steam, Bass Ale, Beck's, Corona, Gordo-Biersch, Guinness, Heineken, Pete's Wicked Ale, Sam Adams y Sierra Nevada. Aplicaremos Análisis de Cluster utilizando el método K-means para comparar grupos.
| Obs. | Anchor Steam | Bass Ale | Beck's | Corona | Gordo-Biersch | Guinness | Heineken | Pete's Wicked Ale | Sam Adams | Sierra Nevada |
|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 5 | 9 | 7 | 1 | 7 | 6 | 6 | 5 | 9 | 5 |
| P2 | 7 | 5 | 6 | 8 | 8 | 4 | 8 | 8 | 7 | 7 |
| P3 | 7 | 7 | 5 | 6 | 6 | 1 | 8 | 4 | 7 | 5 |
| P4 | 7 | 7 | 5 | 2 | 5 | 8 | 4 | 6 | 8 | 9 |
| P5 | 9 | 7 | 3 | 1 | 6 | 8 | 2 | 7 | 6 | 8 |
| P6 | 7 | 6 | 4 | 3 | 7 | 6 | 6 | 5 | 4 | 9 |
| P7 | 5 | 5 | 5 | 6 | 6 | 4 | 7 | 5 | 5 | 6 |
| P8 | 5 | 3 | 1 | 5 | 5 | 5 | 3 | 5 | 5 | 9 |
| P9 | 9 | 3 | 2 | 6 | 4 | 6 | 1 | 5 | 3 | 6 |
| P10 | 2 | 6 | 6 | 5 | 6 | 4 | 8 | 4 | 4 | 3 |
| P11 | 7 | 7 | 7 | 5 | 7 | 8 | 6 | 7 | 7 | 8 |
| P12 | 8 | 3 | 3 | 9 | 9 | 2 | 1 | 9 | 7 | 8 |
| P13 | 6 | 5 | 3 | 7 | 6 | 5 | 8 | 6 | 7 | 5 |
| P14 | 5 | 6 | 3 | 8 | 6 | 7 | 6 | 7 | 6 | 7 |
| P15 | 4 | 7 | 2 | 8 | 5 | 9 | 8 | 3 | 8 | 8 |
| P16 | 3 | 3 | 4 | 5 | 6 | 5 | 9 | 7 | 5 | 5 |
| P17 | 2 | 5 | 5 | 7 | 6 | 6 | 8 | 1 | 7 | 4 |
| P18 | 9 | 3 | 7 | 4 | 2 | 4 | 6 | 3 | 8 | 6 |
| P19 | 5 | 3 | 4 | 7 | 7 | 7 | 6 | 6 | 6 | 6 |
| P20 | 2 | 4 | 4 | 8 | 5 | 5 | 5 | 4 | 6 | 6 |
| P21 | 5 | 7 | 6 | 7 | 5 | 8 | 8 | 7 | 5 | 7 |
| P22 | 8 | 9 | 6 | 7 | 7 | 8 | 6 | 8 | 8 | 8 |
| P23 | 5 | 6 | 6 | 7 | 5 | 3 | 7 | 3 | 4 | 3 |
| P24 | 5 | 5 | 6 | 7 | 7 | 4 | 6 | 3 | 7 | 6 |
| P25 | 5 | 5 | 7 | 8 | 7 | 6 | 7 | 5 | 4 | 7 |
| P26 | 3 | 5 | 4 | 7 | 3 | 1 | 2 | 6 | 6 | 5 |
| P27 | 4 | 3 | 6 | 8 | 6 | 1 | 8 | 2 | 7 | 7 |
| P28 | 3 | 8 | 4 | 8 | 6 | 2 | 8 | 4 | 6 | 1 |
| P29 | 3 | 5 | 1 | 5 | 5 | 3 | 4 | 6 | 7 | 5 |
| P30 | 3 | 8 | 5 | 8 | 7 | 5 | 5 | 3 | 7 | 8 |
| P31 | 8 | 8 | 5 | 7 | 9 | 9 | 7 | 7 | 6 | 8 |
| P32 | 7 | 6 | 2 | 2 | 6 | 6 | 2 | 7 | 5 | 5 |
Subiremos los datos al sistema.
Haremos el análisis de conglomerados. Configuramos conforme la figura abajo.

Al hacer clic en calcular obtenemos los resultados. También se puede descargar el archivo con los resultados en formato word.

Los resultados son:
Agrupación: método K medias
| Grupo 1 | Grupo 2 |
|---|---|
| P1 | P3 |
| P2 | P7 |
| P4 | P10 |
| P5 | P13 |
| P6 | P16 |
| P8 | P17 |
| P9 | P18 |
| P11 | P20 |
| P12 | P23 |
| P14 | P24 |
| P15 | P25 |
| P19 | P26 |
| P21 | P27 |
| P22 | P28 |
| P31 | P29 |
| P32 | P30 |
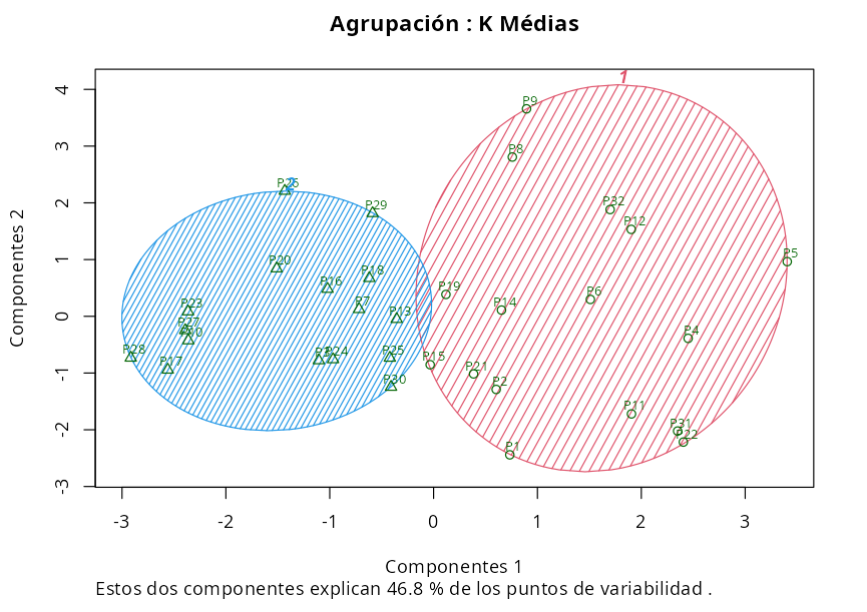
Ten en cuenta que el método K Medias agrupó a los clientes en 2 grupos. Podemos crear una tabla con las puntuaciones medias que cada grupo dio a las marcas de cerveza.
En el Grupo 1, las cervezas "oscuras" con un sabor "más fuerte" un promedio más alto;
En el Grupo 2, las cervezas de colores "claros" tuvieron la media más alta.
Una posible conclusión de esta segmentación es la siguiente: los clientes clasificados en el Grupo 1 tienen mayor preferencia por cervezas oscuras con un sabor más intenso, mientras que los clientes clasificados en el Grupo 2 tienen mayor preferencia por las cervezas de color "claro".