3. Componentes Principales
El Análisis de Componentes Principales es un método utilizado para reducir la dimensión del problema en componentes no correlacionados que son combinaciones lineales de las variables originales. El número de estos componentes es menor o igual que el número de variables originales. Este método es útil cuando el número de variables a estudiar es muy grande.
La herramienta Componentes principales de Action permite reducir la dimensión de los datos a través de componentes que son combinaciones lineales de las variables originales.
Ejemplo 1:
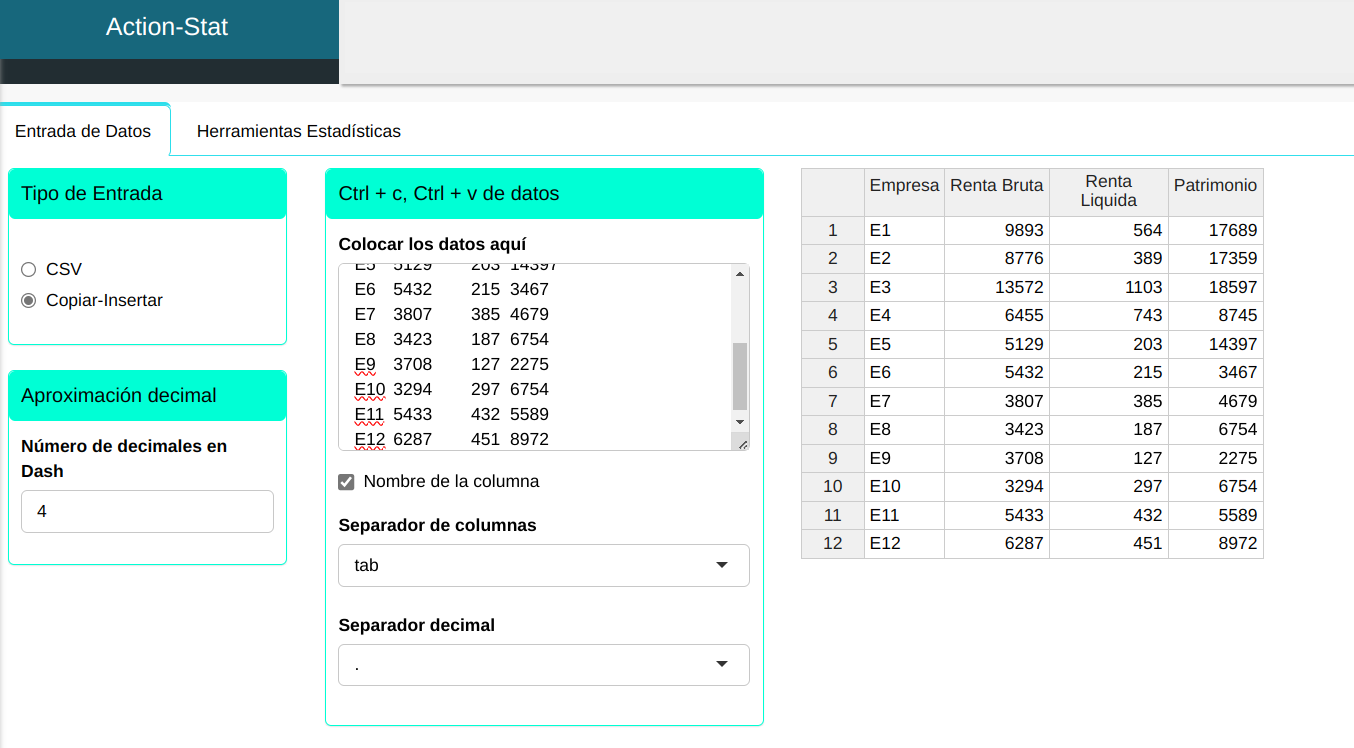
El cuadro representa la renta bruta, la renta líquida y el patrimonio, medidos en unidades monetarias de 12 empresas.
| Empresa | Renta Bruta | Renta Líquida | Patrimonio |
|---|---|---|---|
| E1 | 9893 | 564 | 17689 |
| E2 | 8776 | 389 | 17359 |
| E3 | 13572 | 1103 | 18597 |
| E4 | 6455 | 743 | 8745 |
| E5 | 5129 | 203 | 14397 |
| E6 | 5432 | 215 | 3467 |
| E7 | 3807 | 385 | 4679 |
| E8 | 3423 | 187 | 6754 |
| E9 | 3708 | 127 | 2275 |
| E10 | 3294 | 297 | 6754 |
| E11 | 5433 | 432 | 5589 |
| E12 | 6287 | 451 | 8972 |
Subiremos los datos al sistema.
Realizaremos el análisis de componentes principales, configurando conforme la figura abajo.

Clicando en calcular obtenemos los resultados. También se puede descargar los resultados en un archivo en formato Word.
Los resultados son:
Importancia de los componentes
| Información | Comp.1 | Comp.2 | Comp.3 |
|---|---|---|---|
| Desviación Estándar | 6165.8894 | 1525.7397 | 139.0497 |
| Proporción de la varianza | 0.9419 | 0.0577 | 0.00 |
| Proporción Acumulada | 0.9419 | 0.9995 | 1 |
Cuadro de centros de los componentes
| Valor del centro | |
|---|---|
| Renta Bruta | 6267.41667 |
| Renta Liquída | 424.6667 |
| Patrimonio | 9606.4167 |
Matriz de correlación
| Comp.1 | Comp.2 | Comp.3 | |
|---|---|---|---|
| Comp.1 | 1 | 0 | 0 |
| Comp.2 | 0 | 1 | 0 |
| Comp.3 | 0 | 0 | 1 |
Resultado del análisis
| Comp.1 | Comp.2 | Comp.3 | |
|---|---|---|---|
| Renta bruta | 0.425 | 0.900 | 0.099 |
| Renta.Líquida | 0.028 | 0.097 | -0.995 |
| Patrimonio | 0.905 | -0.426 | -0.016 |
Resultado del análisis
| Comp.1 | Comp.2 | Comp.3 | |
|---|---|---|---|
| E1 | 8857.594 | -165.267 | 90.180 |
| E2 | 8079.361 | -1046.652 | 158.932 |
| E3 | 11257.926 | 2810.250 | -96.180 |
| E4 | -690.799 | 566.191 | -284.231 |
| E5 | 3844.091 | -3084.941 | 30.403 |
| E6 | -5915.416 | 1841.624 | 224.925 |
| E7 | -5504.970 | -119.929 | -124.811 |
| E8 | -3796.380 | -1367.834 | 0.640 |
| E9 | -7729.150 | 789.459 | 160.881 |
| E10 | -3848.175 | -1473.279 | -121.587 |
| E11 | -3989.162 | 960.153 | -25.133 |
| E12 | -564.919 | 290.226 | -14.019 |
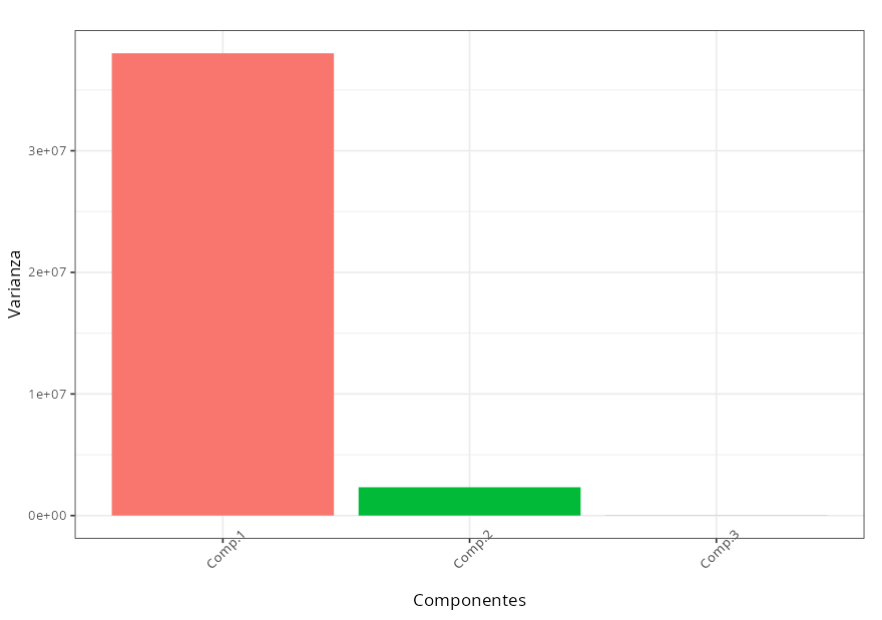
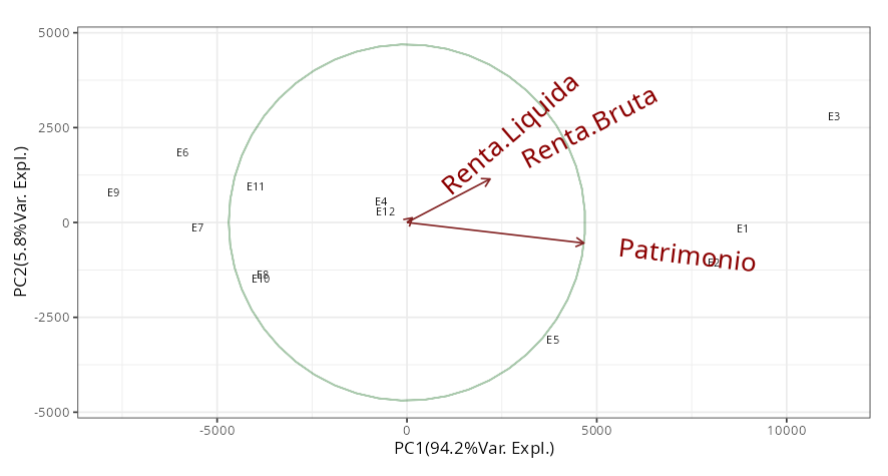
El primer componente principal explica el 94.18% de la variación total. Las variables renta bruta y patrimonio tienen ponderaciones negativamente altas en el primer componente principal, -0.425 y -0.905 respectivamente; la variable renta líquida prácticamente no afecta este componente, ya que su peso es muy bajo, -0.02.
Así, el primer componente puede interpretarse como un índice de desempeño global de las empresas. Como las ponderaciones son negativas, cuanto mayores sean las rentas brutas y el patrimonio de la empresa, menor será el valor de este componente y mejor será el índice de desempeño general de la empresa. Las empresas E3, E1 y E2 tuvieron los mejores índices de desempeño, respectivamente, mientras que la empresa con el peor índice fue E9.
Ejemplo 2:
Cinco jueces evaluaron 8 marcas de una comida brasileña llamada “coxinha de pollo” en relación con sabor, aroma, calidad de la masa y calidad del relleno. Cada juez dio una puntuación del 1 al 5 que representa la calidad de los muslos. El cuadro contiene las puntuaciones de los jueces sobre la calidad de cada marca de muslo (Coxinha).
| Marca | Sabor | Aroma | Masa | Relleno |
|---|---|---|---|---|
| M1 | 2.75 | 4.03 | 2.8 | 2.62 |
| M2 | 3.9 | 4.12 | 3.4 | 3.52 |
| M3 | 3.12 | 3.97 | 3.62 | 3.05 |
| M4 | 4.58 | 4.86 | 4.34 | 4.82 |
| M5 | 3.97 | 4.34 | 4.28 | 4.98 |
| M6 | 3.01 | 3.98 | 2.9 | 2.82 |
| M7 | 4.19 | 4.65 | 4.52 | 4.77 |
| M8 | 3.82 | 4.12 | 3.62 | 3.71 |
Subiremos los datos al sistema.
Realizaremos el análisis de componentes principales, configurando conforme a figura abajo.

Clicando en calcular obtenemos los resultados. También se puede descargar los resultados en un archivo Word.
Los resultados son:
Importancia de los componentes
| Información | Comp.1 | Comp.2 | Comp.3 | Comp.4 |
|---|---|---|---|---|
| Desviación Estándar | 1.905 | 0.442 | 0.361 | 0.210 |
| Proporción de varianza | 0.908 | 0.049 | 0.033 | 0.011 |
| Proporción Acumulada | 0.908 | 0.956 | 0.989 | 1 |
Cuadro de los centros de los componentes
| Valor del centro | |
|---|---|
| Sabor | 3.668 |
| Aroma | 4.259 |
| Masa | 3.685 |
| Relleno | 3.786 |
Matriz de Correlación
| Comp.1 | Comp.2 | Comp.3 | Comp.4 | |
|---|---|---|---|---|
| Comp.1 | 1 | 0 | 0 | 0 |
| Comp.2 | 0 | 1 | 0 | 0 |
| Comp.3 | 0 | 0 | 1 | 0 |
| Comp.4 | 0 | 0 | 0 | 1 |
Resultado del análisis
| Comp.1 | Comp.2 | Comp.3 | Comp.4 | |
|---|---|---|---|---|
| Sabor | 0.499 | 0.153 | 0.825 | 0.216 |
| Aromas | 0.488 | 0.756 | -0.436 | 0.003 |
| Masa | 0.502 | -0.532 | -0.357 | 0.582 |
| Relleno | 0.511 | -0.349 | -0.039 | -0.784 |
Resultado del análisis
| Comp.1 | Comp.2 | Comp.3 | Comp.4 | |
|---|---|---|---|---|
| M1 | -2.523 | 0.437 | -0.378 | -0.154 |
| M2 | -0.410 | 0.075 | 0.695 | 0.045 |
| M3 | -1.386 | -0.498 | -0.281 | 0.384 |
| M4 | 2.838 | 0.721 | -0.011 | 0.053 |
| M5 | 1.554 | -0.711 | -0.097 | -0.371 |
| M6 | -2.187 | 0.216 | -0.016 | -0.141 |
| M7 | 2.302 | -0.028 | -0.359 | 0.126 |
| M8 | -0.187 | -0.212 | 0.447 | 0.059 |
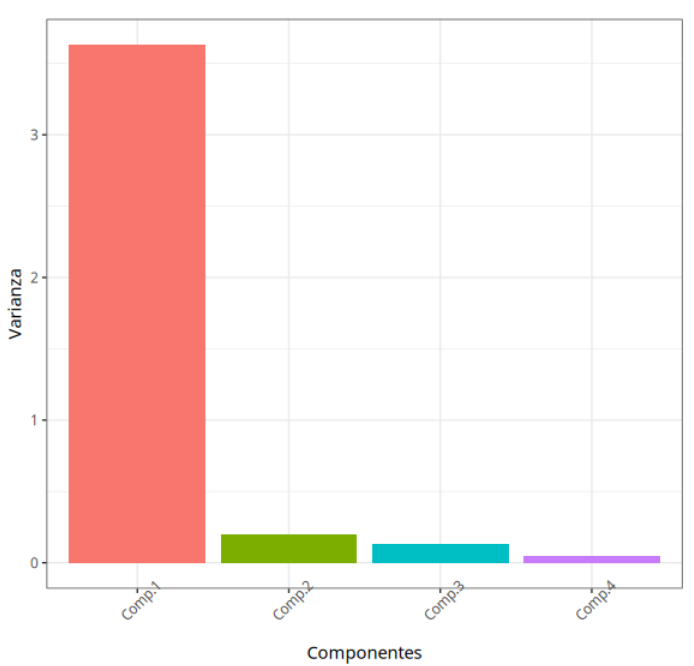
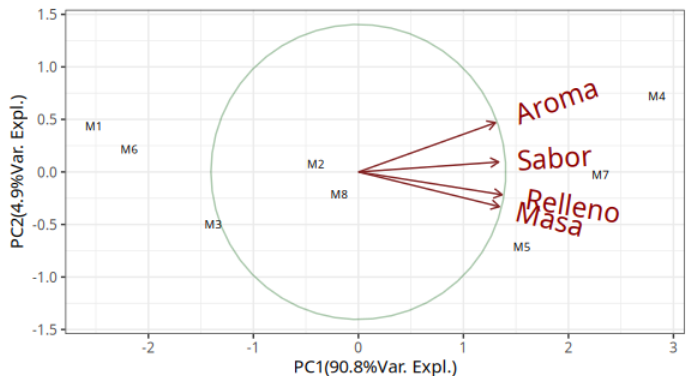
El primer componente principal explica el 90.8% de la variación total y según el cuadro de vectores propios, los pesos de las variables masa, relleno, sabor y el aroma son negativamente altos para este componente. En otras palabras, cuanto mayor sea la puntuación de estas variables, menor será la puntuación del primer componente. Así, el primer componente principal puede entenderse como índice global de la calidad de los muslos (coxinha) según los jueces.
De esta forma, una puntuación más baja en el primer componente indica que el índice de la calidad es mejor, es decir, cuanto menor sea la puntuación de este componente, mejor es la coxinha. Según el cuadro de puntuación obtenida en este análisis, las marcas M4, M5 y M7 tienen las mejores coxinhas mientras que la marca M1 tiene la peor coxinha.
Ejemplo 3:
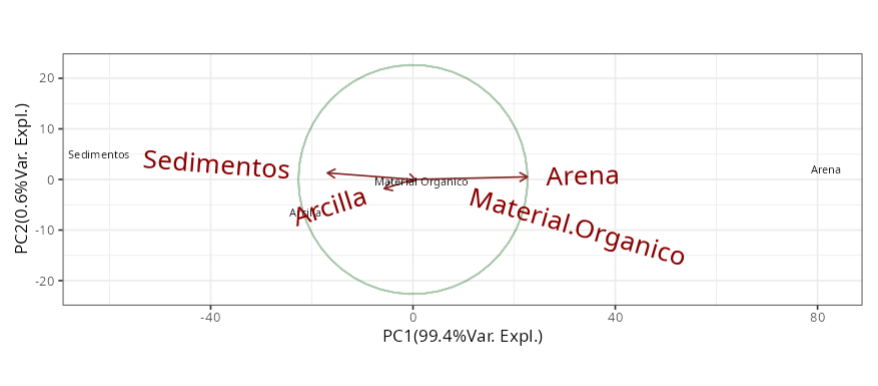
Un estudio se recopiló 25 muestras de un determinado suelo. Para cada muestra se midió el porcentaje de arena (X1), sedimentos (X2), arcilla (X3) y la cantidad de materia orgánica (X4). La matriz de covarianza de datos analizada se encuentra en la tabla.
| Arena | Sedimentos | Arcilla | Materia Orgánica | |
|---|---|---|---|---|
| Arena | 64.96 | -47.22 | -17.74 | 1.58 |
| Sedimentos | -47.22 | 38.8 | 8.42 | -1.62 |
| Arcilla | -17.74 | 8.42 | 9.31 | 0.04 |
| Materia Orgánica | 1.58 | -1.62 | 0.04 | 0.68 |
Subiremos los datos al sistema.
Realizaremos análisis de componentes principales, configurando conforme la figura abajo.
Clicando en calcular obtenemos los resultados. También se puede descargar los resultados en un archivo Word.
Los resultados son:
Importancia de los componentes
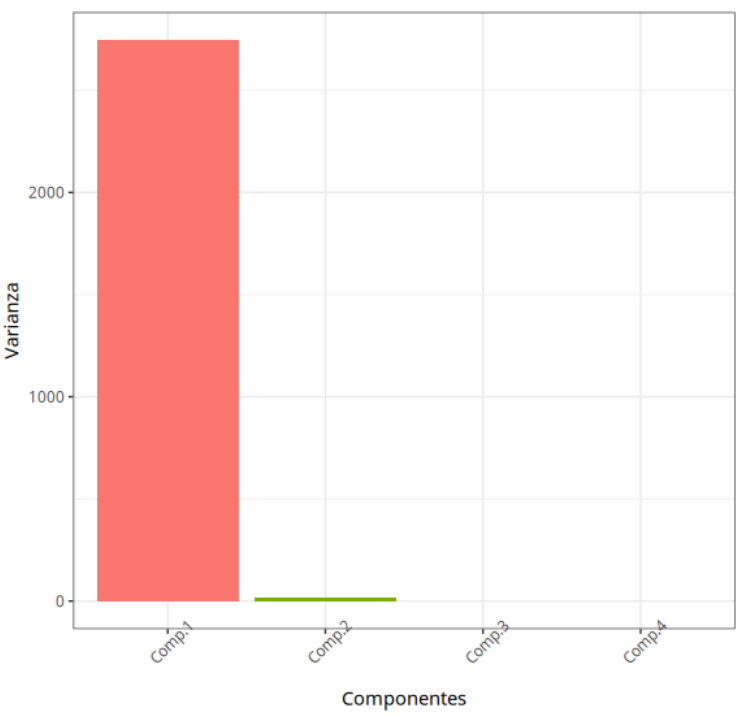
| Información | Comp.1 | Comp.2 | Comp.3 | Comp.4 |
|---|---|---|---|---|
| Desviación Estándar | 52.397 | 4.180 | 0.255 | 0 |
| Proporción de varianza | 0.994 | 0.006 | 0.000 | 0 |
| Proporción acumulada | 0.994 | 1.000 | 1.000 | 1 |
Cuadro de centros de componentes
| Valor central | |
|---|---|
| Arena | 0.395 |
| Sedimentos | -0.405 |
| Arcilla | 0.008 |
| Materia Orgánica | 0.170 |
Matriz de correlación
| Comp.1 | Comp.2 | Comp.3 | Comp.4 | |
|---|---|---|---|---|
| Comp.1 | 1.00 | 0.000 | 0.000 | 0.050 |
| Comp.2 | 0.00 | 1.000 | 0.000 | -0.548 |
| Comp.3 | 0.00 | 0.000 | 1.000 | -0.835 |
| Comp.4 | 0.05 | -0.548 | -0.835 | 1.000 |
Resultado del análisis
| Comp.1 | Comp.2 | Comp.3 | Comp.4 | |
|---|---|---|---|---|
| Arena | 0.785 | 0.226 | 0.003 | 0.577 |
| Sedimentos | -0.587 | 0.565 | 0.057 | 0.577 |
| Arcilla | -0.198 | -0.790 | -0.053 | 0.578 |
| Materia Orgánica | 0.021 | -0.075 | 0.997 | -0.004 |
Resultado del análisis
| Comp.1 | Comp.2 | Comp.3 | Comp.4 | |
|---|---|---|---|---|
| Arena | 81.689 | 2.045 | -0.146 | 0 |
| Sedimentos | -62.083 | 4.886 | -0.122 | 0 |
| Arcilla | -21.253 | -6.449 | -0.172 | 0 |
| Materia orgánica | 1.648 | -0.483 | 0.440 | 0 |