6. MANOVA
El análisis multivariado de varianza (MANOVA) es una forma generalizada del análisis de varianza (ANOVA). Se utiliza en los casos en que existen dos o más variables dependientes.
Ejemplo 1:
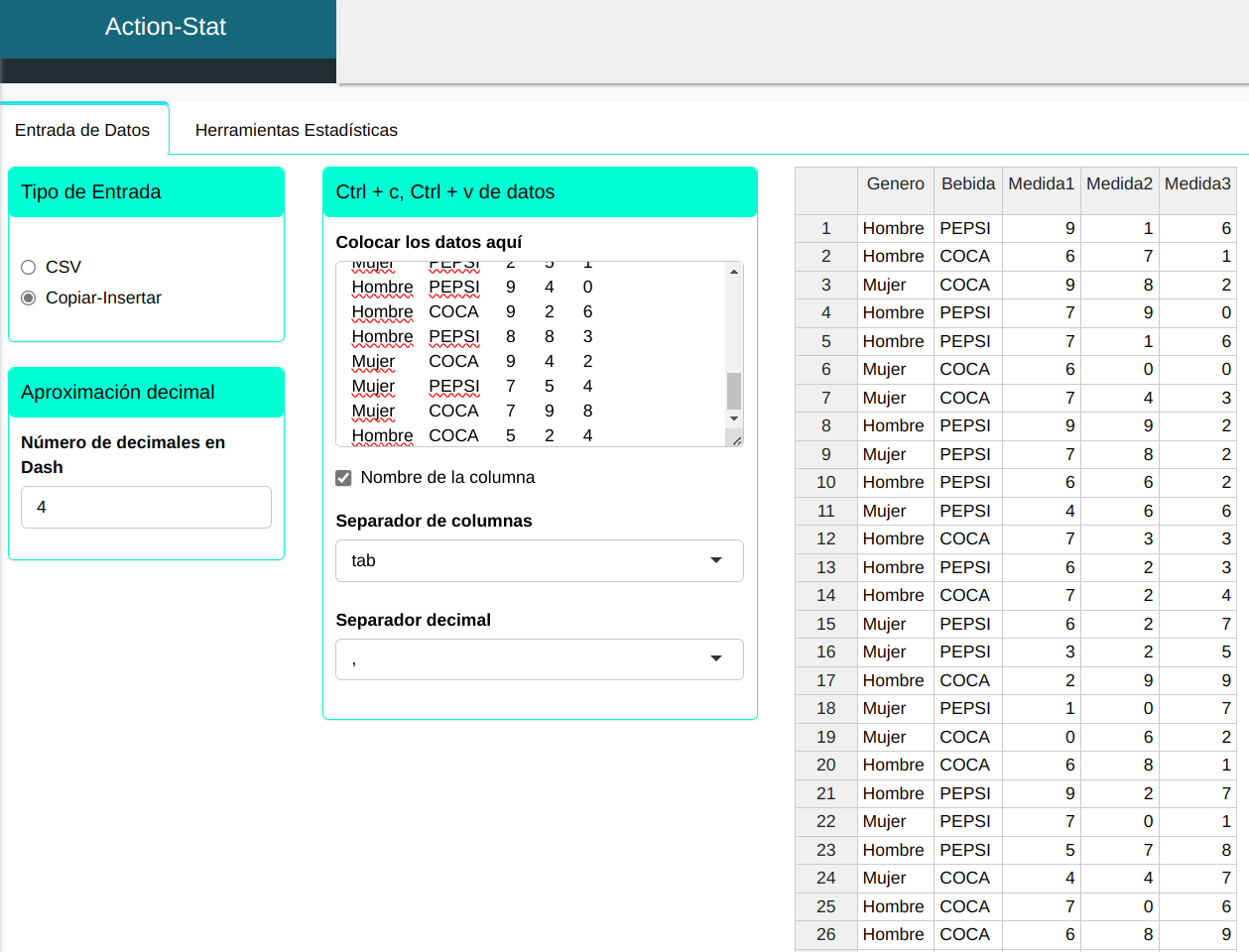
Cada fila del siguiente cuadro representa un gerente de compras de grandes cadenas de restaurantes. La columna género identifica el género del gerente, la columna bebida identifica la bebida servida "Coca" o "Pepsi" y las variables Medida1, Medida2 y Medida3 contienen información relacionada a las compras de la compañía durante los últimos 23 meses.
El objetivo del análisis es identificar si algún gerente compró más que otro y si una bebida se compró más que la otra. Utilizaremos MANOVA para analizar el modelo de 1º orden com interacción 2-way de las variables Género y Bebida.
| Género | Bebida | Medida1 | Medida2 | Medida3 |
|---|---|---|---|---|
| Hombre | PEPSI | 9 | 1 | 6 |
| Hombre | COCA | 6 | 7 | 1 |
| Mujer | COCA | 9 | 8 | 2 |
| Hombre | PEPSI | 7 | 9 | 0 |
| Hombre | PEPSI | 7 | 1 | 6 |
| Mujer | COCA | 6 | 0 | 0 |
| Mujer | COCA | 7 | 4 | 3 |
| Hombre | PEPSI | 9 | 9 | 2 |
| Mujer | PEPSI | 7 | 8 | 2 |
| Hombre | PEPSI | 6 | 6 | 2 |
| Mujer | PEPSI | 4 | 6 | 6 |
| Hombre | COCA | 7 | 3 | 3 |
| Hombre | PEPSI | 6 | 2 | 3 |
| Hombre | COCA | 7 | 2 | 4 |
| Mujer | PEPSI | 6 | 2 | 7 |
| Mujer | PEPSI | 3 | 2 | 5 |
| Hombre | COCA | 2 | 9 | 9 |
| Mujer | PEPSI | 1 | 0 | 7 |
| Mujer | COCA | 0 | 6 | 2 |
| Hombre | COCA | 6 | 8 | 1 |
| Hombre | PEPSI | 9 | 2 | 7 |
| Mujer | PEPSI | 7 | 0 | 1 |
| Hombre | PEPSI | 5 | 7 | 8 |
| Mujer | COCA | 4 | 4 | 7 |
| Hombre | COCA | 7 | 0 | 6 |
| Hombre | COCA | 6 | 8 | 9 |
| Hombre | PEPSI | 5 | 1 | 6 |
| Mujer | PEPSI | 5 | 1 | 6 |
| Mujer | PEPSI | 7 | 5 | 2 |
| Hombre | COCA | 3 | 6 | 0 |
| Hombre | PEPSI | 2 | 3 | 9 |
| Mujer | COCA | 1 | 7 | 2 |
| Mujer | PEPSI | 9 | 7 | 8 |
| Hombre | COCA | 9 | 2 | 2 |
| Hombre | COCA | 7 | 9 | 8 |
| Hombre | COCA | 5 | 3 | 5 |
| Mujer | PEPSI | 7 | 6 | 5 |
| Mujer | PEPSI | 6 | 7 | 3 |
| Mujer | PEPSI | 5 | 1 | 3 |
| Hombre | COCA | 7 | 6 | 2 |
| Hombre | PEPSI | 3 | 5 | 2 |
| Hombre | COCA | 5 | 5 | 7 |
| Mujer | PEPSI | 2 | 5 | 1 |
| Hombre | PEPSI | 9 | 4 | 0 |
| Hombre | COCA | 9 | 2 | 6 |
| Hombre | PEPSI | 8 | 8 | 3 |
| Mujer | COCA | 9 | 4 | 2 |
| Mujer | PEPSI | 7 | 5 | 4 |
| Mujer | COCA | 7 | 9 | 8 |
| Hombre | COCA | 5 | 2 | 4 |
Subiremos los datos al sistema.
Realizaremos el análisis de MANOVA. Configuramos conforme la figura abajo.
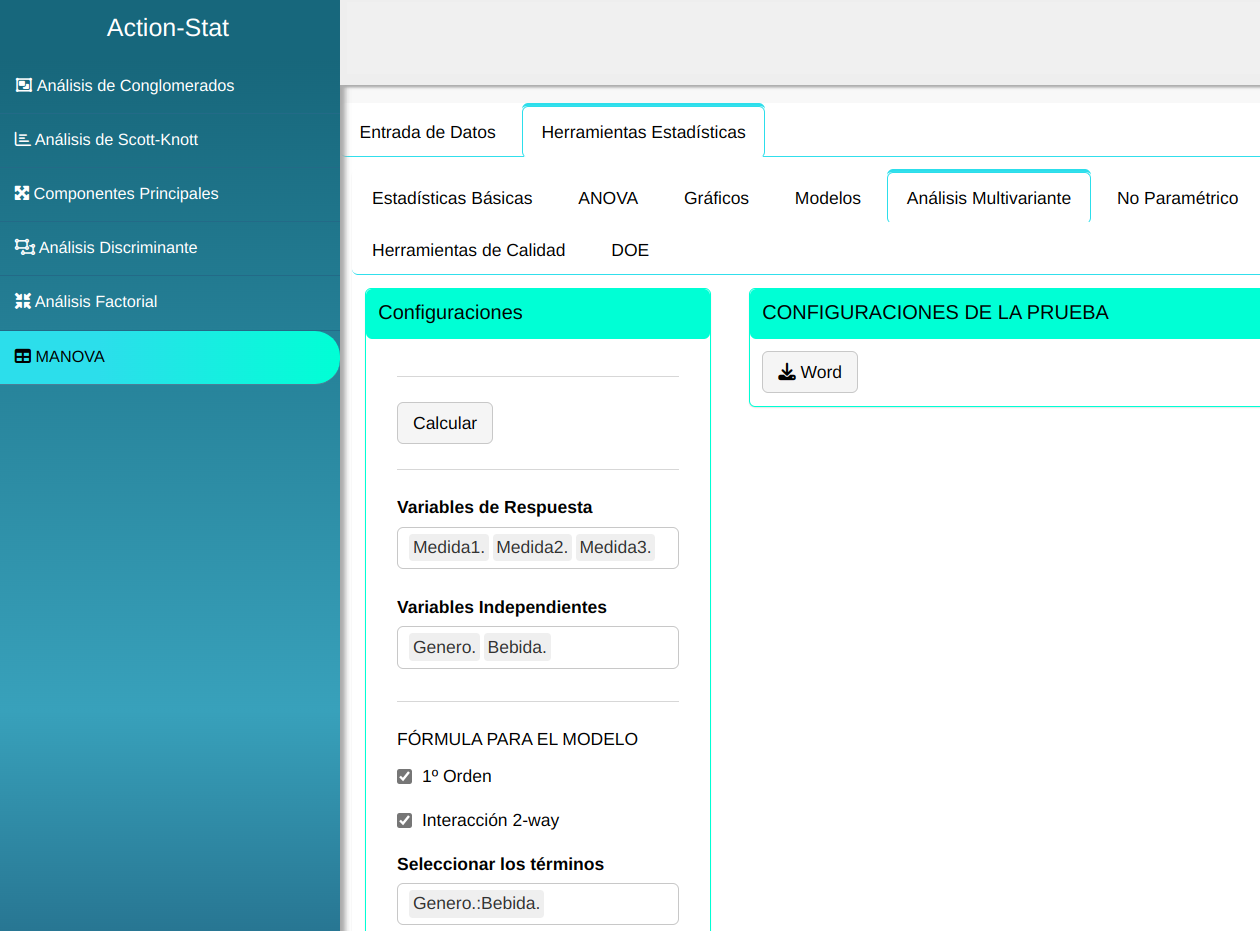

Clicando en calcular obtenemos los resultados. También se puede descargar los resultados en un archivo en formato Word.
Los resultados son:
Cuadro de promedios por grupo
| Grupos | Beber | Medida1 | Medida2 | Medida3 |
|---|---|---|---|---|
| Hombre | COCA | 6.067 | 4.800 | 4.467 |
| Mujer | COCA | 5.375 | 5.250 | 3.250 |
| Hombre | PEPSI | 6.538 | 4.462 | 4.154 |
| Mujer | PEPSI | 5.429 | 3.929 | 4.286 |
Matriz de covarianza
| Medida1 | Medida2 | Medida3 | |
|---|---|---|---|
| Medida1 | 5.602 | 0.096 | -0.680 |
| Medida2 | 0.096 | 8.335 | -0.465 |
| Medida3 | -0.680 | -0.465 | 7.429 |
Cuadro MANOVA
| GL | Estad.Wilks | Estad.F | GL.Numerador | G.L.Denominador | P-valor | |
|---|---|---|---|---|---|---|
| Género | 1 | 0.954 | 0.703 | 3 | 44 | 0.555 |
| Bebida | 1 | 0.977 | 0.349 | 3 | 44 | 0.790 |
| Género:Bebida | 1 | 0.978 | 0.324 | 3 | 44 | 0.808 |
| Residuos | 46 |
Utilizando las pruebas de Wilks en el cuadro MANOVA. podemos concluir que no existe diferencia significativa en las compras en los últimos 23 meses por el factor bebida y el factor género. La interacción tampoco es significativa.
Ejemplo 2:
Se realizaron dos grupos/tipos de tratamiento (A y B) en una muestra con cuatro mediciones a intervalos de tiempo equidistantes. El tratamiento A corresponde al tratamiento activo y el B, al placebo.
Preguntas de interés:
-
En general, ¿existen diferencias significativas entre los puntos de TIEMPO?
-
¿Los dos grupos difieren en algún punto, es decir, hay algún efecto del tratamiento?
-
¿Los dos grupos difieren en sus respuestas a lo largo del tiempo, es decir, hay una interacción TIEMPO * TRATAMIENTO?
Premisa:
-
Tanto ANOVA como MANOVA de medidas repetidas suponen que los intervalos de tiempo están igualmente espaciados.
-
Ambos métodos asumen que la respuesta se distribuye normalmente, pero ambos enfoques son robustos frente a violaciones de la normalidad.
-
Ambos enfoques requieren datos completos sobre todos los asuntos es decir, que no falten observaciones para cualquier asunto.
| Grupo | Tiempo1 | Tiempo2 | Tiempo3 | Tiempo4 |
|---|---|---|---|---|
| A | 31 | 29 | 15 | 26 |
| A | 24 | 28 | 20 | 32 |
| A | 14 | 20 | 28 | 30 |
| B | 38 | 34 | 30 | 34 |
| B | 25 | 29 | 25 | 29 |
| B | 30 | 28 | 16 | 34 |
Subiremos los datos al sistema.
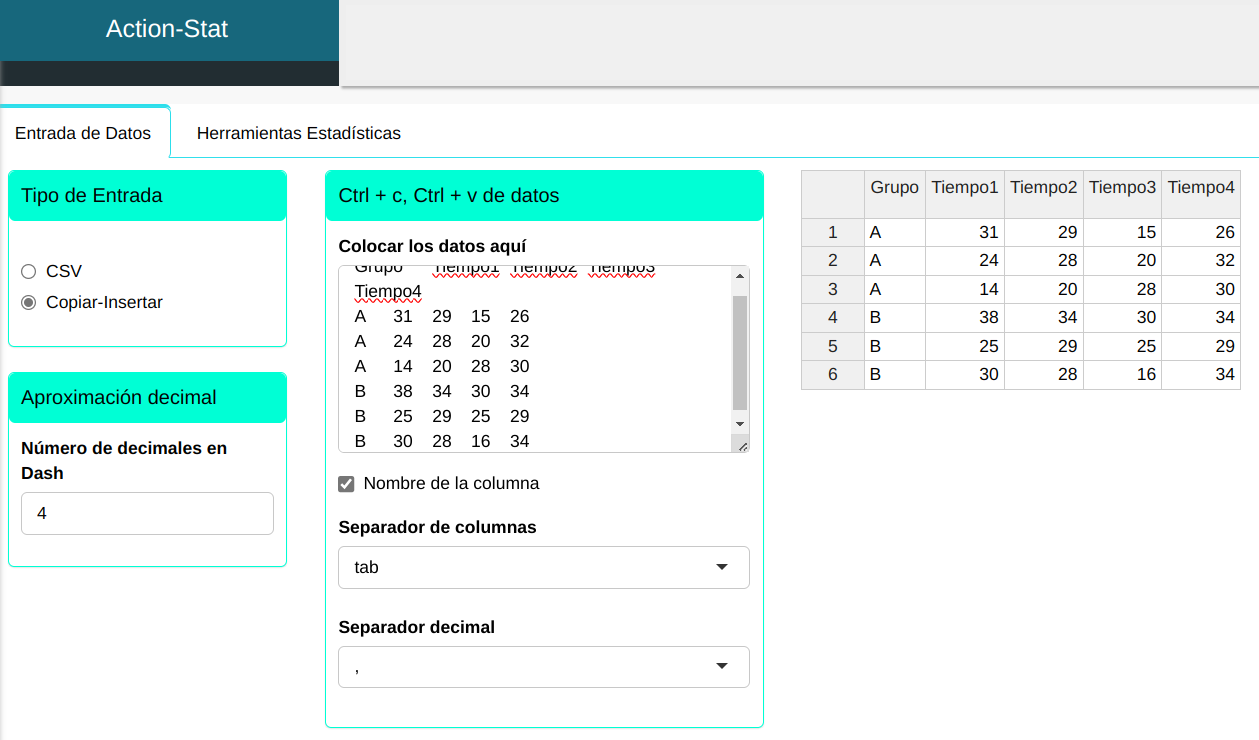
Realizaremos el análisis de MANOVA. Configuramos conforme la figura abajo.

Clicando en calcular obtenemos los resultados. También se puede descargar los resultados en un archivo en formato Word.
Los resultados son:
Cuadro de las Medias por grupo
| Grupos | Tiempo1 | Tiempo2 | Tiempo3 | Tiempo4 |
|---|---|---|---|---|
| A | 23 | 25.667 | 21 | 29.333 |
| B | 31 | 30.333 | 23.667 | 32.333 |
Matriz de Covarianza
| Tiempo1 | Tiempo2 | Tiempo3 | Tiempo4 | |
|---|---|---|---|---|
| Tiempo1 | 65.6 | 34.4 | -7.200 | 7.200 |
| Tiempo2 | 34.4 | 20.4 | -0.800 | 3.800 |
| Tiempo3 | -7.2 | -0.8 | 39.467 | 5.467 |
| Tiempo4 | 7.2 | 3.8 | 5.467 | 9.767 |
Cuadro de MANOVA
| G.L. | Estd.Wilks | Estad.F | GL.Numerador | GL.Denominador | P-valor | |
|---|---|---|---|---|---|---|
| Grupo | 1 | 0.508 | 0.242 | 4 | 1 | 0.888 |
| Residuos | 4 |
Cuadro ANOVA: Tiempo1
| G.L. | Suma de Cuadrados | Cuadrado Medio | Estad. F | P-valor | |
|---|---|---|---|---|---|
| Grupo | 1 | 96 | 96 | 1.655 | 0.268 |
| Residuos | 4 | 232 | 58 |
Cuadro ANOVA: Tiempo2
| G.L. | Suma de Cuadrados | Cuadrado Medio | Estad.F | P-valor | |
|---|---|---|---|---|---|
| Grupo | 1 | 32.667 | 32.667 | 1.885 | 0.242 |
| Residuos | 4 | 69.333 | 17.333 |
Cuadro ANOVA: Tiempo3
| G.L. | Suma de Cuadrados | Cuadrado Medio | Estad.F | P-palor | |
|---|---|---|---|---|---|
| Grupo | 1 | 10.667 | 10.667 | 0.229 | 0.658 |
| Residuos | 4 | 186.667 | 46.667 |
Cuadro ANOVA: Tiempo4
| G.L. | Suma de Cuadrados | Cuadrado Medio | Estad. F | P-valor | |
|---|---|---|---|---|---|
| Grupo | 1 | 13.500 | 13.500 | 1.528 | 0.284 |
| Residuos | 4 | 35.333 | 8.833 |