2. ANOVA Efecto Mixto
ANOVA se utiliza para analizar el comportamiento de varios tratamientos de un factor aplicado al proceso y/o producto.
Ejemplo 1:
Considere el proceso de medir el diámetro del rodamiento de un motor. Los datos están a continuación:
| Piezas | Medidas |
|---|---|
| 1 | 461.28 |
| 2 | 458.17 |
| 3 | 460.57 |
| 4 | 459.28 |
| 5 | 461.28 |
| 6 | 460.25 |
| 7 | 458.82 |
| 8 | 461.58 |
| 9 | 459.36 |
| 10 | 459.62 |
| 11 | 461.38 |
| 12 | 458.67 |
| 13 | 462.57 |
| 14 | 459.58 |
| 15 | 461.76 |
| 1 | 461.50 |
| 2 | 458.62 |
| 3 | 460.28 |
| 4 | 459.66 |
| 5 | 461.12 |
| 6 | 460.68 |
| 7 | 458.95 |
| 8 | 461.10 |
| 9 | 459.52 |
| 10 | 459.34 |
| 11 | 461.57 |
| 12 | 459.03 |
| 13 | 462.28 |
| 14 | 459.66 |
| 15 | 461.12 |
| 1 | 461.20 |
| 2 | 458.61 |
| 3 | 460.32 |
| 4 | 459.58 |
| 5 | 461.18 |
| 6 | 460.28 |
| 7 | 458.66 |
| 8 | 461.18 |
| 9 | 459.57 |
| 10 | 459.54 |
| 11 | 461.53 |
| 12 | 458.98 |
| 13 | 462.32 |
| 14 | 459.28 |
| 15 | 461.15 |
Subiremos los datos al sistema.
Para realizar el ANOVA de efectos mixtos, se realiza la siguiente configuración, tal y como se muestra en la siguiente figura.
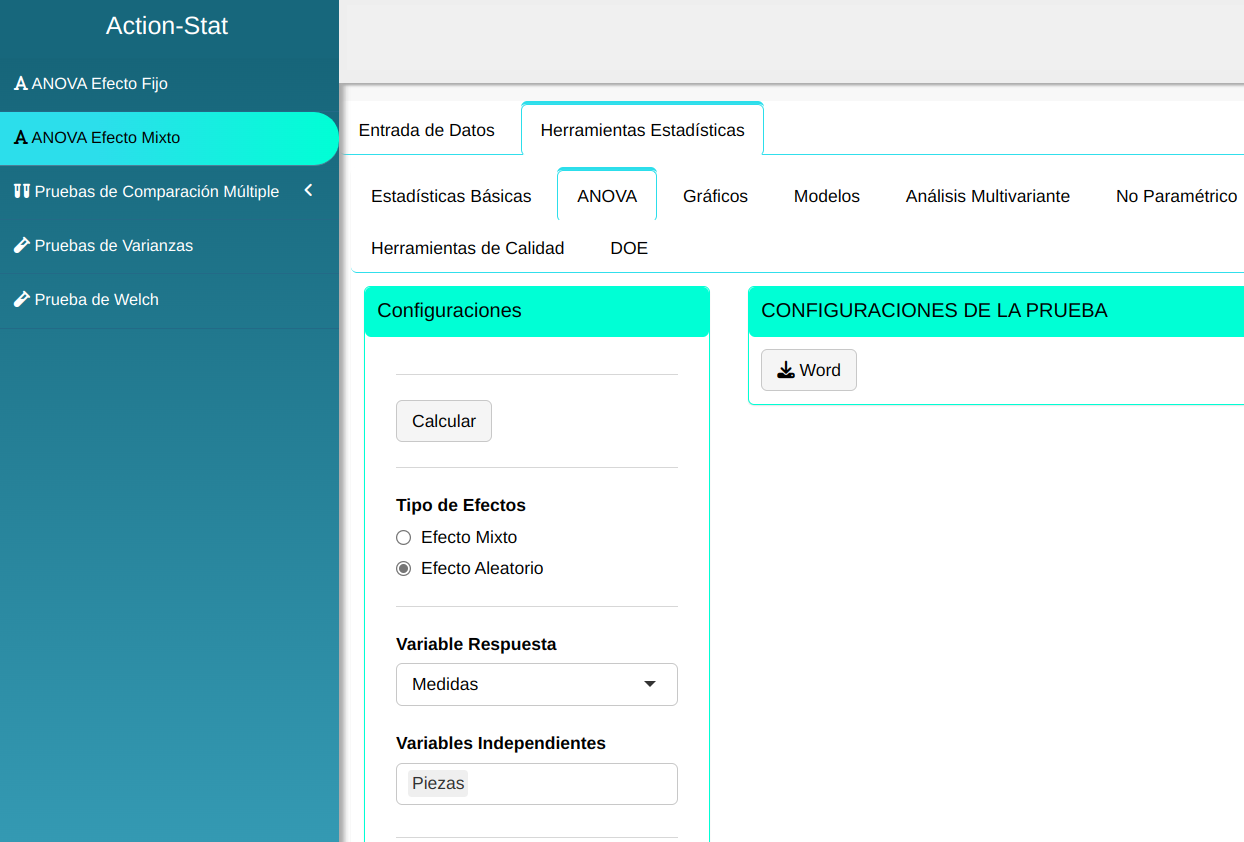
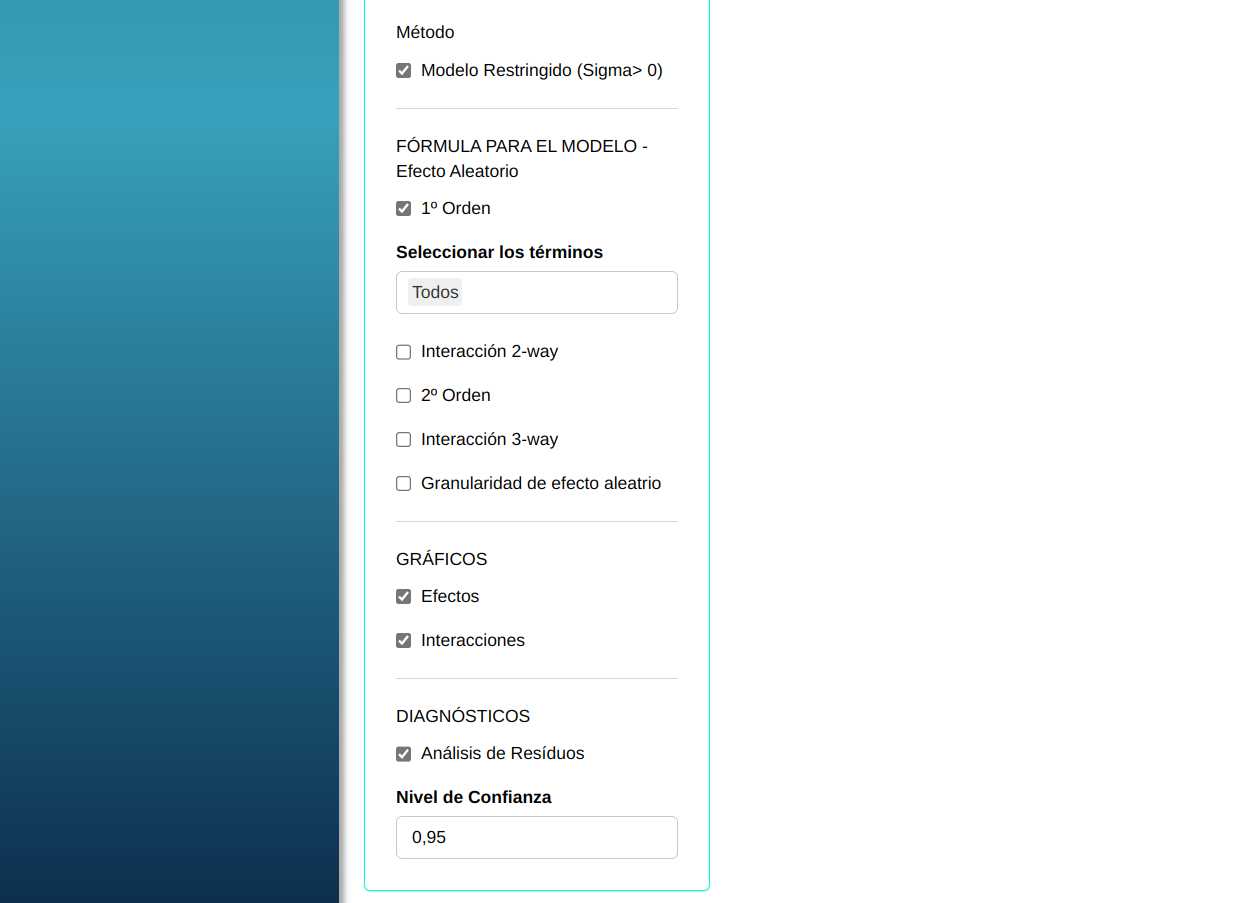
En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:
ANOVA con efecto aleatorio - Modelo Restringido (Sigma > 0)
| Factores | Desviación Estándar | X-squared | GL | P-valor | |
|---|---|---|---|---|---|
| X | Piezas | 1.18479 | 91.326 | 1 | 0 |
| X.1 | Resíduos | 0.19707 |
Intervalo de confianza del Efecto Piezas
| Nivel | Límite Inferior | Efecto para media | Límite Superior |
|---|---|---|---|
| 1 | 461.094 | 461.327 | 461.559 |
| 2 | 458.234 | 458.467 | 458.699 |
| 3 | 460.158 | 460.390 | 460.622 |
| 4 | 459.274 | 459.507 | 459.739 |
| 5 | 460.961 | 461.193 | 461.426 |
| 6 | 460.171 | 460.403 | 460.636 |
| 7 | 458.578 | 458.810 | 459.042 |
| 8 | 461.054 | 461.287 | 461.519 |
| 9 | 459.251 | 459.483 | 459.716 |
| 10 | 459.268 | 459.500 | 459.732 |
| 11 | 461.261 | 461.493 | 461.726 |
| 12 | 458.661 | 458.893 | 459.126 |
| 13 | 462.158 | 462.390 | 462.622 |
| 14 | 459.274 | 459.507 | 459.739 |
| 15 | 461.111 | 461.343 | 461.576 |
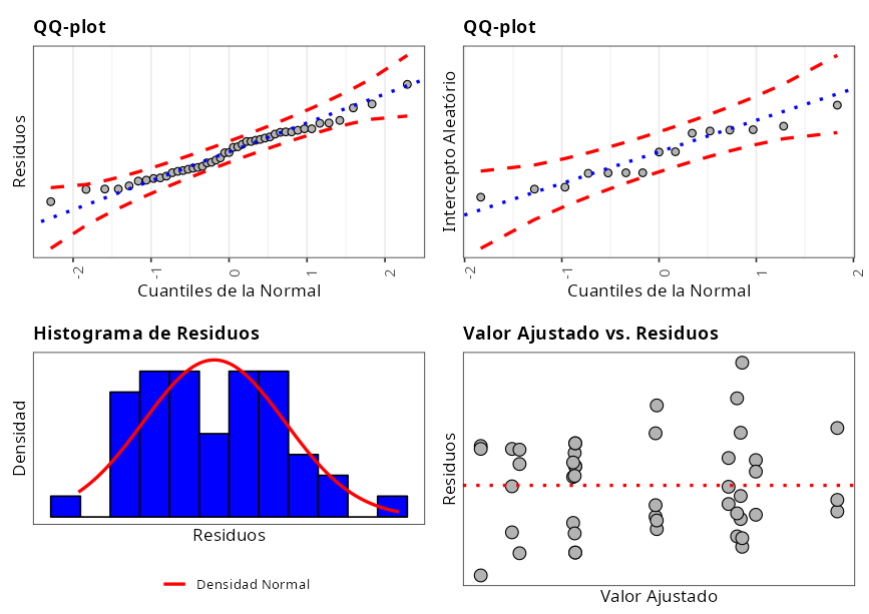
Prueba de la Normalidad - Residuos
| Valor | |
|---|---|
| Media | 0.000 |
| Desviación Estándar | 0.163 |
| N | 45.000 |
| Anderson-Darling | 0.370 |
| P-Valor | 0.412 |
Pruebas de Normalidad - Intercepto Aleatório
| Valor | |
|---|---|
| Media | 0.000 |
| Desviación Estándar | 1.179 |
| N | 15.000 |
| Anderson-Darling | 0.516 |
| P-Valor | 0.159 |
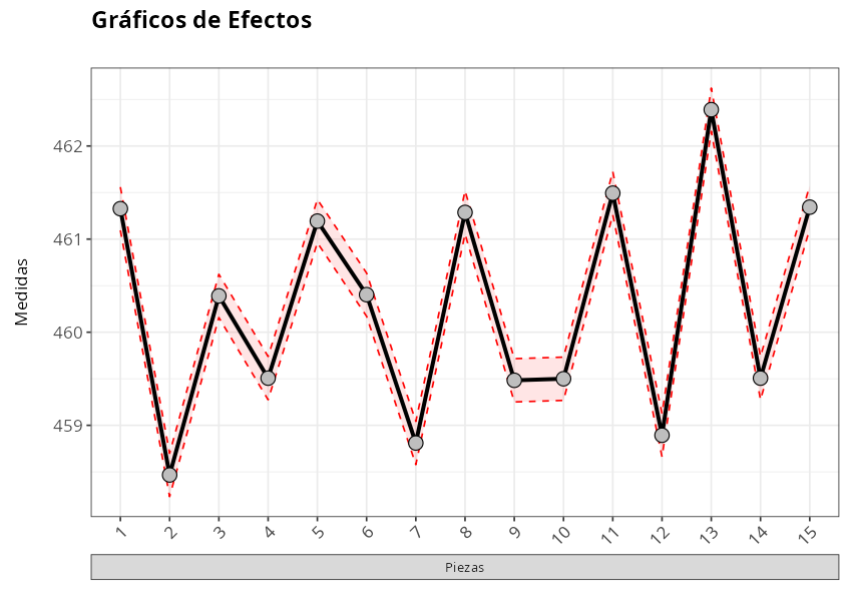
La tabla publicada indica que las piezas difieren, ya que el valor P referido a este factor (Piezas) es inferior al nivel de significancia predeterminado ($\alpha $), del 5%.
En el gráfico, los puntos negros son los promedios de cada nivel del factor, que en la tabla se denominan Efectos. Las líneas rojas representan el intervalo de confianza para las medias del nivel de factor.
No gráfico 4 plotamos um gráfico de Resíduos versus valores ajustados.
En el gráfico 1 se muestra un gráfico de Residuos versus Cuantiles Normales.
En el gráfico 2 se muestra un gráfico de intercepción aleatoria versus cuantiles normales.
En el gráfico 3 trazamos un histograma de los residuos para tener una idea de cómo se distribuyen los residuos.
En nuestro caso usaremos la prueba de Anderson-Darling, donde la hipótesis nula es la normalidad de los datos, y por ejemplo, verificamos que no rechazamos ("aceitamos") la hipótesis nula y con esto verificamos la normalidad de los residuales y la Intercepción Aleatoria.
Ejemplo 2:
Una empresa quiere probar la diferencia entre dos tipos de comida para perros (ración). 24 animales siguieron la dieta y fueron evaluados durante 6 días. En los primeros 3 días se ofreció un tipo de alimento (ración) y en los últimos 3 días otro tipo.
| Animal | Ración | Secuencia | Período | Consumido |
|---|---|---|---|---|
| 1 | 1 | AB | 1 | 99.65 |
| 2 | 1 | AB | 1 | 43.97 |
| 3 | 1 | AB | 1 | 68.65 |
| 4 | 1 | AB | 1 | 77.50 |
| 5 | 1 | AB | 1 | 100.00 |
| 6 | 1 | AB | 1 | 100.00 |
| 7 | 1 | AB | 1 | 97.47 |
| 8 | 1 | AB | 1 | 29.58 |
| 9 | 1 | AB | 1 | 100.00 |
| 10 | 1 | AB | 1 | 100.00 |
| 11 | 1 | AB | 1 | 100.00 |
| 12 | 1 | AB | 1 | 31.62 |
| 13 | 2 | BA | 1 | 100.00 |
| 14 | 2 | BA | 1 | 45.73 |
| 15 | 2 | BA | 1 | 61.56 |
| 16 | 2 | BA | 1 | 99.40 |
| 17 | 2 | BA | 1 | 36.77 |
| 18 | 2 | BA | 1 | 100.00 |
| 19 | 2 | BA | 1 | 100.00 |
| 20 | 2 | BA | 1 | 100.00 |
| 21 | 2 | BA | 1 | 89.78 |
| 22 | 2 | BA | 1 | 74.10 |
| 23 | 2 | BA | 1 | 37.09 |
| 24 | 2 | BA | 1 | 36.08 |
| 1 | 2 | AB | 2 | 100.00 |
| 2 | 2 | AB | 2 | 0.00 |
| 3 | 2 | AB | 2 | 44.97 |
| 4 | 2 | AB | 2 | 43.15 |
| 5 | 2 | AB | 2 | 100.00 |
| 6 | 2 | AB | 2 | 100.00 |
| 7 | 2 | AB | 2 | 100.00 |
| 8 | 2 | AB | 2 | 16.49 |
| 9 | 2 | AB | 2 | 100.00 |
| 10 | 2 | AB | 2 | 100.00 |
| 11 | 2 | AB | 2 | 100.00 |
| 12 | 2 | AB | 2 | 19.10 |
| 13 | 1 | BA | 2 | 0.00 |
| 14 | 1 | BA | 2 | 80.80 |
| 15 | 1 | BA | 2 | 66.98 |
| 16 | 1 | BA | 2 | 100.00 |
| 17 | 1 | BA | 2 | 16.94 |
| 18 | 1 | BA | 2 | 100.00 |
| 19 | 1 | BA | 2 | 100.00 |
| 20 | 1 | BA | 2 | 100.00 |
| 21 | 1 | BA | 2 | 100.00 |
| 22 | 1 | BA | 2 | 75.09 |
| 23 | 1 | BA | 2 | 28.18 |
| 24 | 1 | BA | 2 | 13.07 |
Haremos un upload de los datos al sistema.
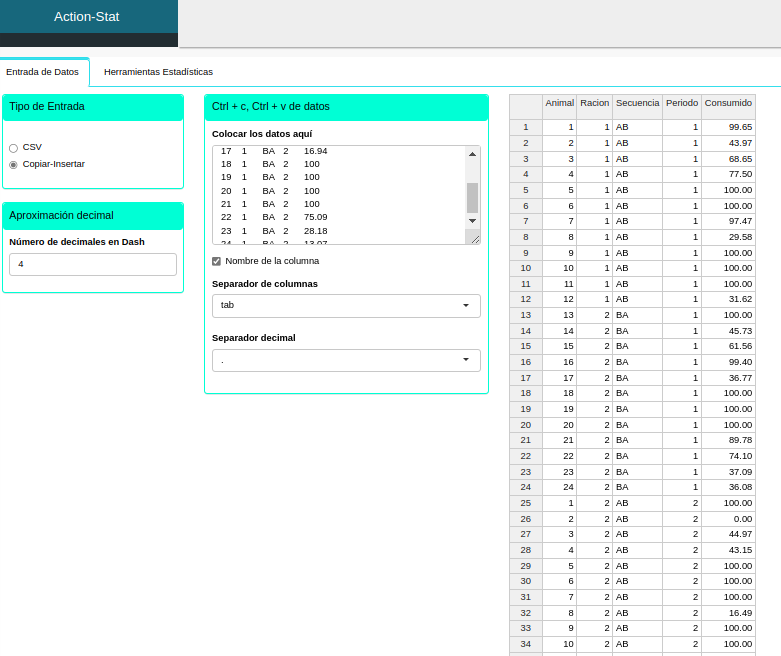
Para realizar el ANOVA de efectos mixtos, se realiza la siguiente configuración, tal y como se muestra en la siguiente figura.
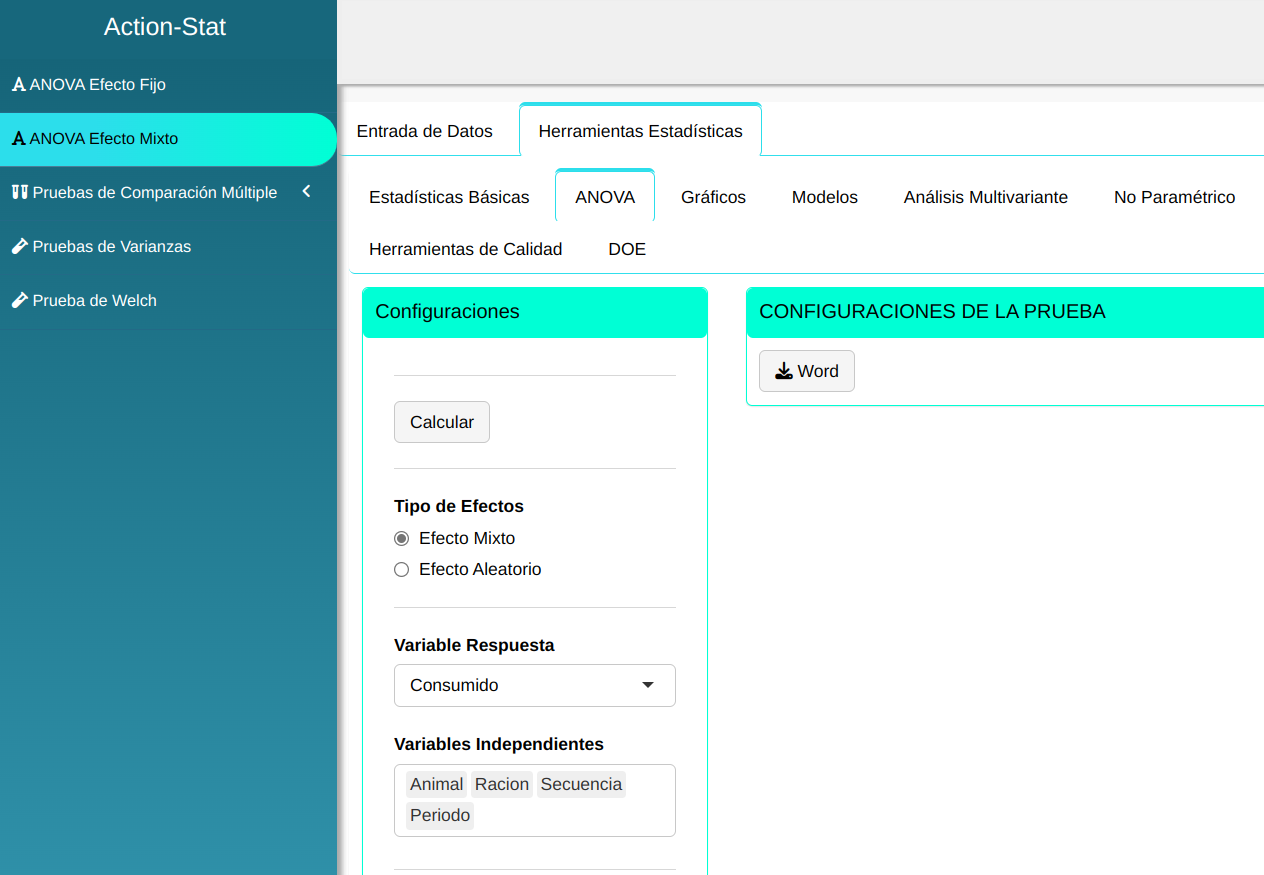
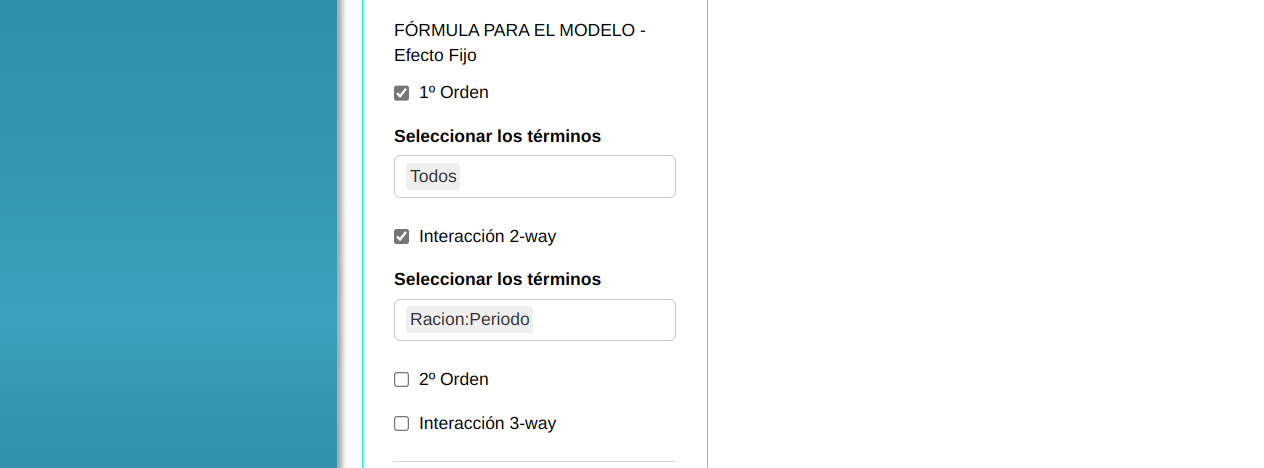
En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:
ANOVA com efecto fijo
| GL Num. | GL Den. | Suma de Cuadrados | Cuadrados Medios | Estad. F | P-valor | |
|---|---|---|---|---|---|---|
| Animal | 1 | 20 | 4.6355 | 4.6355 | 0.0143 | 0.906 |
| Ración | 1 | 30.7161 | 11.2679 | 11.2679 | 0.0348 | 0.8533 |
| Secuencia | 1 | 20.3385 | 30.252 | 30.252 | 0.0934 | 0.763 |
| Periodo | 1 | 374.6508 | 253.7175 | 253.7175 | 0.7831 | 0.3768 |
| Animal:Secuencia | 1 | 20 | 48.2699 | 48.2699 | 0.149 | 0.7036 |
| Ración:Periodo |
ANOVA con efecto aleatorio
| Factor | | Factor | Desviacón Estándar | Correlación | X² | GL | P-valor | |
|---|---|---|---|---|---|---|---|
| X | Animal | (Intercepto) | 31.1448 | 17.7508 | 1 | 0 | |
| X.1 | Ración | (Intercepto) | 1.5657 | 0.000 | 1 | 1 | |
| X.2 | Secuencia | (Intercepto) | 3.6907 | 0.000 | 1 | 1 | |
| X.3 | Periodo | (Intercepto) | 6.4968 | 0.000 | 1 | 1 | |
| X.4 | Residuos | 17.9995 |
Intervalo de confianza del Efecto Animal
| Nivel | Límite Inferior | Efecto para media | Límite Superior |
|---|---|---|---|
| 1 | 73.430 | 99.825 | 126.220 |
| 2 | -4.410 | 21.985 | 48.380 |
| 3 | 30.415 | 56.810 | 83.205 |
| 4 | 33.930 | 60.325 | 86.720 |
| 5 | 73.605 | 100.000 | 126.395 |
| 6 | 73.605 | 100.000 | 126.395 |
| 7 | 72.340 | 98.735 | 125.130 |
| 8 | -3.360 | 23.035 | 49.430 |
| 9 | 73.605 | 100.000 | 126.395 |
| 10 | 73.605 | 100.000 | 126.395 |
| 11 | 73.605 | 100.000 | 126.395 |
| 12 | -1.035 | 25.360 | 51.755 |
| 13 | 23.605 | 50.000 | 76.395 |
| 14 | 36.870 | 63.265 | 89.660 |
| 15 | 37.875 | 64.270 | 90.665 |
| 16 | 73.305 | 99.700 | 126.095 |
| 17 | 0.460 | 26.855 | 53.250 |
| 18 | 73.605 | 100.000 | 126.395 |
| 19 | 73.605 | 100.000 | 126.395 |
| 20 | 73.605 | 100.000 | 126.395 |
| 21 | 68.495 | 94.890 | 121.285 |
| 22 | 48.200 | 74.595 | 100.990 |
| 23 | 6.240 | 32.635 | 59.030 |
| 24 | -1.820 | 24.575 | 50.970 |
Intervalo de confianza del Efecto Secuencia
| Nivel | Límite Inferior | Efeto para media | Límite Superior |
|---|---|---|---|
| AB | 66.148 | 71.536 | 76.924 |
| BA | 66.148 | 71.536 | 76.924 |
Intervalo de confianza del Efecto Ración*Periodo
| Nivel | Límite Inferior | Efecto para media | Límite Superior |
|---|---|---|---|
| 1|1 | 67.401 | 76.733 | 86.065 |
| 2|1 | 66.347 | 75.680 | 85.012 |
| 1|2 | 58.060 | 67.392 | 76.724 |
| 2|2 | 57.007 | 66.339 | 75.671 |

Outliers (Cuantiles)
| Obs. | Cuantiles de la Normal | Residuos | Criterio |
|---|---|---|---|
| 13 | 2.31 | 42.312 | Banda de Confianza (Nivel de Confianza=95%) |
| 37 | -2.31 | -49.400 | Banda de Confianza (Nivel de Confianza=95%) |
| 14 | -1.62 | -23.180 | Banda de Confianza (Nivel de Confianza=95%) |
| 31 | 1.32 | 9.987 | Banda de Confianza (Nivel de Confianza=95%) |
| 4 | 1.45 | 10.234 | Banda de Confianza (Nivel de Confianza=95%) |
Prueba de Normalidad - Residuos
| Valor | |
|---|---|
| Media | 0.000 |
| Desviación Estándar | 13.091 |
| N | 48.000 |
| Anderson-Darling | 1.438 |
| P-Valor | 0.001 |
Outliers (Cuantiles)
| Obs. | Cuantiles de la Normal | Intercepto Aleatório | Criterio |
|---|---|---|---|
| 11 | 0.0500 | 20.3730 | Banda de Confianza (Nivel de Confianza=95%) |
| 20 | 2.0400 | 27.6580 | Banda de Confianza (Nivel de Confianza=95%) |
Pruebas de Normalidad - Intercepto Aleatório
| Valor | |
|---|---|
| Media | 0 |
| Desviación Estándar | 26.8847 |
| N | 24 |
| Anderson-Darling | 1.5979 |
| P-Valor | 0.0003 |
Si el valor P es menor o igual al nivel de significancia predeterminado, significa que hay una diferencia entre los dos tipos de alimento de perros ( ración ); de lo contrario, no hay diferencia.
En este caso, los P-valores son mayores que 0,05, no rechazamos la hipótesis nula de igualdad de las raciones, es decir, que las raciones no altera la cantidad de consumo animal.
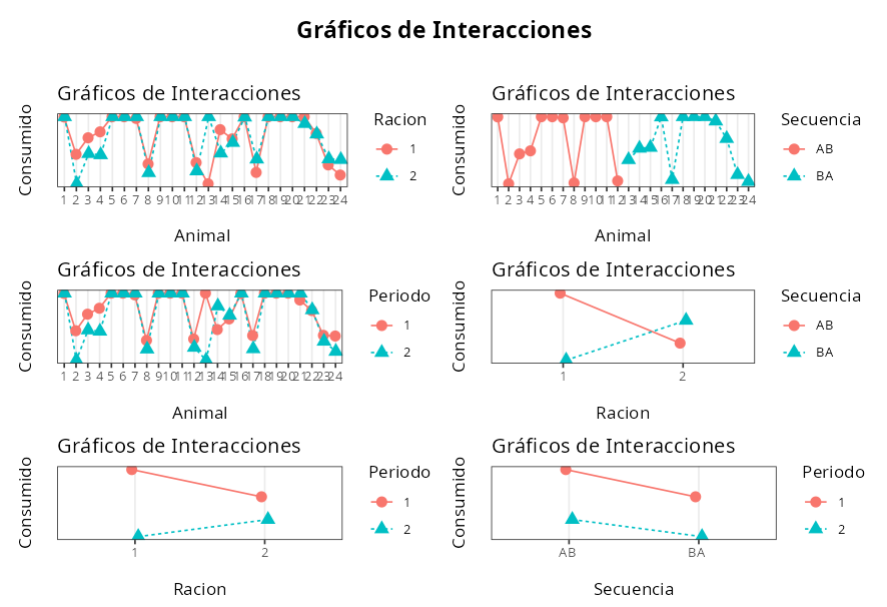
En el gráfico, los puntos negros son los promedios de cada nivel del factor, que en la tabla se denominan Efectos. Las líneas rojas representan el intervalo de confianza para las medias del nivel de factor.
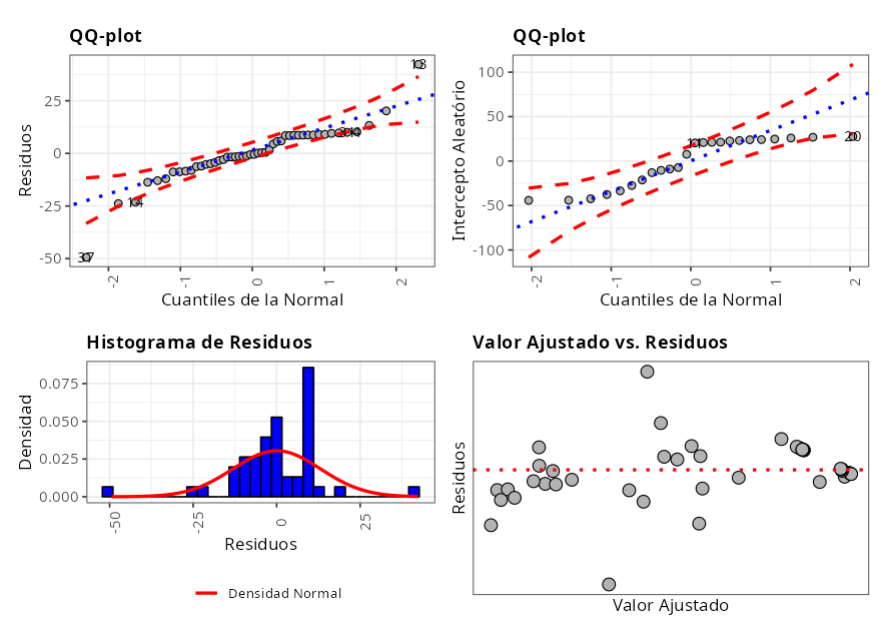
En el gráfico 1 se muestra un gráfico de Residuos versus Cuantiles Normales.
En el gráfico 2 se muestra un gráfico de intercepción aleatoria versus cuantiles normales.
En el gráfico 3 trazamos un histograma de los residuos para tener una idea de cómo se distribuyen los residuos.
En el gráfico 4 trazamos una gráfica de Residuos versus valores ajustados.
En nuestro caso usaremos la prueba de Anderson-Darling, donde la hipótesis nula es la normalidad de los datos, y por ejemplo, verificamos que no rechazamos ("aceitamos") a hipótesis nula y con esto verificamos la normalidad de los residuales y la Intercepción Aleatoria.