2. Pruebas de comparación múltiple: HSU
La estrategia HSU se utiliza para detectar el nivel con la respuesta más alta o el nivel con la respuesta más baja.
Ejemplo:
Consideremos el proceso de producción de una fibra sintética, en el que el experimentador desea conocer la influencia del porcentaje de algodón en la resistencia de la fibra. Para ello, se lleva a cabo un experimento completamente aleatorizado en el que se evalúan distintos niveles de porcentaje de algodón en relación con la resistencia de la fibra. Un punto importante en el diseño del experimento es que para cada nivel del factor (porcentaje de algodón), los demás factores que influyen en el proceso (como el medio ambiente, la máquina, la materia prima, etc.) deben presentar un patrón homogéneo de variabilidad.
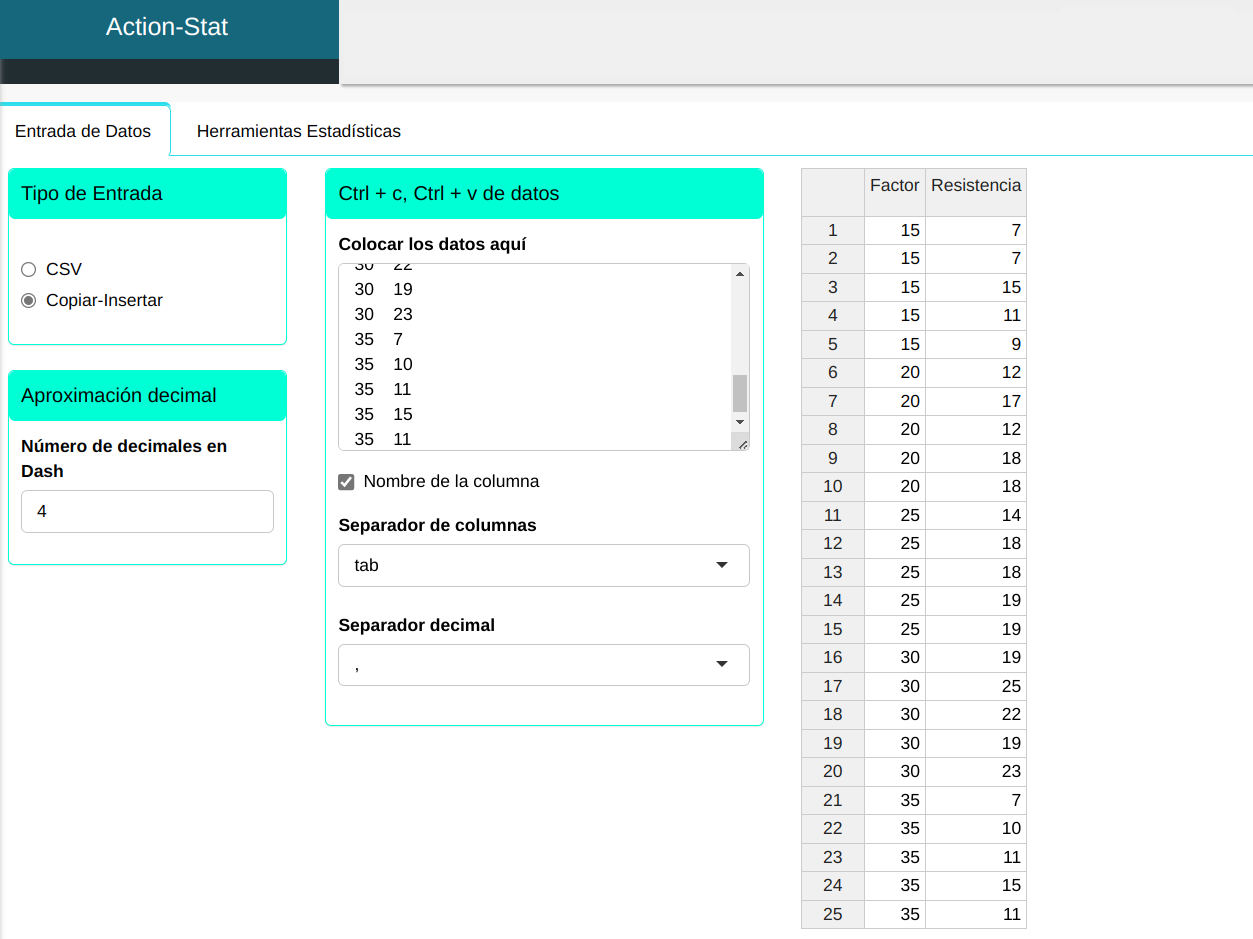
| Factor | Resistencia |
|---|---|
| 15 | 7 |
| 15 | 7 |
| 15 | 15 |
| 15 | 11 |
| 15 | 9 |
| 20 | 12 |
| 20 | 17 |
| 20 | 12 |
| 20 | 18 |
| 20 | 18 |
| 25 | 14 |
| 25 | 18 |
| 25 | 18 |
| 25 | 19 |
| 25 | 19 |
| 30 | 19 |
| 30 | 25 |
| 30 | 22 |
| 30 | 19 |
| 30 | 23 |
| 35 | 7 |
| 35 | 10 |
| 35 | 11 |
| 35 | 15 |
| 35 | 11 |
En el experimento, tomamos 5 niveles para el porcentaje de algodón y 5 réplicas.
Realizaremos la prueba HSU.
En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:
PRUEBA: Cuanto más mayor es mejor
| Nivel | Media | Límite inferior | Límite superior |
|---|---|---|---|
| 15 | -11.8 | -15.939 | 0 |
| 20 | -6.2 | -10.339 | 0 |
| 25 | -4.0 | -8.139 | 0.139 |
| 30 | 4.0 | -0.139 | 8.139 |
| 35 | -10.8 | -14.939 | 0 |
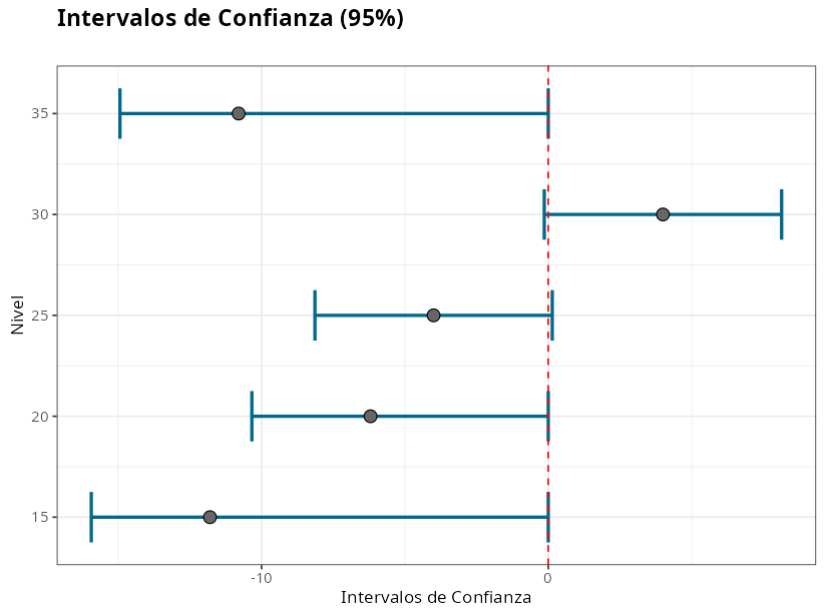
En el test HSU queremos que la mayor parte del intervalo sea positivo, por lo que el nivel 30 es el mejor si consideramos el test “la media más alta es la mejor”.