4. Pruebas de varianza
Estas pruebas evalúan la igualdad de varianza entre niveles de factores, utilizando las pruebas de Bartlet y Levene. Solo se pueden utilizar cuando existe un único factor. Esta herramienta también genera la gráfica de los intervalos de confianza para la desviación estándar.
Ejemplo 1:
Consideremos el proceso de producción de una fibra sintética, en el que el experimentador desea conocer la influencia del porcentaje de algodón en la resistencia de la fibra. Para ello, se lleva a cabo un experimento completamente aleatorizado en el que se evalúan distintos niveles de porcentaje de algodón en relación con la resistencia de la fibra. Un punto importante en el diseño del experimento es que para cada nivel del factor (porcentaje de algodón), los demás factores que influyen en el proceso (como el medio ambiente, la máquina, la materia prima, etc.) deben presentar un patrón homogéneo de variabilidad.
En el experimento, tomamos 5 niveles para el porcentaje de algodón y 5 réplicas.
| Factor | Resistencia |
|---|---|
| 15 | 7 |
| 15 | 7 |
| 15 | 15 |
| 15 | 11 |
| 15 | 9 |
| 20 | 12 |
| 20 | 17 |
| 20 | 12 |
| 20 | 18 |
| 20 | 18 |
| 25 | 14 |
| 25 | 18 |
| 25 | 18 |
| 25 | 19 |
| 25 | 19 |
| 30 | 19 |
| 30 | 25 |
| 30 | 22 |
| 30 | 19 |
| 30 | 23 |
| 35 | 7 |
| 35 | 10 |
| 35 | 11 |
| 35 | 15 |
| 35 | 11 |
Para realizar la prueba de varianza, se elabora la siguiente configuración que se muestra en la figura siguiente.
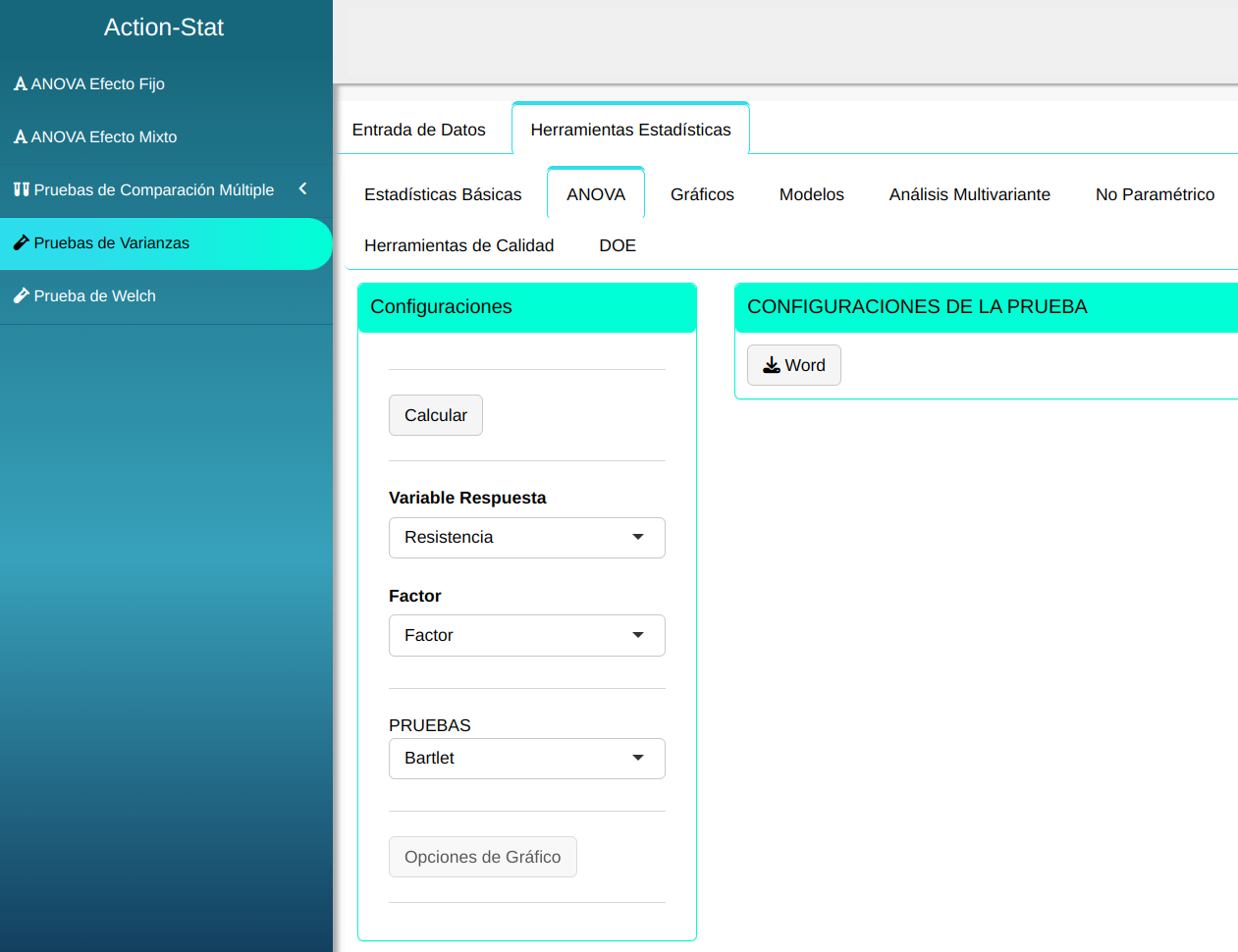
En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:
Prueba de varianza
| Información | Valor |
|---|---|
| Bartlett (estadística de prueba) | 0.933 |
| Grados de libertad | 4.000 |
| P-valor | 0.920 |
Intervalos de confianza para la desviación estándar
| Factor | Límite inferior | Desviación Estándar | Límite superior |
|---|---|---|---|
| 15 | 1.736 | 3.347 | 14.712 |
| 20 | 1.624 | 3.130 | 13.762 |
| 25 | 1.076 | 2.074 | 9.116 |
| 30 | 1.353 | 2.608 | 11.463 |
| 35 | 1.486 | 2.864 | 12.588 |
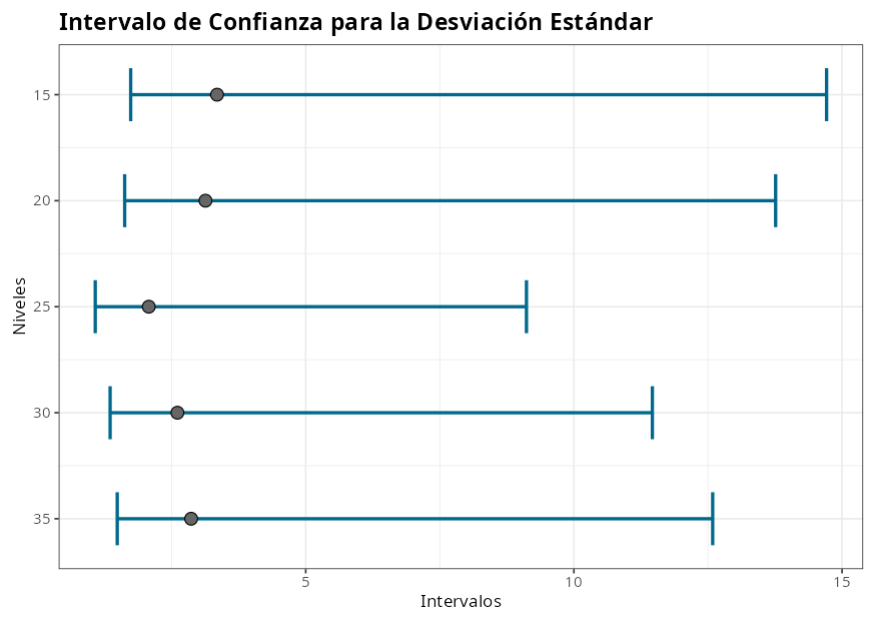
Verificamos que el P-valor de la prueba es mayor que el nivel de significancia elegido el 5%, por lo tanto no rechazamos la hipótesis de igualdad de las varianzas.
Ejemplo 2:
Con los mismos datos del Ejemplo 1, ahora aplicaremos el Test de Levene.
| Factor | Resistencia |
|---|---|
| 15 | 7 |
| 15 | 7 |
| 15 | 15 |
| 15 | 11 |
| 15 | 9 |
| 20 | 12 |
| 20 | 17 |
| 20 | 12 |
| 20 | 18 |
| 20 | 18 |
| 25 | 14 |
| 25 | 18 |
| 25 | 18 |
| 25 | 19 |
| 25 | 19 |
| 30 | 19 |
| 30 | 25 |
| 30 | 22 |
| 30 | 19 |
| 30 | 23 |
| 35 | 7 |
| 35 | 10 |
| 35 | 11 |
| 35 | 15 |
| 35 | 11 |
Para realizar la prueba de varianza, se elabora la siguiente configuración que se muestra en la figura siguiente.
En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:
Prueba de varianza
| Información | Valor |
|---|---|
| Levene (estadística de prueba) | 0.318 |
| Grados de libertad | 4.000 |
| P-valor | 0.863 |
Intervalos de confianza para la desviación estándar
| Factor | Límite inferior | Desviación estándar | Límite superior |
|---|---|---|---|
| 15 | 1.736 | 3.347 | 14.712 |
| 20 | 1.624 | 3.130 | 13.762 |
| 25 | 1.076 | 2.074 | 9.116 |
| 30 | 1.353 | 2.608 | 11.463 |
| 35 | 1.486 | 2.864 | 12.588 |
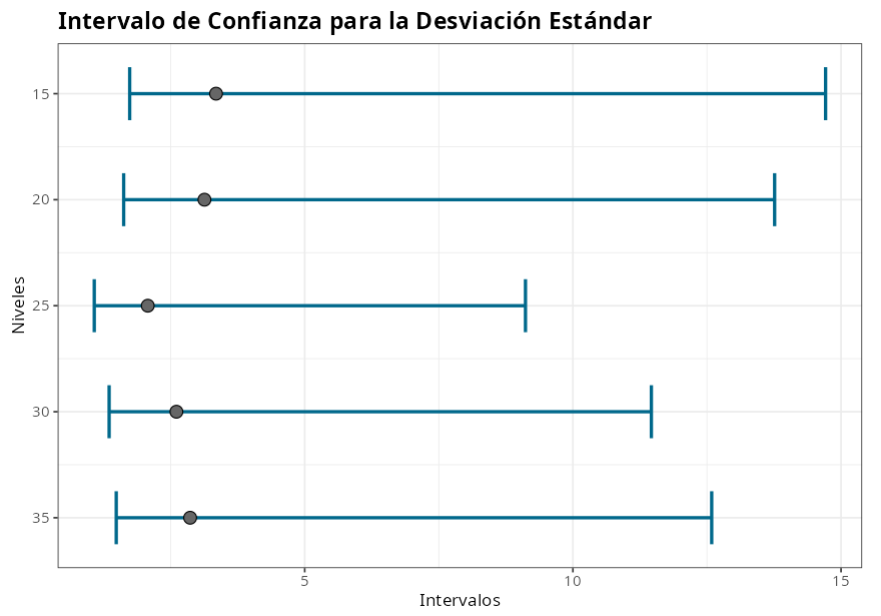
Comprobamos que el P-valor del test es mayor que el nivel de significancia elegido el 5%, por lo tanto no rechazamos la hipótesis de igualdad de varianzas.