5. Prueba de Welch
La prueba de Welch se utiliza para evaluar la importancia entre la diferencia de los promedios observados.
Ejemplo:
Consideremos un proceso, producto o servicio en el que deseamos evaluar el impacto del factor A, de modo que A tenga k niveles, siendo estos niveles fijos. Consideremos que se selecciona aleatoriamente una muestra de N unidades experimentales de una población de unidades experimentales. La unidad experimental es la unidad básica a la que se aplican los tratamientos.
| Factor | Resistencia |
|---|---|
| 15 | 7 |
| 15 | 7 |
| 15 | 15 |
| 15 | 11 |
| 15 | 9 |
| 20 | 12 |
| 20 | 17 |
| 20 | 12 |
| 20 | 18 |
| 20 | 18 |
| 25 | 14 |
| 25 | 18 |
| 25 | 18 |
| 25 | 19 |
| 25 | 19 |
| 30 | 19 |
| 30 | 25 |
| 30 | 22 |
| 30 | 19 |
| 30 | 23 |
| 35 | 7 |
| 35 | 10 |
| 35 | 11 |
| 35 | 15 |
| 35 | 11 |
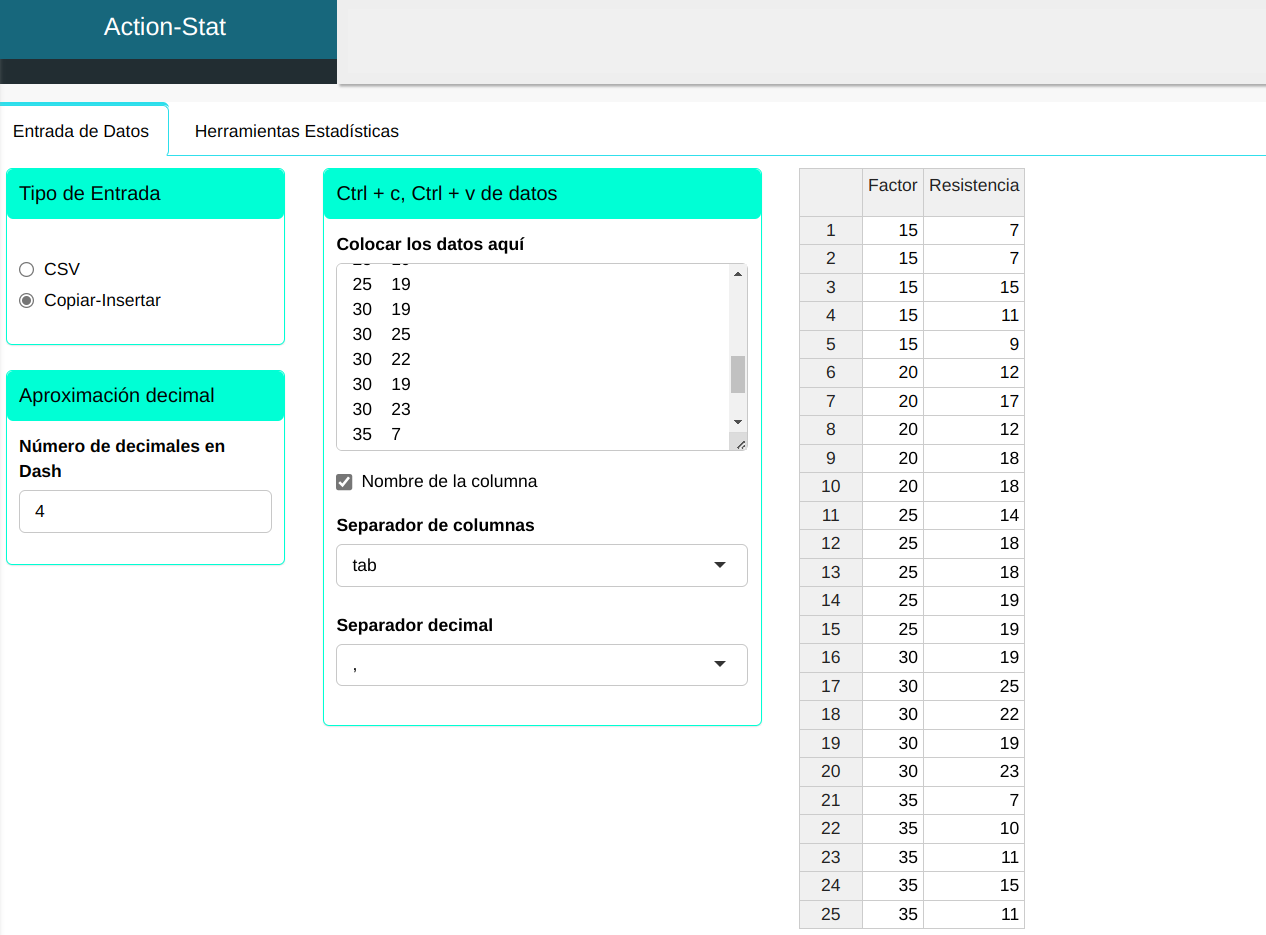
Haremos el test de Welch:
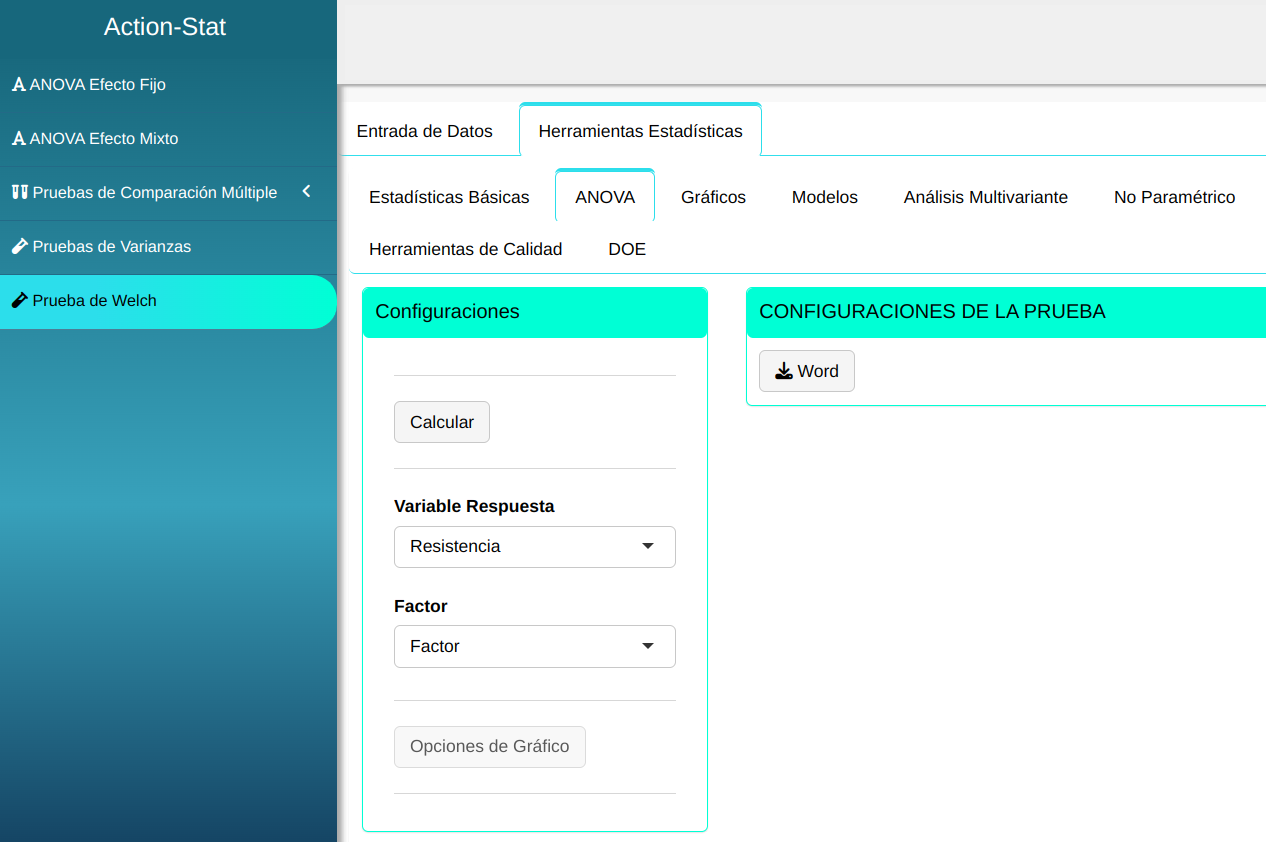
En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:
Prueba de Welch (Modelo Heterocedástico)
Tabla 1: Prueba de Welch (modelo heteroscedástico)
| Estad. F | GL Núm. | GL Denomi | P-valor | |
|---|---|---|---|---|
| F | 12.451 | 4 | 9.916 | 0.000698745 |
Intervalo de confianza de las Medias
| Factor | Media | Desviación estándar | Límite inferior | Límite superior |
|---|---|---|---|---|
| 15 | 9.8 | 3.347 | 5.645 | 13.955 |
| 20 | 15.4 | 3.130 | 11.513 | 19.287 |
| 25 | 17.6 | 2.074 | 15.025 | 20.175 |
| 30 | 21.6 | 2.608 | 18.362 | 24.838 |
| 35 | 10.8 | 2.864 | 7.244 | 14.356 |
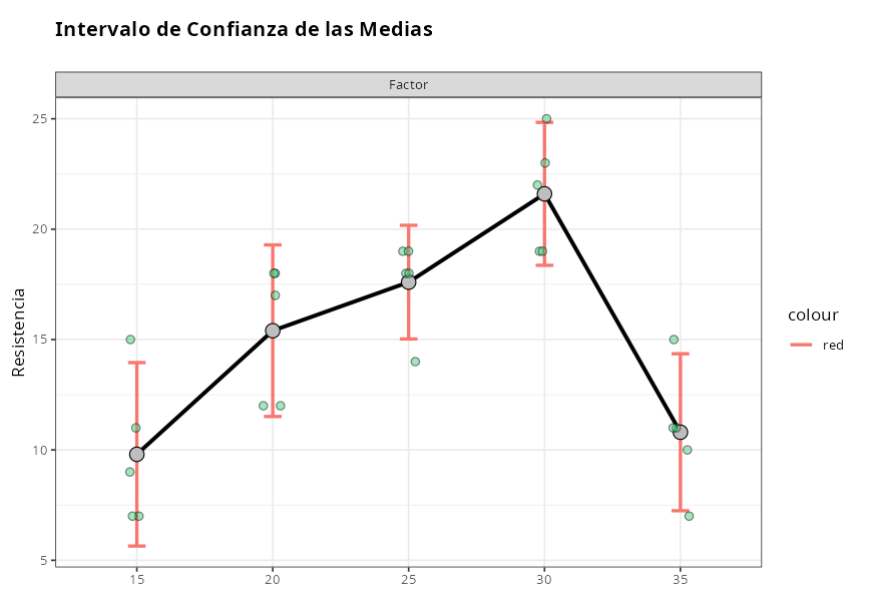
Como el P-valor = 0.000698745, rechazamos la hipótesis H0, es decir, para un nivel de significancia del 5% tenemos evidencia de que las medias no son iguales. El gráfico anterior nos ayudan a llegar a esta conclusión.
En el gráfico muestra el promedio de cada nivel y los respectivos intervalos de confianza.