3. Cubos
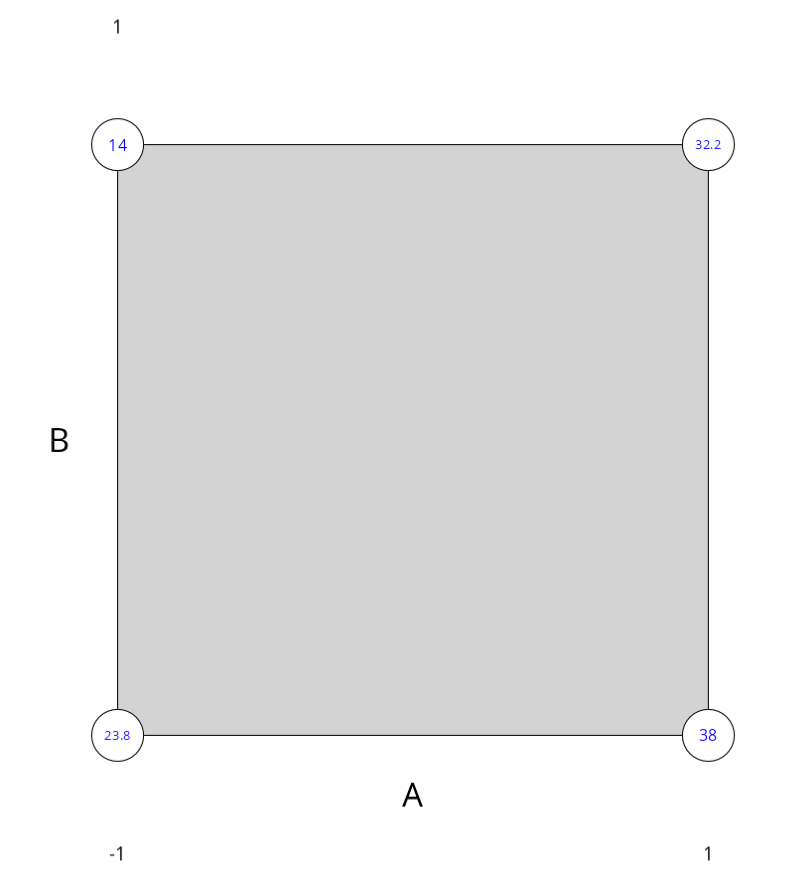
El gráfico cúbico se utiliza para identificar visualmente las posibles soluciones del experimento.
Ejemplo 1:
El gráfico de cubos se utiliza para identificar visualmente las posibles soluciones del experimento.
Proceso de pegar un circuito integrado a una base.
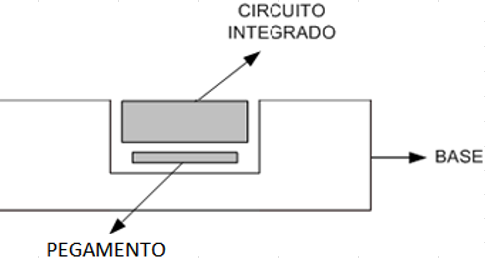
La siguiente tabla resume las condiciones del experimento.
| Variables de Respuesta | Y: Fuerza del pegamento (libras) |
|---|---|
| A: Tipo de pegamento (niveles $A_{-1}$:marca actual y $A_{+1}$: nueva marca) | |
| Factores | B : Material de la base (niveles $B_{-1}$: actual y $B_{+1}$: Nueva Especificación) |
| C: Tiempo de curado a $100ºC$ (niveles $C_{-1}$: 90 min y $C_{+1}$: 120 min) | |
| Nro. de tratamientos: | $2^3=8$ |
| Nro. de réplicas: | 2 |
| Nro. de carreras: | $8*2=16$ |
Los datos observados del experimento (completo) con 2 repeticiones se dan a continuación, con el orden aleatorio de ejecución entre paréntesis.
Construiremos una tabla como la siguiente:
| Tratamiento | A | B | C | Y |
|---|---|---|---|---|
| 0 | -1 | -1 | -1 | 82,9 |
| a | 1 | -1 | -1 | 95 |
| c | -1 | 1 | -1 | 80 |
| ab | 1 | 1 | -1 | 105 |
| c | -1 | -1 | 1 | 93,1 |
| ac | 1 | -1 | 1 | 104 |
| bc | -1 | 1 | 1 | 89,7 |
| abc | 1 | 1 | 1 | 114 |
| 0 | -1 | -1 | -1 | 88,6 |
| a | 1 | -1 | -1 | 96,4 |
| b | -1 | 1 | -1 | 78,6 |
| ab | 1 | 1 | -1 | 103,6 |
| c | -1 | -1 | 1 | 94,7 |
| ac | 1 | -1 | 1 | 101,2 |
| bc | -1 | 1 | 1 | 86,9 |
| abc | 1 | 1 | 1 | 111,8 |
Subiremos los datos al sistema.
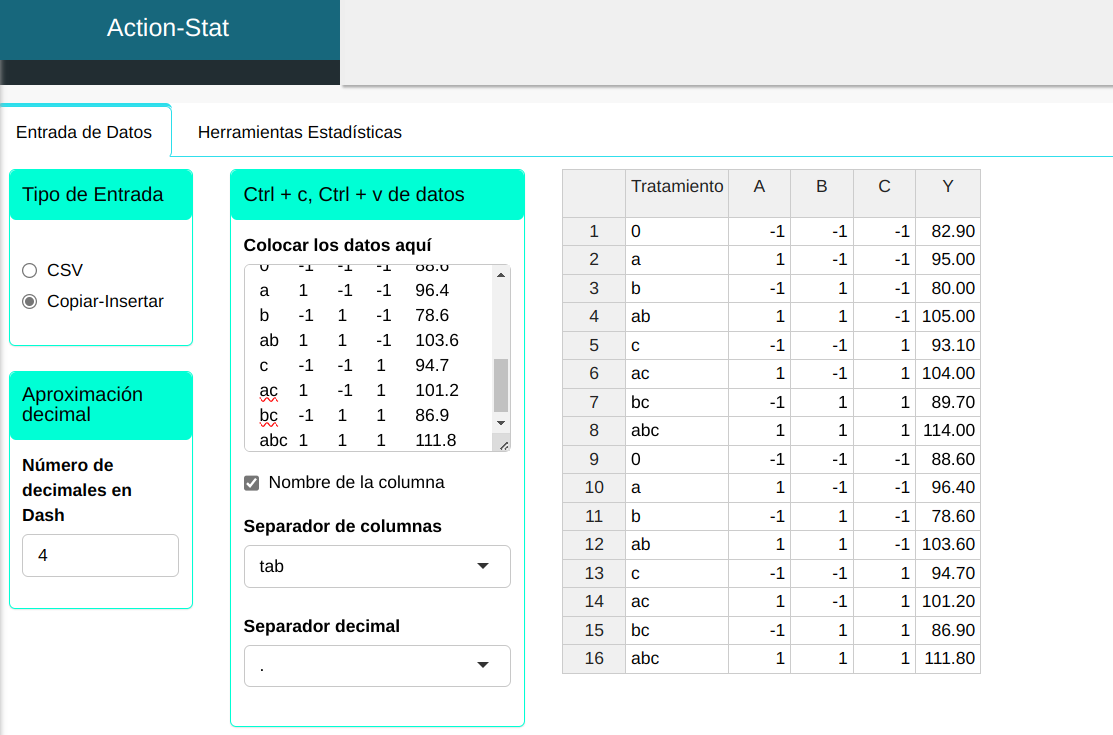
Realizaremos el análisis. Para ello basta acceder a DOE e seleccionamos las opciones conforme la figura de abajo.
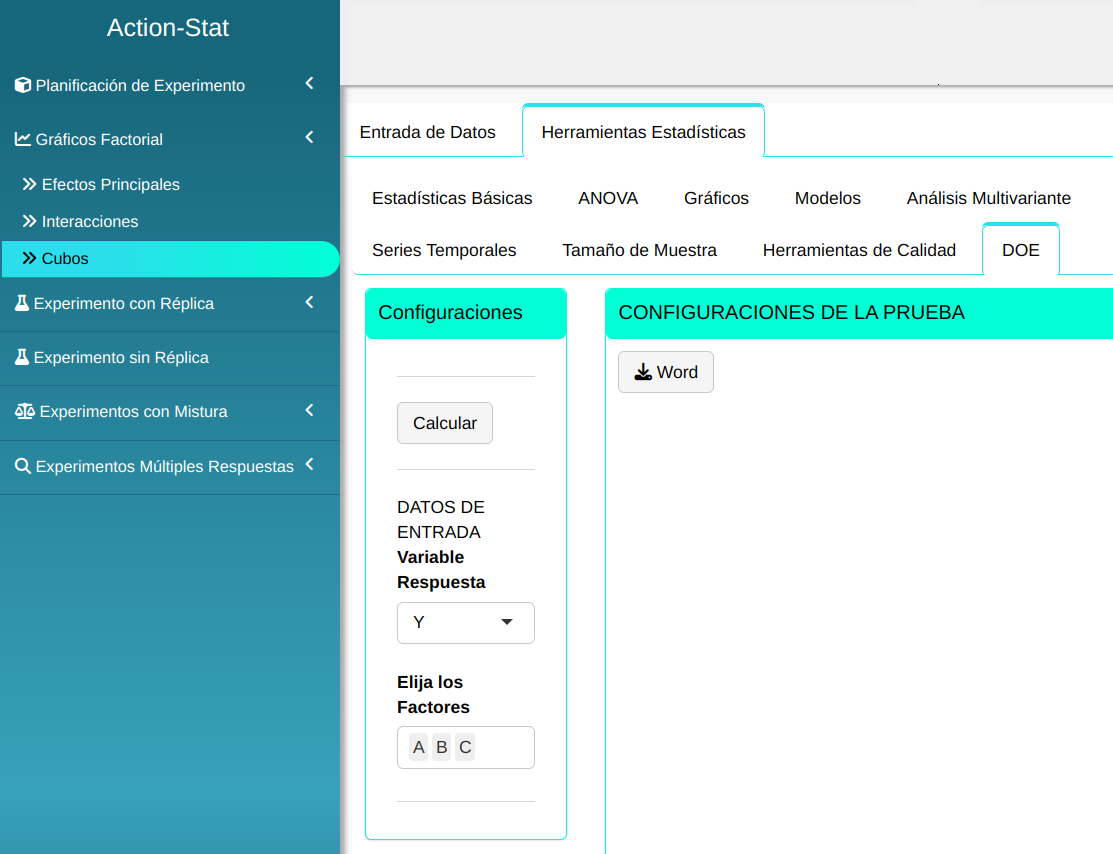
En seguida, haga un clic en Calcular para obtener los resultados.
Los resultados son:
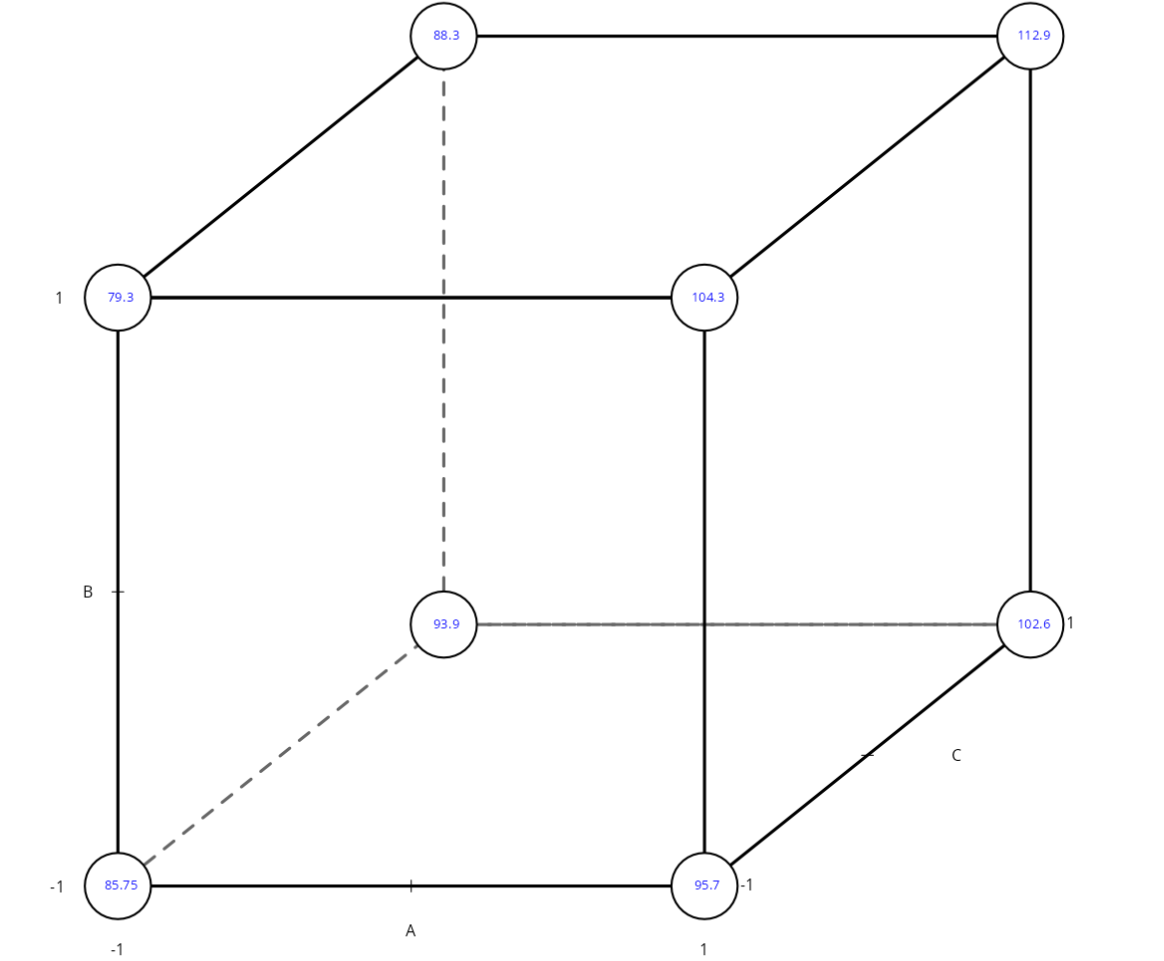
Medias de los Valores
| A | B | C | Y | |
|---|---|---|---|---|
| 1 | -1 | -1 | -1 | 85.75 |
| 2 | 1 | -1 | -1 | 95.70 |
| 3 | -1 | -1 | 1 | 93.90 |
| 4 | 1 | -1 | 1 | 102.60 |
| 5 | -1 | 1 | -1 | 79.30 |
| 6 | 1 | 1 | -1 | 104.30 |
| 7 | -1 | 1 | 1 | 88.30 |
| 8 | 1 | 1 | 1 | 112.90 |
Ejemplo 2:
Estudiar el efecto en el tiempo de una determinada reacción química con variación en la temperatura y concentración de un reactivo, tal como se representa a continuación.

Para el ejemplo anterior, podemos definir:
| Variável de resposta | Y: Tempo de reação |
|---|---|
| Factores | A: Concentración de Reactivo (Níveis $V_{-1}$=10% e $V_{+1}$=20%) |
| B: Temperatura (Niveles $T_{-1}$=80ºC e $T_{+1}$=90ºC) | |
| Tratamientos | $V_{-1}$ $T_{-1}$ - concentración a 10% e temperatura a 80ºC ((0)),$\quad$ & |
| $V_{+1}$ $T_{-1}$ - concentración en 20% y temperatura a 80ºC (a), | |
| $V_{-1}$ $T_{+1}$ - concentración en 10% y temperatura a 90ºC (b) | |
| $V_{+1}$ $T_{+1}$ - concentración en 20% y temperatura a 90ºC (ab) | |
| (El número de tratamientos es 2k, en este caso $2^2$=4) | |
| Unidad Experimental | Período de tiempo para cada reacción |
| Réplicas | Repeticiones del experimento bajo las mismas condiciones experimentales, |
| como en el caso del ejemplo com el mismo nivel de temperatura y | |
| reactivo. Cuanto más réplicas haya, los resultados del experimento serán | |
| más confiables. |
–
Construye una tabla como la siguiente:
| Tratamiento | A | B | Y |
|---|---|---|---|
| 0 | -1 | -1 | 26,6 |
| (a) | 1 | -1 | 40,9 |
| (b) | -1 | 1 | 11,8 |
| (ab) | 1 | 1 | 34 |
| 0 | -1 | -1 | 22 |
| (a) | 1 | -1 | 36,4 |
| (b) | -1 | 1 | 15,9 |
| (ab) | 1 | 1 | 29 |
| 0 | -1 | -1 | 22,8 |
| (a) | 1 | -1 | 36,7 |
| (b) | -1 | 1 | 14,3 |
| (ab) | 1 | 1 | 33,6 |
Subiremos los datos al sistema.
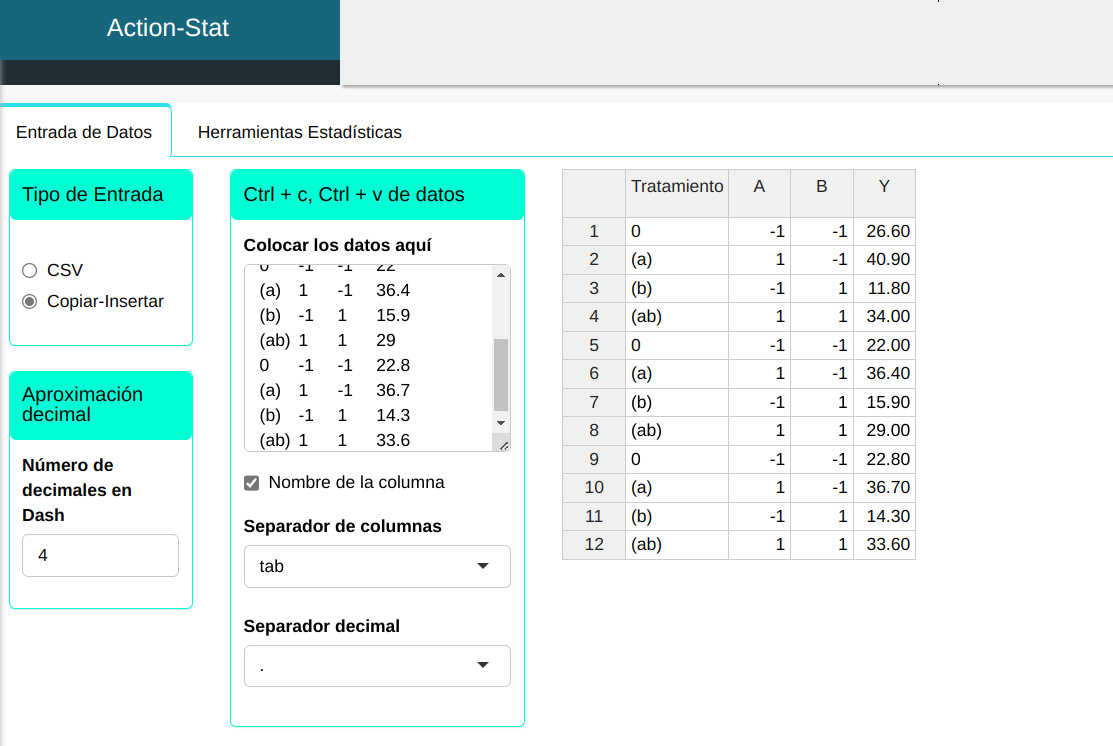
Haremos la gráfica del cubo.
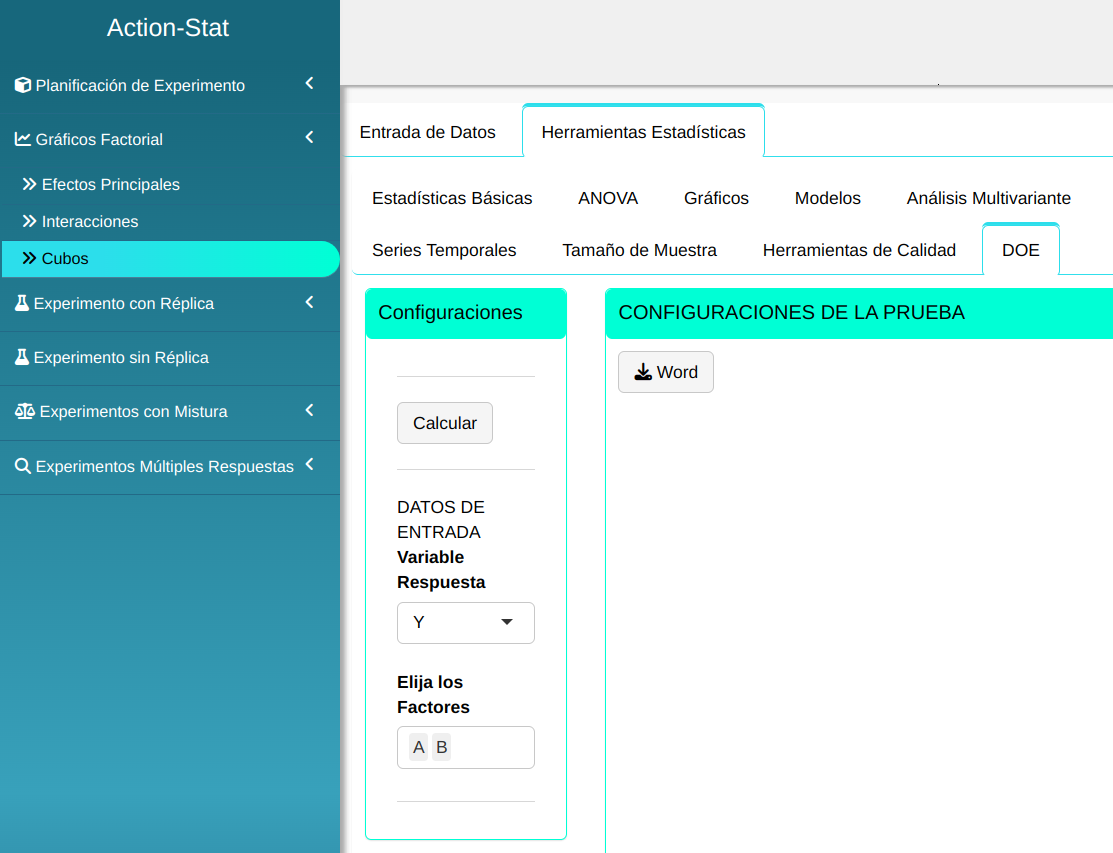
Clicando en Calcular obtenemos los resultados.
Los resultados son:
Medias de los Valores
| A | B | Y | |
|---|---|---|---|
| 1 | -1 | -1 | 23.8 |
| 2 | 1 | -1 | 38.0 |
| 3 | -1 | 1 | 14.0 |
| 4 | 1 | 1 | 32.2 |
Gráfico de media de respuesta