15. Distribuciones
La herramienta Distribuciones de Action calcula la densidad, el cuantil y el percentil de varias distribuciones continuas y discretas.
Ejemplo 1:
Considera X una variable aleatoria Normal con media 11.15 y desviación típica 2.238. Calcule la densidad de probabilidad.
| 7.57 |
| 12.29 |
| 10.35 |
| 16.28 |
| 11.79 |
| 10.17 |
| 10.77 |
| 11.27 |
| 7.39 |
| 8.25 |
| 8.39 |
| 12.27 |
| 12.82 |
| 12.26 |
| 12.07 |
| 9.72 |
| 8.45 |
| 8.67 |
| 11.17 |
| 8.40 |
| 11.92 |
| 9.39 |
| 9.62 |
| 18.53 |
| 11.67 |
| 8.75 |
| 9.63 |
| 13.06 |
| 4.69 |
| 12.43 |
| 7.69 |
| 10.64 |
| 10.55 |
| 8.85 |
| 6.02 |
| 8.88 |
| 15.46 |
| 12.79 |
| 11.27 |
| 8.01 |
| 9.69 |
| 9.91 |
| 8.43 |
| 12.88 |
| 11.50 |
| 9.82 |
| 14.55 |
| 9.88 |
| 13.25 |
| 10.35 |
Subiremos los datos al sistema.
Para calcular la densidad de probabilidad, se realiza la siguiente configuración como se muestra en la siguiente figura.
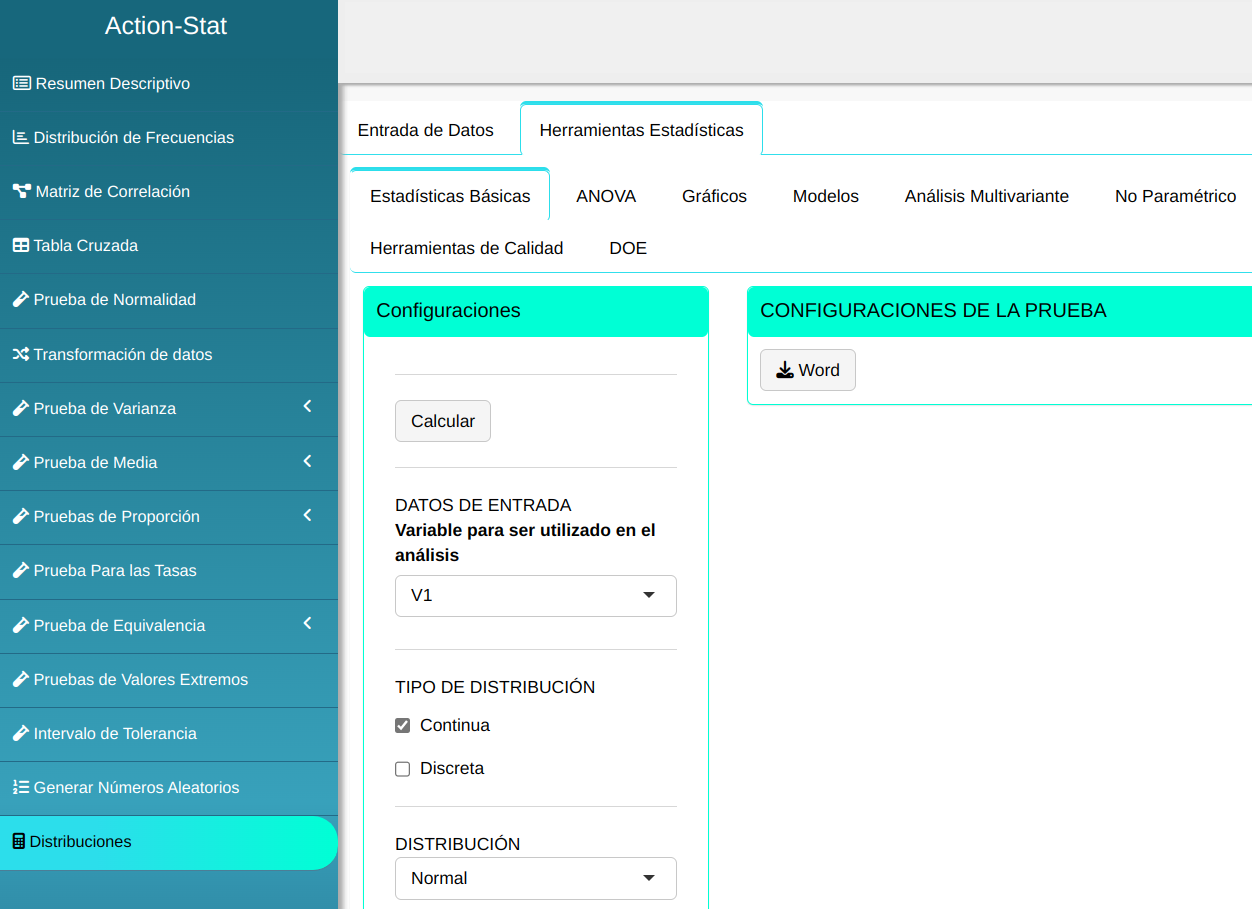
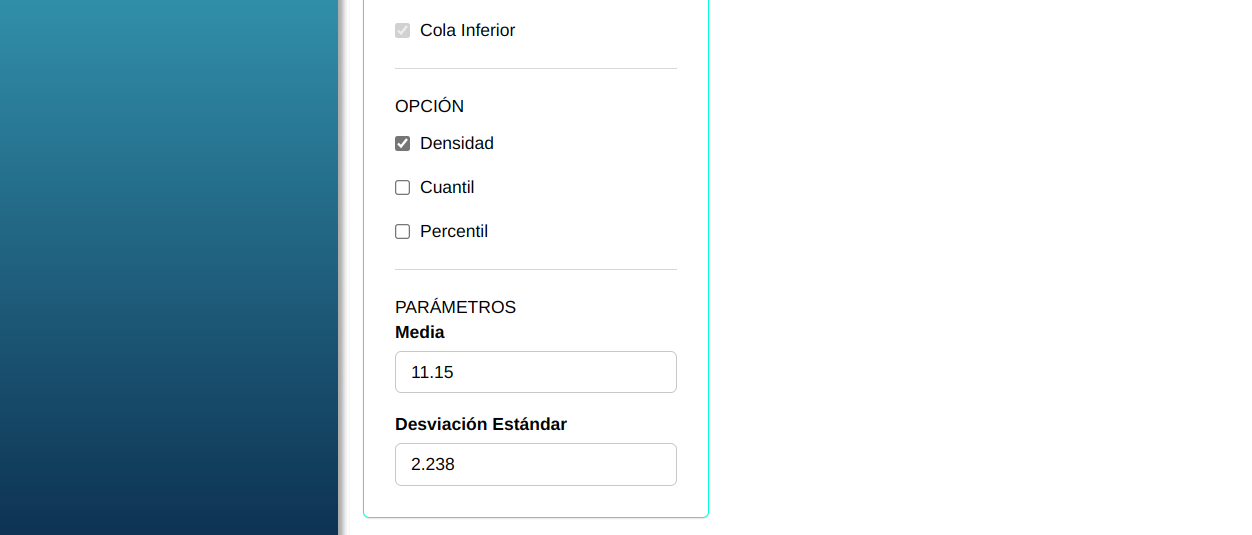
En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:
| Resultados |
|---|
| 0.050 |
| 0.157 |
| 0.167 |
| 0.013 |
| 0.171 |
| 0.162 |
| 0.176 |
| 0.178 |
| 0.044 |
| 0.077 |
| 0.083 |
| 0.157 |
| 0.135 |
| 0.157 |
| 0.164 |
| 0.145 |
| 0.086 |
| 0.097 |
| 0.178 |
| 0.084 |
| 0.168 |
| 0.131 |
| 0.141 |
| 0.001 |
| 0.174 |
| 0.100 |
| 0.141 |
| 0.124 |
| 0.003 |
| 0.151 |
| 0.054 |
| 0.174 |
| 0.172 |
| 0.105 |
| 0.013 |
| 0.106 |
| 0.028 |
| 0.136 |
| 0.178 |
| 0.066 |
| 0.144 |
| 0.153 |
| 0.085 |
| 0.132 |
| 0.176 |
| 0.150 |
| 0.056 |
| 0.152 |
| 0.115 |
| 0.167 |
Ejemplo 2:
Considere X una variable aleatoria normal con media 11.15 y desviación estándar de 2.238. Calculemos ciertos percentiles de esta distribución.
| V1 |
|---|
| 7.57 |
| 12.29 |
| 10.35 |
| 16.28 |
| 11.79 |
| 10.17 |
| 10.77 |
| 11.27 |
| 7.39 |
| 8.25 |
| 8.39 |
| 12.27 |
| 12.82 |
| 12.26 |
| 12.07 |
| 9.72 |
| 8.45 |
| 8.67 |
| 11.17 |
| 8.4 |
| 11.92 |
| 9.39 |
| 9.62 |
| 18.53 |
| 11.67 |
| 8.75 |
| 9.63 |
| 13.06 |
| 4.69 |
| 12.43 |
| 7.69 |
| 10.64 |
| 10.55 |
| 8.85 |
| 6.02 |
| 8.88 |
| 15.46 |
| 12.79 |
| 11.27 |
| 8.01 |
| 9.69 |
| 9.91 |
| 8.43 |
| 12.88 |
| 11.5 |
| 9.82 |
| 14.55 |
| 9.88 |
| 13.25 |
| 10.35 |
Subiremos los datos al sistema.
Para calcular los percentiles, se realiza la siguiente configuración como se muestra en la siguiente figura.
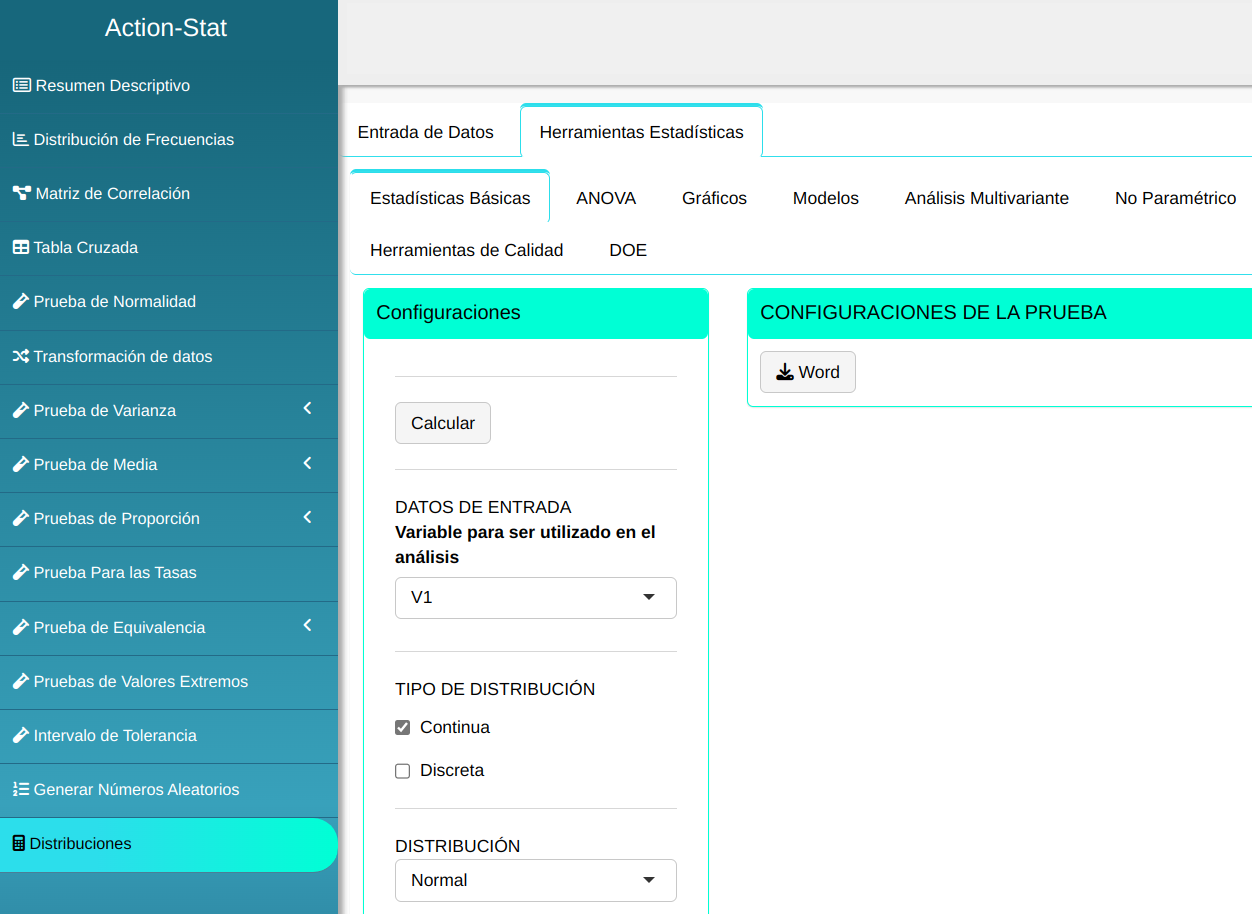
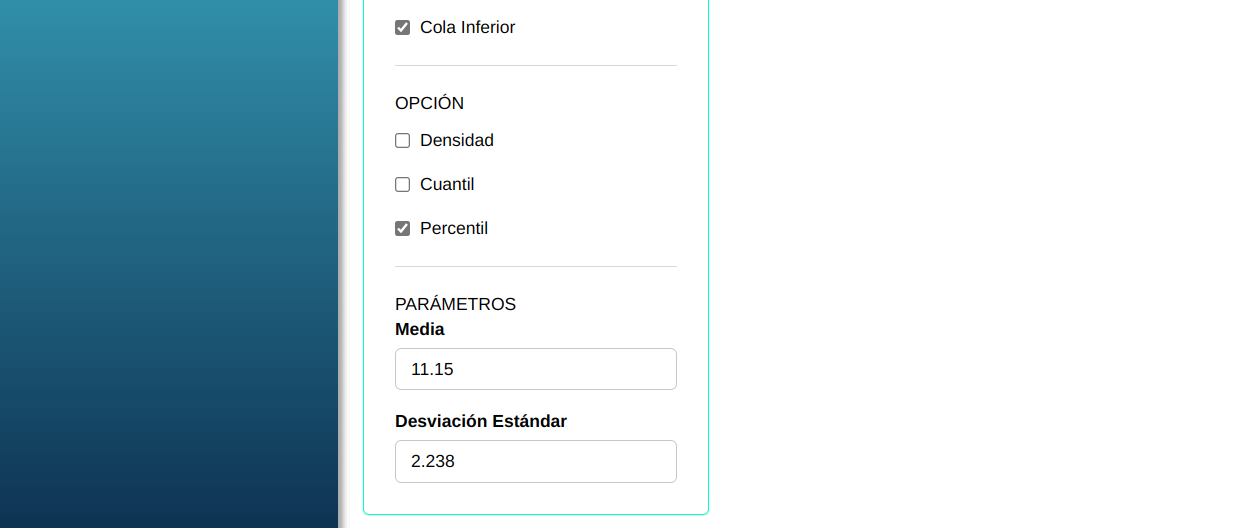
En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:
| Resultados |
|---|
| 0.055 |
| 0.695 |
| 0.360 |
| 0.989 |
| 0.612 |
| 0.331 |
| 0.432 |
| 0.522 |
| 0.047 |
| 0.097 |
| 0.109 |
| 0.692 |
| 0.772 |
| 0.691 |
| 0.659 |
| 0.262 |
| 0.114 |
| 0.134 |
| 0.504 |
| 0.109 |
| 0.634 |
| 0.215 |
| 0.247 |
| 1.000 |
| 0.591 |
| 0.142 |
| 0.248 |
| 0.804 |
| 0.002 |
| 0.716 |
| 0.061 |
| 0.411 |
| 0.394 |
| 0.152 |
| 0.011 |
| 0.155 |
| 0.973 |
| 0.768 |
| 0.521 |
| 0.080 |
| 0.257 |
| 0.289 |
| 0.112 |
| 0.780 |
| 0.562 |
| 0.277 |
| 0.936 |
| 0.285 |
| 0.826 |
| 0.360 |
Ejemplo 3:
Considere X una variable aleatoria normal con media 11.15 y desviación norma 2.238. Calculemos ciertos cuantiles de esta distribución.
Primero digitaremos las probabilidades a partir de las cuales queremos hallar los cuantiles de la distribución de interés.
Subiremos los datos al sistema.
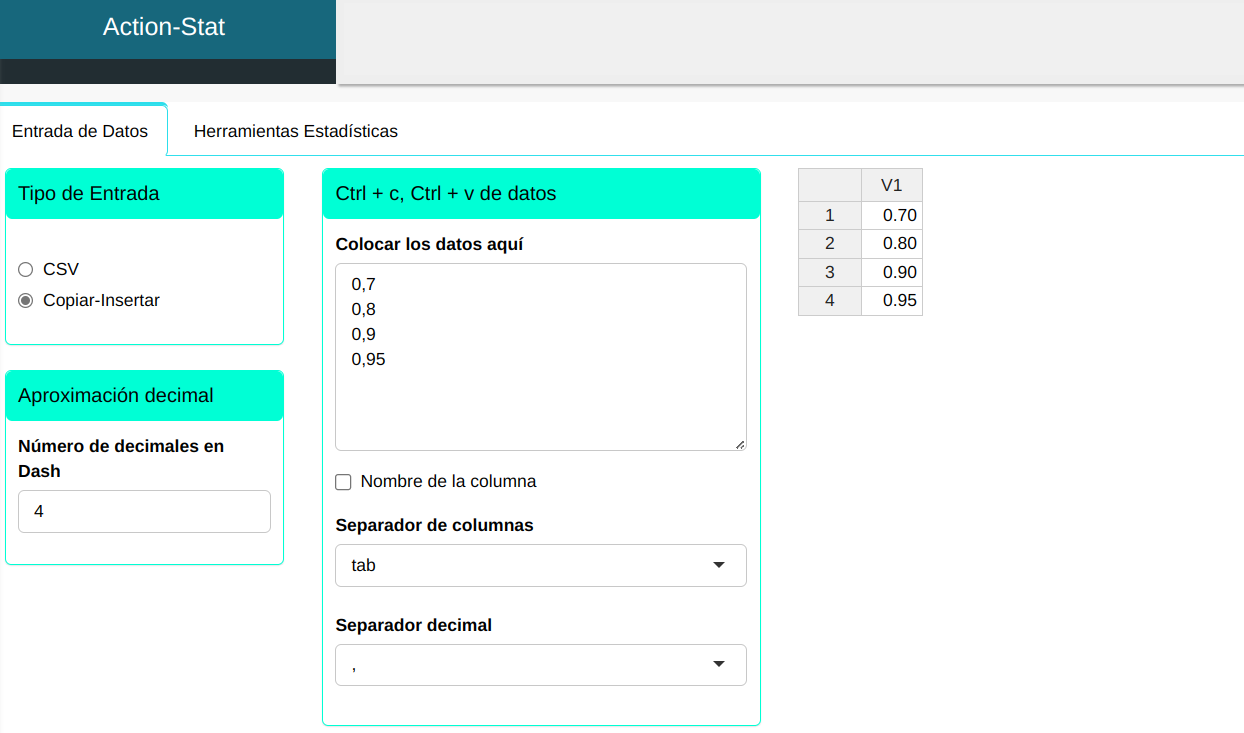
Para calcular los cuantiles, se realiza la siguiente configuración como se muestra en la siguiente figura.
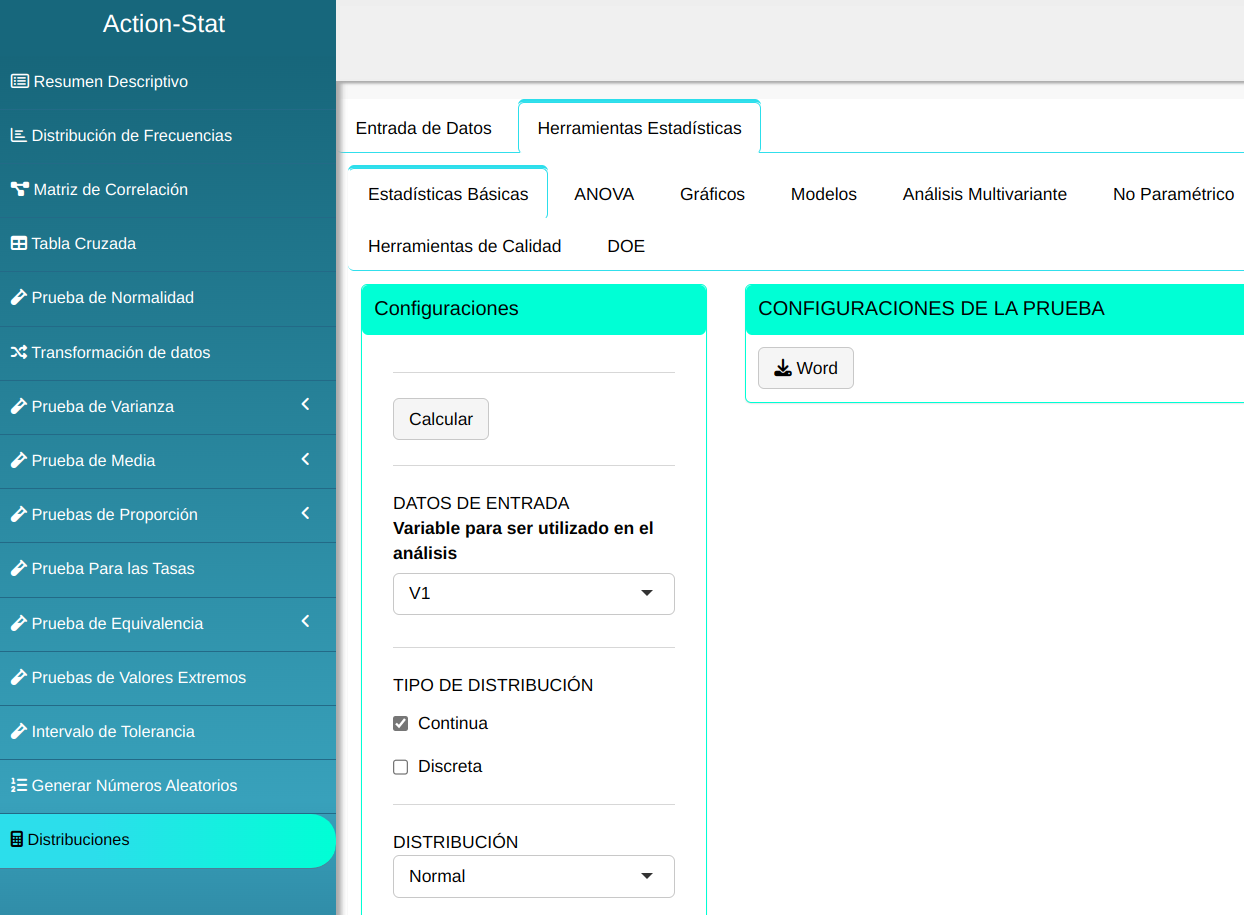
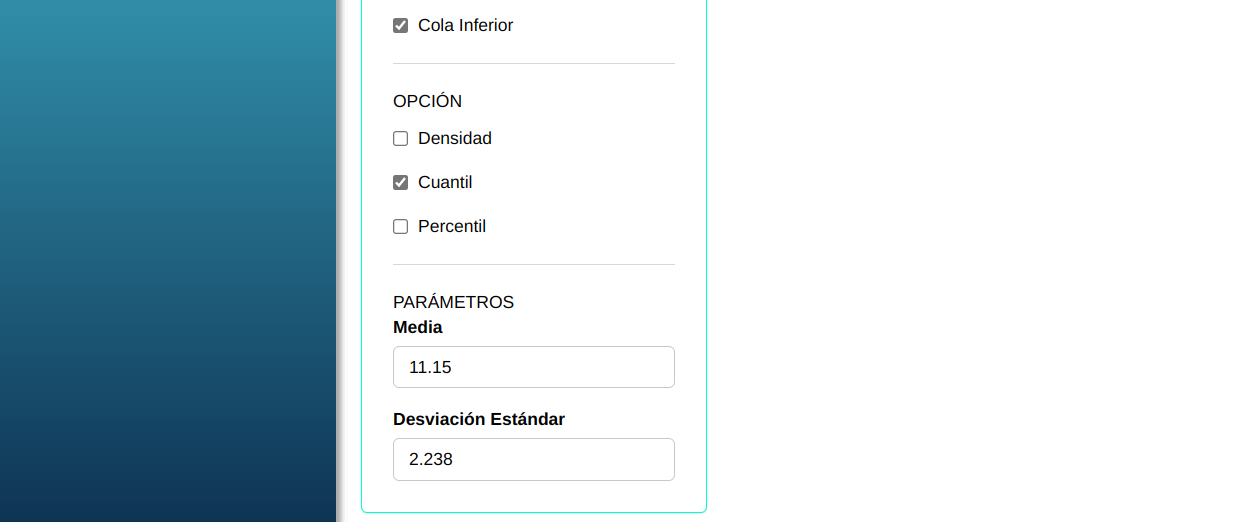
En seguida. haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:
| Resultados |
|---|
| 12.32361 |
| 13.03355 |
| 14.01811 |
| 14.83118 |
Ejemplo 4:
Supongamos que en una línea de producción la probabilidad de obtener una pieza defectuosa (éxito) es p=0.1. Se toma una muestra de 4 piezas para inspeccionarlas. ¿Cuál es la probabilidad de obtener una pieza defectuosa. ninguna pieza defectuosa. 2 piezas defectuosas. 3 y 4 piezas defectuosas?
Primero vamos a digitar los posibles valores que puede asumir la variable aleatoria. en este caso sería la cantidad de piezas que pueden estar defectuosas.
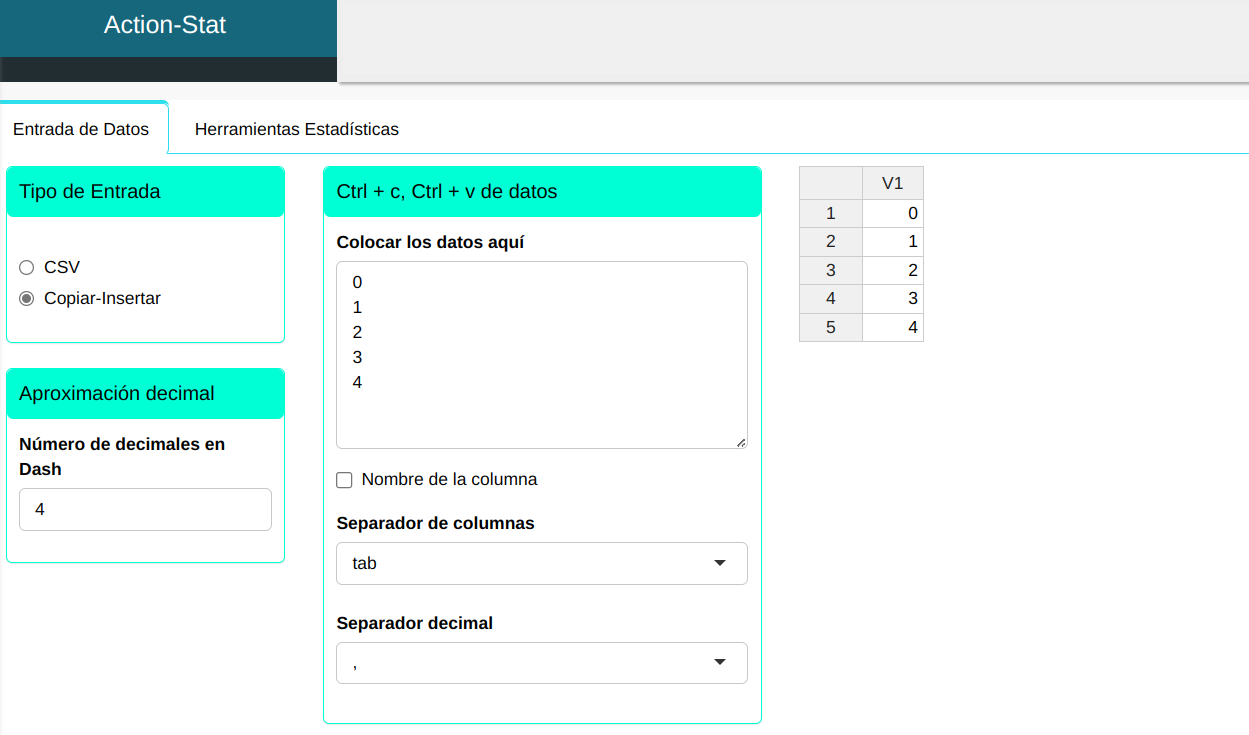
Para calcular la densidad de probabilidad, se realiza la siguiente configuración como se muestra en la siguiente figura.
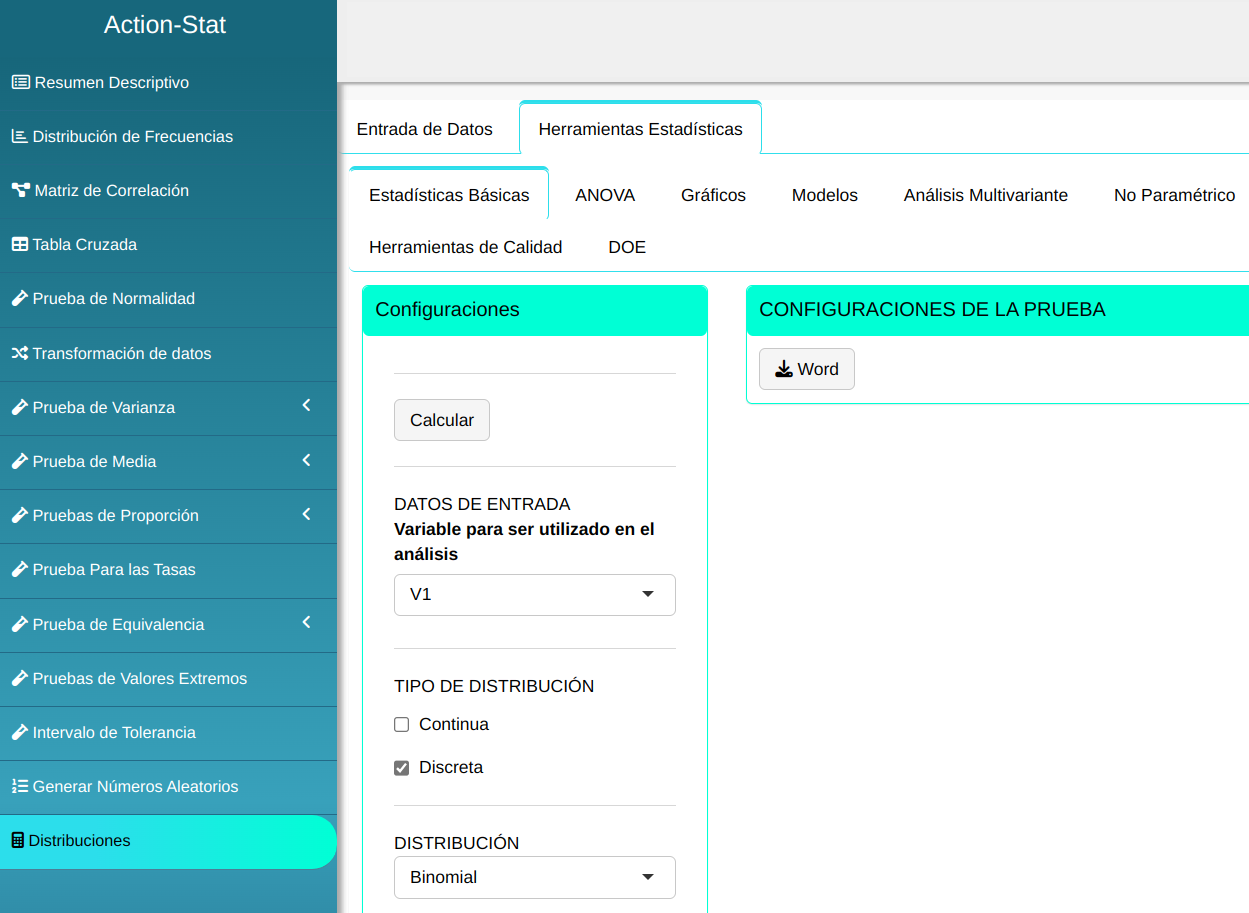
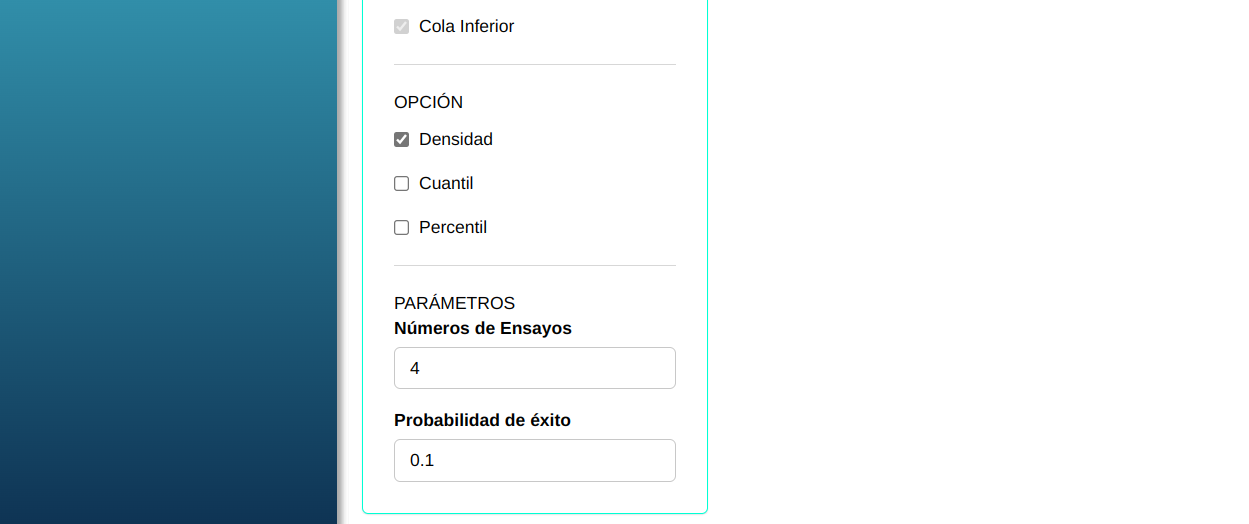
En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:
| Resultados |
|---|
| 0.6561 |
| 0.2916 |
| 0.0486 |
| 0.0036 |
| 0.0001 |
De la tabla vemos que las probabilidades de obtener una pieza defectuosa es 29.16%, sin piezas defectuosas es 65.61%, y obtener dos piezas defectuosas es del 4.86% y para más de dos es inferior al 1%
Ejemplo 5:
Considere una variable aleatoria X con distribución binomial con parámetros n=10 y prob=0.1. Calcular el cuantil de X siendo menor que 0.8 (80%), 0.9 (90%), 0.95 (95%) y 0.975 (97.5%).
Primero, ingresemos las probabilidades para las cuales queremos descubrir los cuantiles de la distribución de intereses.
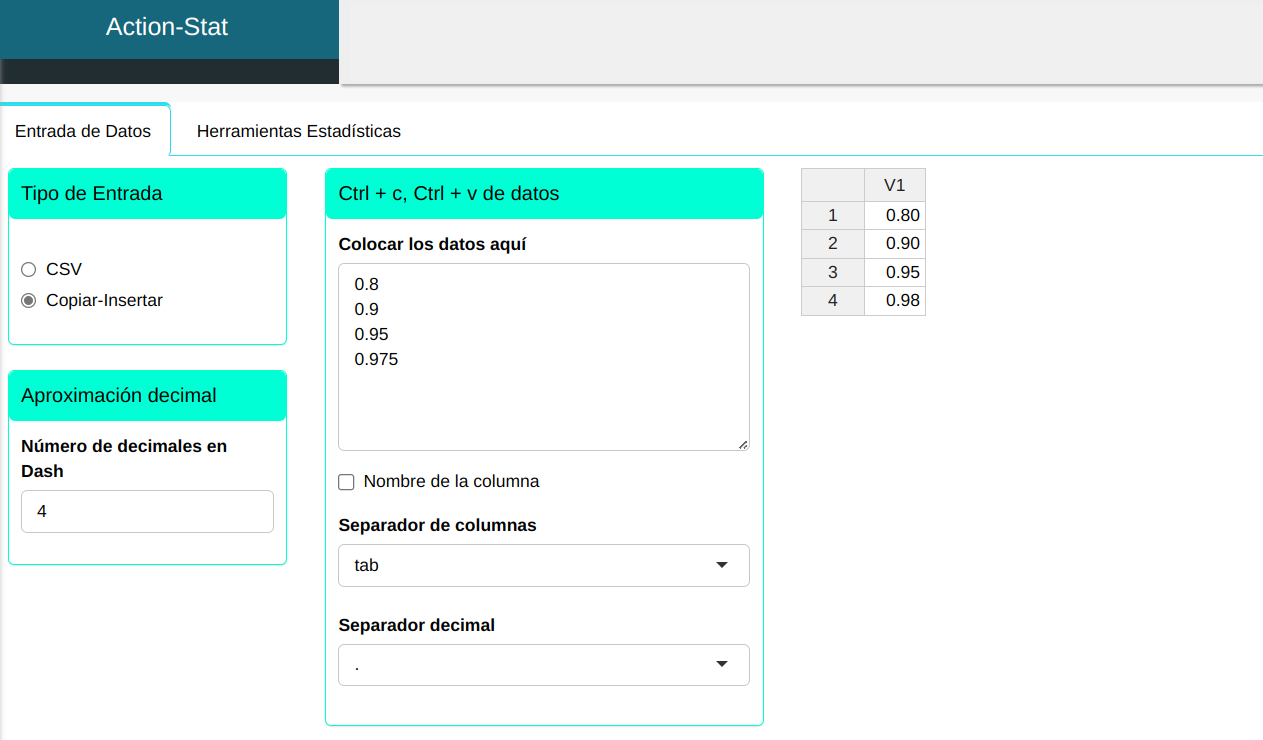
Para calcular los cuantiles, se realiza la siguiente configuración como se muestra en la siguiente figura.
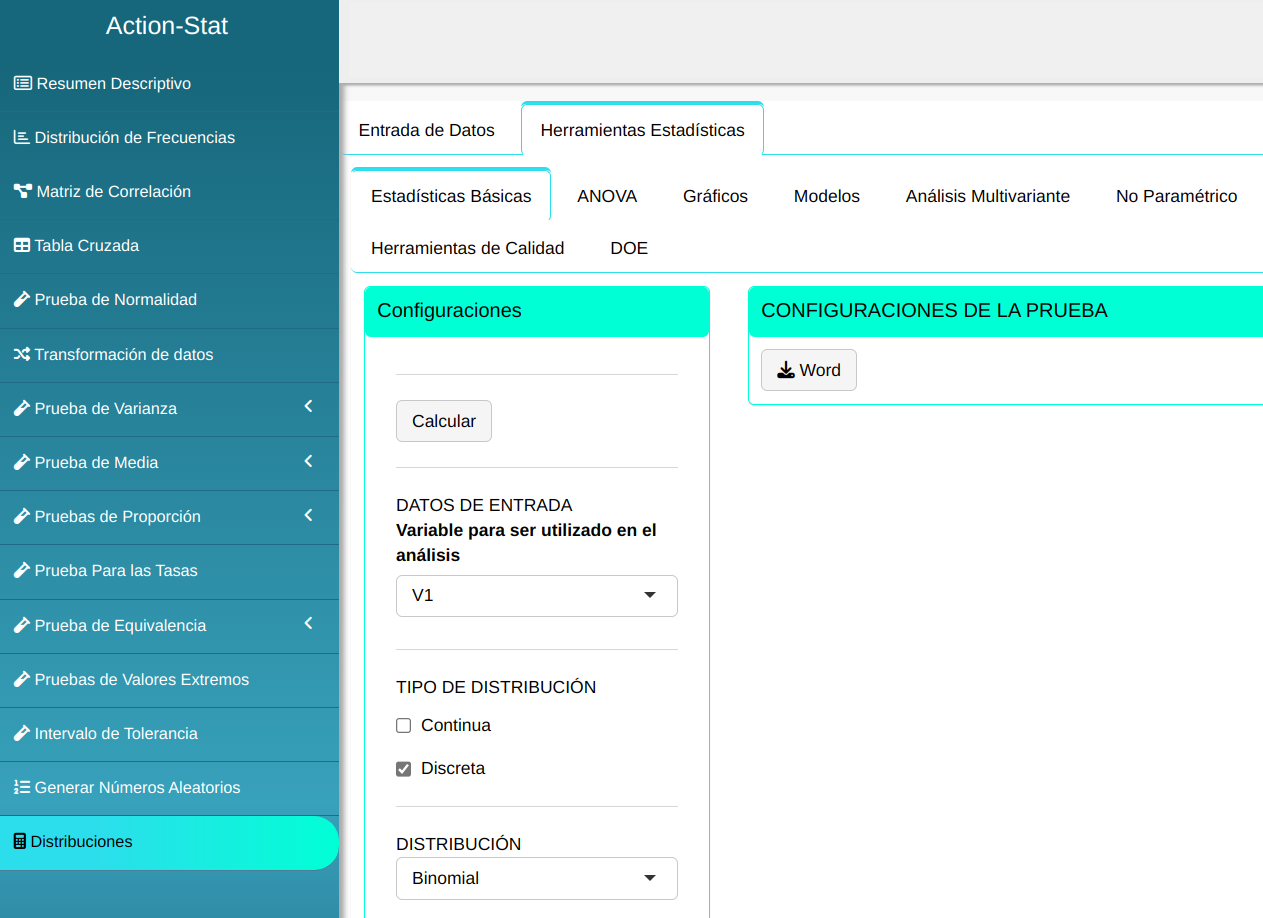
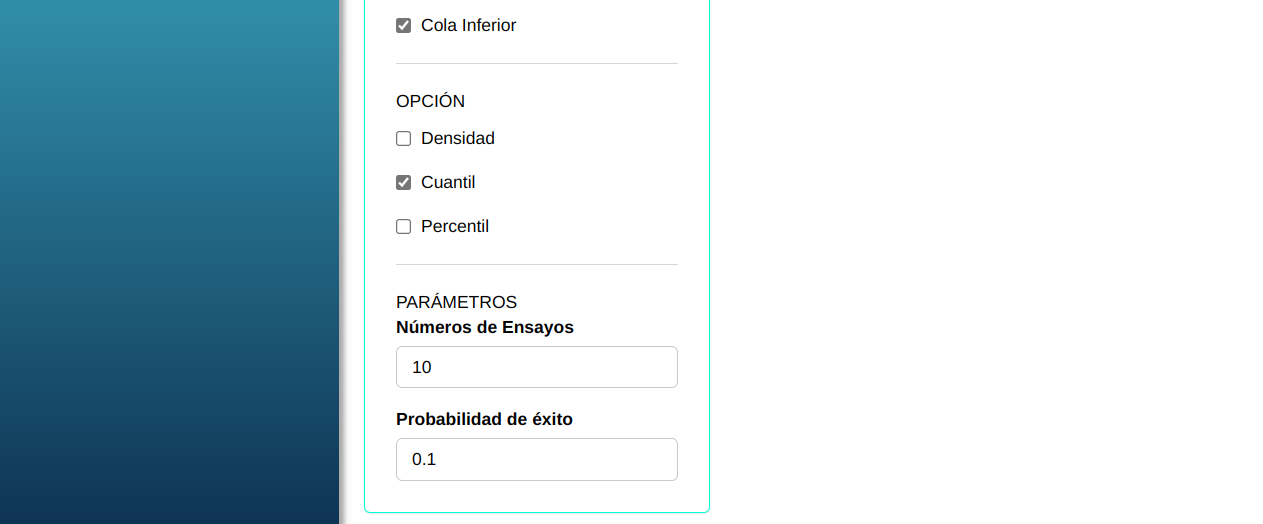
En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:
| Resultados |
|---|
| 2 |
| 2 |
| 3 |
| 3 |
Si el proceso es un experimento de 10 ensayos con un 10% de probabilidad de éxito
- En el 80% de los casos observamos como máximo 2 éxitos.
- En el 90% de los casos observamos como máximo 2 éxitos.
- En el 95% de los casos observamos como máximo 3 éxitos.
- En el 97.5% de los casos observamos como máximo 3 éxitos.
Ejemplo 6:
Supongamos que en una línea de producción la probabilidad de obtener una pieza defectuosa (éxito) es p=0.1. Se toma una muestra de 10 piezas para su inspección. ¿Cuál es la probabilidad de obtener 3 piezas defectuosas o menos?
Primero, ingresemos el valor con el que calcularemos el percentil.
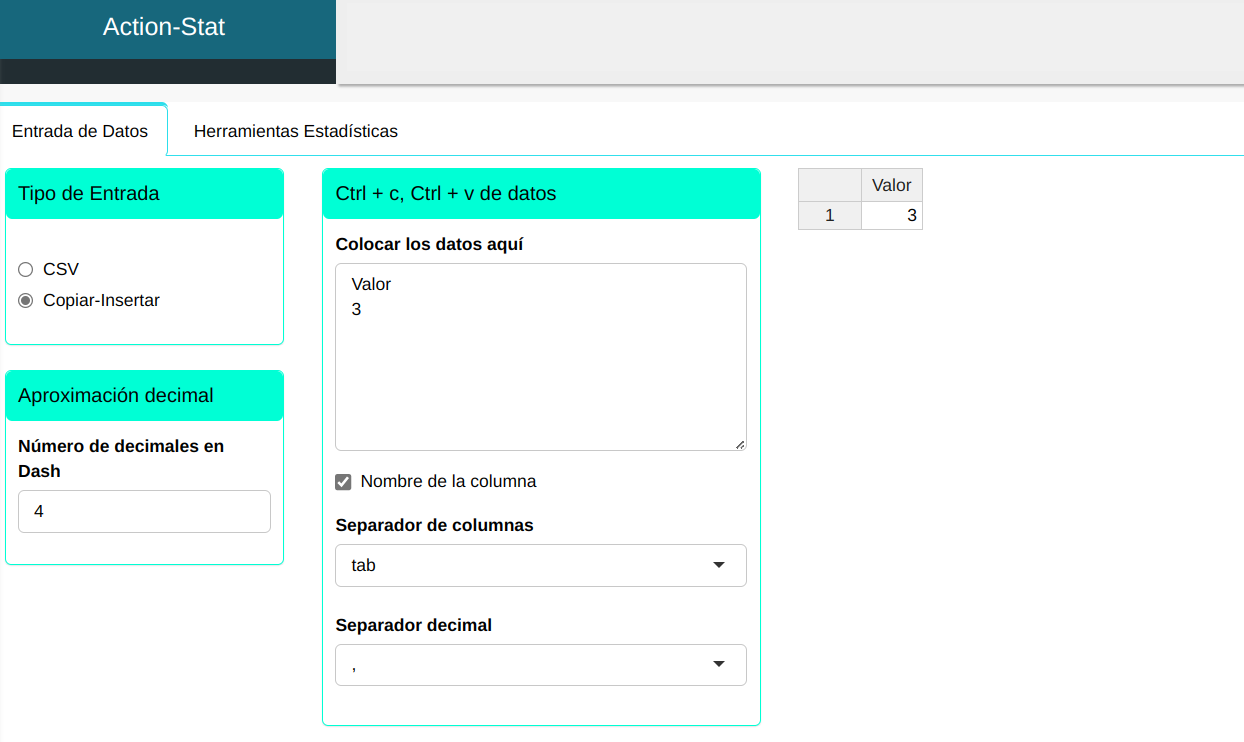
Para calcular los percentiles, se realiza la siguiente configuración como se muestra en la siguiente figura.
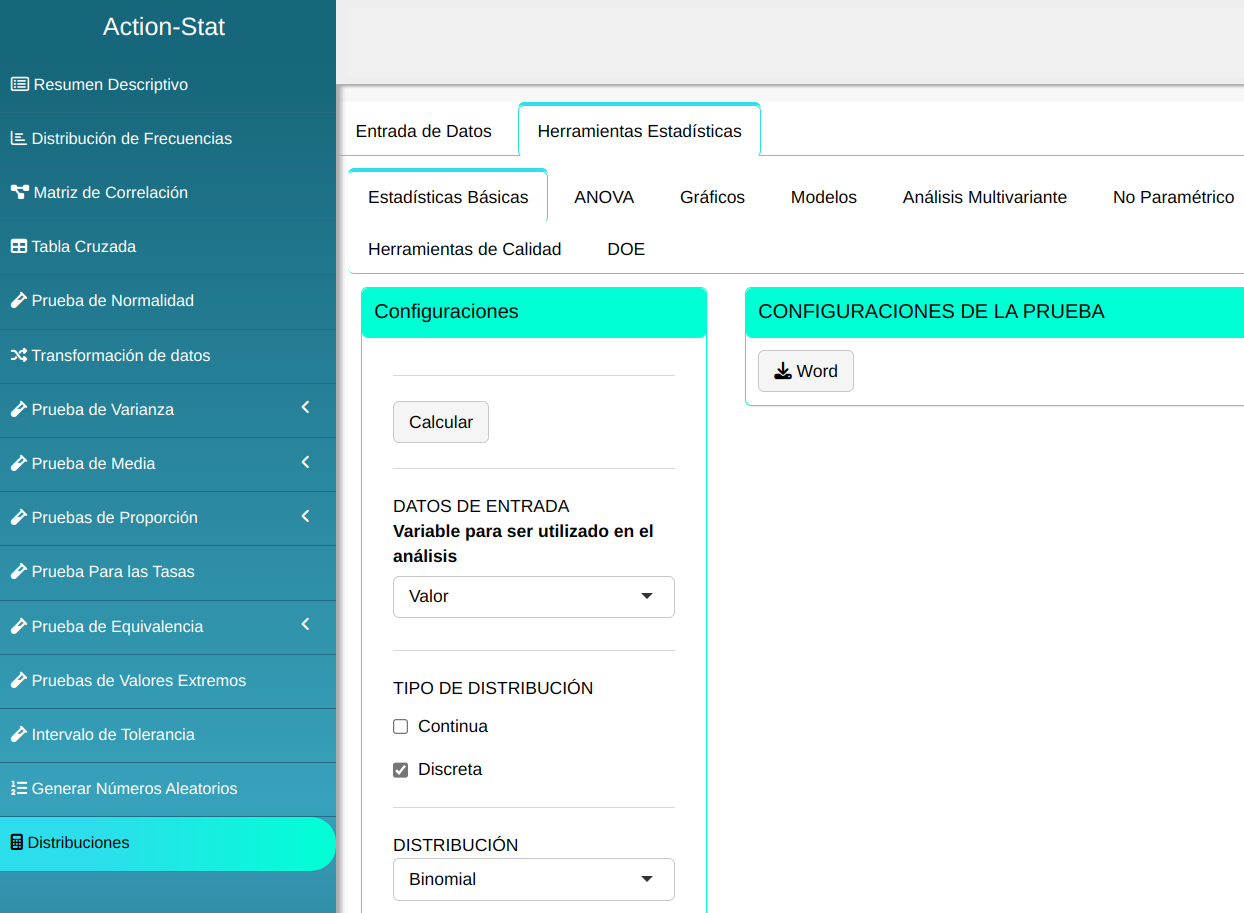
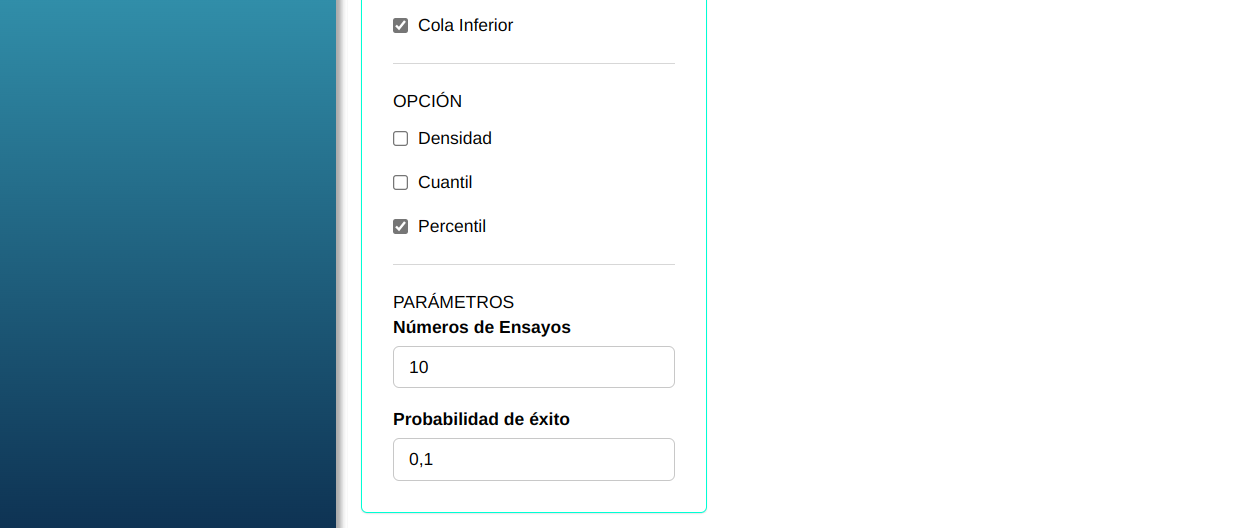
En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:
| vetNum |
|---|
| 0.9872048 |
Según la cantidad liberada la probabilidad de obtener 3 piezas defectuosas o menos es aproximadamente del 98.72%.