13. Intervalo de tolerancia

El intervalo de tolerancia define los límites superiores y/o inferiores dentro de los cuales un determinado porcentaje característico/específico se encuentra dentro de un nivel de confianza declarado.

Ejemplo:

Se desea determinar un porcentaje del 90% de la población con un nivel de confianza del 95%.

Altura
1.68
1.81
1.89
1.78
1.73
1.79
1.90
1.86
1.76
1.72
1.78
1.84
1.81
1.67
1.86
1.74
1.95
1.88
1.92
1.81
1.70
1.81
1.70
1.81
1.74
1.89
1.91
1.80
1.82
1.76
1.71
1.86
1.66
1.85
1.83
1.7

---

Subiremos los datos al sistema.

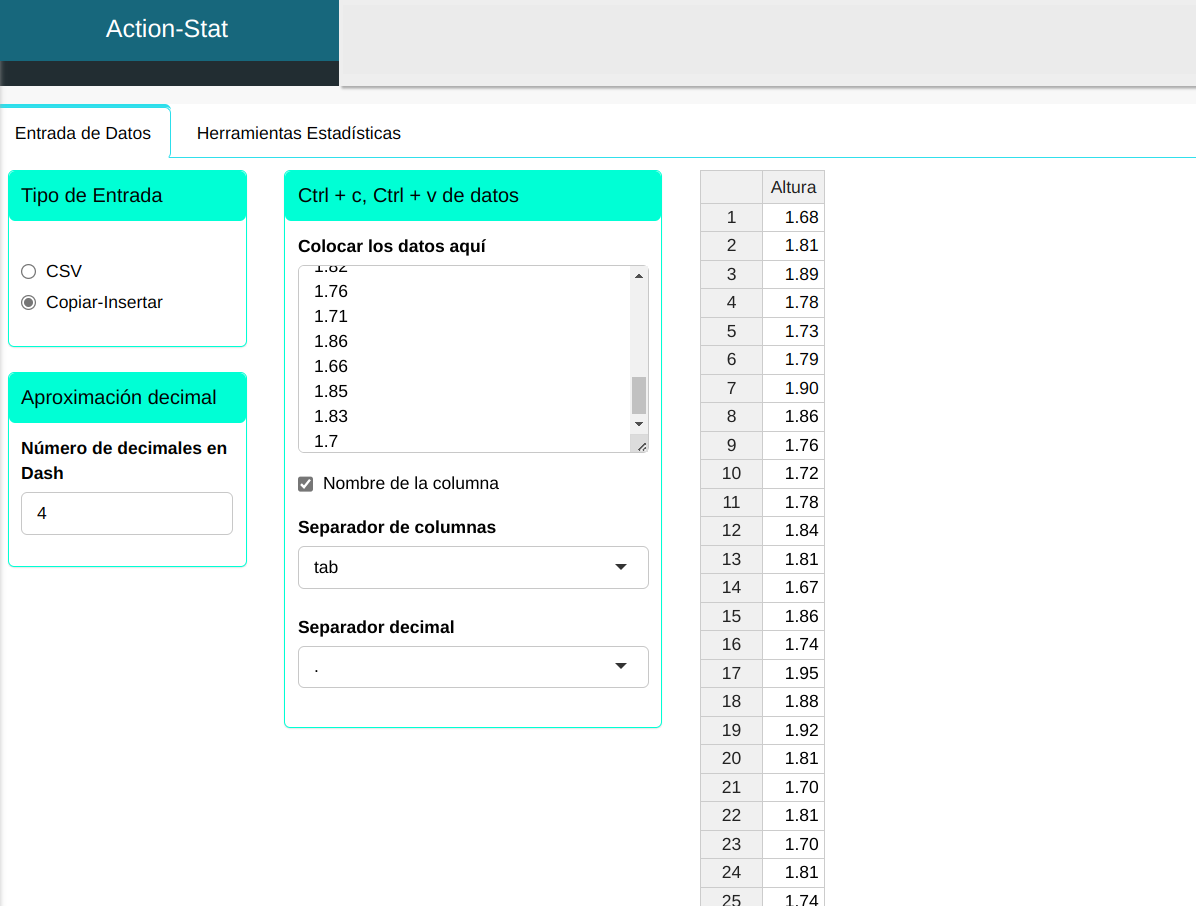
Para calcular el intervalo de tolerancia, se realiza la siguiente configuración que se muestra en la figura siguiente.

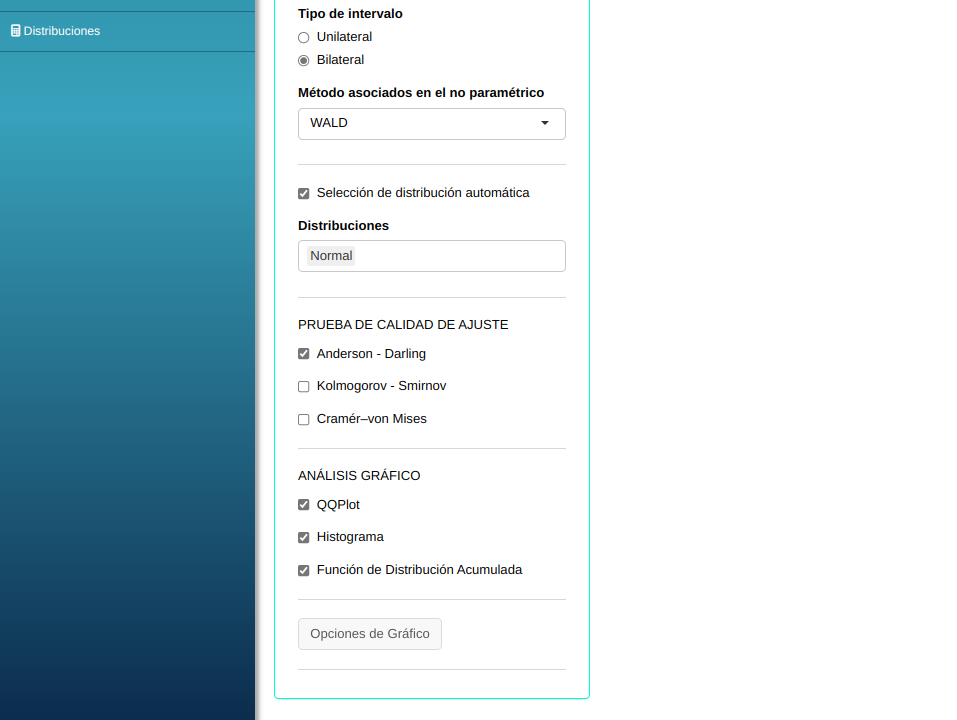
Clicando en Calcular obtenemos los resultados. También se puede generar y descargar los resultados en un archivo Word.

Los resultados son:

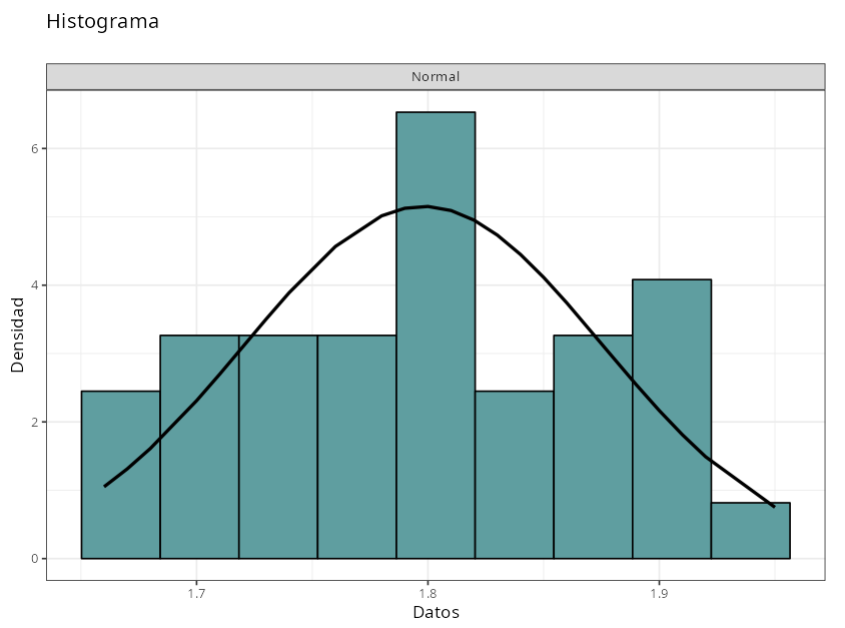
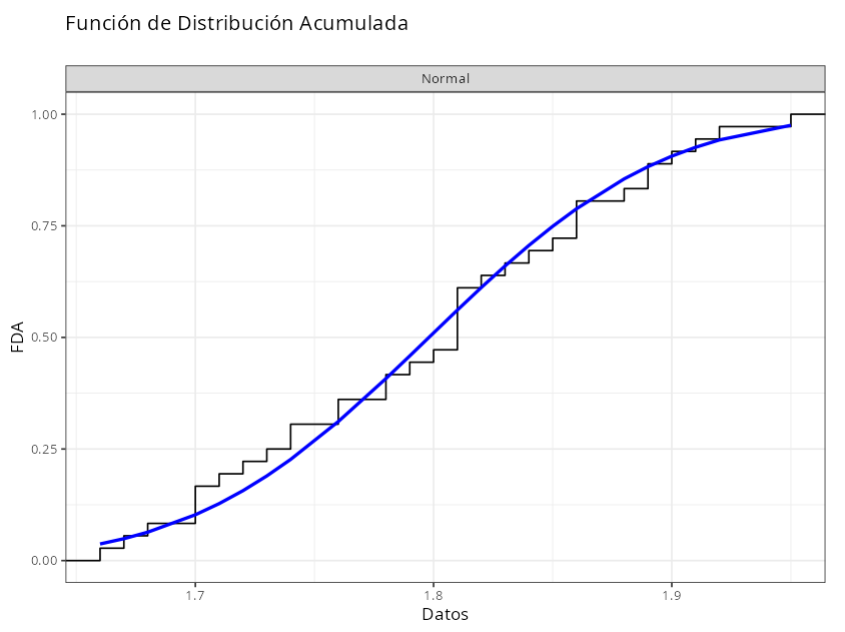
	Distribución Ajustada
	$\quad \qquad$Normal

---

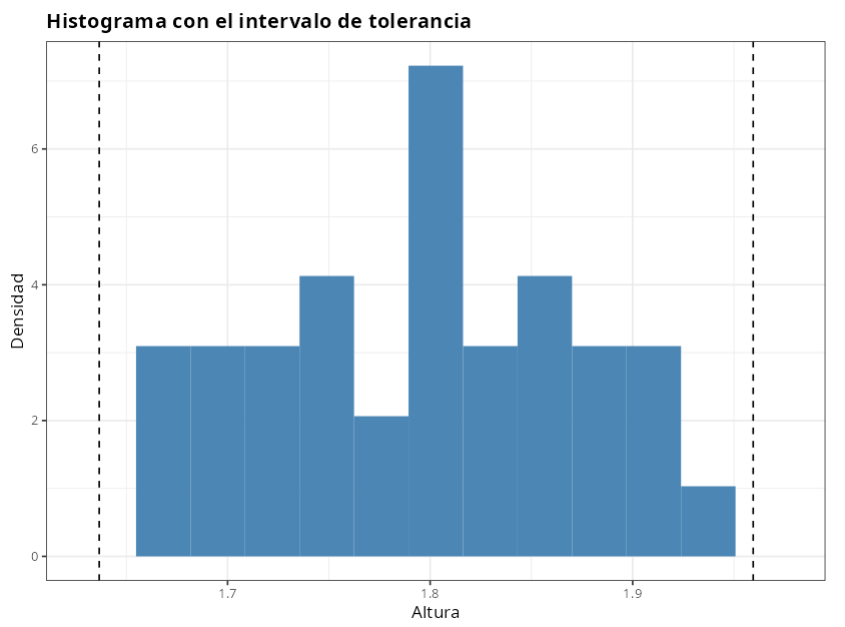
Intervalo de tolerancia

Nivel de significancia	Proporción de población	Límite inferior	Límite superior
0.05	0.900	1.637	1.959

---

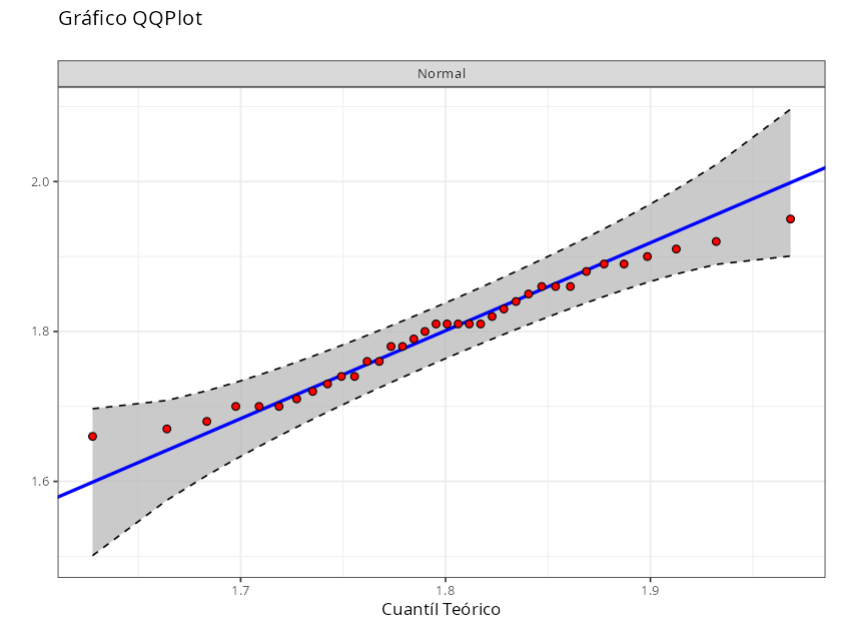
Anderson-Darling

Distribuciones	Estadísticas	P-valor
Normal ($\mu = 1.8, \quad \sigma = 0.077$)	0.291	0.589

---