1. Resumen descriptivo
Etapa inicial de un análisis, utilizada para describir, organizar y resumir, los aspectos importantes de los datos recopilados.
Detalles
El resumen descriptivo nos permite obtener diversa información sobre el conjunto de datos: mínimo, máximo, suma, suma cuadrática, tamaño de la muestra, 1.er cuartil, 3.er cuartil y tri-media. Además de esta información, es posible calcular las medidas de posición (media y mediana), medidas de dispersión (desviación estándar de la media, desviación estándar, varianza y amplitud) y otras estadísticas descriptivas como asimetría y curtosis.
Ejemplo 1:
Se ha tomado la medida de longitud de 15 rollos de acero y se hará una carga en el sistema:
| 71.16 |
| 71.62 |
| 62.86 |
| 65.30 |
| 65.58 |
| 67.95 |
| 65.72 |
| 63.25 |
| 70.93 |
| 68.78 |
| 78.76 |
| 72.42 |
| 74.09 |
| 66.79 |
| 72.78 |
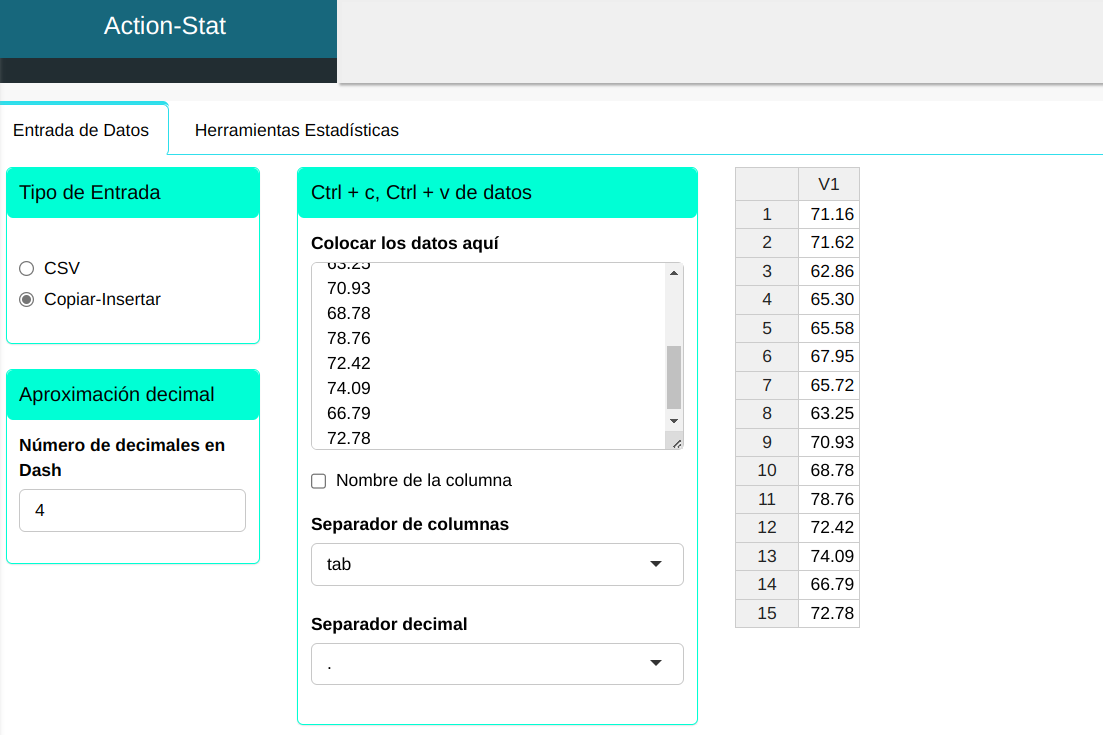
El resumen descriptivo es elaborado conforme la configuración que se muestra en la figura de abajo.
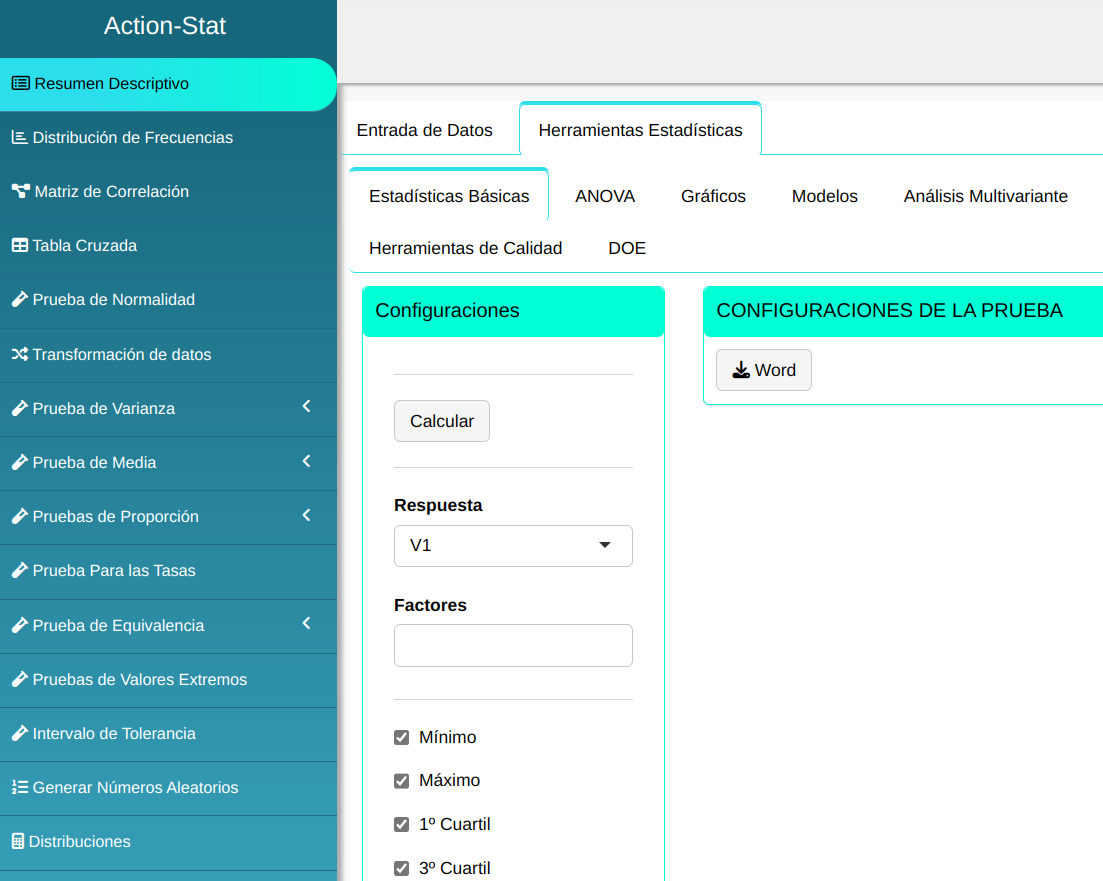
Haga un clic en calcular para visualizar los resultados y descargarlos en un documento de Word.

Obtenemos los siguientes resultados:
| Estadísticas | Descriptivas |
|---|---|
| Mínimo: | 62.86 |
| 1er cuartil: | 65.58 |
| Promedio: | 69.199333 |
| Mediana: | 68.78 |
| Tripromedio: | 68.951538 |
| 3er cuartil: | 72.42 |
| Máximo: | 78.76 |
| Suma: | 1.037.99 |
| Suma cuadrática: | 72102.9673 |
| Desviación estándar de la media: | 1.1438267 |
| Desviación estándar: | 4.430022 |
| Variación: | 19.625092 |
| Coeficiente de variación: | 6.401827 |
| Asimetría: | 0.358057 |
| Curtosis: | -0.799861 |
| Amplitud: | 15.900 |
| Tamaño de la muestra: | 15 |
-
La media y la mediana son representativas de la distribución global de la longitud de los rollos de alambre en la muestra.
-
La variabilidad resultante es considerable si las longitudes de los rollos del cable debe estar próximos. Esto se puede ver a través de la dispersión.
-
La función de distribución es más achatada que la distribución normal porque la curtosis es menor que cero. Ahora, como el valor de asimetría es positivo, pero pequeño, la función de distribución tiene una cola un poco más larga en el lado derecho, es decir, la distribución es asimétrica hacia la derecha.
-
Tanto la media como la mediana pueden considerarse representantes de la distribución general de los datos muestrales porque ambos tienen valores próximos. Sin embargo, cuando el valor de la mediana es muy diferente de la media, es recomendable considerar siempre la mediana como el valor de referencia más importante.
Ejemplo 2:
La medición del diámetro de las piezas fue realizada por cuatro operadores, A, B, C y D, en las mismas condiciones. Se eligieron 6 piezas al azar y las medidas obtenidas se encuentran en la siguiente tabla. En este caso tenemos un conjunto de datos con un único factor, Operadores, y con cuatro niveles, Operador A, Operador B, Operador C y Operador D.
| Niveles | Datos |
|---|---|
| A | 1.688109 |
| A | 1.685566 |
| A | 1.672408 |
| A | 1.680943 |
| A | 1.679250 |
| A | 1.682141 |
| B | 1.663774 |
| B | 1.665943 |
| B | 1.669364 |
| B | 1.671857 |
| B | 1.665928 |
| B | 1.670507 |
| C | 1.658883 |
| C | 1.660408 |
| C | 1.663021 |
| C | 1.662004 |
| C | 1.661382 |
| C | 1.655508 |
| D | 1.672502 |
| D | 1.670928 |
| D | 1.683285 |
| D | 1.686528 |
| D | 1.677429 |
| D | 1.681030 |
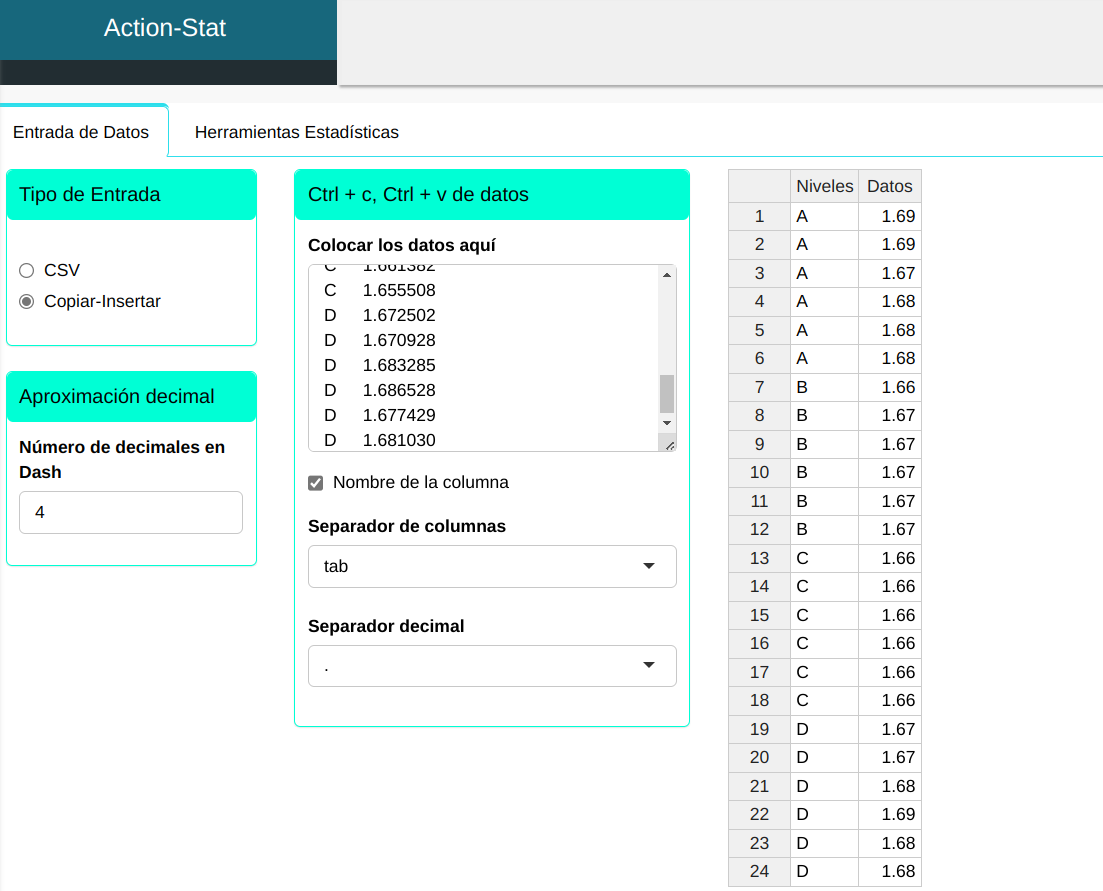
El resumen descriptivo es elaborado conforme la configuración que se muestra en la figura de abajo.
Haga un clic en calcular para visualizar los resultados y descargarlos en un documento de Word.

Obtenemos los siguientes resultados:
| Niveles | A | B | C | D |
|---|---|---|---|---|
| Mínimo | 1.672408 | 1.663774 | 1.655508 | 1.670928 |
| 1.er cuartil | 1.6775395 | 1.6653895 | 1.65803925 | 1.67221085 |
| Media | 1.6814028 | 1.6678955 | 1.660201 | 1.678617 |
| Mediana | 1.681542 | 1.6676535 | 1,660895 | 1.6792295 |
| Tri-media | 1.6814028 | 1.6678955 | 1.660201 | 1.678617 |
| 3.er cuartil | 1.68620175 | 1.6708445 | 1.6622583 | 1.6840958 |
| Máximo | 1.688109 | 1.671857 | 1.663021 | 1.686528 |
| Suma | 10.088109 | 10.007373 | 9.961206 | 10.071702 |
| Suma cuadrática | 16.96284153 | 16.69130173 | 16.53764056 | 16.90671831 |
| Desviación estándar de la media | 0.002225628 | 0.0012824453 | 0.00110154 | 0.00250414 |
| Desviación estándar | 0.00545165 | 0.0031413367 | 0.00269823 | 0.006133873 |
| Variación | 0.00007972 | 0.00000987 | 0.00000728 | 0.00003762 |
| Coeficiente de variación | 0.32423250 | 0.188341338 | 0.16252422 | 0.36541231 |
| Asimetría | -0.3740836 | -0.010343887 | -0.64230944 | -0.05347545 |
| Curtosis | -1.3224643 | -1.94651104 | -1.22707584 | -1.90258576 |
| Amplitud | 0.015701 | 0.008083 | 0.007513 | 0.0156 |
| Tamaño de la muestra | 6 | 6 | 6 | 6 |
Las medias y medianas para cada nivel son representantes de la distribución global del diámetro de piezas medido por cada uno de los operadores.
-
La variabilidad resultante no es significativa.
-
La función de distribución es más achatada que la distribución normal porque la curtosis es negativa a todos los niveles. Ahora, como el valor de la asimetría también es negativa en todos los niveles, la función de distribución tiene una cola un poco más larga en el lado izquierdo, es decir, la distribución es asimétrica a la izquierda.