11. Prueba de Equivalencia
La herramienta Prueba de equivalencia ofrece análisis para datos continuos con varianzas iguales o diferentes, y también ofrece pruebas de no inferioridad, superioridad y equivalencia para datos binarios.
Ejemplo 1:
En este ejemplo, se desea probar si una nueva metodología es superior a la metodología compendiada. Para ello, se evalúa la proporción de resultados positivos de ambos métodos. Los datos resumidos figuran en el cuadro siguiente.
| Resultados | Alternativo | Compendial |
|---|---|---|
| Positivo | 133 | 105 |
| Estéril | 17 | 45 |
| Total | 150 | 150 |
Se Realizara la prueba en el sistema. Configurando conforme la figura de abajo
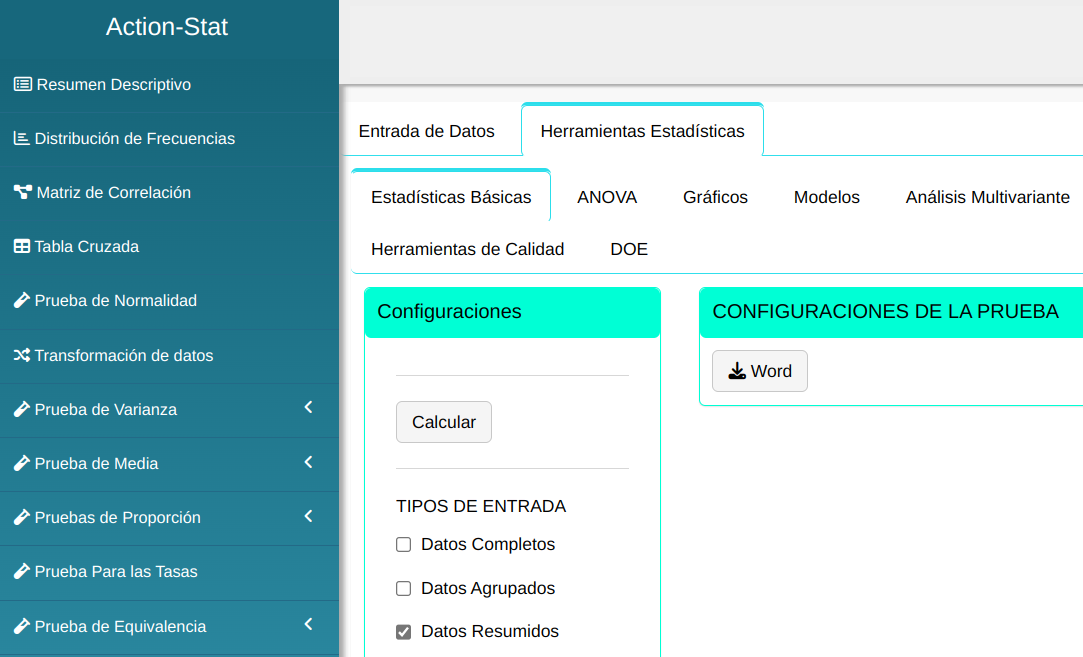
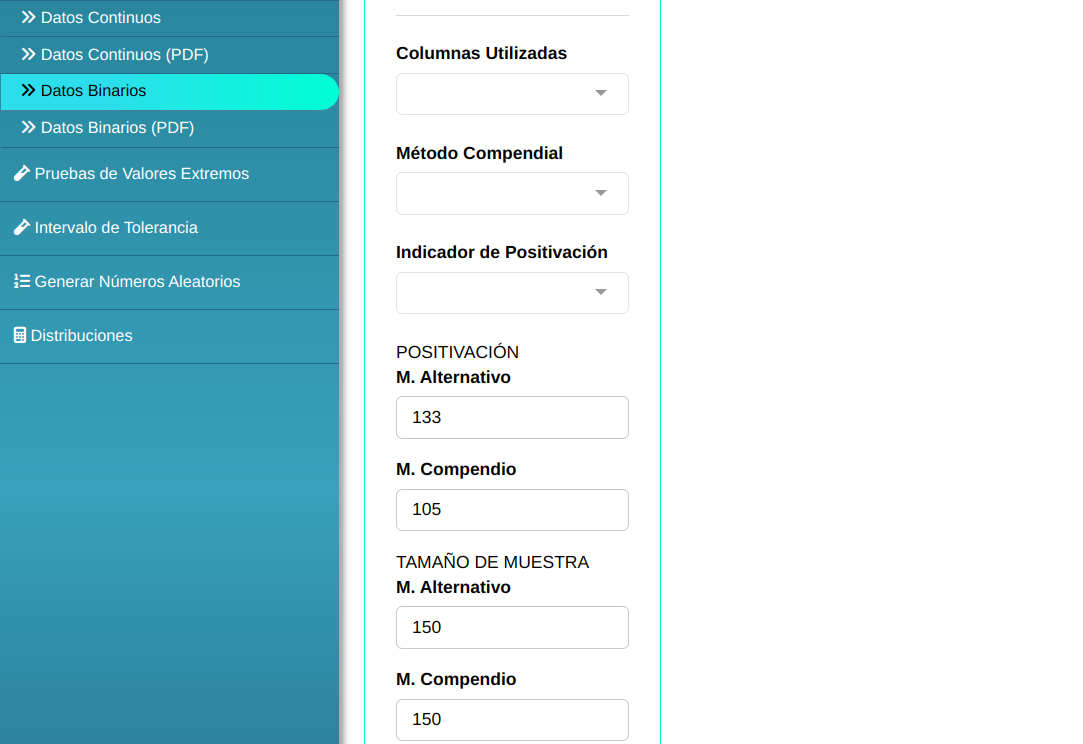
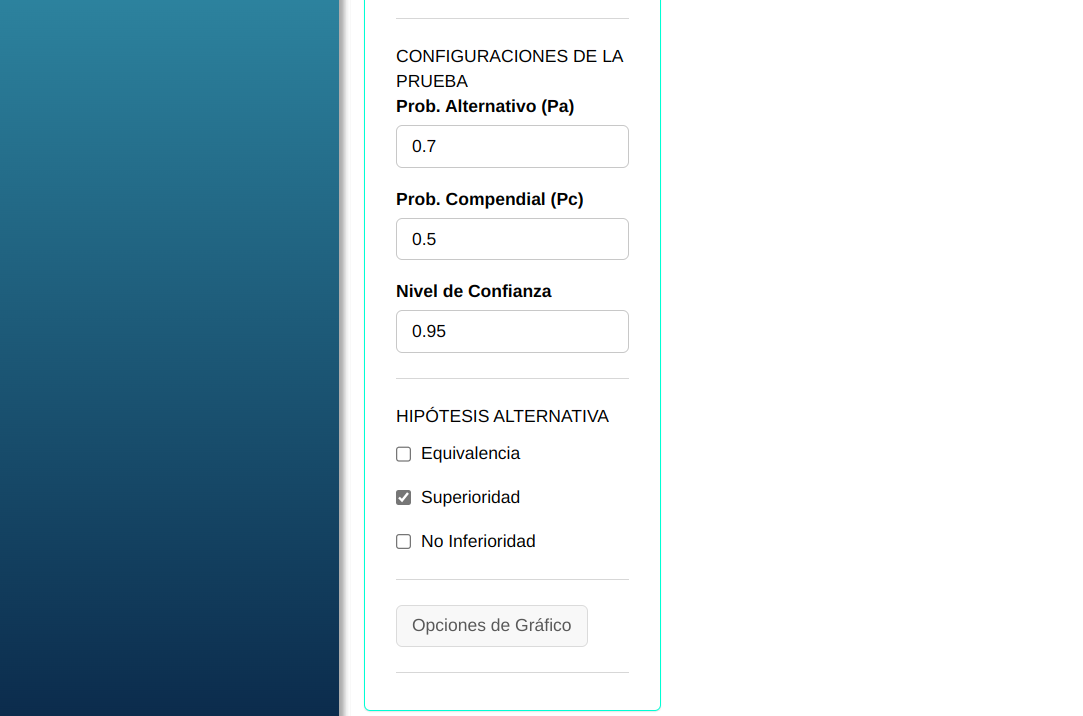
En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:
Esta sección se basa en la norma de la United States Pharmacopeia [1], que define la hipótesis de Superioridad como la proporción de resultados positivos para el procedimiento alternativo (PA) menos la proporción de resultados positivos para el procedimiento tradicional o compendio (PC), tiene un margen de tolerancia de Superioridad (Delta = 0,2). La hipótesis viene dada por
$$H_0: Pa-Pc \leq \Delta$$
$$H_1: Pa-Pc > \Delta$$
| Símbolo | Leyenda/Fórmula |
|---|---|
| Na | Tamaño de Muestra del Método Alternativo |
| Nc | Tamaño de Muestra del Método Compendial |
| Xa | Cantidad de resultados positivos del método alternativo |
| Xc | Cantidad de resultados positivos del método tradicional |
| Pa | Proporción para el método alternativo |
| Pc | Proporción para el método Compendial |
| ^Pa | Xa/Na |
| ^Pc | Xc/Nc |
| theta | Nc/Na |
| R | Pa/Pc |
| a | 1+theta |
| b | -[R(1+theta ^Pc)+theta+^Pa] |
| c | R(^Pa+theta ^Pc) |
| ~Pa | (-b-raiz(b²-4ac))/2a |
| ~Pc | ~Pa/R |
| V | [~Pa(1-~Pa)]/Na+R²[~Pc(1-~Pc)]/Nc |
| Z | (^Pa-R^Pc)/raiz(V) |
$\quad$ Resultados de la Prueba de Superioridad
Resultados del Método Compendial
| Cantidad | Proporción Estimada | |
|---|---|---|
| Positivo | 105 | 0.7 |
| Estéril | 45 | 0.3 |
| Total | 150 | 1.0 |
Resultados del Método Alternativo
| Cantidad | Proporción Estimada | |
|---|---|---|
| Positivo | 133 | 0.8866667 |
| Estéril | 17 | 0.1133333 |
| Total | 150 | 1.0000000 |
Parámetros de la prueba
$$H_0: Pa-Pc \leq \Delta$$
$$H_1: Pa-Pc > \Delta$$
| Valor | |
|---|---|
| Theta | 1.000000000 |
| Razón de Proporciones (R) | 1.400000000 |
| a | 2.000000000 |
| b | -4.266666667 |
| c | 2.221333333 |
| ~pa | 0.902012146 |
| ~pc | 0.644294390 |
| Varianza (V) | 0.003583849 |
| Raiz(V) | 0.059865256 |
| ^pa-R*^pc | -0.093333333 |
| Estadística Z | -1.559056788 |
Criterio de Rechazo
| Valor | |
|---|---|
| Nivel de significância | 0.0500000 |
| Cuantil de la Normal Estándar - Superioridad | 1.6448536 |
| P-valor | 0.9405085 |
Intervalo de confianza
| Valor | |
|---|---|
| Nivel de Confianza | 0.95 |
| Límite Superior | 0.261502 |
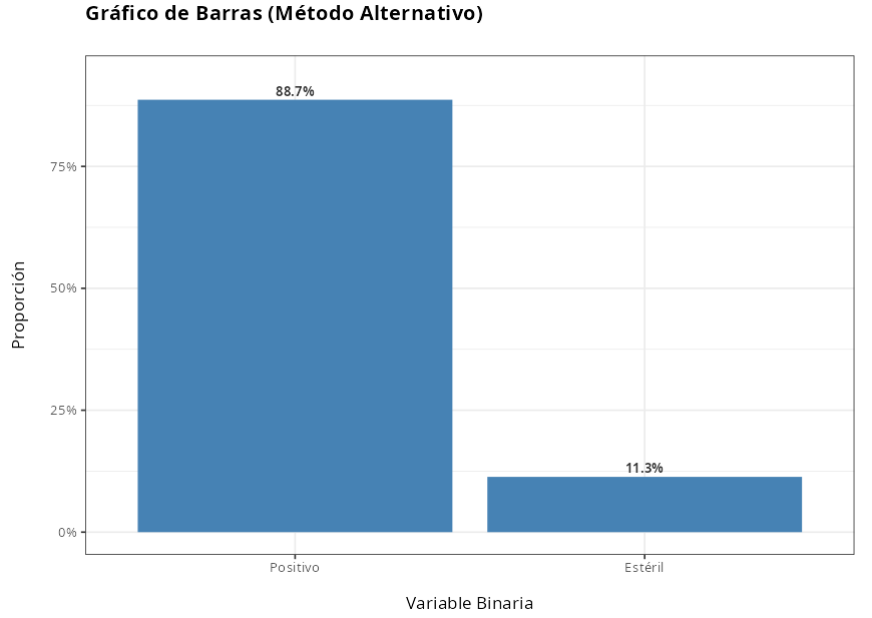
A partir de los resultados obtenidos, no rechazamos la hipótesis nula al nivel de significación del 5%. Por lo tanto, concluimos que el método Alternativo no es superior al método Tradicional.
Ejemplo 2:
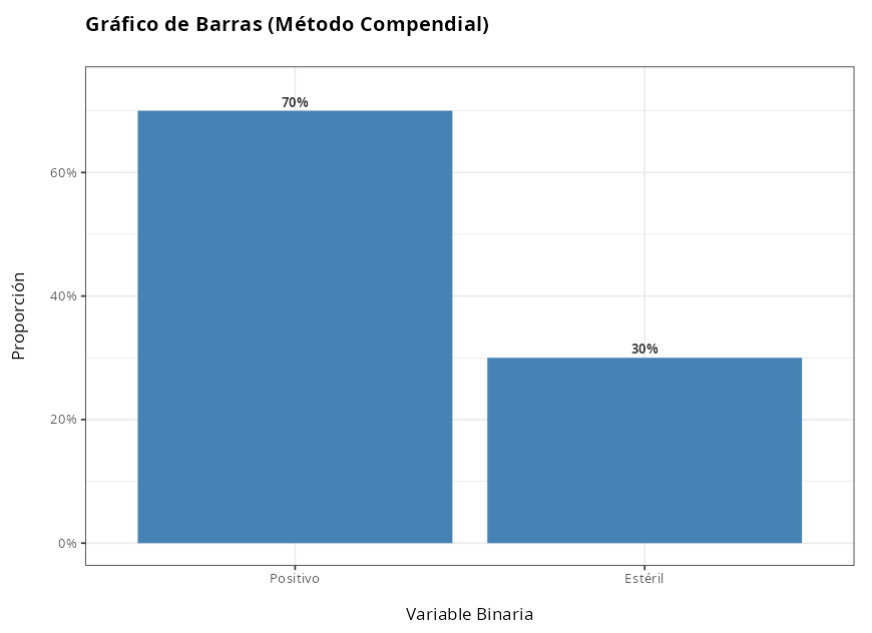
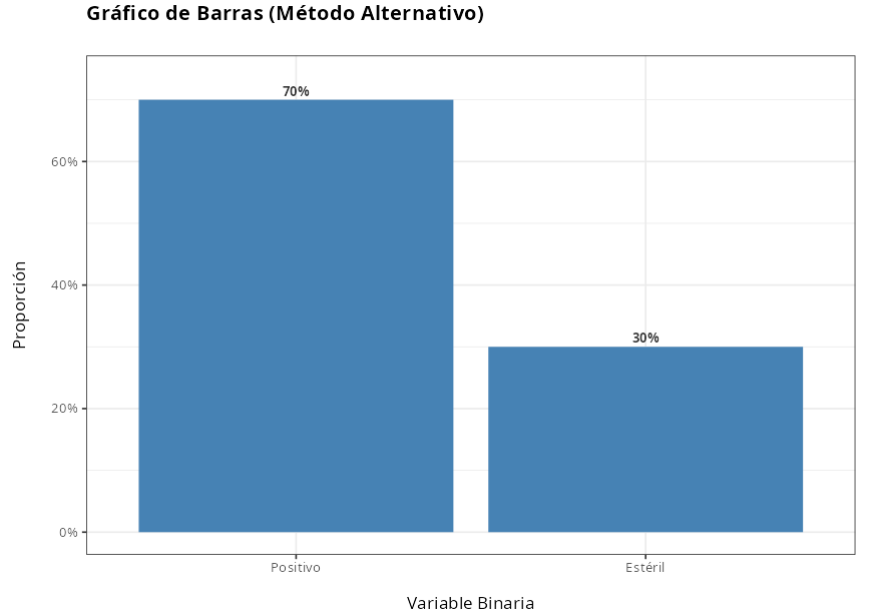
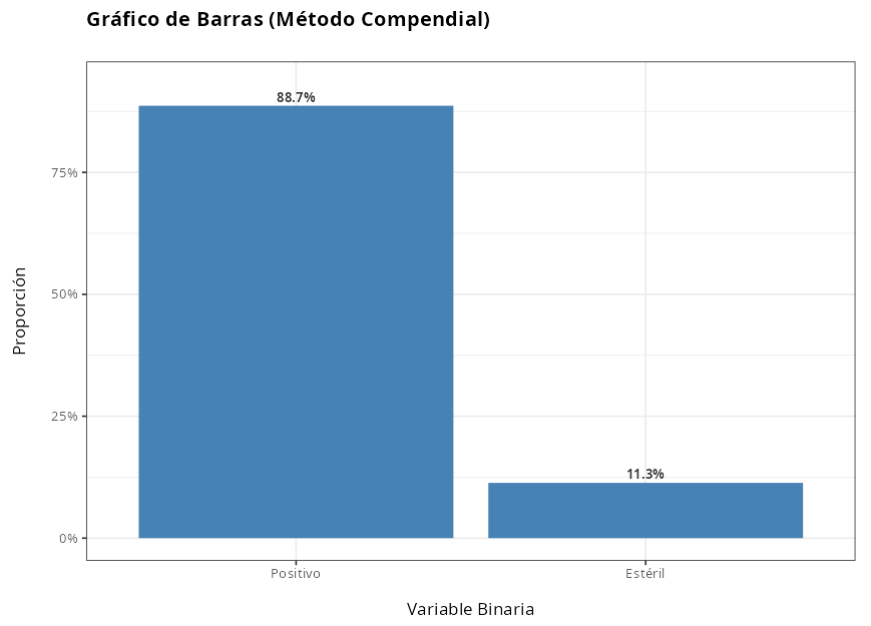
En este ejemplo se desea probar si una nueva metodología es equivalente a la metodología compendial. Para ello se evalúa la proporción de resultados positivos de ambos métodos. Los datos resumidos se dan en la tabla. próximo
| Resultados | Alternativo | Compendial |
|---|---|---|
| Positivo | 105 | 133 |
| Estéril | 45 | 17 |
| Total | 150 | 150 |
En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:
Esta sección se basa en la norma de la United States Pharmacopeia [1], que define la hipótesis de Equivalencia como la proporción de resultados positivos para el procedimiento alternativo (PA) menos la proporción de resultados positivos para el procedimiento tradicional o compendial (PC), tiene un margen de tolerancia de Equivalencia (Delta = -0,2). La hipótesis de equivalencia viene dada por:
$$H_0: Pa-Pc \leq -\Delta \quad \textrm{ó} \quad Pa-Pc \geq \Delta$$
$$H_1: -\Delta < Pa-Pc < \Delta$$
| Símbolo | Leyenda/Fórmula |
|---|---|
| Na | Tamaño de Muestra del Método Alternativo |
| Nc | Tamaño de Muestra del Método Compendial |
| Xa | Cantidad de resultados positivos del método alternativo |
| Xc | Cantidad de resultados positivos del método tradicional |
| Pa | Proporción para el método alternativo |
| Pc | Proporción para el método Compendial |
| ^Pa | Xa/Na |
| ^Pc | Xc/Nc |
| theta? | Nc/Na |
| R | Pa/Pc |
| a | 1+theta |
| b | -[R(1+theta ^Pc)+theta+^Pa] |
| c | R(^Pa+theta^Pc) |
| ~Pa | (-b-raiz(b²-4ac))/2a |
| ~Pc | ~Pa/R |
| V | [~Pa(1-~Pa)]/Na+R²[~Pc(1-~Pc)]/Nc |
| Z | (~Pa - R~Pa)/raiz(V) |
$\quad$ Resultados de la Prueba de Equivalencia
Resultados del Método Compendial
| Cantidad | Proporción Estimada | |
|---|---|---|
| Positivo | 133 | 0.8866667 |
| Estéril | 17 | 0.1133333 |
| Total | 150 | 1.0000000 |
Resultados del Método Alternativo
| Cantidad | Proporción Estimada | |
|---|---|---|
| Positivo | 105 | 0.7 |
| Estéril | 45 | 0.3 |
| Total | 150 | 1.0 |
Parámetros de la prueba
$$H_{01}: Pa-Pc \leq -\Delta$$
$$H_{11}: Pa-Pc > -\Delta$$
| Valor | |
|---|---|
| Theta | 1.000000000 |
| Razón de Proporciones (R) | 0.714285714 |
| a | 2.000000000 |
| b | -3.047619048 |
| c | 1.133333333 |
| ~pa | 0.644294390 |
| ~pc | 0.902012146 |
| Varianza (V) | 0.001828494 |
| Raiz(V) | 0.042760897 |
| ^pa-R*^pc | 0.066666667 |
| Estadística Z | 1.559056788 |
Parámetros de la Prueba
$$H_{01}: Pa-Pc \geq \Delta$$
$$H_{11}: Pa-Pc < \Delta$$
| Valor | |
|---|---|
| Theta | 1.000000000 |
| Razón de Proporciones (R) | 1.400000000 |
| a | 2.000000000 |
| b | -4.341333333 |
| c | 2.221333333 |
| ~pa | 0.825946021 |
| ~pc | 0.589961444 |
| Varianza (V) | 0.004119312 |
| Raiz(V) | 0.064181866 |
| ^pa-R*^pc | -0.541333333 |
| Estadística Z | -8.434365747 |
Criterio de rechazo
| Valor | |
|---|---|
| Nivel de significância | 0.05000000 |
| Cuantil de la Normal Estándar - No inferioridad | 1.64485363 |
| Cuantil de la Normal Estándar - Superioridad | -1.64485363 |
| P-valor | 0.05949147 |
Intervalo de Confianza
| Valor | |
|---|---|
| Nivel de Confianza | 0.95 |
| Límite Inferior | -0.26150165 |
| Límite Superior | -0.11183168 |
A partir de los resultados obtenidos, no rechazamos la hipótesis nula al nivel de significación del 5%. Por lo tanto, concluimos que el método Alternativo no es equivalente al método Tradicional.
Ejemplo 3:
En este ejemplo, se desea probar si una nueva metodología no es inferior a la metodología compendial. Para ello, se evalúa la proporción de resultados positivos de ambos métodos. Los datos resumidos figuran en el cuadro siguiente.
| Resultados | Alternativo | Compendial |
|---|---|---|
| Positivo | 105 | 133 |
| Estéril | 45 | 17 |
| Total | 150 | 150 |
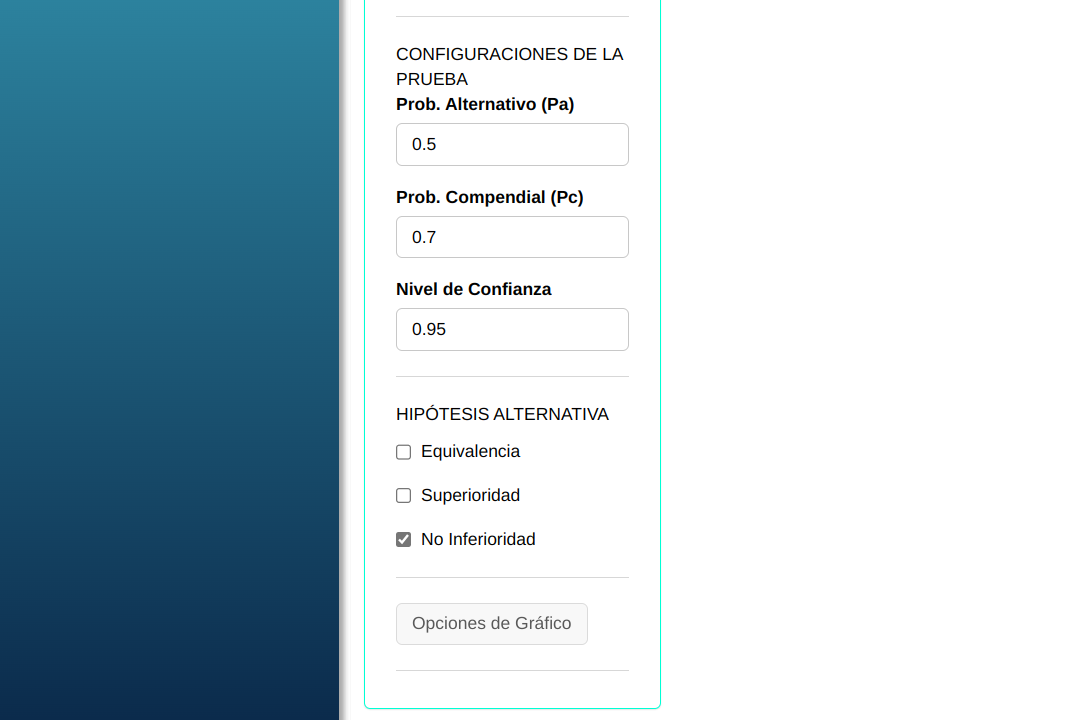
En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:
Esta sección se basa en la norma de la United States Pharmacopeia [1], que define la hipótesis de no inferioridad como la proporción de resultados positivos para el procedimiento alternativo (PA) menos la proporción de resultados positivos para el procedimiento tradicional o procedimiento compendiado (PC), tiene un margen de tolerancia de no inferioridad ($\Delta = -0,2$). La hipótesis de no inferioridad viene dada por:
$$H_0: Pa-Pc \leq -\Delta$$ y $$H_1: Pa-Pc > -\Delta$$
| Símbolo | Leyenda/Fórmula |
|---|---|
| Na | Tamaño de Muestra del Método Alternativo |
| Nc | Tamaño de Muestra del Método Compendial |
| Xa | Cantidad de resultados positivos del método alternativo |
| Xc | Cantidad de resultados positivos del método tradicional |
| Pa | Proporción para el método alternativo |
| Pc | Proporción para el método Compendial |
| ^Pa | Xa/Na |
| ^Pc | Xc/Nc |
| theta? | Nc/Na |
| R | Pa/Pc |
| a | 1+theta |
| b | -[R(1+theta ^Pc)+theta+^Pa] |
| c | R(^Pa+theta ^Pc) |
| ~Pa | (-b-raiz(b²-4ac))/2a |
| ~Pc | ~Pa/R |
| V | [~Pa(1-~Pa)]/Na+R²[~Pc(1-~Pc)]/Nc |
| Z | (~Pa-R~Pa)/raiz(V) |
$\quad$ Resultados de la Prueba de No Inferioridad
Resultado del Método Compendial
| Cantidad | Proporción Estimada | |
|---|---|---|
| Positivo | 133 | 0.8866667 |
| Estéril | 17 | 0.1133333 |
| Total | 150 | 1.0000000 |
Resultado del Método Alternativo
| Cantidad | Proporción Estimada | |
|---|---|---|
| Positivo | 105 | 0.7 |
| Estéril | 45 | 0.3 |
| Total | 150 | 1.0 |
Parâmetros de teste
$$H_0: Pa-Pc \leq -\Delta$$
$$H_1: Pa-Pc > -\Delta$$
| Valor | |
|---|---|
| Theta | 1.000000000 |
| Razon de Proporciones (R) | 0.714285714 |
| a | 2.000000000 |
| b | -3.047619048 |
| c | 1.133333333 |
| ~pa | 0.644294390 |
| ~pc | 0.902012146 |
| Varianza (V) | 0.001828494 |
| Raiz(V) | 0.042760897 |
| ^pa-R*^pc | 0.066666667 |
| Estadística Z | 1.559056788 |
Criterio de rechazo
| Valor | |
|---|---|
| Nivel de significancia | 0.05000000 |
| Cuantil de la Normal Estándar - No inferioridad | 1.64485363 |
| P-Valor | 0.05949147 |
Intervalo de Confianza
| Valor | |
|---|---|
| Nivel de Confianza | 0.95 |
| Límite Inferior | -0.26150165 |
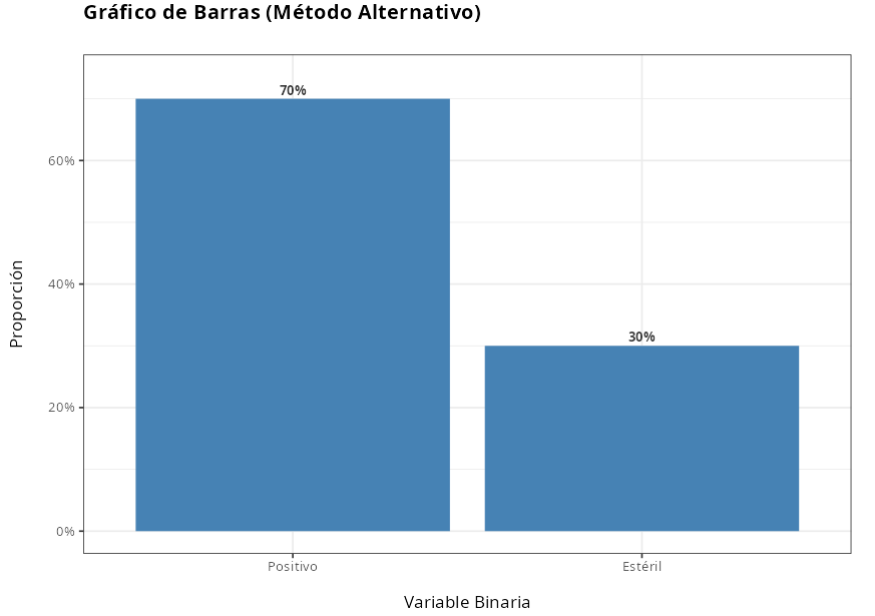
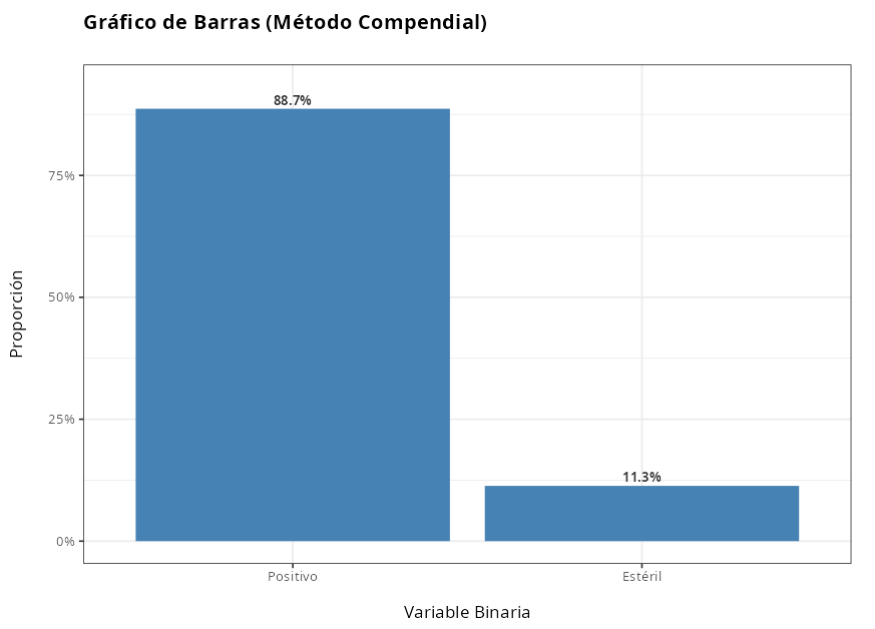
A partir de los resultados obtenidos, no rechazamos la hipótesis nula al nivel de significación del 5%. Por lo tanto, concluimos que el método alternativo es inferior al método tradicional.
Ejemplo 4:
Haremos la prueba de equivalencia para datos continuos. Se desea comprobar la equivalencia de dos laboratorios en la concentración de un determinado medicamento. Para ello, se recogieron 10 medicamentos de cada laboratorio.
| Datos | Factor |
|---|---|
| 100,5449 | A |
| 99,67155 | A |
| 99,32921 | A |
| 100,0855 | A |
| 100,2163 | A |
| 100,0495 | A |
| 100,0238 | A |
| 99,28651 | A |
| 100,1467 | A |
| 99,72407 | A |
| 102,0206 | C |
| 101,0006 | C |
| 101,8330 | C |
| 101,7111 | C |
| 101,7244 | C |
| 98,65855 | C |
| 100,3181 | C |
| 100,9711 | C |
| 99,16993 | C |
| 100,7830 | C |
Haremos un upload de los datos al sistema.
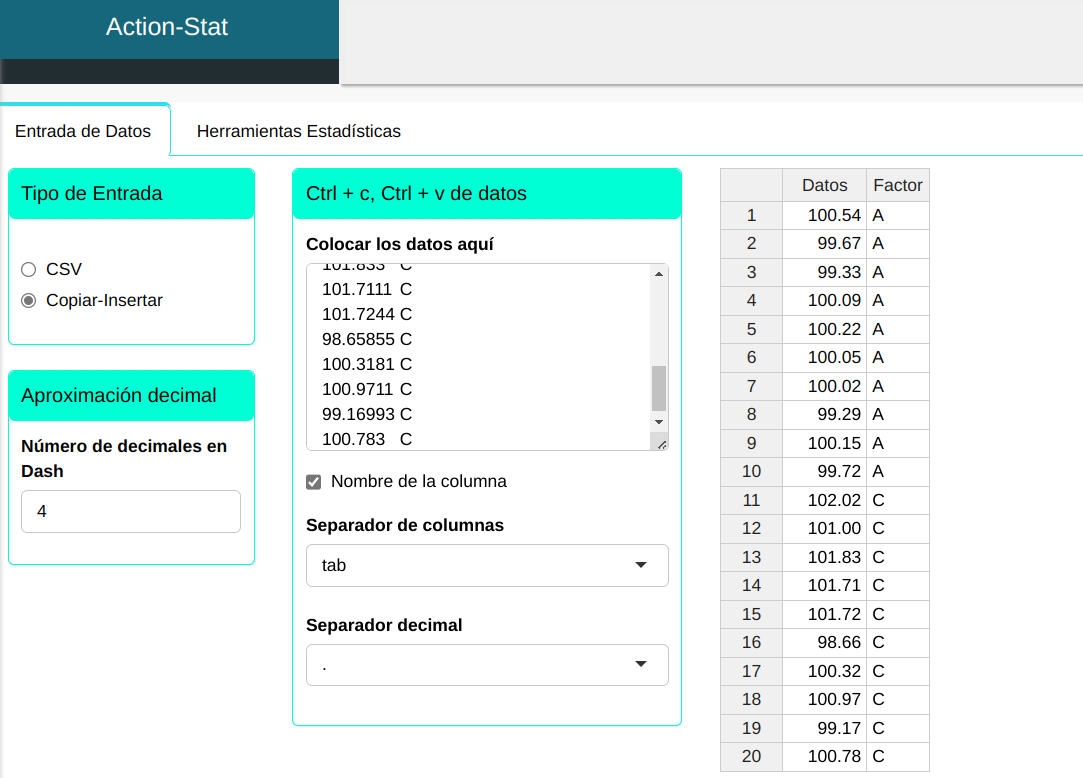
Se realizara la prueba. Configurando conforme a figura de abajo.
En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:
Evaluación de Equivalencia
Para realizar la prueba de equivalencia, realizamos una prueba t con las siguientes hipótesis:
$$H_0: m1-m2 \leq -d \qquad \textrm{ó} \qquad m1-m2 \geq d$$
$$H_1: -d < m1-m2 < d$$
Las cuales pueden ser escritas como:
$$H_{01}: m1-m2 \leq -d \qquad \textrm{y} \qquad H_{11}: m1-m2 \geq -d$$
$$H_{02}: m1-m2 \geq d \qquad \textrm{y} \qquad H_{12}: m1-m2 < d$$
Resultados
| Valores | |
|---|---|
| Grados de Libertad | 11.1581 |
| P-valor | 0.4107 |
| Media - A | 99.9078 |
| Media - C | 100.8190 |
| Desviación Estándar - A | 0.3991 |
| Desviación Estándar - C | 1.1442 |
| Tamaño de la Muestra - A | 10.0000 |
| Tamaño de la Muestra - C | 10.0000 |
| Nivel de Confianza | 0.9500 |
| Límite Inferior | -1.5985 |
| Límite Superior | -0.2239 |
| Margen de equivalencia | 1.0000 |
| Estadística de Test 1 - $H_{01}: m1-m2 \leq -d$ | 0.2316 |
| Estadística de Test 2 - $H_{02}: m1-m2 \geq d$ | 4.9874 |
A un nivel de significación de 0,05, no rechazamos la hipótesis nula, es decir, concluimos que las características probadas no son equivalentes a un nivel de significación del 5%.
A continuación presentamos los resultados de la Prueba de Varianza.
| Muestra | Grupos |
|---|---|
| 100.5449 | A |
| 99.6716 | A |
| 99.3292 | A |
| 100.0855 | A |
| 100.2163 | A |
| 100.0495 | A |
| 100.0238 | A |
| 99.2865 | A |
| 100.1467 | A |
| 99.7241 | A |
| 102.0206 | C |
| 101.0006 | C |
| 101.8330 | C |
| 101.7111 | C |
| 101.7244 | C |
| 98.6586 | C |
| 100.3181 | C |
| 100.9711 | C |
| 99.1699 | C |
| 100.7830 | C |
Prueba para las Varianzas
| Valores | |
|---|---|
| Estadística F | 0.121667 |
| Grados de libertad (Numerador) | 9 |
| Grados de libertad (Denominador) | 9 |
| P-Valor | 0.00436814 |
| Desviación estándar - A | 0.3991091 |
| Desviación estándar - C | 1.144208 |
| Tamaño del A | 10 |
| Tamaño del C | 10 |
| Hipótesis Alternativa Diferente de | 1 |
| Intervalos de Confianza para el cociente de varianzas. | 95,00% |
| Límite Inferior | 0.03022037 |
| Límite Superior | 0.4898308 |
Para un nivel de significación de 0,05 rechazamos la hipótesis nula, es decir, concluimos que las varianzas son estadísticamente diferentes.
A continuación, presentamos el gráfico que contiene el intervalo de confianza y el margen de equivalencia
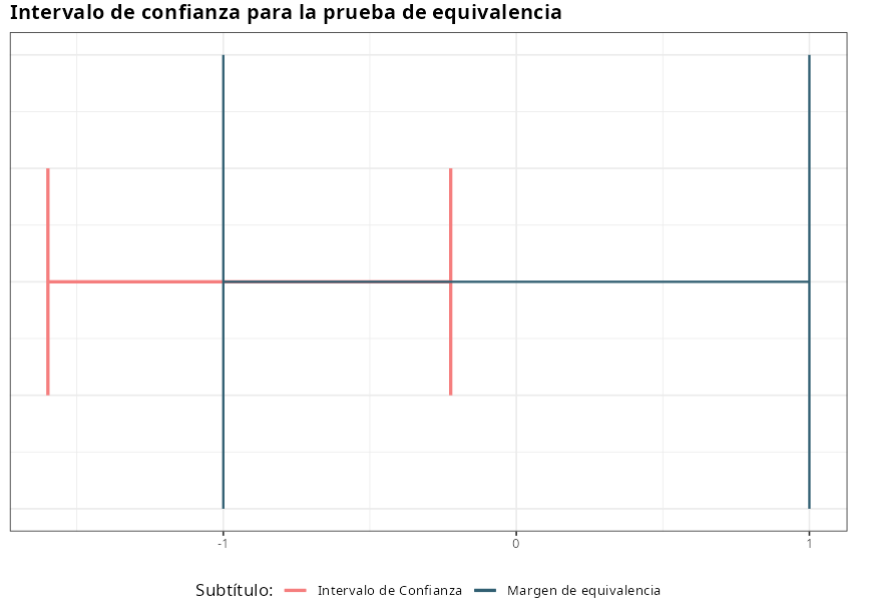
Con un valor P > $\alpha$, no se rechaza la hipótesis nula. Por lo tanto, se concluye que los laboratorios no son equivalentes al nivel de significación $\alpha $= 5%.