5. Prueba de Normalidad
Las pruebas de normalidad se utilizan para determinar si un vector numérico proviene de una distribución normal.
Detalles:
La herramienta de pruebas de normalidad le permite determinar si un conjunto de datos está bien modelado mediante una distribución Normal, utilizando las pruebas de Anderson-Darling, Kolmogorov-Smirnov, Shapiro-Wilk o Ryan-Joiner. Además de las pruebas, la herramienta genera papel de probabilidad, que permite analizar visualmente la normalidad de los datos.
Ejemplo:
Se quiere saber si el peso de determinadas piezas sigue una distribución normal. Para esto se obtuvo una muestra con 11 medidas (peso) de las piezas (en libras).
| 148 |
| 154 |
| 158 |
| 160 |
| 161 |
| 162 |
| 166 |
| 170 |
| 182 |
| 195 |
| 236 |
En seguida se cargará los datos al sistema
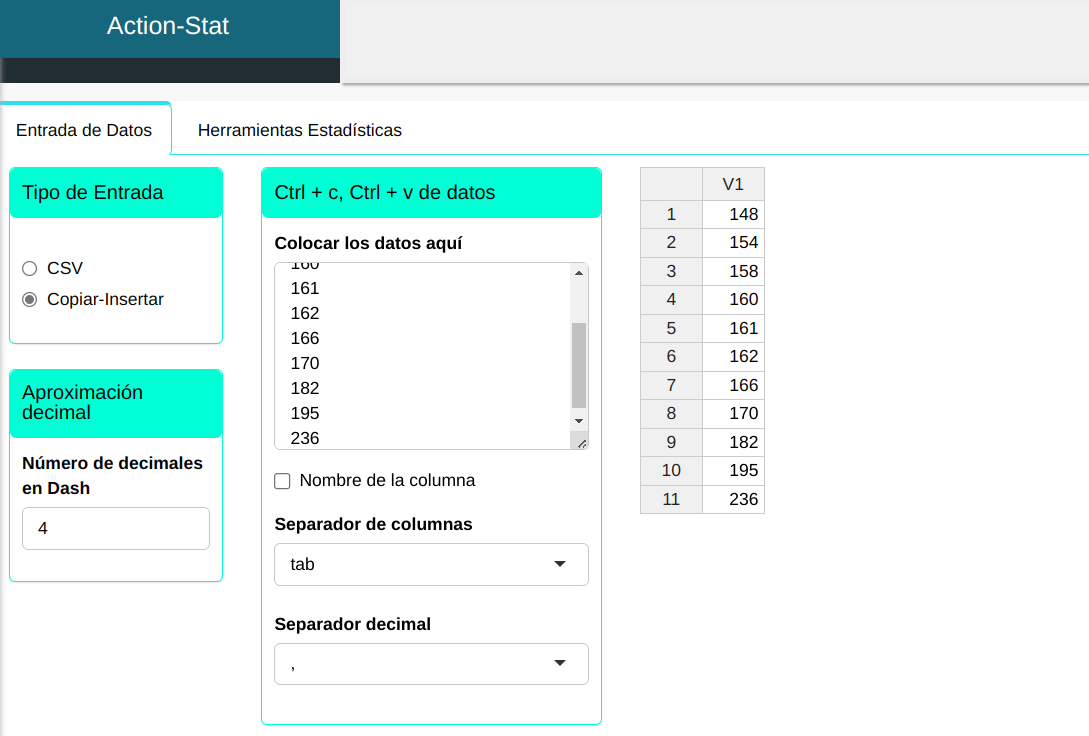
A continuación se realiza la prueba de normalidad.
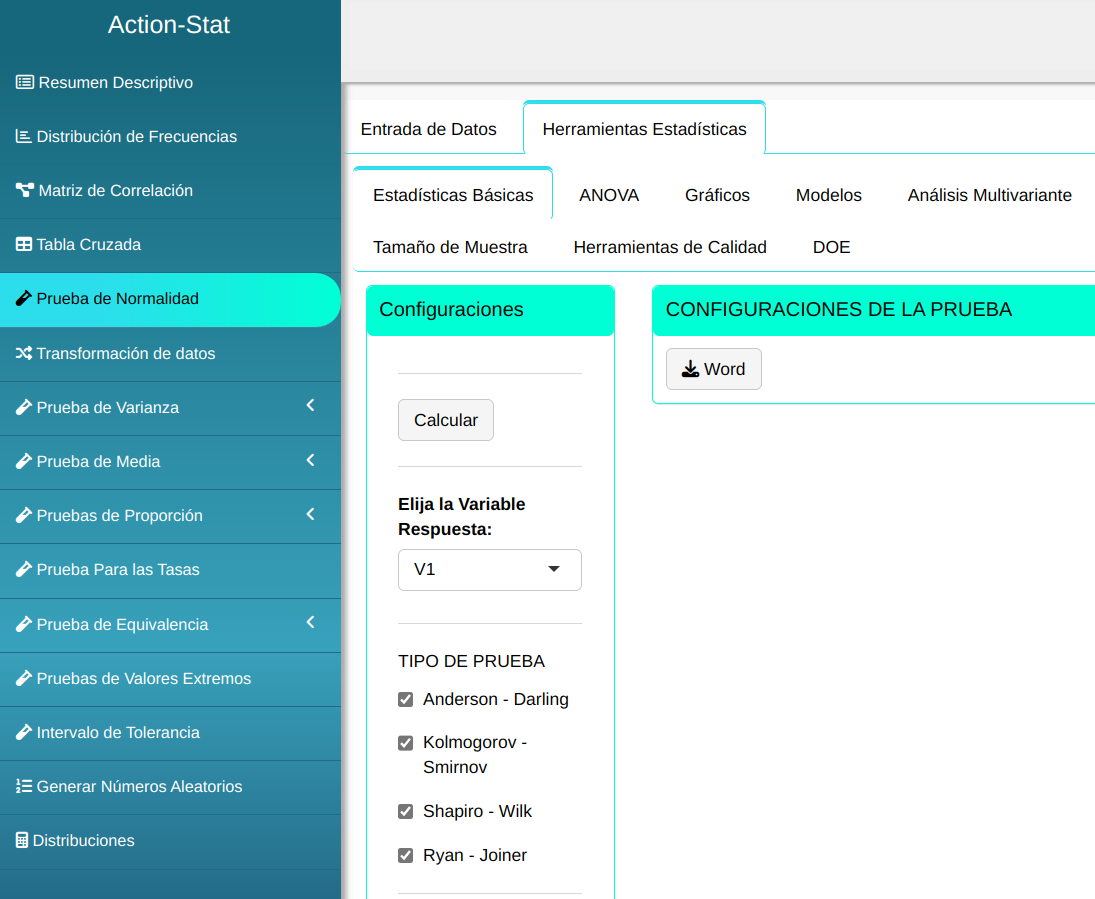
En seguida. haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados obtenidos son.
Pruebas de normalidad
| Estadísticas | P-valor | |
|---|---|---|
| Anderson-Darling | 0.947 | 0.0105 |
| Kolmogorov-Smirnov | 0.259 | 0.0374 |
| Shapiro-Wilk | 0.789 | 0.0067 |
| Ryan-Joiner | 0.878 | 0.0089 |
Outliers (cuantiles)
| Obs. | Cuantiles normales | Datos | Criterio |
|---|---|---|---|
| 10 | 1.10 | 195 | Banda de confianza ( Nivel de confianza=95% ) |
| 11 | 1.69 | 236 | Banda de confianza ( Nivel de confianza=95%) |
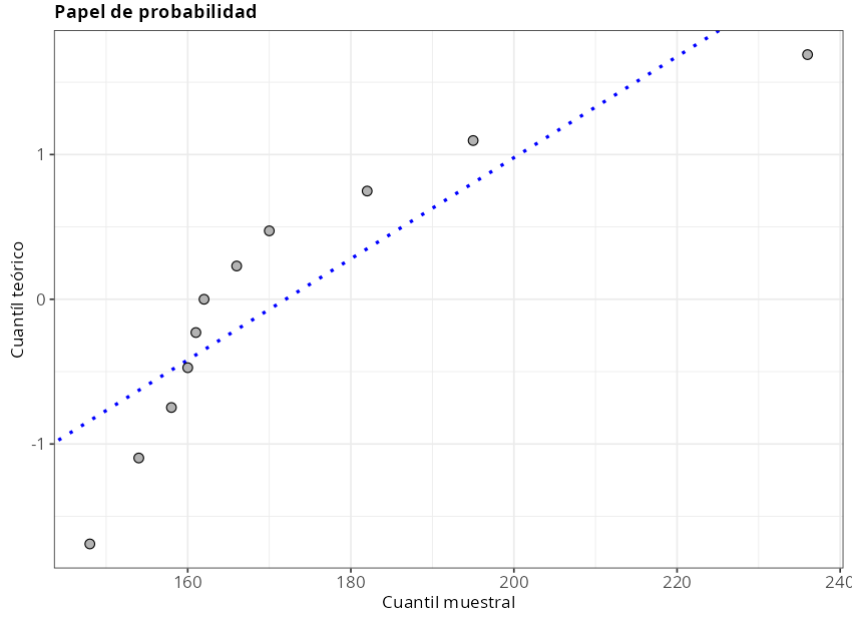
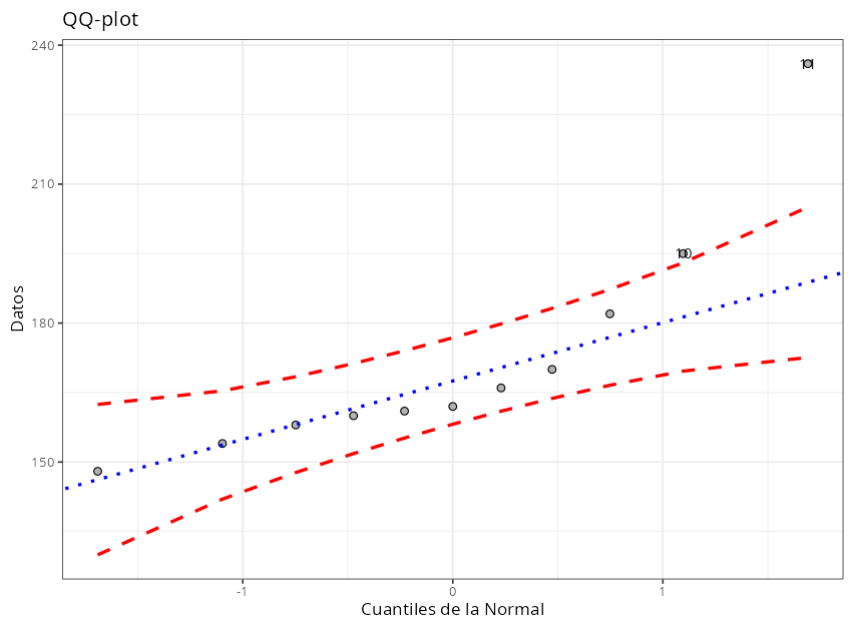
Como los P valores son inferiores al 5%, para todas las pruebas, rechazamos la hipótesis de normalidad. Así, con un nivel de confianza del 95%, tenemos evidencia de que los datos no siguen una distribución normal.
El gráfico de Probabilidad y el diagrama QQ-plot muestran que los datos no siguen una distribución normal, ya que no están alineados en una línea recta. Por lo tanto, se puede concluir que el conjunto de datos no representa una distribución normal.