2. Prueba de Media: Dos Muestras independientes
La prueba t puede ser usado para comparar las médias de dos muestras independentes.
Ejemplo 1:
Queremos probar la igualdad de las medias de dos poblaciones que tienen varianzas iguales. Se obtuvo una muestra de cada población, como se muestra en las siguientes tablas.
| Grupos | Muestra |
|---|---|
| Población 1 | 18,8 |
| Población 1 | 20,504 |
| Población 1 | 18,621 |
| Población 1 | 19,919 |
| Población 1 | 21,117 |
| Población 1 | 17,591 |
| Población 1 | 18,756 |
| Población 1 | 18,977 |
| Población 1 | 20,308 |
| Población 1 | 18,899 |
| Población 1 | 20,835 |
| Población 1 | 17,527 |
| Población 1 | 17,078 |
| Población 1 | 17,62 |
| Población 1 | 21,426 |
| Población 1 | 19,169 |
| Población 1 | 19,29 |
| Población 1 | 22,059 |
| Población 1 | 18,585 |
| Población 1 | 17,89 |
| Población 1 | 18,755 |
| Población 1 | 19,203 |
| Población 1 | 18,419 |
| Población 1 | 20,764 |
| Población 1 | 21,055 |
| Población 2 | 22,284 |
| Población 2 | 21,901 |
| Población 2 | 25,302 |
| Población 2 | 22,447 |
| Población 2 | 22,771 |
| Población 2 | 22,057 |
| Población 2 | 22,881 |
| Población 2 | 17,968 |
| Población 2 | 23,382 |
| Población 2 | 21,043 |
| Población 2 | 22,629 |
| Población 2 | 22,86 |
| Población 2 | 24,515 |
| Población 2 | 22,426 |
| Población 2 | 21,203 |
| Población 2 | 24,62 |
| Población 2 | 22,058 |
| Población 2 | 23,15 |
| Población 2 | 22,787 |
| Población 2 | 24,009 |
| Población 2 | 21,491 |
| Población 2 | 22,699 |
| Población 2 | 24,662 |
| Población 2 | 21,983 |
| Población 2 | 21,917 |
| Población 2 | 21,198 |
| Población 2 | 22,909 |
| Población 2 | 23,327 |
| Población 2 | 24,534 |
| Población 2 | 21,152 |
Se hará un upload de los datos para el sistema.
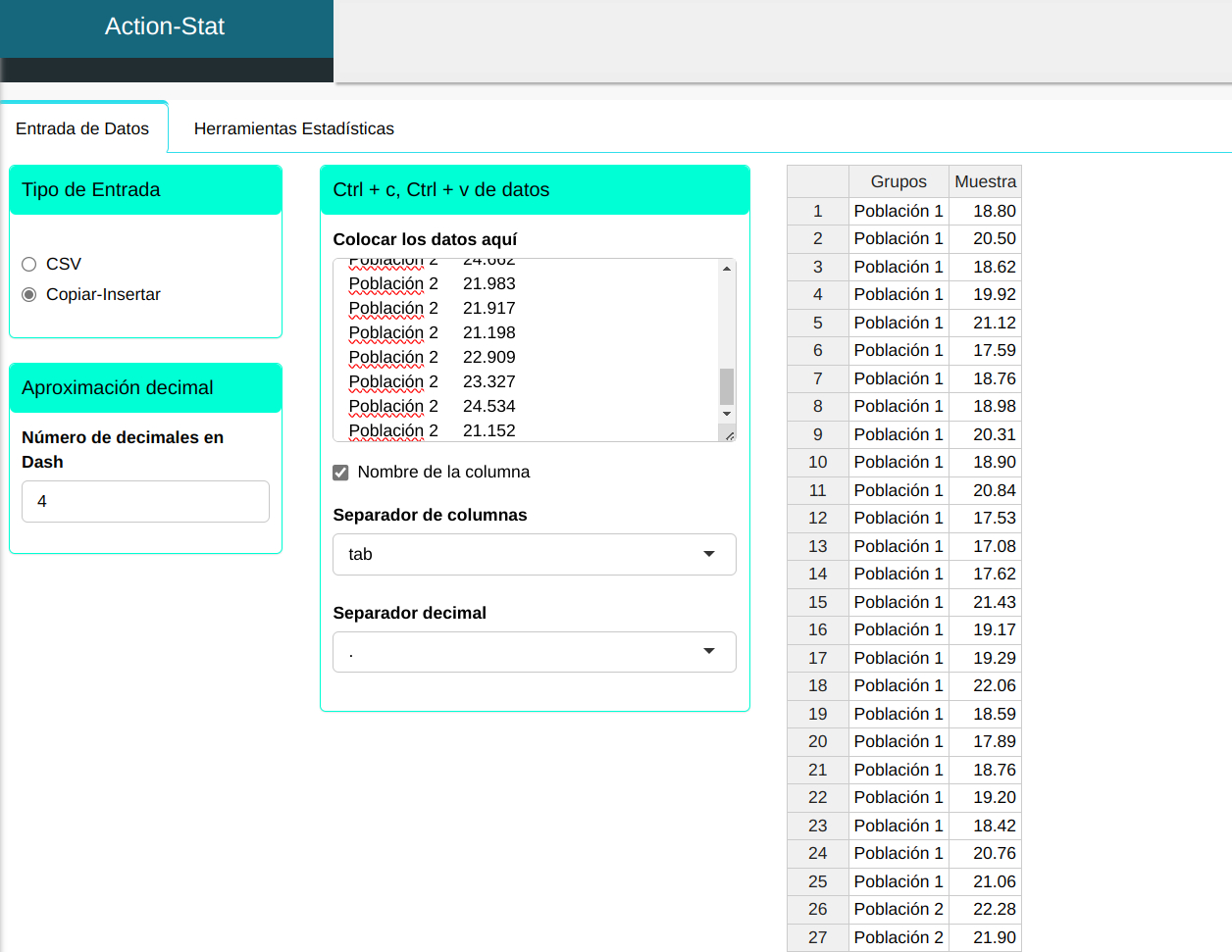
Para realizar la prueba de dos medias es elaborado conforme la configuración que se muestra en la figura de abajo.
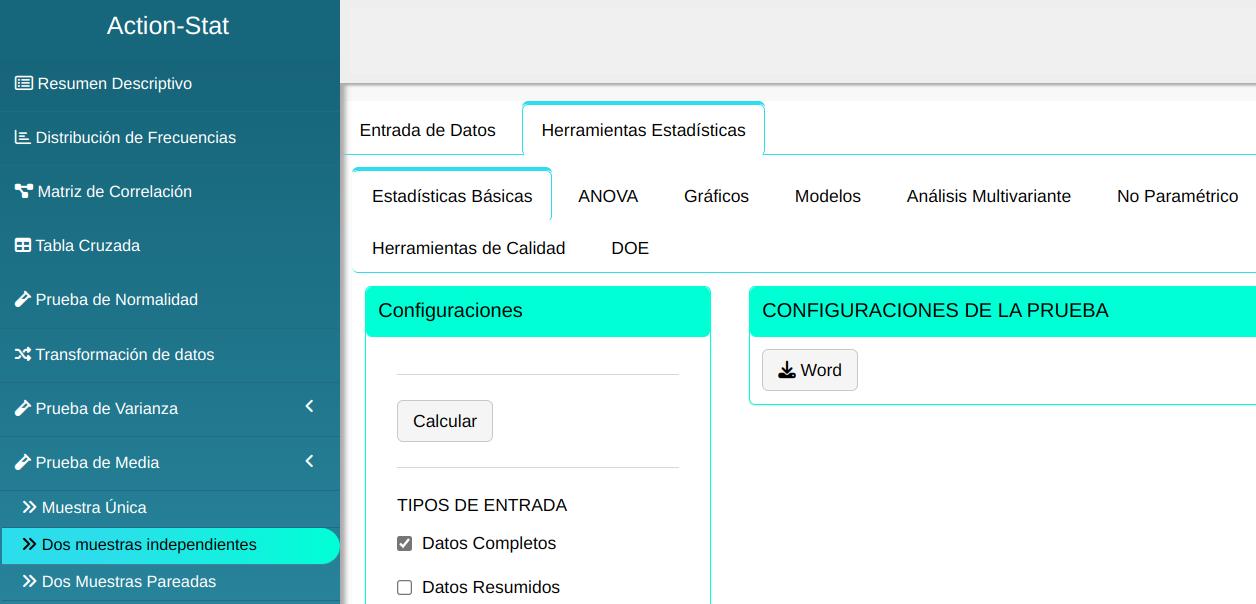
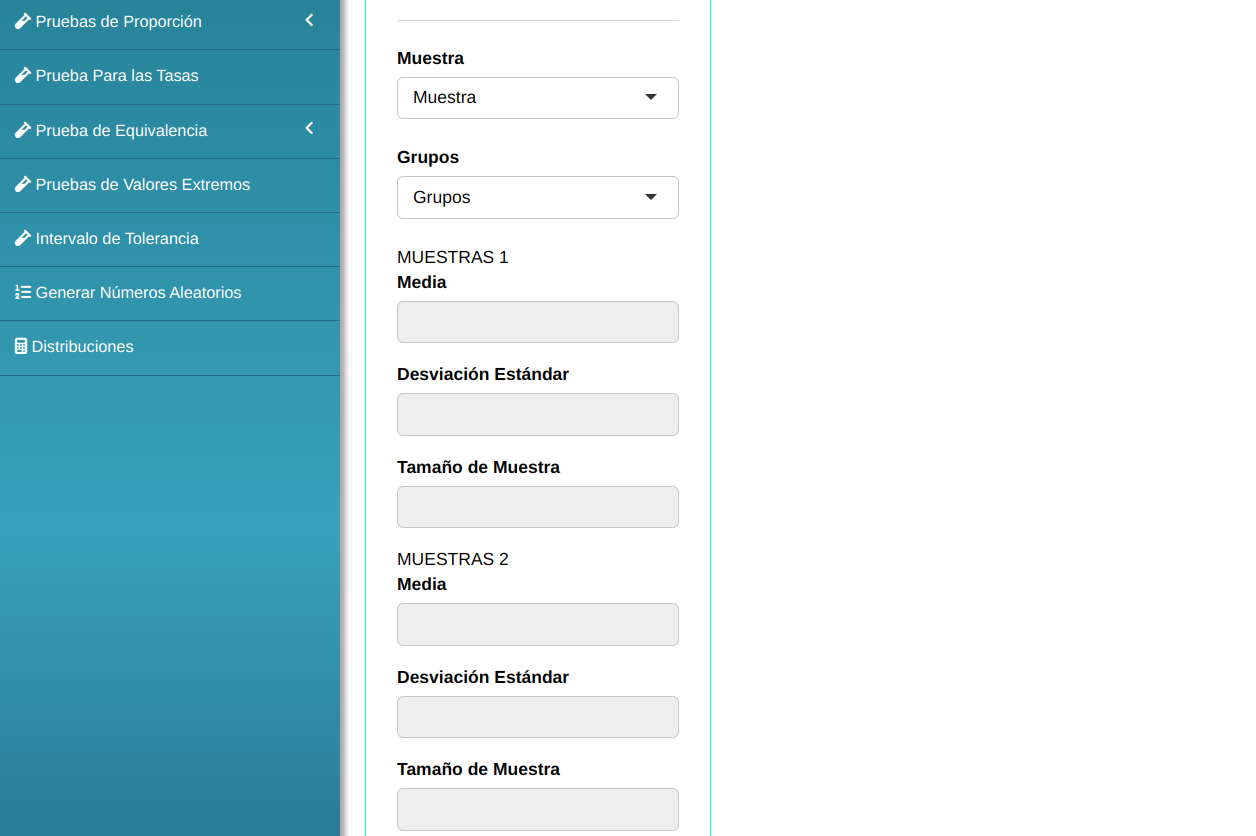
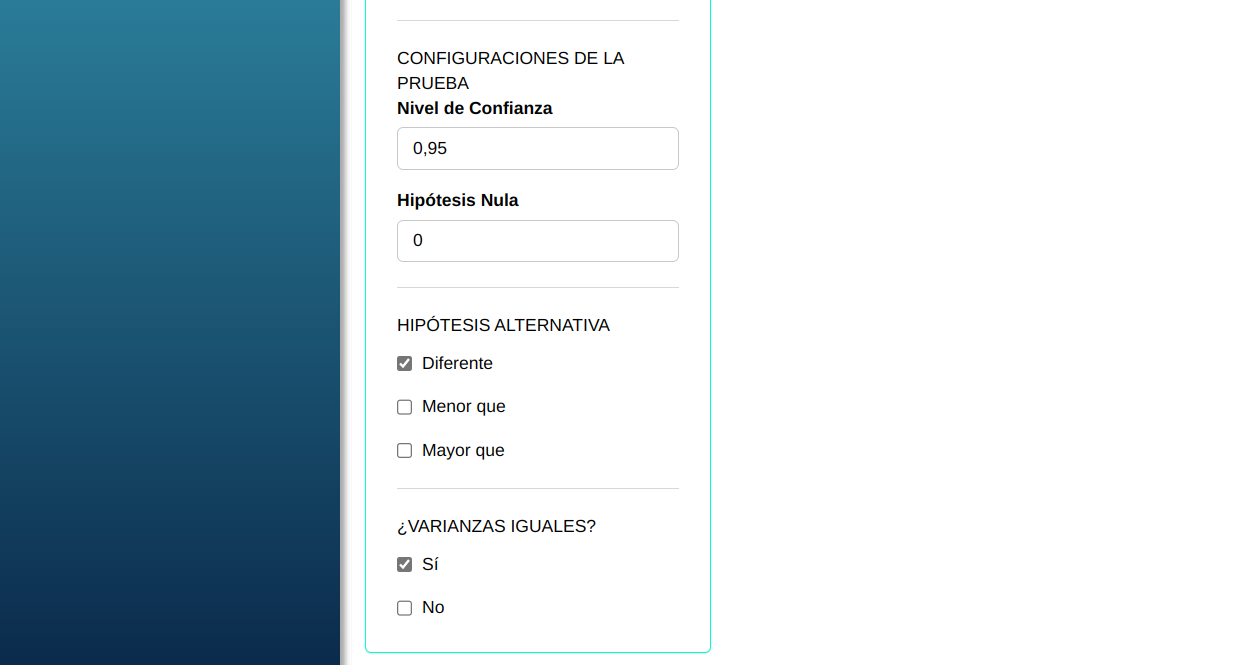
En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:
Resultados
| Valores | |
|---|---|
| Estadística T | -8.621733 |
| Grados de Libertad | 53 |
| P-valor | 1.151931e-11 |
| Media de la Población 1 | 19.32668 |
| Media de la Población 2 | 22.6055 |
| Desviación Estándar de la Población 1 | 1.362278 |
| Desviación Estándar de la Población 2 | 1.43822 |
| Desviación estándar Agrupado | 1.40434 |
| Tamaño de la Población 1 | 25 |
| Tamaño de la Población 2 | 30 |
| Hipótesis Alternativa Diferente de | 0 |
| Nivel de Confianza | 95% |
| Límite Inferior | -4.041599 |
| Límite Superior | -2.516041 |
El estadístico de la prueba es -8.62. Como el P-valor es 1,15193E-11 entonces, a un nivel de significación del 5%, rechazamos la hipótesis nula de que las medias de las dos poblaciones son iguales.
Ejemplo 2:
Queremos probar la igualdad de las medias de dos poblaciones que tienen varianzas iguales. Se tomó una muestra de cada población, como se muestra en las tablas siguientes.
| Medias | Desviación Estándar | Tamaño de la muestra | |
|---|---|---|---|
| Muestra 1 | 19.32668 | 1.362277802 | 25 |
| Muestra 2 | 22.6055 | 1.438220326 | 30 |
Para realizar la prueba de dos medias es elaborado conforme la configuración que se muestra en la figura de abajo.
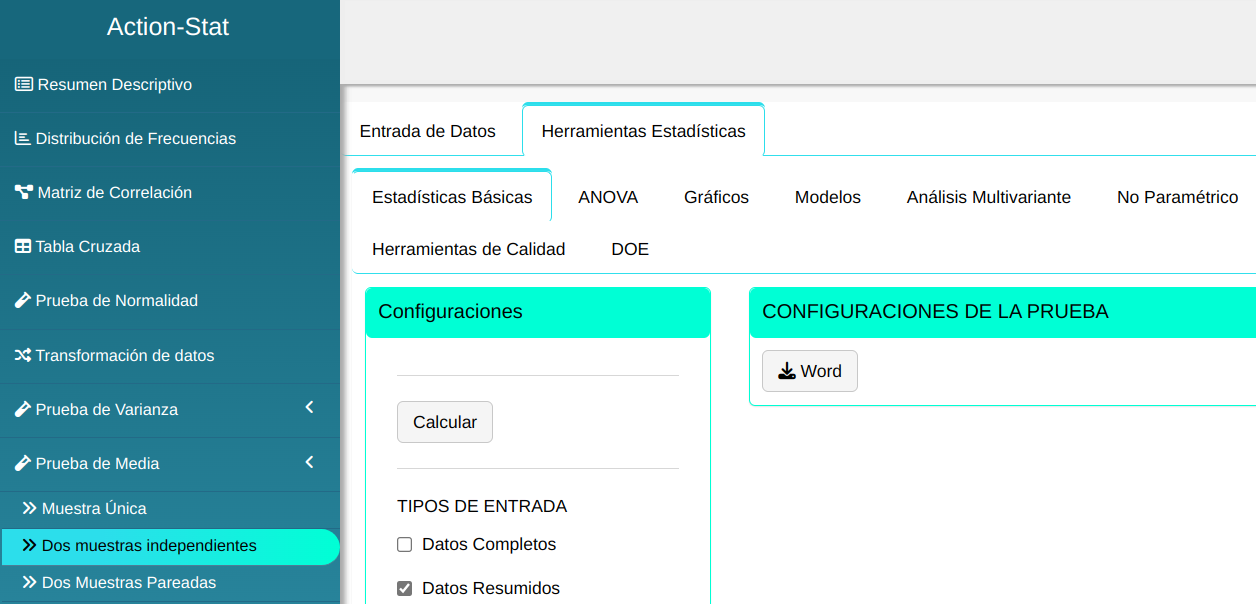
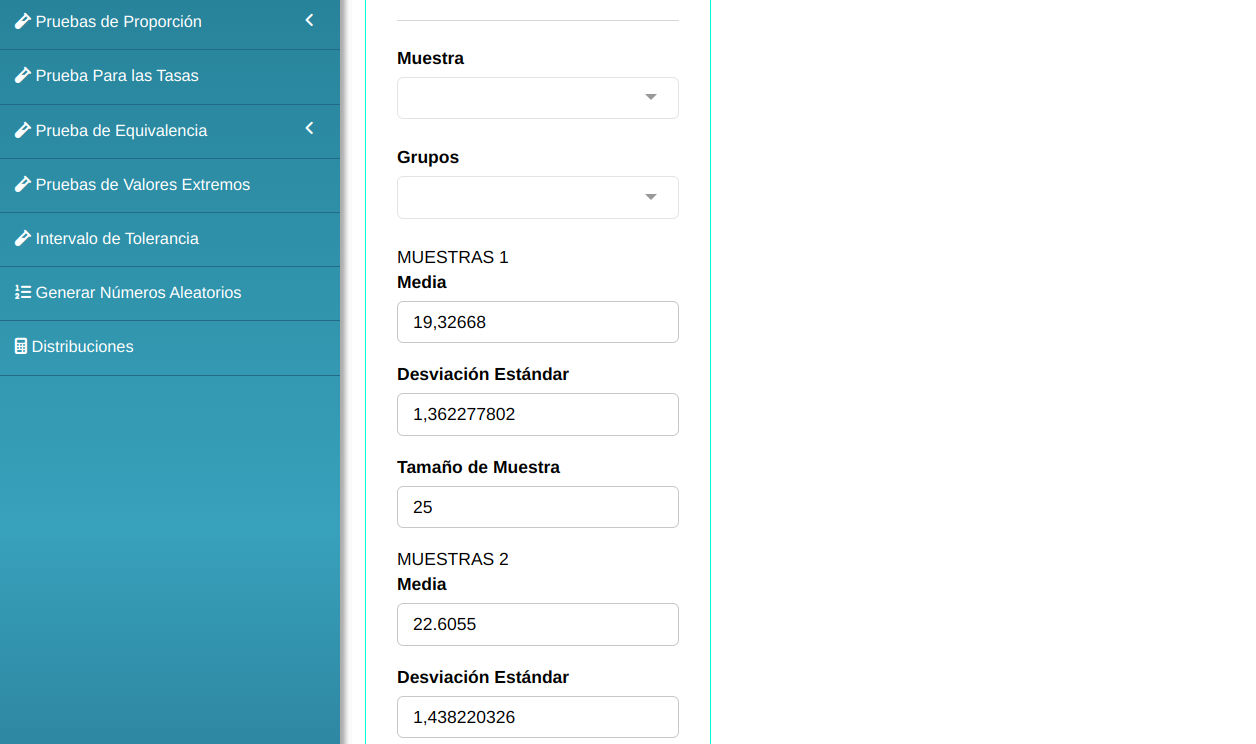
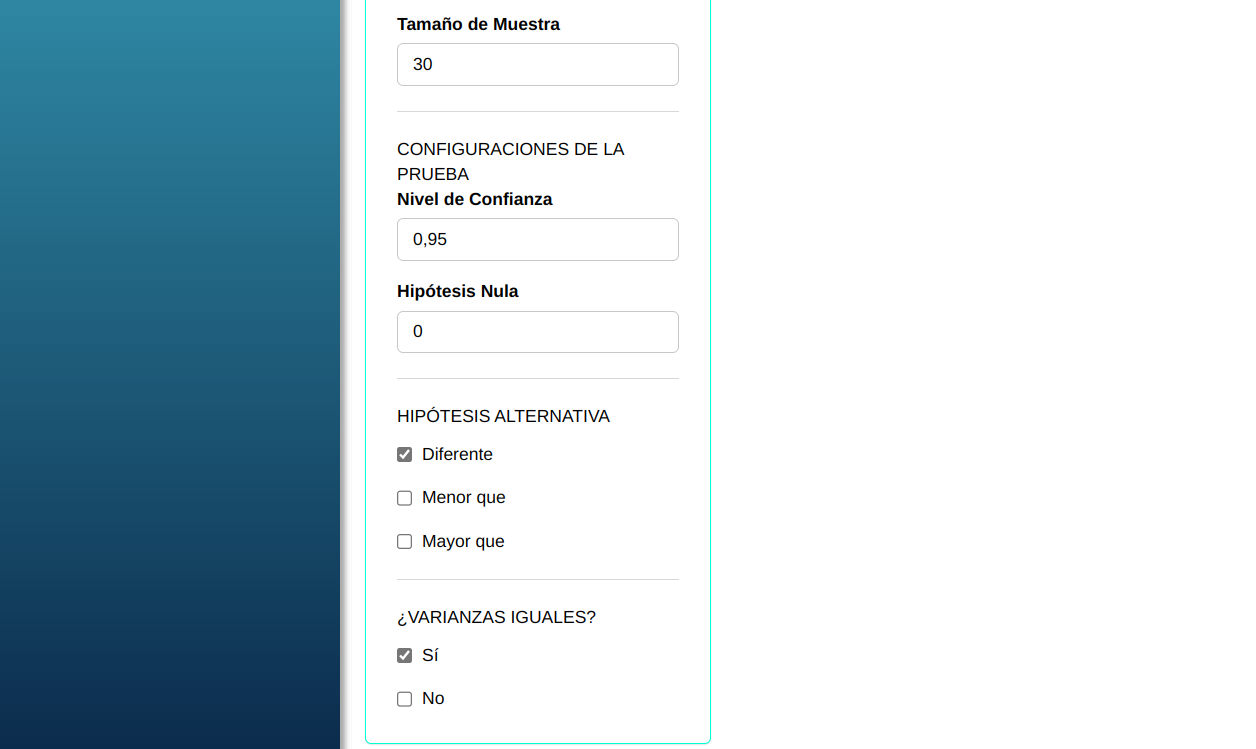
En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:
Resultados
| Valores | |
|---|---|
| Estadística T | -8.621733 |
| Grados de Libertad | 53 |
| P-valor | 1.151931e-11 |
| Media de la Muestra 1 | 19.32668 |
| Media de la Muestra 2 | 22.6055 |
| Desviación Estándar de la Muestra 1 | 1.362278 |
| Desviación Estándar de la Muestra 2 | 1.43822 |
| Desviación Estándar Agrupado | 1.40434 |
| Tamaño de la Muestra 1 | 25 |
| Tamaño de la Muestra 2 | 30 |
| Hipótesis Alternativa Diferente de | 0 |
| Nivel de Confianza | 95% |
| Límite Inferior | -4.041599 |
| Límite Superior | -2.516041 |
El estadístico de la prueba es -8.62. Como el P-valor es 1.15E-11, a un nivel de significancia de 5%, se rechaza la hipótesis nula de que las medias de las dos poblaciones son iguales.