3. Prueba de medias: Dos muestras pareadas
La prueba t pareada comprobará la media de las diferencias entre dos muestras independientes.
Ejemplo:
Consideremos una muestra de mediciones del laboratorio de la empresa A y una muestra de mediciones del laboratorio de la empresa B, valores que se puede encontrar en la siguiente tabla. Las pruebas de ambos laboratorios se llevan a cabo en el mismo patrón, por lo tanto, existe una correlación entre ellos, es decir, las muestras son dependientes. Evaluar la compatibilidad de mediciones entre el laboratorio de la empresa A y el laboratorio de la empresa B.
| LAB A | LAB B |
|---|---|
| 1.00552 | 0.01942 |
| -1.49928 | -0.46512 |
| 0.21367 | 0.53218 |
| 0.44658 | -0.14844 |
| 0.62766 | -0.60021 |
| 0.31091 | 0.06495 |
| -0.83878 | 0.33013 |
| -0.29054 | 0.12116 |
| -0.08487 | 0.74269 |
| -1.26465 | -1.64232 |
| -0.06353 | 0.05497 |
| -1.07632 | 0.76342 |
| -1.34134 | 1.74131 |
| -0.55062 | -0.06392 |
| 1.61848 | -1.88146 |
| 0.50997 | -0.76135 |
| 0.76027 | -0.23009 |
| 0.68061 | -1.16800 |
| -1.91464 | 0.88392 |
| -0.20072 | 0.96512 |
Subiremos los datos al sistema.
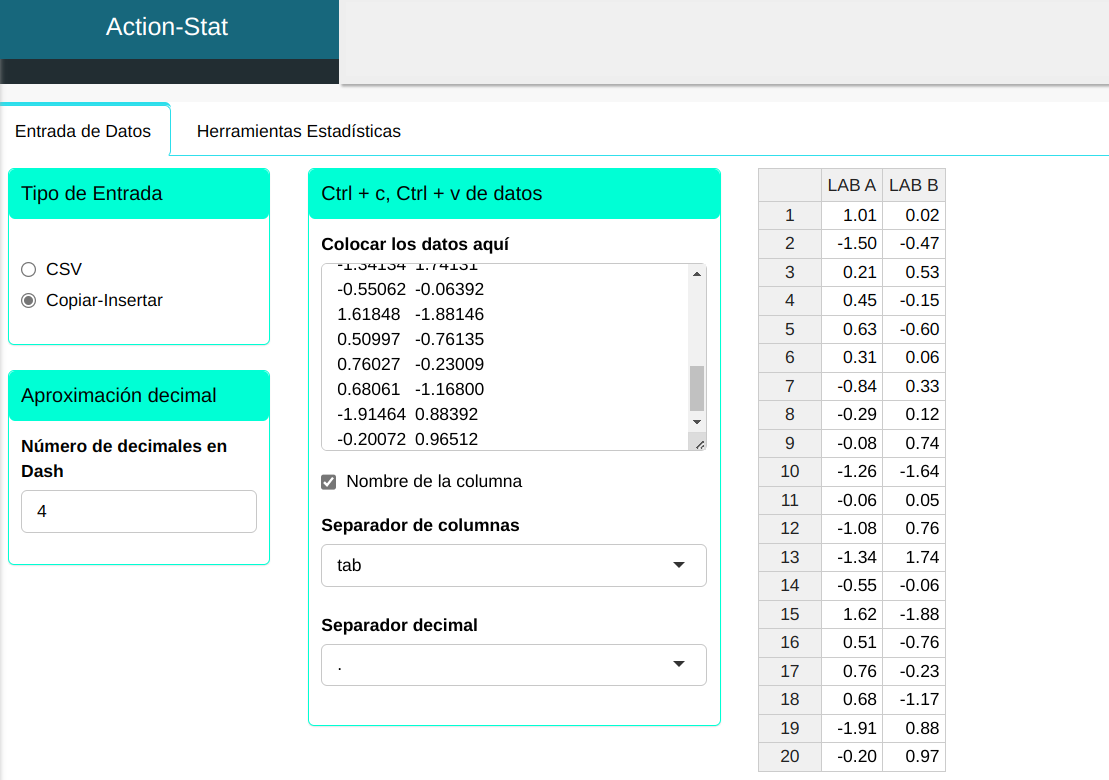
A continuación se realiza la prueba.
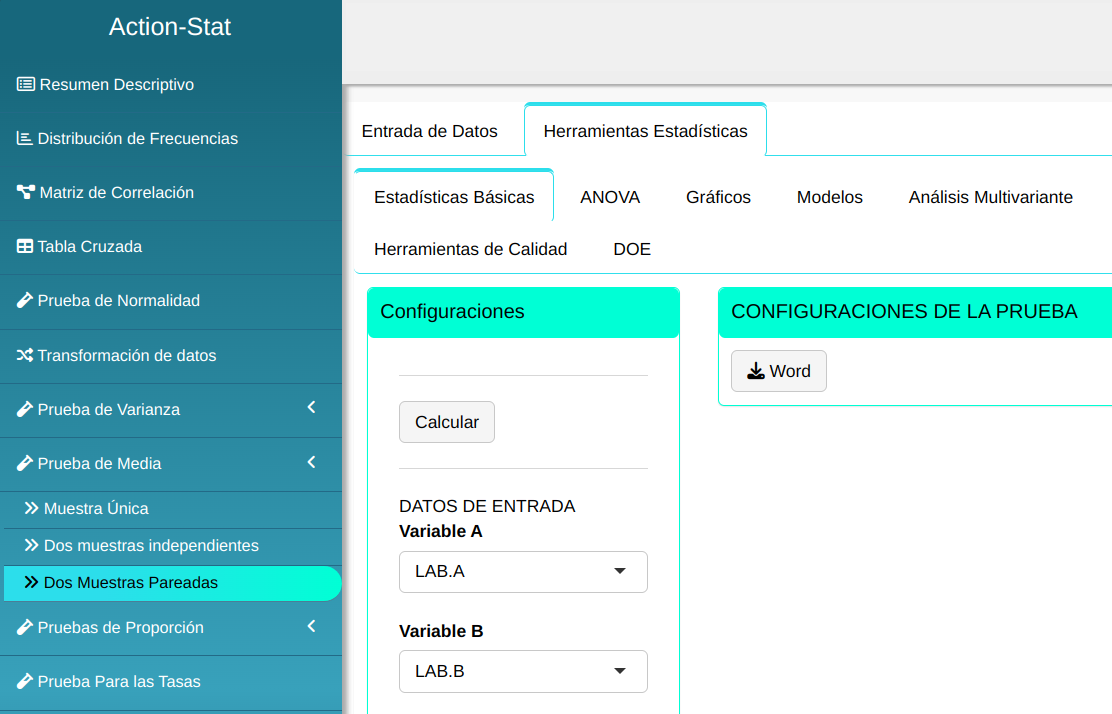
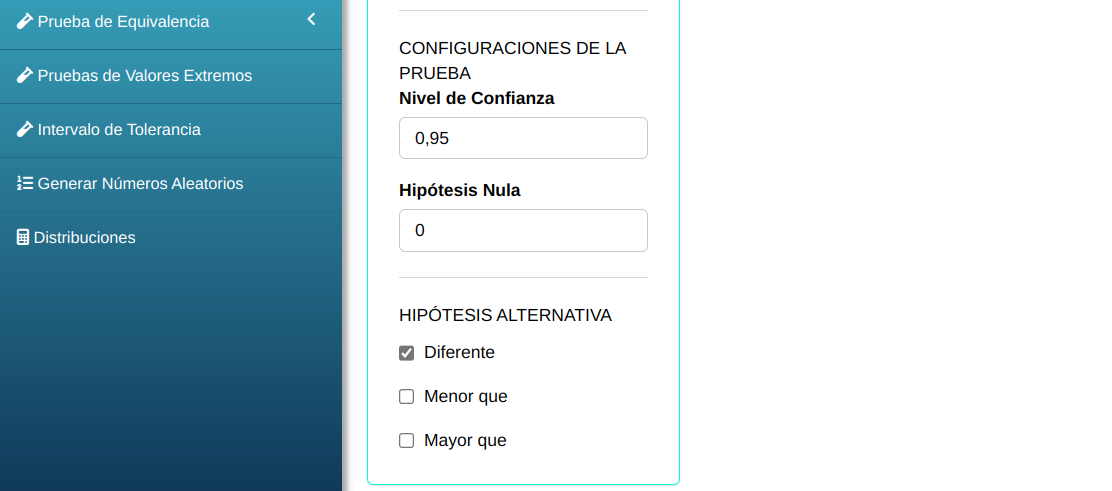
Clicando en Calcular obtenemos los resultados. También se puede generar y descargar los resultados en un archivo Word.

Los resultados son:
Resultados
| Valores | |
|---|---|
| Estadística T | -0.3149009 |
| Grados de libertad | 19 |
| P-valor | 0.756269 |
| Media de LAB.A | -0.14757 |
| Media de LAB.B | -0.037085 |
| Desviación estándar de las diferencias | 1.569077 |
| Tamaño de la muestra | 20 |
| Hipótesis alternativa diferente de | 0 |
| Nivel de confianza | 95% |
| Límite inferior | -0.8448358 |
| Límite superior | 0.6238658 |
El estadístico de prueba es -0.3149887. Como el P-valor es 0.7562, a un nivel de significancia del 5%, no rechazamos la hipótesis nula de que las mediciones entre el laboratorio de la empresa A y el laboratorio de la empresa B sean compatibles.