1. Proporciones: Muestra única
La prueba de proporción se utiliza para analizar si la tasa de éxito de un experimento es satisfactorio.
Ejemplo:
Un fabricante garantiza que el 90% de las piezas que suministra a la línea de producción de una determinada fábrica cumplen las especificaciones requeridas. Se seleccionó una muestra de 200 piezas y cada una de ellas se evaluó como dentro de especificación (valor 1) o fuera de especificación (valor 0) según la tabla siguiente. A un nivel del 5%, ¿podemos afirmar que la afirmación del fabricante es cierta?
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 0 |
| 1 |
A continuación cargaremos los datos al sistema.
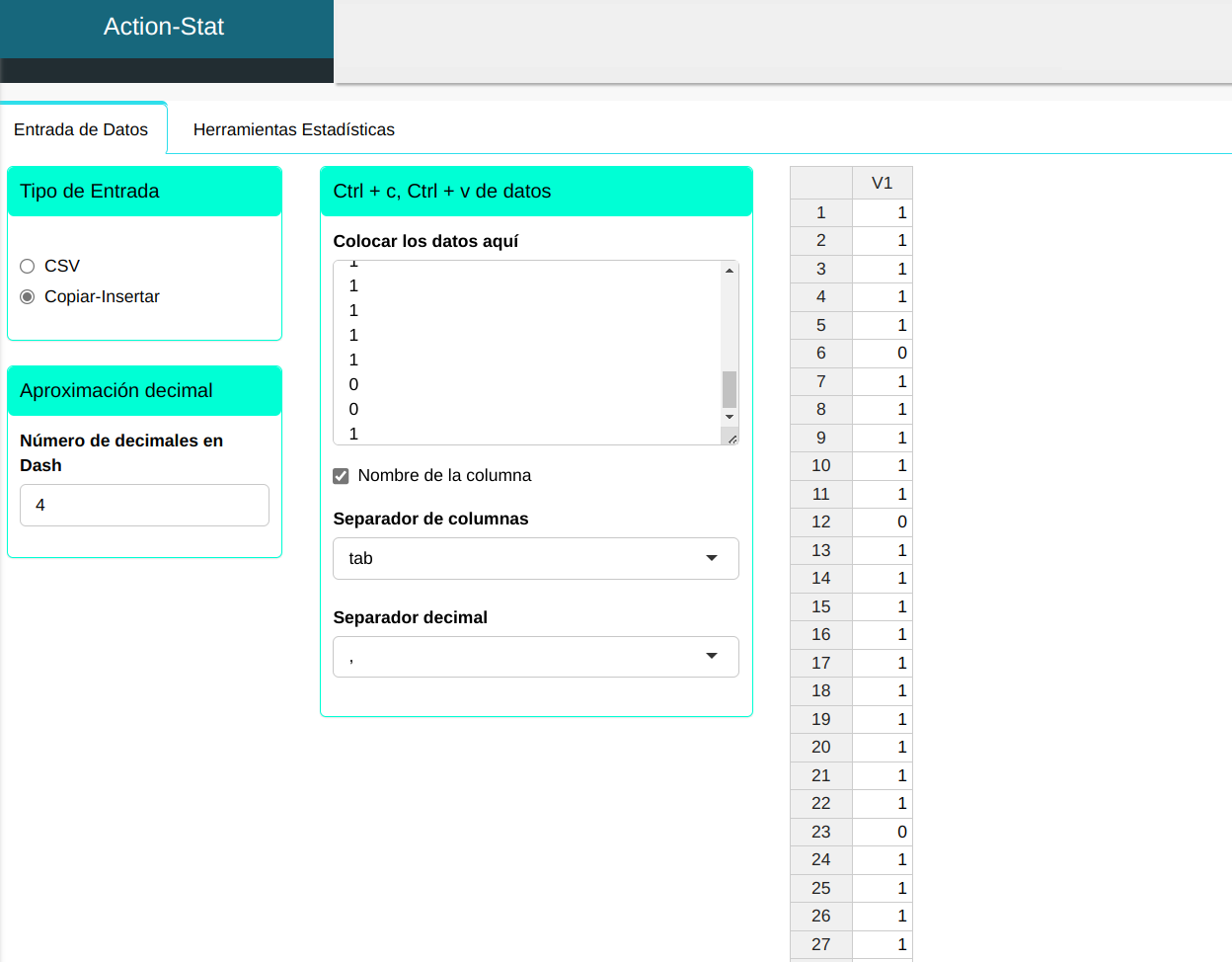
Haremos el Test de Proporciones.

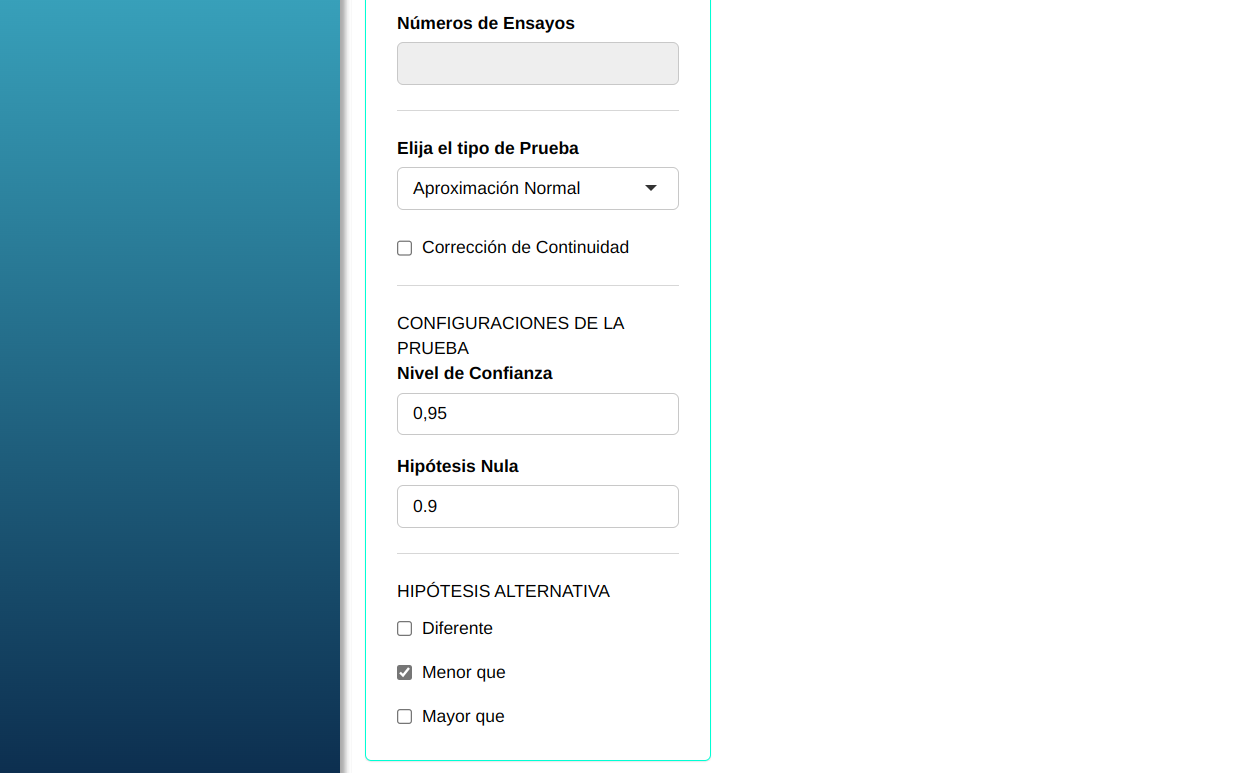
Clicando en Calcular obtenemos los resultados. También se puede generar y descargar los resultados en un archivo Word.

Los resultados son:
Resultados
| Cantidad | Proporciones | |
|---|---|---|
| Éxito | 175 | 0.875 |
| Fracaso | 25 | 0.125 |
Resultados
| Valores | |
|---|---|
| Z Estadísticas | -1.178511 |
| P-valor | 0.1192964 |
| Proporción de éxito en la muestra | 0.875 |
| Hipótesis alternativa Menor que | 0.9 |
| Nivel de confianza | 95% |
| Límite inferior | 0 |
| Límite superior | 0.9134655 |
La estadística de prueba es -1.178511. Como el valor P es 0.1192964 > 0.05 Entonces, a un nivel de significancia del 5%, tenemos evidencia de que la proporción es igual a 0.9.
Ejemplo 2:
Un fabricante garantiza que el 90% de las piezas que suministra a la línea de producción de una determinada fábrica se ajusta a las especificaciones requeridas. El análisis de una muestra de 200 piezas reveló que 25 estaban defectuosas. Con un nivel del 5%, ¿podemos afirmar que la afirmación del fabricante es cierta?
Haremos la prueba de proporciones.
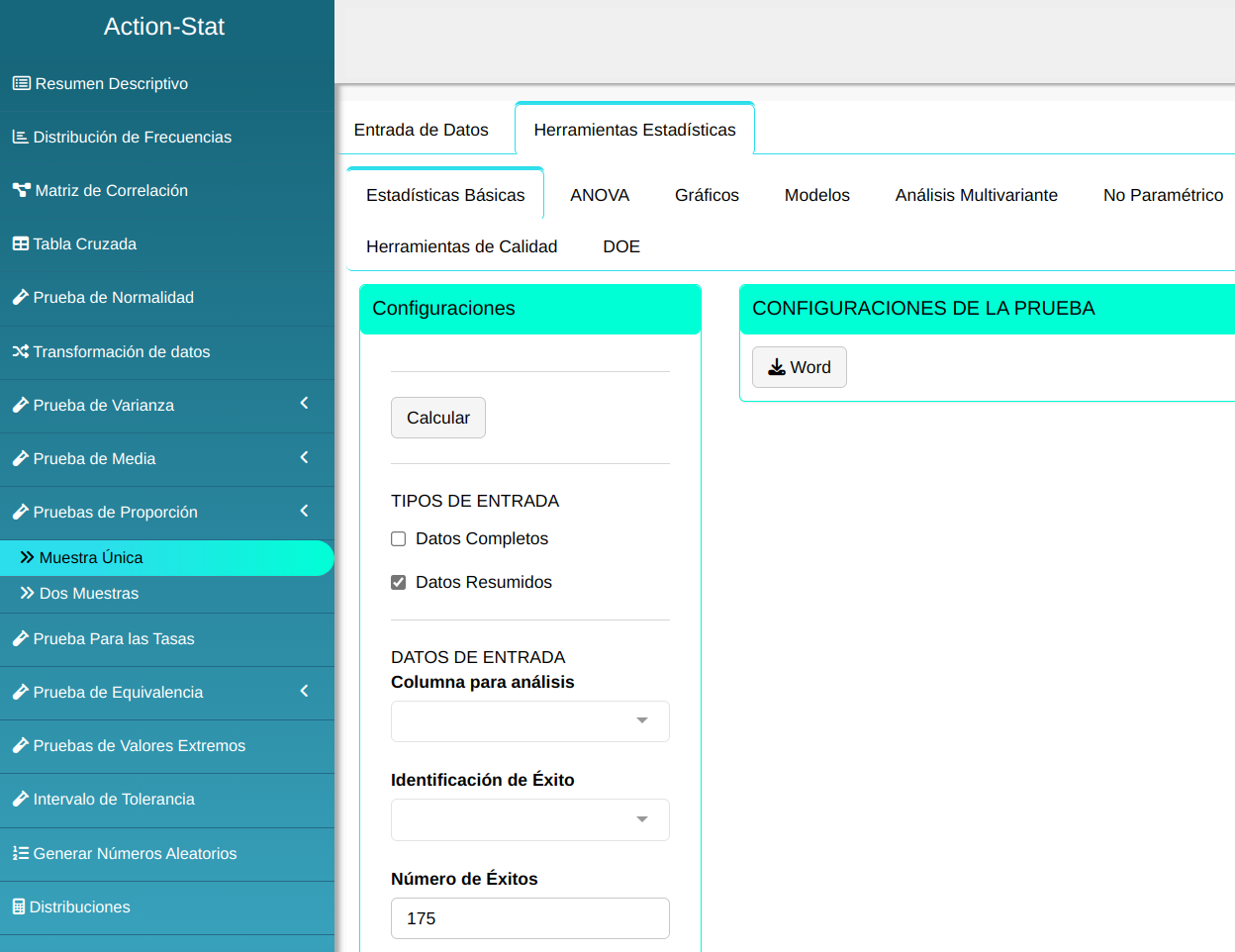
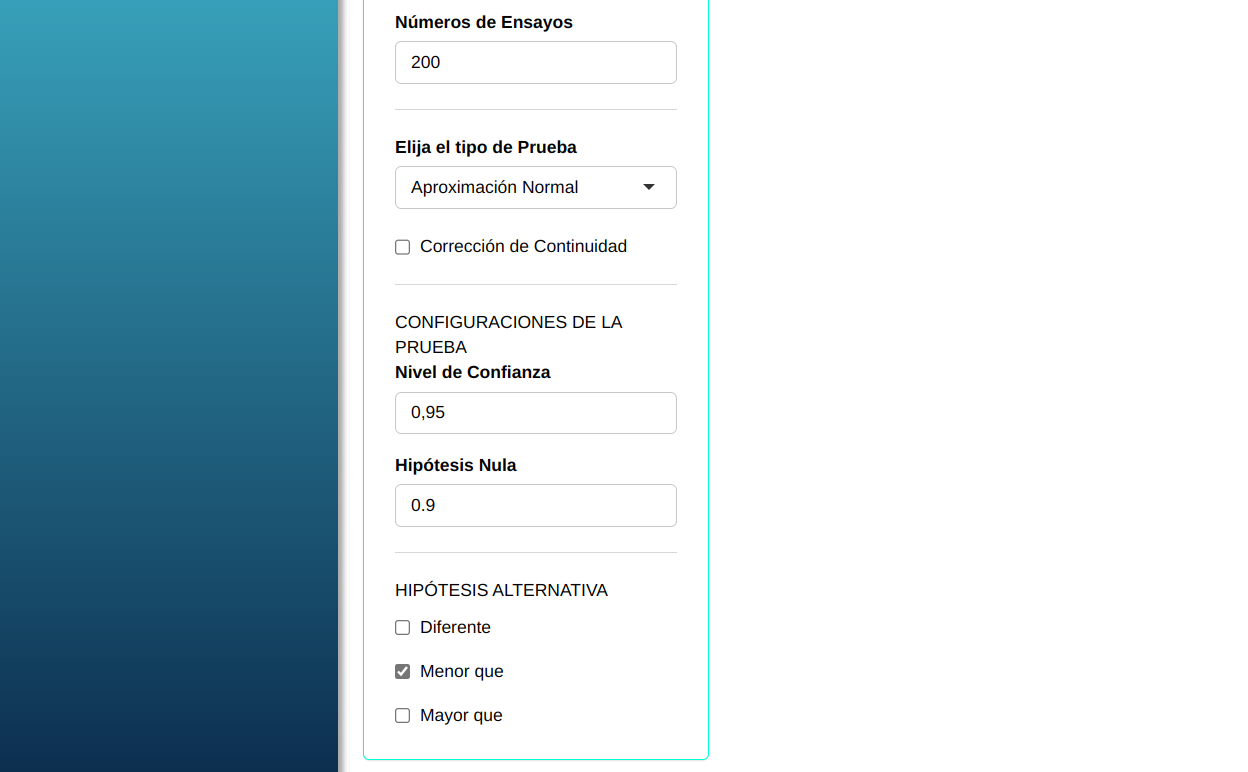
Clicando en Calcular obtenemos los resultados. También se puede generar y descargar los resultados en un archivo Word.

Los resultados son:
Resultados
| Cantidad | Proporciones | |
|---|---|---|
| Éxito | 175 | 0.875 |
| Fracaso | 25 | 0.125 |
Resultados
| Valores | |
|---|---|
| Estadísticas Z | -1.178511 |
| P-valor | 0.1192964 |
| Proporción de éxito en la muestra | 0.875 |
| Hipótesis alternativa Menor que | 0.9 |
| Nivel de confianza | 95% |
| Límite inferior | 0 |
| Límite superior | 0.9134655 |
La estadística de prueba es -1.178511. Como el P-valor es 0.1192964 > 0.05 Entonces, a un nivel de significancia del 5%, tenemos evidencia de que la proporción es igual a 0.9.