2. Proporciones: dos muestras
La prueba de proporciones de dos muestras se utiliza para comparar la tasa de éxito de los experimentos.
Ejemplo 1:
Una empresa que presta servicios de asesoramiento económico a otras empresas está interesada en comparar el índice de reclamaciones sobre sus servicios en dos de sus oficinas en dos ciudades diferentes. Supongamos que la empresa ha seleccionado al azar 100 servicios realizados por la oficina de la ciudad A y 120 servicios realizados por la oficina de la ciudad B. Las tablas muestran estos servicios (1 indica que no hay reclamaciones y 0 que hay reclamaciones). La empresa quiere saber si estos resultados son suficientes para concluir que las dos oficinas tienen una diferencia significativa entre sus índices de reclamaciones. Vamos a subir los datos en el sistema.
| Grupo | Valor |
|---|---|
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 1 |
| Muestra 1 | 0 |
| Muestra 1 | 0 |
| Muestra 1 | 0 |
| Muestra 1 | 0 |
| Muestra 1 | 0 |
| Muestra 1 | 0 |
| Muestra 1 | 0 |
| Muestra 1 | 0 |
| Muestra 1 | 0 |
| Muestra 1 | 0 |
| Muestra 1 | 0 |
| Muestra 1 | 0 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 1 |
| Muestra 2 | 0 |
| Muestra 2 | 0 |
| Muestra 2 | 0 |
| Muestra 2 | 0 |
| Muestra 2 | 0 |
| Muestra 2 | 0 |
| Muestra 2 | 0 |
| Muestra 2 | 0 |
| Muestra 2 | 0 |
| Muestra 2 | 0 |
| Muestra 2 | 0 |
| Muestra 2 | 0 |
| Muestra 2 | 0 |
| Muestra 2 | 0 |
| Muestra 2 | 0 |
| Muestra 2 | 0 |
| Muestra 2 | 0 |
| Muestra 2 | 0 |
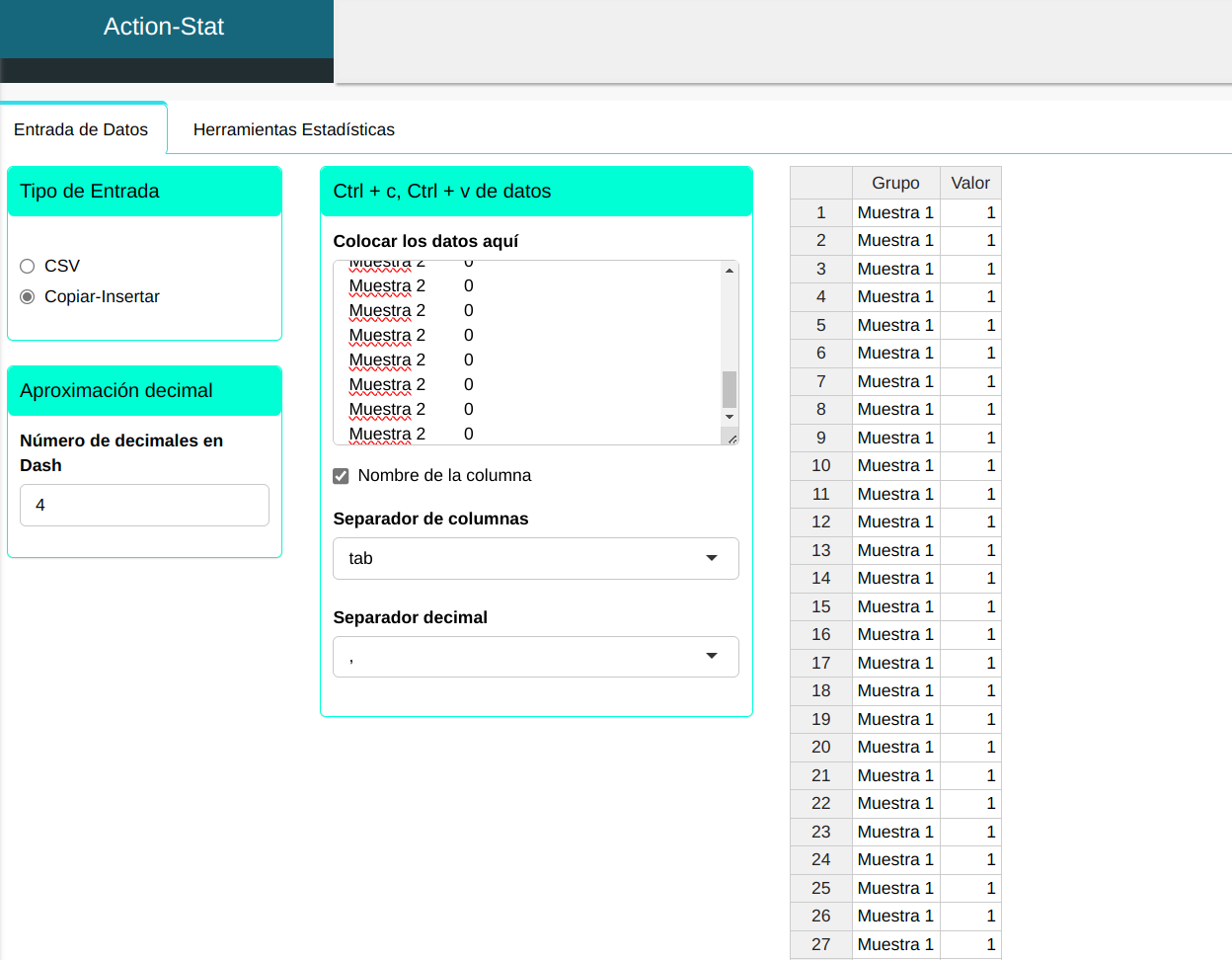
Para realizar una prueba de proporciones, se realiza la siguiente configuración que se muestra en la figura siguiente.


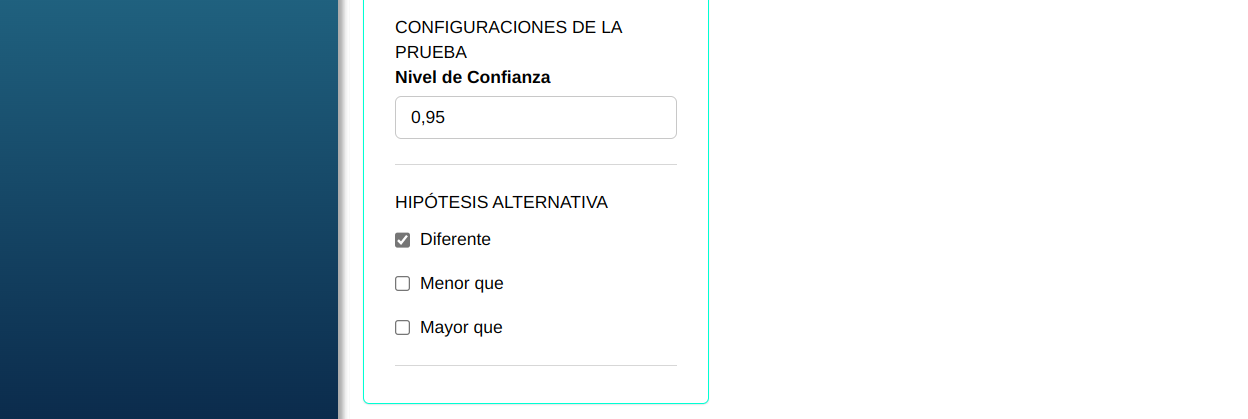
En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:
Resultados - Muestra 1
| Cantidad | Proporciones | |
|---|---|---|
| Éxito | 88 | 0.88 |
| Fracaso | 12 | 0.12 |
Resultados - Muestra 2
| Cantidad | Proporciones | |
|---|---|---|
| Éxito | 102 | 0.85 |
| Fracaso | 18 | 0.15 |
Resultados - Aproximación normal
| Valores | |
|---|---|
| Estadísticas Z | 0.6456331 |
| P-valor | 0.518517 |
| Proporción de éxito en Muestra 1 | 0.88 |
| Proporción de éxito en Muestra 2 | 0.85 |
| Hipótesis alternativa | Diferente de 0 |
| Nivel de confianza | 95% |
| Límite inferior | -0.06021159 |
| Límite superior | 0.1202116 |
Como el P-valor obtenido, 0.518517, es mayor que el nivel de significancia adoptado, de 0.05, no podemos rechazar la hipótesis nula, de igualdad entre proporciones. Por lo tanto, no hay evidencia para decir que las oficinas presenten una diferencia significativa entre sus tasas de reclamaciones.
Ejemplo 2:
Una empresa que presta servicios de asesoramiento económico a otras empresas está interesada en comparar el índice de reclamaciones sobre sus servicios en dos de sus oficinas en dos ciudades diferentes Supongamos que la empresa ha seleccionado al azar 100 servicios realizados por la oficina de la ciudad A y ha comprobado que 12 de ellos han recibido algún tipo de reclamación. De la oficina de la ciudad B, se han seleccionado 120 servicios y 18 han recibido algún tipo de reclamación. La empresa quiere saber si estos resultados son suficientes para concluir que las dos oficinas tienen una diferencia significativa entre sus índices de reclamaciones.
Para realizar la prueba de proporciones, se realiza la siguiente configuración que se muestra en la figura siguiente.



En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:
Resultados - Conjunto de datos 1
| Cantidad | Proporciones | |
|---|---|---|
| Éxito | 88 | 0.88 |
| Fracaso | 12 | 0.12 |
Resultados - Conjunto de datos 2
| Cantidad | Proporciones | |
|---|---|---|
| Éxito | 102 | 0.85 |
| Fracaso | 18 | 0.15 |
Resultados - Aproximación normal
| Valores | |
|---|---|
| Estadísticas Z | 0.6456331 |
| P-valor | 0.518517 |
| Proporción de éxito en la muestra 1 | 0.88 |
| Proporción de éxito en la muestra 2 | 0.85 |
| Hipótesis alternativa | Diferente de 0 |
| Nivel de confianza | 95% |
| Límite inferior | -0.06021159 |
| Límite superior | 0.1202116 |
Como el P-valor obtenido, 0.518517, es mayor que el nivel de significancia adoptada, 0.05, por lo que no rechazamos la hipótesis nula, de igualdad entre proporciones. Por lo tanto, no hay evidencia para decir que las oficinas presenten una diferencia significativa entre sus tasas de reclamaciones.