1. Prueba de varianza: una varianza
La prueba de Chi-cuadrado se utiliza para analizar si la varianza del conjunto de los datos son diferentes del valor esperado.
Detalles:
La prueba de una varianza supone que el conjunto de datos tiene una distribución normal. La hipótesis nula y la hipótesis alternativa se establecen en función de la varianza de la población (o desviación estándar de la población).
Ejemplo 1:
El peso de los componentes mecánicos producidos por una empresa determinada es una variable aleatoria que se supone que tiene una distribución normal. El objetivo es estudiar la variabilidad en el peso de los componentes antes mencionados. Para ello se ha obtenido una muestra de tamaño 11. cuyos datos serán subidos.
| 98 |
| 97 |
| 102 |
| 100 |
| 98 |
| 101 |
| 102 |
| 105 |
| 95 |
| 102 |
| 100 |
Los datos serán subidos.
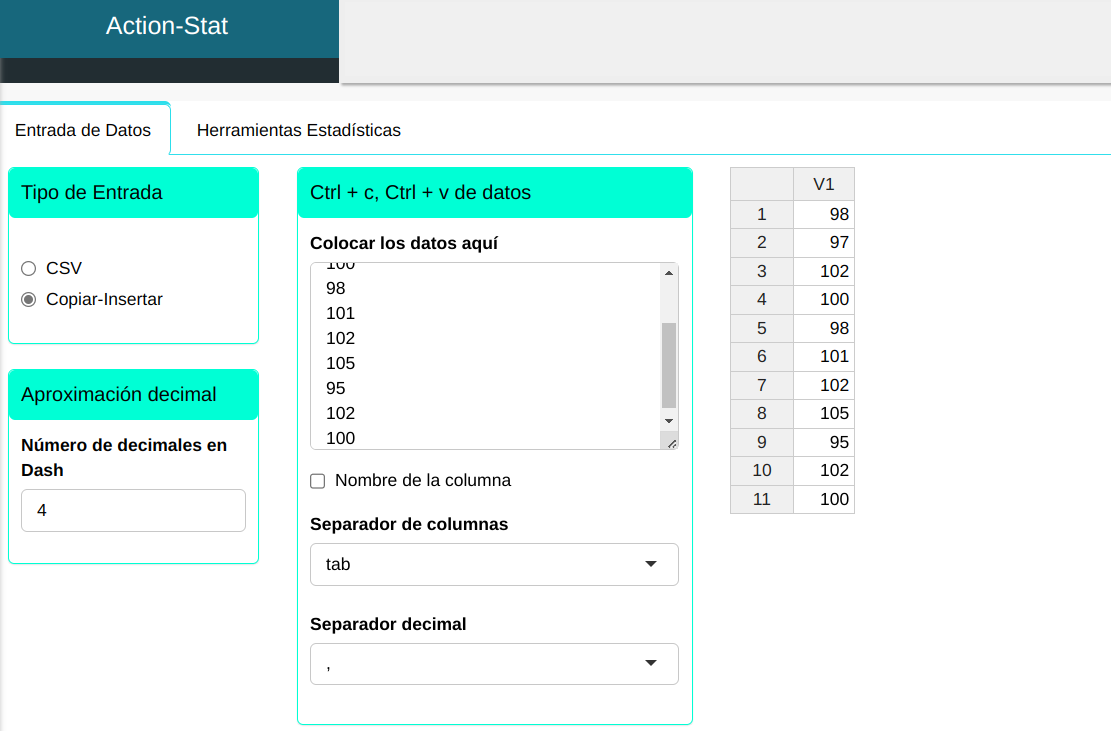
Para realizar prueba de varianza es elaborado conforme la configuración que se muestra en la figura de abajo.
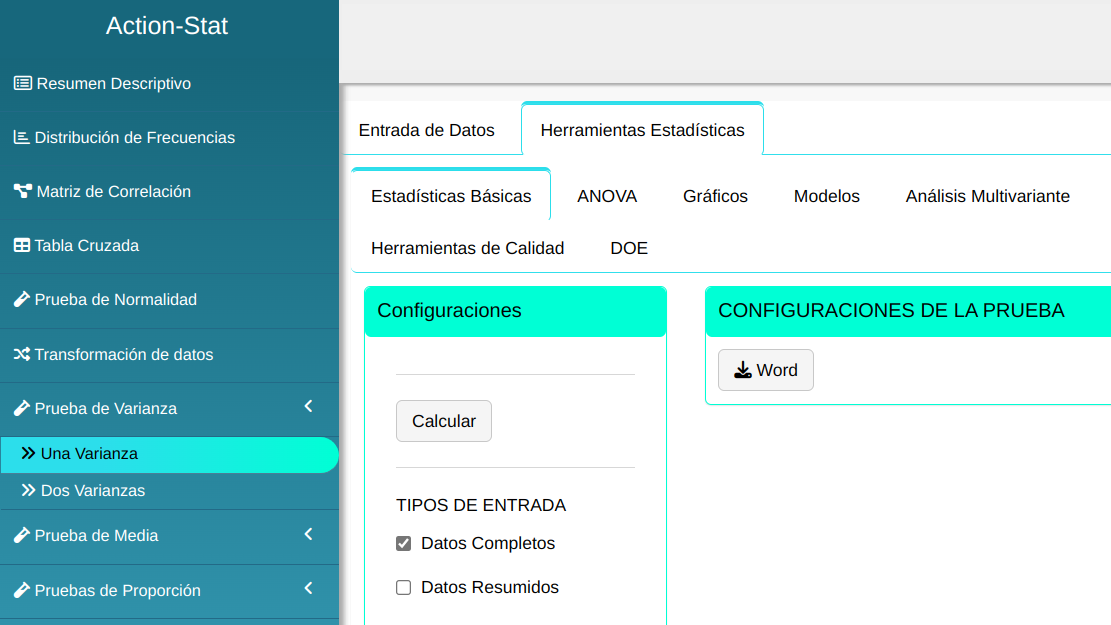
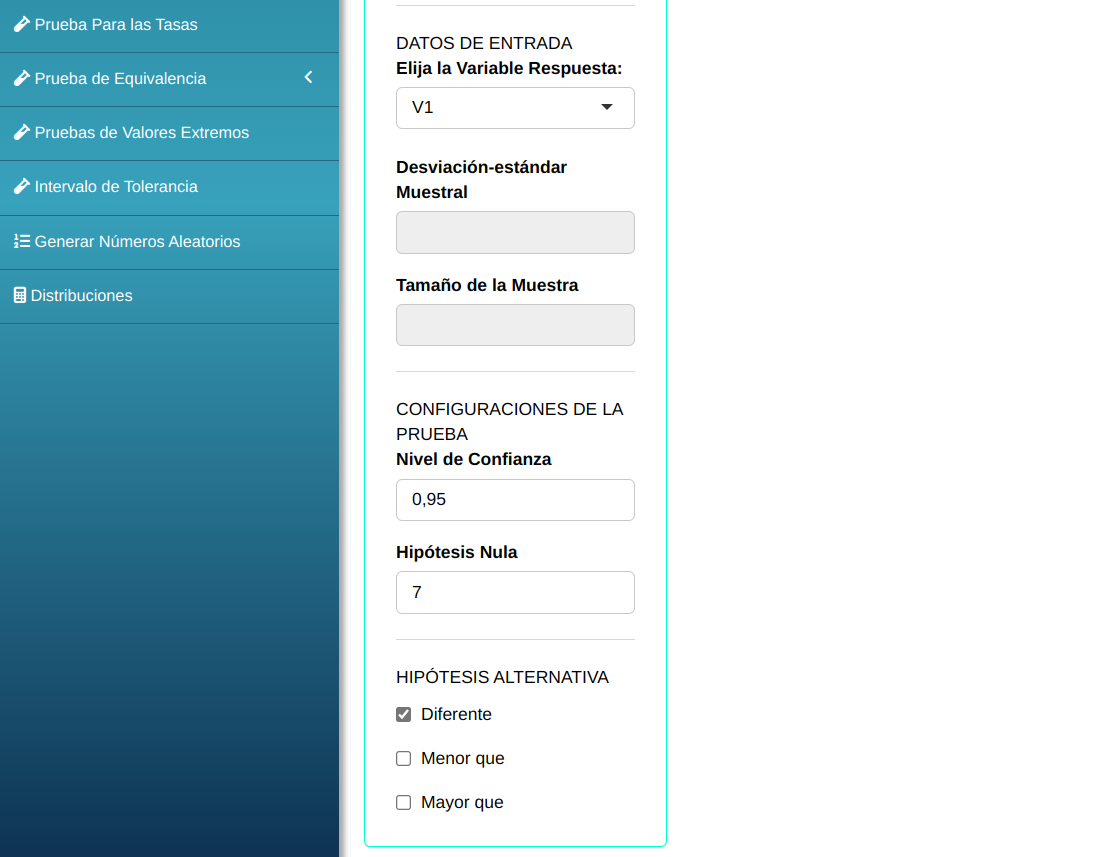
Clique em Calcular para visualizar os resultados e baixá-los em formato Word.

Los resultados son:
Prueba de una varianza
| Valor | |
|---|---|
| Grados de libertad | 10 |
| Estadísticas de chi-cuadrado | 11.4285 |
| P-valor | 0.6502338 |
| Varianza de la muestra | 8 |
| Tamaño de la muestra | 11 |
| Hipótesis alternativa: Diferente | 7 |
| Nivel de confianza | 95% |
| Límite inferior | 3.905644 |
| Límite superior | 24.63833 |
Como el P-valor es 0.65 > 0.05 entonces, al nivel de significancia de 5%, No rechazamos la hipótesis nula de que la varianza de los datos es igual a 7. El intervalo de confianza del 95% para la varianza viene dado por CI = (3.9056;24.6383).
Ejemplo 2:
Una máquina llenadora automática es utiliza para llenar botellas con detergente líquido. En una muestra aleatoria de 20 botellas, la varianza muestral del volumen de llenado fue $s^2$ = 0.0153 $(\text{onza fluida})^2$. Si la varianza del volumen de llenado supera 0.01 $(\text{onza fluida})^2$, habrá una proporción inaceptable de botellas que no se llenaron completamente o que se llenaron en exceso. ¿Existen evidencias en los datos de la muestra que sugieran que el fabricante tiene un problema con botellas con falta o exceso de detergente? Utilice $ \alpha = 0.05 $ suponiendo que el volumen de llenados sigue una distribución normal. Considere también que se está realizando una prueba de hipótesis para la varianza con una hipótesis nula $\sigma^2 = 0.01 $.
Para realizar prueba de varianza es elaborado conforme la configuración que se muestra en la figura abajo.
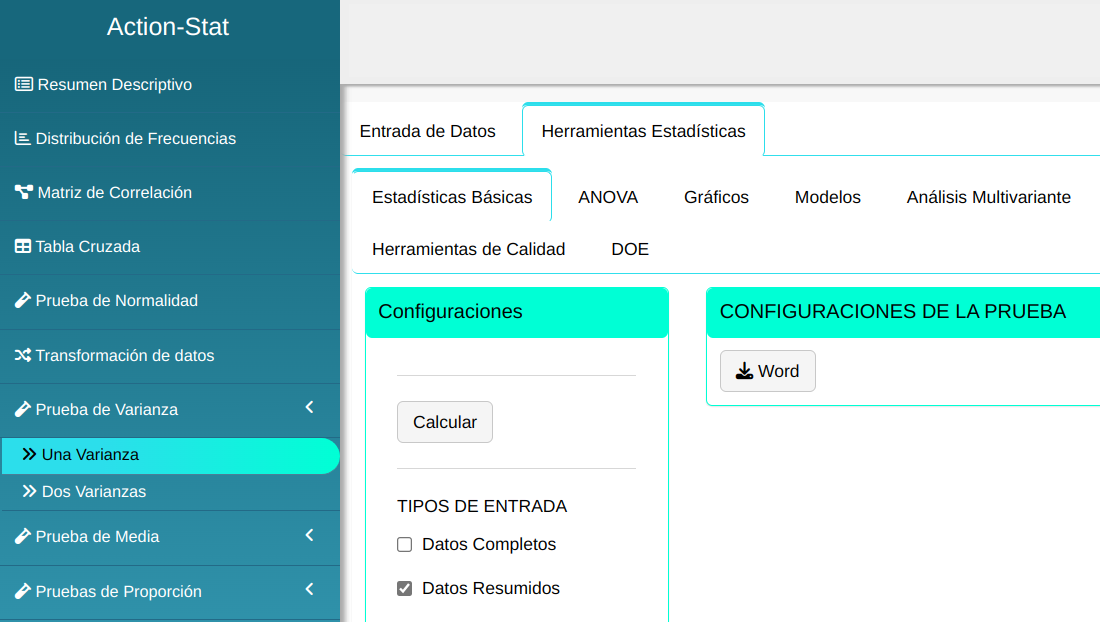
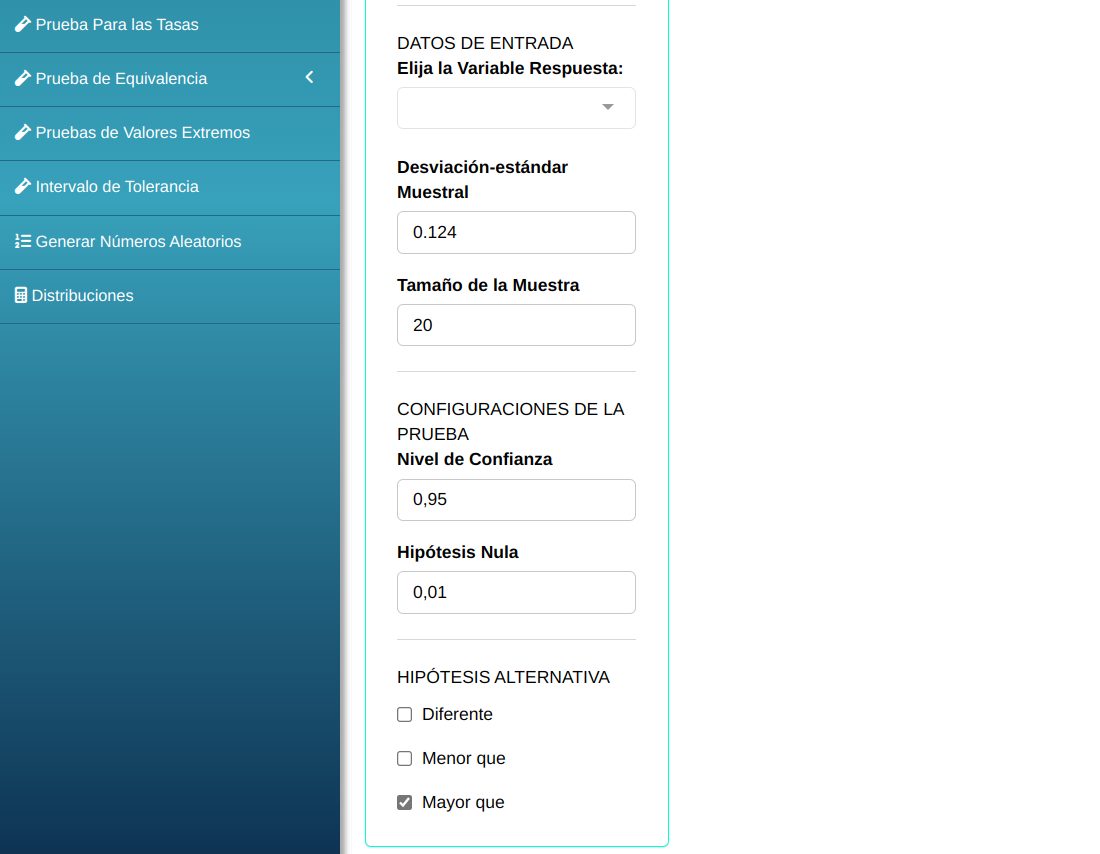
Haga un clic en calcular para visualizar los resultados y descargarlos en un documento de Word.

Los resultados son:
Prueba de una varianza
| Valor | |
|---|---|
| Grados de libertad | 19 |
| Estadísticas de chi-cuadrado | 29.2144 |
| P-valor | 0.06268668 |
| Varianza de la muestra | 0.015376 |
| Tamaño de la muestra | 20 |
| Hipótesis alternativa: Mayor que | 0.01 |
| Nivel de confianza | 95% |
| Límite inferior | 0.009691766 |
| Límite superior | inf |
Como el P-valor es igual a 0.06268668 > 0.05 = 5%, no rechazamos la hipótesis nula. En otras palabras, tenemos evidencia de que la varianza no excede el valor de 0.01.