2. Prueba de varianza: dos varianzas
La prueba F se utiliza para analizar la varianza entre dos conjuntos de datos diferentes y compararlos mediante pruebas de hipótesis.
Ejemplo 1:
Un analista de calidad quiere evaluar si existe diferencia en las medidas de eje de comandos desarrollados por dos sistemas mecanizados. La siguiente tabla presenta las medidas de dos poblaciones de dos sistemas que son independientes y tienen distribución normal. Con un nivel de confianza de 95% de confianza, ¿existe una diferencia significativa entre la variabilidad de las mediciones del eje de comando de dos sistemas mecanizado?
| Sistema Mecanizado | Eje de Comando |
|---|---|
| Sistema 1 | 18.7997 |
| Sistema 1 | 20.5035 |
| Sistema 1 | 18.6214 |
| Sistema 1 | 19.9192 |
| Sistema 1 | 21.117 |
| Sistema 1 | 18.7545 |
| Sistema 1 | 19.2026 |
| Sistema 1 | 18.4187 |
| Sistema 1 | 20.7641 |
| Sistema 1 | 21.0553 |
| Sistema 1 | 19.1688 |
| Sistema 1 | 19.2898 |
| Sistema 1 | 22.059 |
| Sistema 1 | 18.5854 |
| Sistema 1 | 17.8896 |
| Sistema 1 | 20.8353 |
| Sistema 1 | 17.527 |
| Sistema 1 | 17.078 |
| Sistema 1 | 17.6197 |
| Sistema 1 | 21.4255 |
| Sistema 1 | 17.5905 |
| Sistema 1 | 18.7561 |
| Sistema 1 | 18.9772 |
| Sistema 1 | 20.3084 |
| Sistema 1 | 18.8988 |
| Sistema 2 | 21.1609 |
| Sistema 2 | 26.1371 |
| Sistema 2 | 21.4737 |
| Sistema 2 | 30.9934 |
| Sistema 2 | 22.8421 |
| Sistema 2 | 24.4133 |
| Sistema 2 | 20.4137 |
| Sistema 2 | 25.5475 |
| Sistema 2 | 21.8791 |
| Sistema 2 | 22.6706 |
| Sistema 2 | 24.7531 |
| Sistema 2 | 25.7219 |
| Sistema 2 | 22.6389 |
| Sistema 2 | 26.2308 |
| Sistema 2 | 26.7998 |
| Sistema 2 | 28.4708 |
| Sistema 2 | 26.9941 |
| Sistema 2 | 25.1489 |
| Sistema 2 | 24.6179 |
| Sistema 2 | 27.0194 |
| Sistema 2 | 25.0589 |
| Sistema 2 | 22.1119 |
| Sistema 2 | 20.3069 |
| Sistema 2 | 23.6758 |
| Sistema 2 | 27.1201 |
| Sistema 2 | 29.6136 |
| Sistema 2 | 25.9948 |
| Sistema 2 | 18.223 |
| Sistema 2 | 23.7336 |
| Sistema 2 | 22.4208 |
A continuación se hará un upload de los datos al sistema.
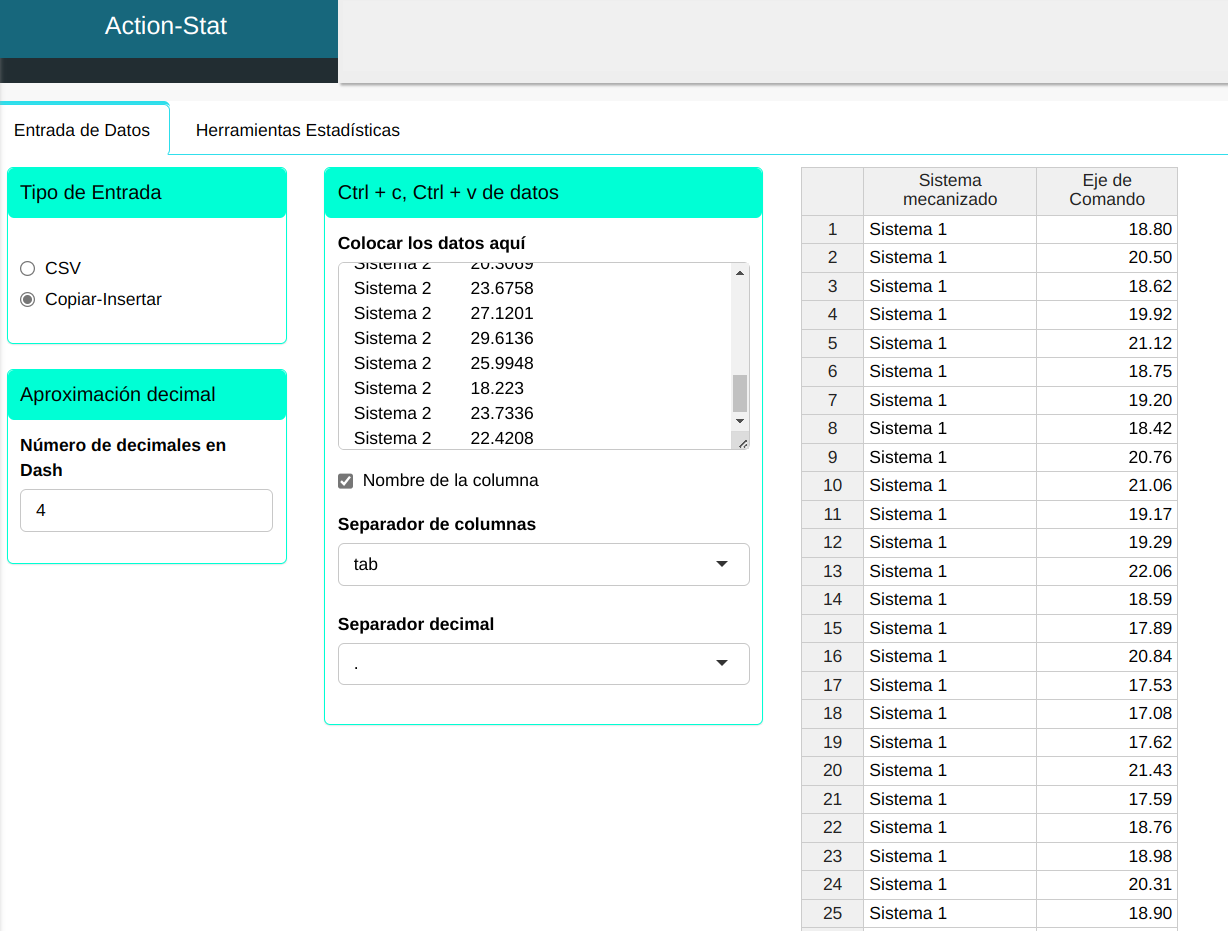
Para realizar una prueba de dos varianzas, se realiza la siguiente configuración como se muestra en la siguiente figura.
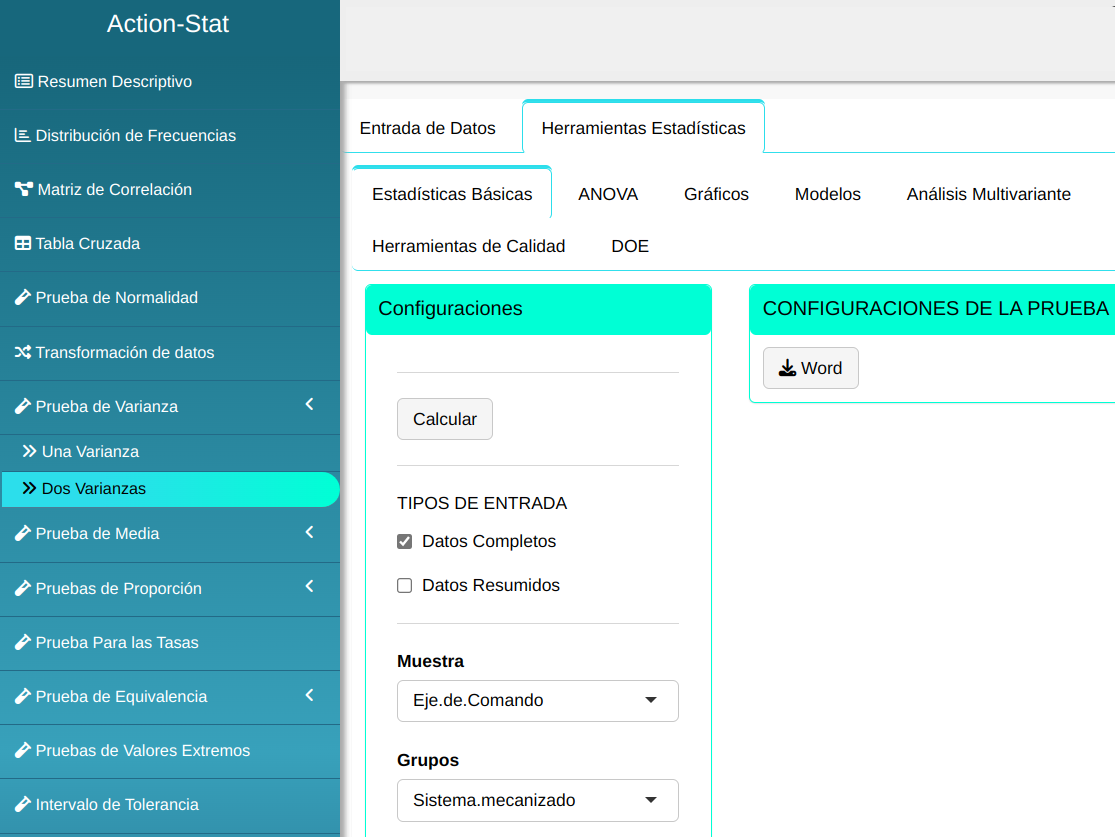
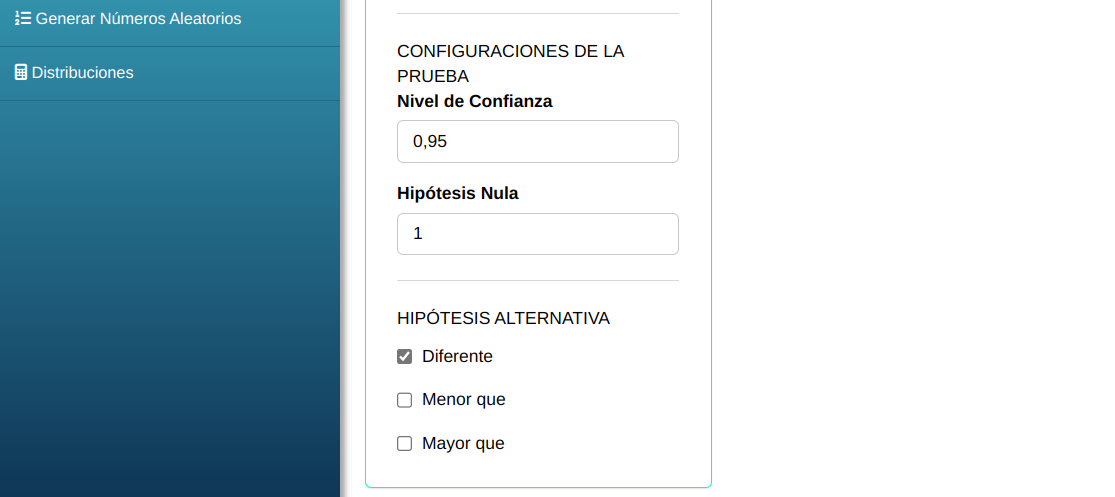
Clicando en Calcular obtenemos los resultados. También se puede generar y descargar los resultados en un archivo Word.

Los resultados son:
Prueba de Dos Varianzas
| Valores | |
|---|---|
| Estadística F | 0.222586 |
| Grados de libertad (Numerador) | 24 |
| Grados de libertad (Denominador) | 29 |
| P-Valor | 0.0003578537 |
| Desviación estándar-Sistema 1 | 1.362343 |
| Desviación estándar-Sistema 2 | 2.887603 |
| Tamaño del Sistema 1 | 25 |
| Tamaño del Sistema 2 | 30 |
| Hipótesis Alternativa Diferente de | 1 |
| Intervalos de Confianza para el cociente de Varianzas | 95% |
| Límite Inferior | 0.1033358 |
| Límite Superior | 0.4935717 |
Intervalo de Confianza para Desviación Estándar
| Límite Inferior | Desviación Estádar | Límite Superior | |
|---|---|---|---|
| Sistema 1 | 1.064 | 1.362 | 1.895 |
| Sistema 2 | 2.300 | 2.888 | 3.882 |
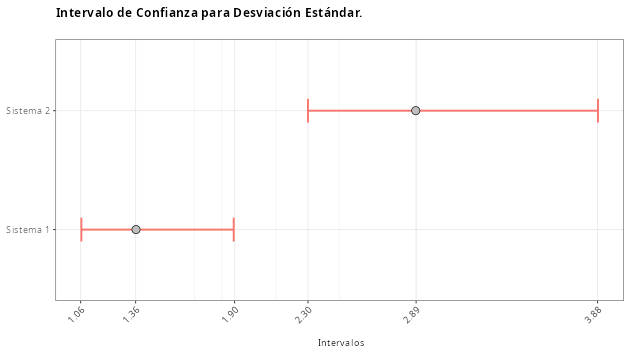
Al realizar la prueba F para dos varianzas, observamos que el valor p es 0,0003578, o menos del 5 %. Por lo tanto, rechazamos la hipótesis de que las varianzas sean iguales.
Ejemplo 2:
Un analista de calidad desea evaluar si existen diferencias en las medidas de los ejes de comando desarrolladas por dos sistemas de mecanizado. Los valores de las desviaciones estándar son 1.362346 y 2.887603 y los tamaños de las muestras son 25 y 20. ¿Con un nivel de confianza del 95%, existe una diferencia significativa entre la variabilidad de las medidas de los ejes de mando de los dos sistemas de mecanizado?
Para realizar una prueba de dos varianzas, se realiza la siguiente configuración como se muestra en la siguiente figura.
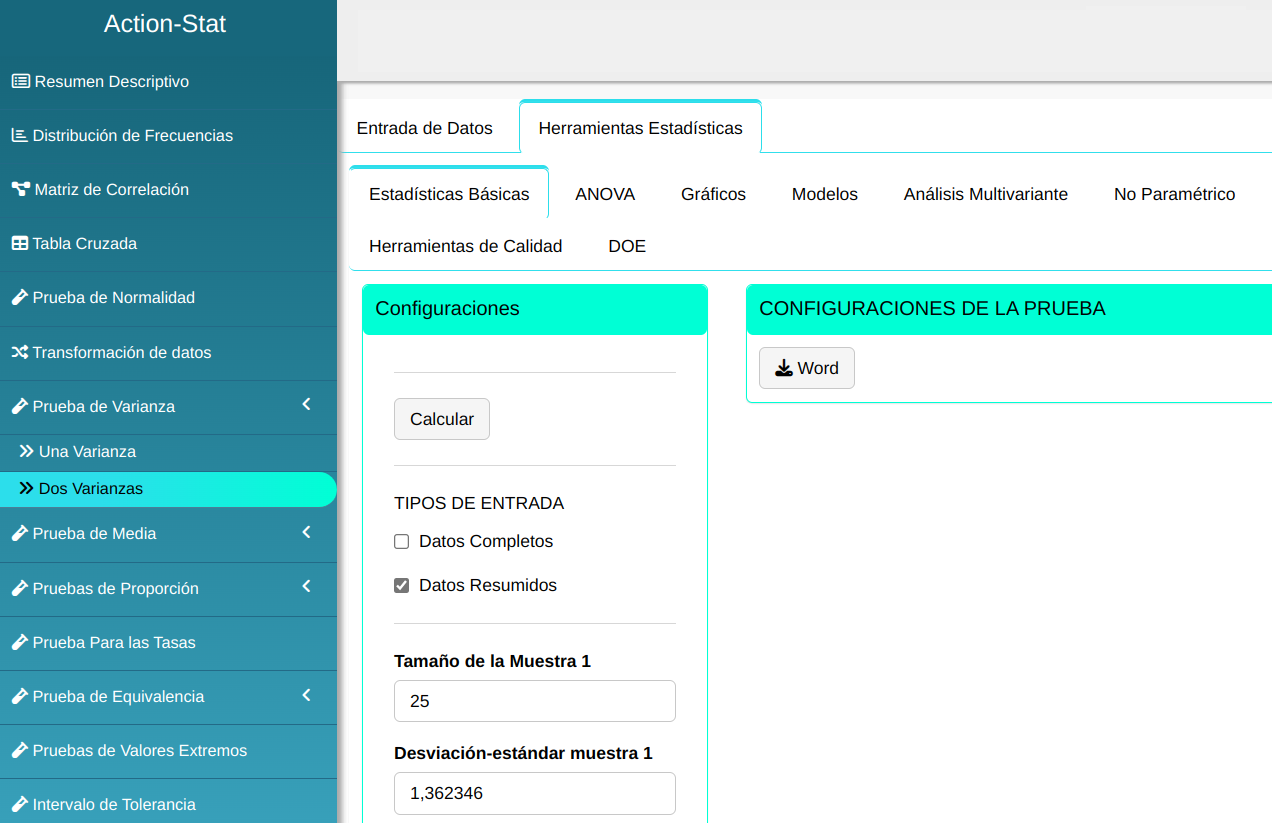
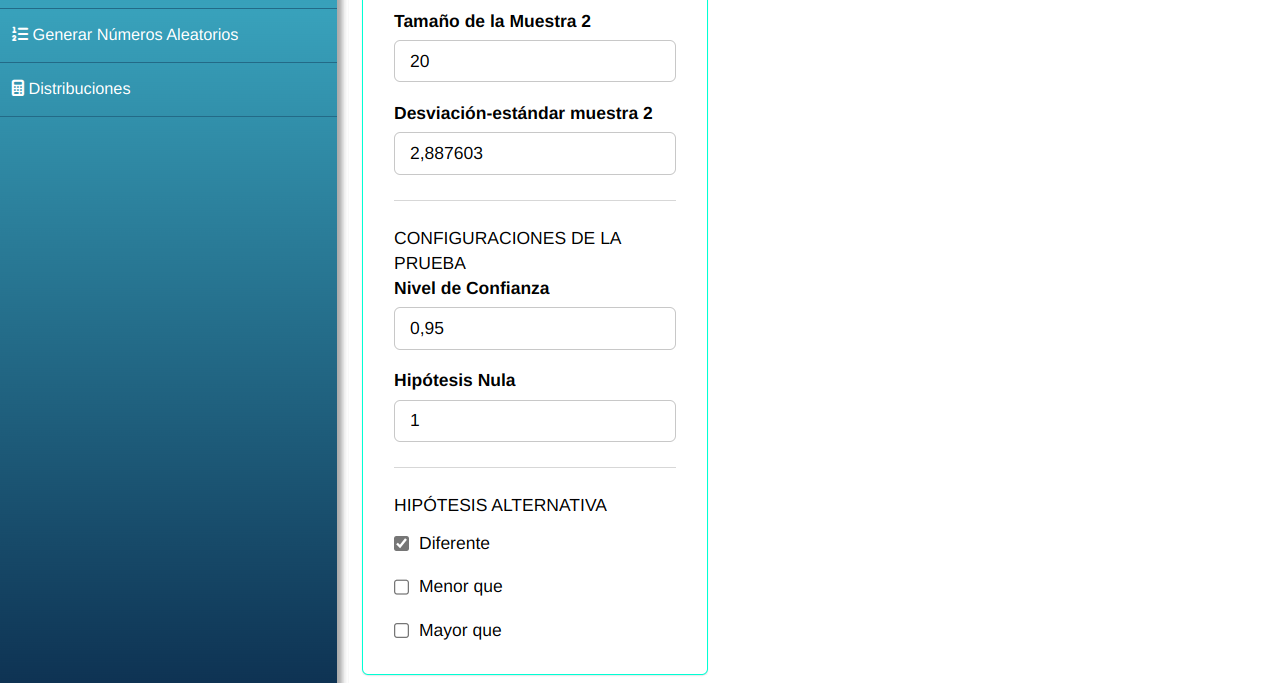
Clicando en Calcular obtenemos los resultados. También se puede generar y descargar los resultados en un archivo Word.

Los resultados son:
Prueba de dos varianzas
| Valores | |
|---|---|
| Estadística F | 0.222587 |
| Grados de libertad (Numerador) | 24 |
| Grados de libertad (Denominador) | 19 |
| P-Valor | 0.000716142 |
| Desviación Estándar - Muestra 1 | 1.362346 |
| Desviación Estándar - Muestra 2 | 2.887603 |
| Tamaño de la Mustra | 25 |
| Tamaño de la Muestra | 20 |
| Hipótesis Alternativa Diferente | 1 |
| Intervalo de Confianza para la razón de varianza | 95% |
| Límite Inferior | 0.09076587 |
| Límite Superior | 0.493574 |
Intervalo de Confianza para Desviación estándar
| Límite Inferior | Desviación Estádar | Límite Superior | |
|---|---|---|---|
| muestra 1 | 1.0638 | 1.3623 | 1.8952 |
| muestra 2 | 2.196 | 2.8876 | 4.2176 |
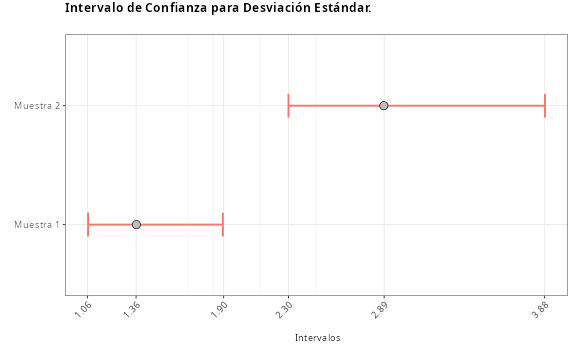
Ejecutando la prueba F - Dos varianzas, vemos que el P-valor es 0.000716142, es decir, es menor al 5%. Por lo tanto, rechazamos la hipótesis nula de que las varianzas son iguales.