1. ID Plot
La herramienta ID Plot de Action permite determinar qué distribución describe mejor la aleatoriedad de um conjunto de datos: Normal, Log-Normal, Exponencial, Logística, Gamma, Weibull y Gumbel. Esta herramienta permite elegir entre los gráficos QQ-Plot, Histograma y Función de densidad, así como las pruebas de hipótesis de Anderson-Darling, Cramer-von-Misses y Kolmogorov-Smirnov.
Ejemplo:
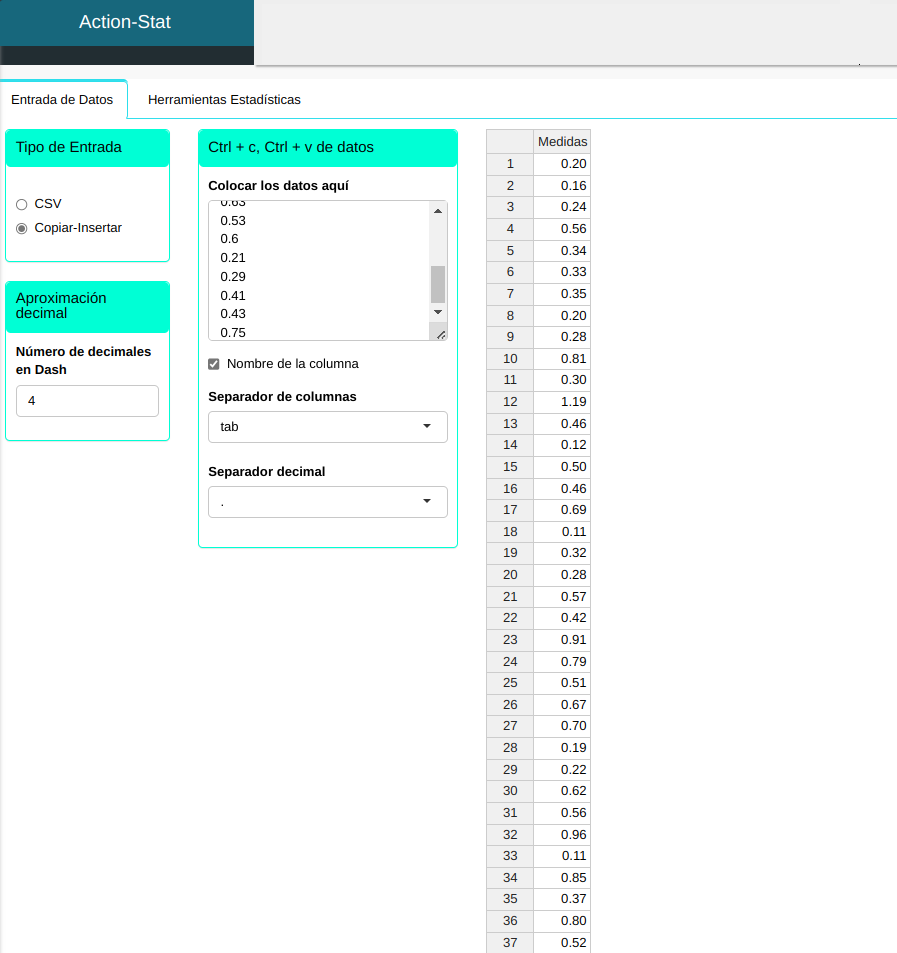
Consideremos el conjunto de datos de la tabla siguiente. Veamos qué distribución de probabilidad describe mejor este conjunto de datos.
| Medidas |
|---|
| 0.20 |
| 0.16 |
| 0.24 |
| 0.56 |
| 0.34 |
| 0.33 |
| 0.35 |
| 0.20 |
| 0.28 |
| 0.81 |
| 0.30 |
| 1.19 |
| 0.46 |
| 0.12 |
| 0.50 |
| 0.46 |
| 0.69 |
| 0.11 |
| 0.32 |
| 0.28 |
| 0.57 |
| 0.42 |
| 0.91 |
| 0.79 |
| 0.51 |
| 0.67 |
| 0.70 |
| 0.19 |
| 0.22 |
| 0.62 |
| 0.56 |
| 0.96 |
| 0.11 |
| 0.85 |
| 0.37 |
| 0.80 |
| 0.52 |
| 0.17 |
| 0.58 |
| 0.15 |
| 0.20 |
| 0.05 |
| 0.63 |
| 0.53 |
| 0.60 |
| 0.21 |
| 0.29 |
| 0.41 |
| 0.43 |
| 0.75 |
Hacemos el upload de los datos en el sistema.
Realizaremos el análisis, y configuramos conforme la figura abajo.
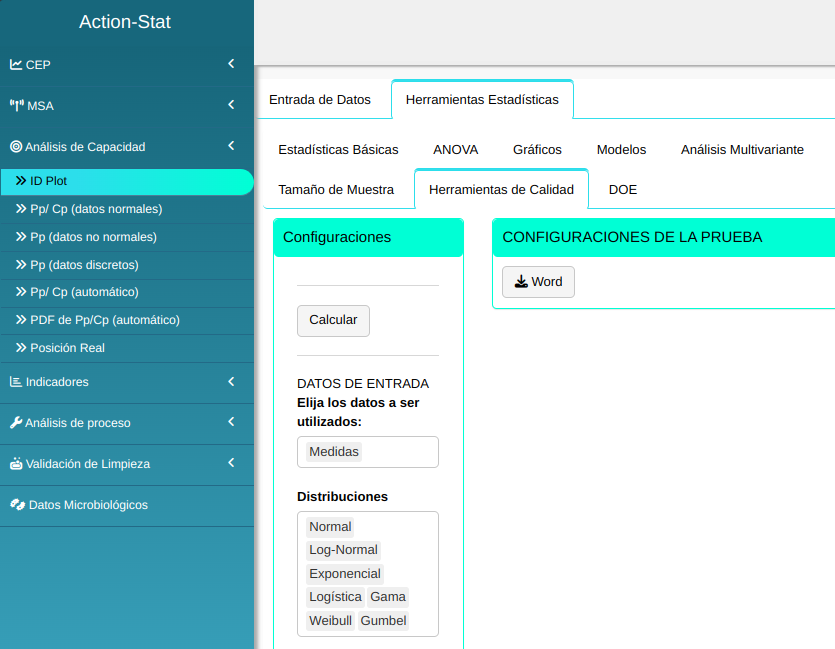
En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.
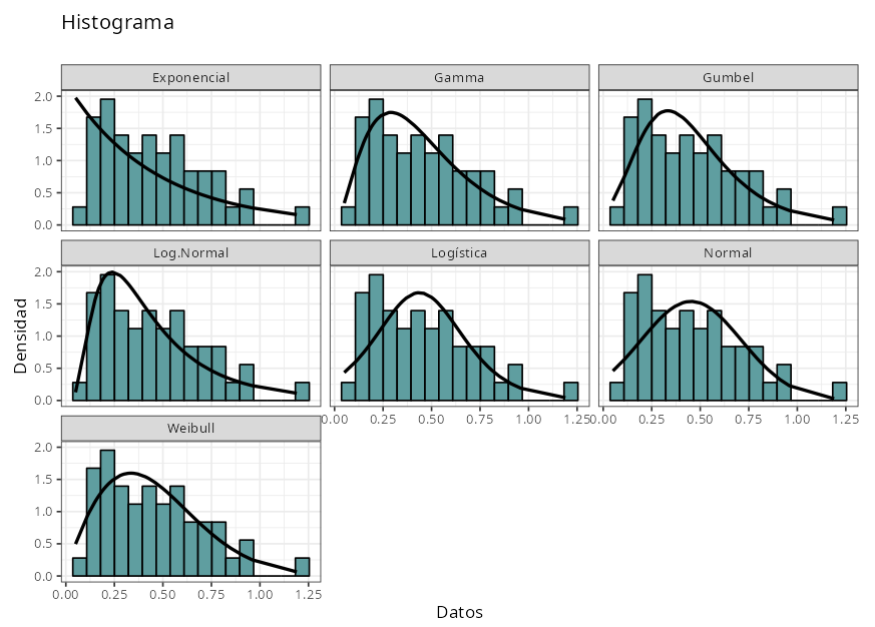
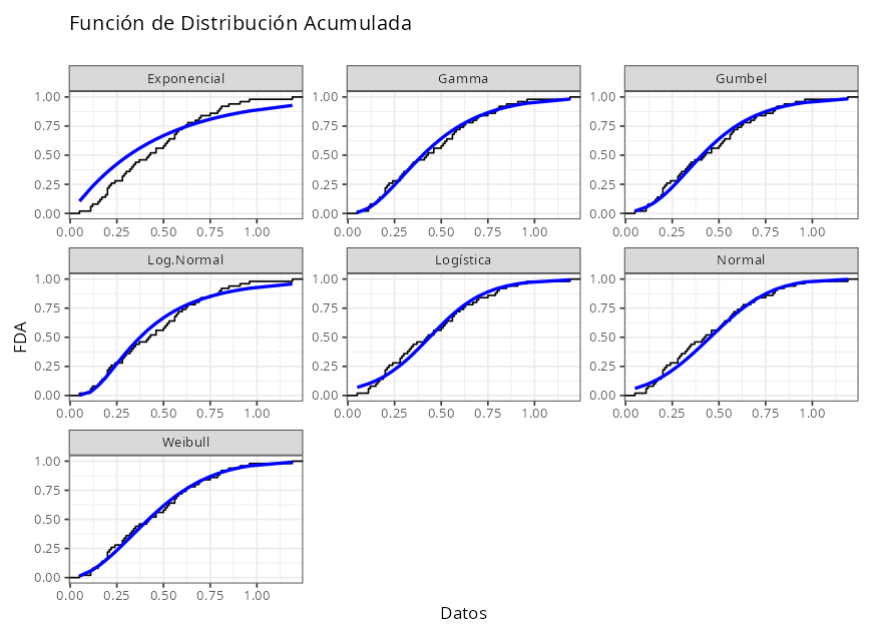
Los resultados son:
Resultado del análisis
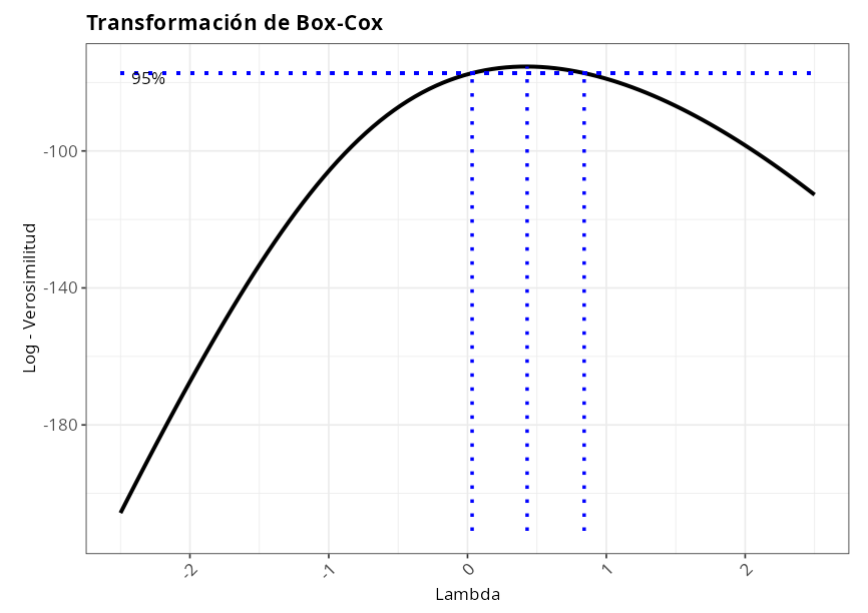
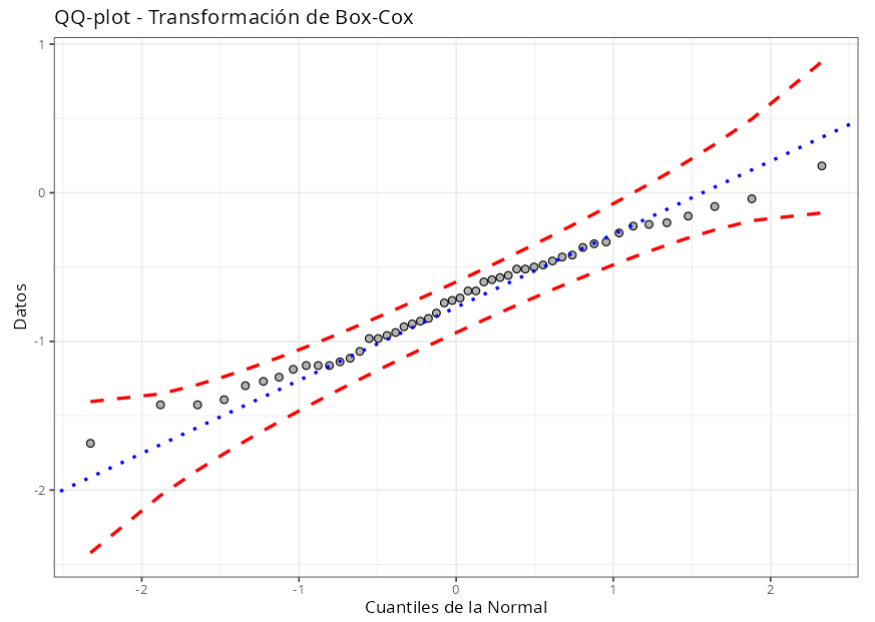
| Transformación de Box-Cox | ||
Resultados
| Valores | |
|---|---|
| Lambda | 0.429 |
| P-Valor (Anderson-Darling) | 0.703 |
Resultado del análisis
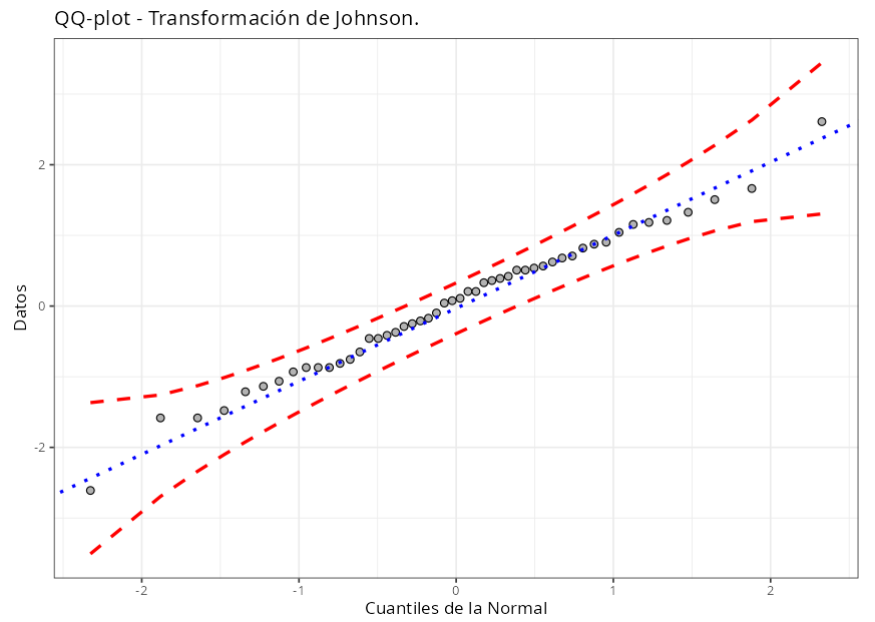
| Transformación de Johnson | ||
Estimativas
| Prueba | |
|---|---|
| Gamma | 0.90802942754439 |
| Lambda | 1.36936290670753 |
| Epsilon | 0.0168457063069285 |
| Eta | 0.951739827664239 |
| Família | SB |
| P-Valor (Anderson-Darling) | 0.9422 |
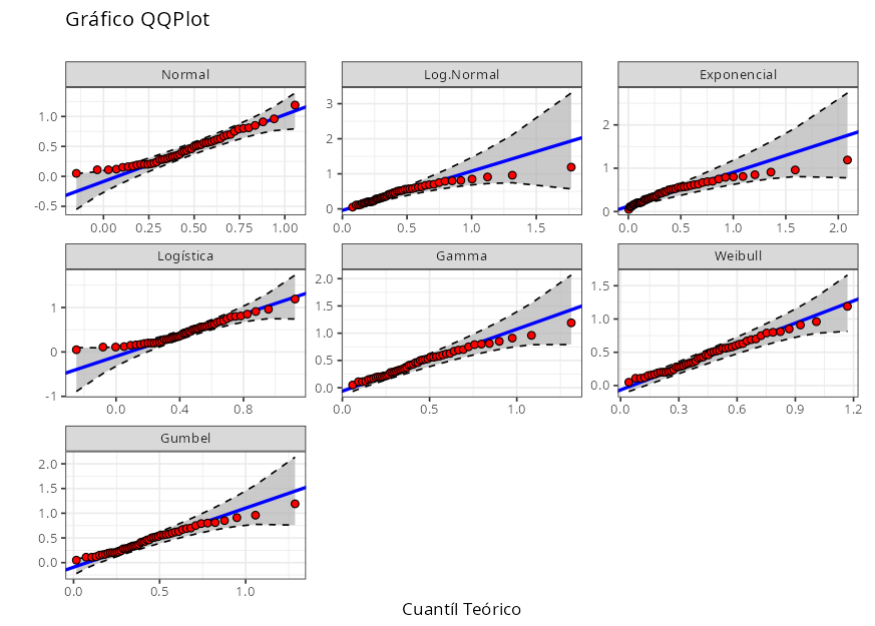
Anderson-Darling
| Distribuciones | Estadística | P-Valor | |
|---|---|---|---|
| 1 | Normal($\mu$ = 0.45, $\sigma$ = 0.26) | 0.566 | 0.136 |
| 2 | Log-Normal(log($\mu$) = -0.982398, log($\sigma$)= 0.667801) | 0.589 | 0.118 |
| 1-mle-exp | Exponencial(Tasa = 2.20556) | 3.845 | 0.000 |
| 11 | Logística(Posición = 0.44, Escala = 0.15) | 0.581 | 0.089 |
| 12 | Gamma(Forma = 2.76743, Tasa = 6.10372) | 0.295 | 0.250 |
| 13 | Weibull(Forma = 1.84755, Escala = 0.511436) 0.217 | 0.250 | |
| 14 | Gumbel(Posición = 0.332819, Escala = 0.207431) | 0.384 | 0.250 |
Cramer-von-Misés
| Distribuciones | Estadística | P-Valor |
|---|---|---|
| Normal($\mu$ = 0.45, $\sigma$ = 0.26) | 0.082 | 0.192 |
| Log-Normal(log($\mu$) = -0.982398, log($\sigma$) = 0.667801) | 0.100 | 0.114 |
| Exponencial(Tasa = 2.20556) | 0.678 | 0.000 |
| Logística(Posición = 0.44, Escala = 0.15) | 0.076 | 0.232 |
| Gamma(Forma = 2.76743, Tasa = 6.10372) | 0.051 | 0.497 |
| Weibull(Forma = 1.84755, Escala = 0.511436) | 0.035 | 0.765 |
| Gumbel(Posición = 0.332819, Escala = 0.207431) | 0.065 | 0.329 |
Kolmogorov-Smirnov
| Distribuciones | Estadística | P-Valor |
|---|---|---|
| Normal($\mu$ = 0.45, $\sigma$ = 0.26) | 0.095 | 0.313 |
| Log-Normal(log($\mu$) = -0.982398, log($\sigma$) = 0.667801) | 0.108 | 0.158 |
| Exponencial(Tasa = 2.20556) | 0.202 | 0.000 |
| Logística(Posición = 0.44, Escala = 0.15) | 0.082 | 0.550 |
| Gamma(Forma = 2.76743, Tasa = 6.10372) | 0.083 | 0.534 |
| Weibull(Forma = 1.84755, Escala = 0.511436) | 0.070 | 0.778 |
| Gumbel(Posición = 0.332819, Escala = 0.207431) | 0.081 | 0.559 |
Resultados del Análisis
| Análisis Gráfico | ||