3. Indices de Rendimiento - Pp (Datos no Normales)
En varias situaciones estamos interesados en evaluar el desempeño de un proceso de producción sobre una característica determinada. Sin embargo, es posible que la distribución normal no se ajuste bien a los datos. En esta situación, podemos encontrar una distribución de probabilidad alternativa o utilizar un método no paramétrico.
Ejemplo 1:
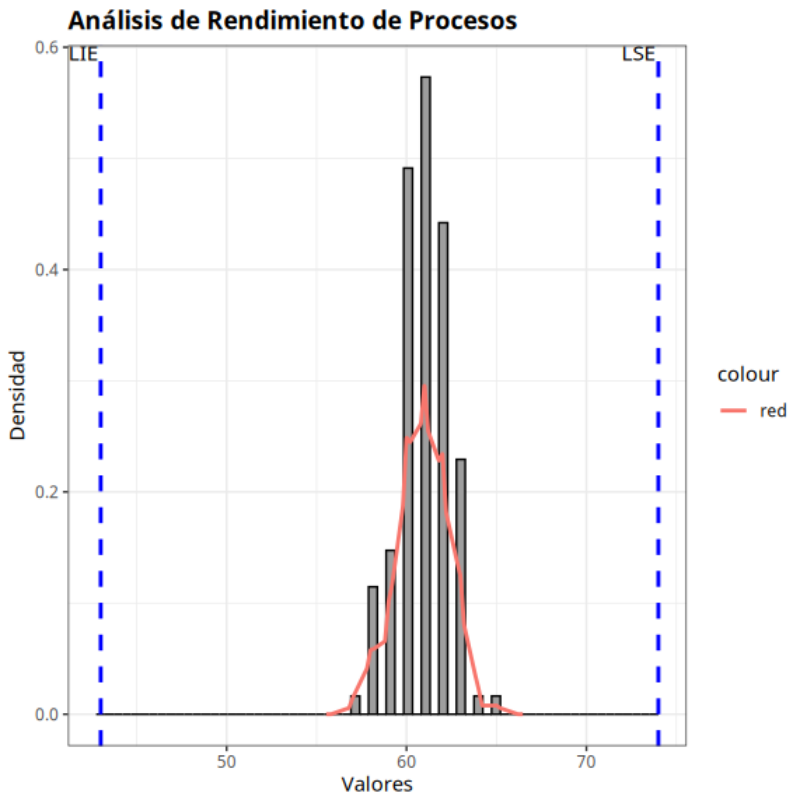
Consideremos los datos de la siguiente tabla referentes a las medidas del diámetro de un cilindro número 3, elaborado rápidamente y tomando 5 piezas por cada 20 producidas. Las especificaciones para estos datos son: LSE = 74 y LIE = 43.
| Fecha | Hora | Lámina | M1 | M2 | M3 | M4 | M5 |
|---|---|---|---|---|---|---|---|
| 26/abr | 11:40 | 14650 | 61 | 62 | 60 | 61 | 60 |
| 26/abr | 13:10 | 14650 | 62 | 61 | 62 | 63 | 62 |
| 26/abr | 17:15 | 19730 | 61 | 58 | 61 | 60 | 60 |
| 26/abr | 21:35 | 19730 | 62 | 60 | 62 | 61 | 60 |
| 28/abr | 7:08 | 14650 | 63 | 62 | 61 | 60 | 62 |
| 28/abr | 8:15 | 14650 | 62 | 61 | 58 | 59 | 60 |
| 28/abr | 10:03 | 14650 | 62 | 61 | 60 | 62 | 61 |
| 28/abr | 12:44 | 14650 | 62 | 61 | 60 | 58 | 59 |
| 28/abr | 14:12 | 14650 | 62 | 61 | 60 | 60 | 61 |
| 28/abr | 17:20 | 19730 | 61 | 60 | 60 | 61 | 63 |
| 28/abr | 19:20 | 19730 | 59 | 61 | 60 | 59 | 61 |
| 28/abr | 22:30 | 19730 | 61 | 60 | 62 | 62 | 60 |
| 29/abr | 7:28 | 14650 | 62 | 61 | 60 | 58 | 57 |
| 29/abr | 8:40 | 14650 | 61 | 60 | 59 | 58 | 58 |
| 29/abr | 11:36 | 14650 | 62 | 61 | 60 | 61 | 61 |
| 29/abr | 12:50 | 14650 | 61 | 60 | 62 | 61 | 62 |
| 29/abr | 14:18 | 14650 | 62 | 61 | 63 | 62 | 63 |
| 29/abr | 18:15 | 19730 | 61 | 63 | 63 | 62 | 61 |
| 29/abr | 22:45 | 19730 | 60 | 59 | 60 | 61 | 60 |
| 30/abr | 10:01 | 14650 | 63 | 62 | 61 | 60 | 62 |
| 30/abr | 12:20 | 14650 | 61 | 60 | 59 | 58 | 59 |
| 30/abr | 16:50 | 19730 | 63 | 61 | 63 | 62 | 61 |
| 30/abr | 18:15 | 19730 | 61 | 60 | 60 | 59 | 60 |
| 30/abr | 21:35 | 19730 | 63 | 65 | 63 | 64 | 63 |
| 5/mayo | 12:58 | 14650 | 61 | 62 | 63 | 62 | 60 |
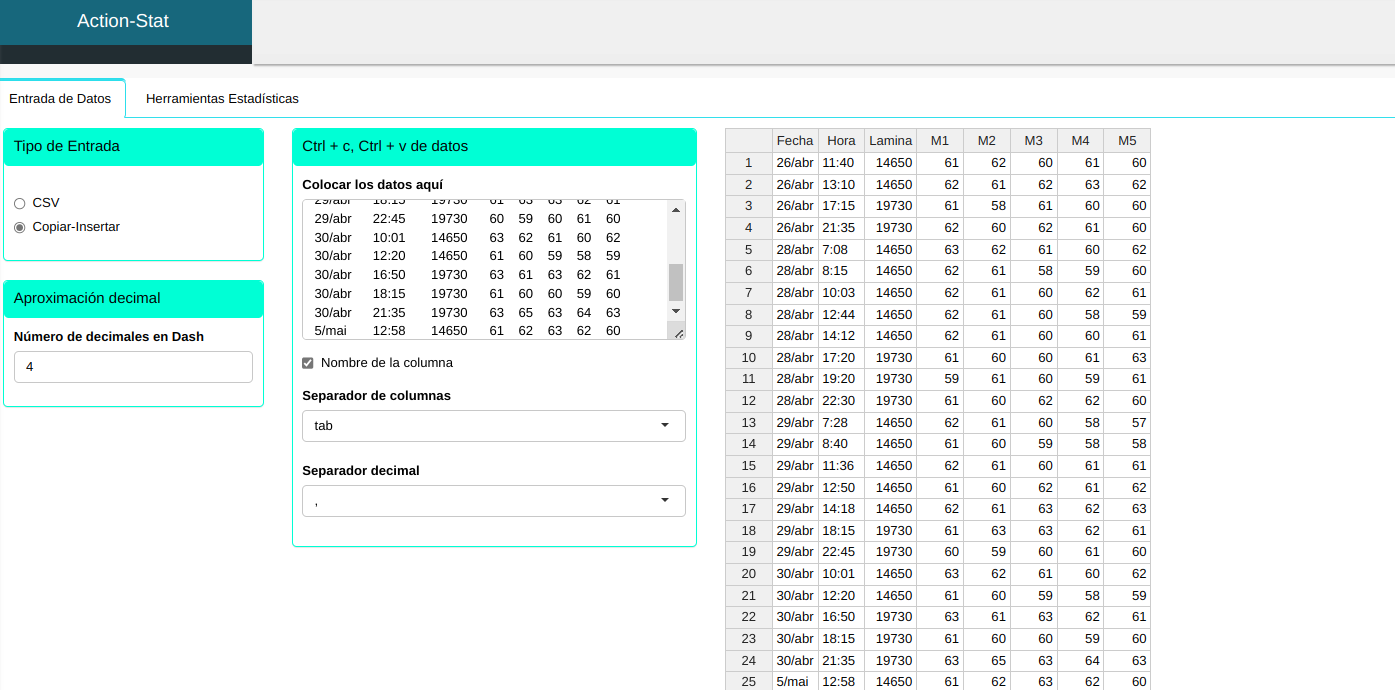
Subiremos los datos al sistema.
Realizaremos el análisis, y configuramos conforme la figura abajo.
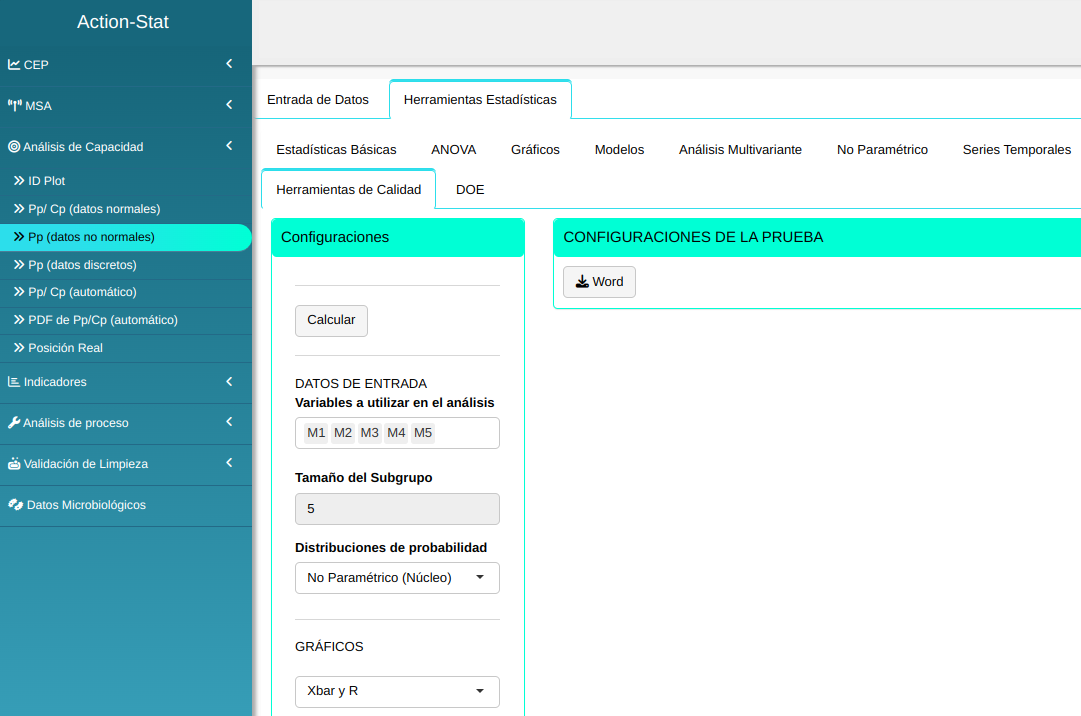
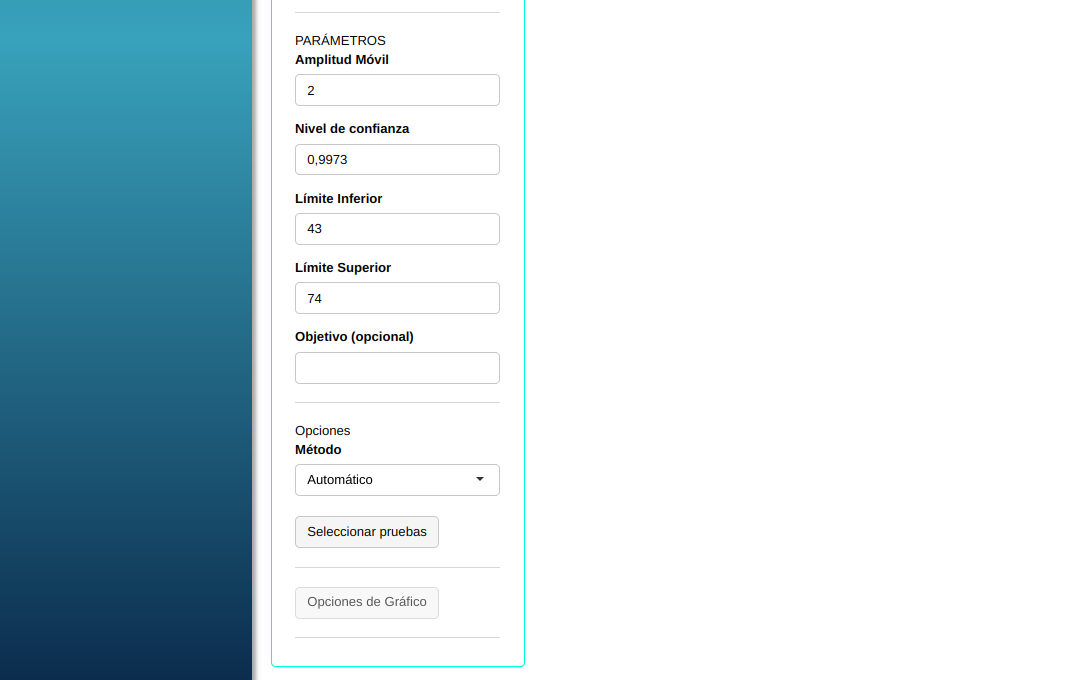
- En “Seleccionar pruebas” podemos elegir las pruebas que queremos realizar.
En seguida, haga un clic en calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.
Los resultados son:
Especificaciones
| Valor | |
|---|---|
| Muestra: | 125 |
| Límite inferior | 43 |
| Límite superior | 74 |
Estimativas
| Parámetros | Valor |
|---|---|
| Media: | 60.912 |
| Desviación estándar: | 1.42566339962568 |
Índices de Desempeño
| Índices de desempeño | |
|---|---|
| PP | 3.4431 |
| PPI | 4.0347 |
| PPS | 2.8655 |
| PPk | 2.8655 |
Índices observados
| Índices observados | |
|---|---|
| PPM > LSE | 0 |
| PPM < LIE | 0 |
| PPM total | 0 |
Índices esperados
| Índices esperados | |
|---|---|
| PPM > LSE | 0 |
| PPM < LIE | 0 |
| PPM total | 0 |
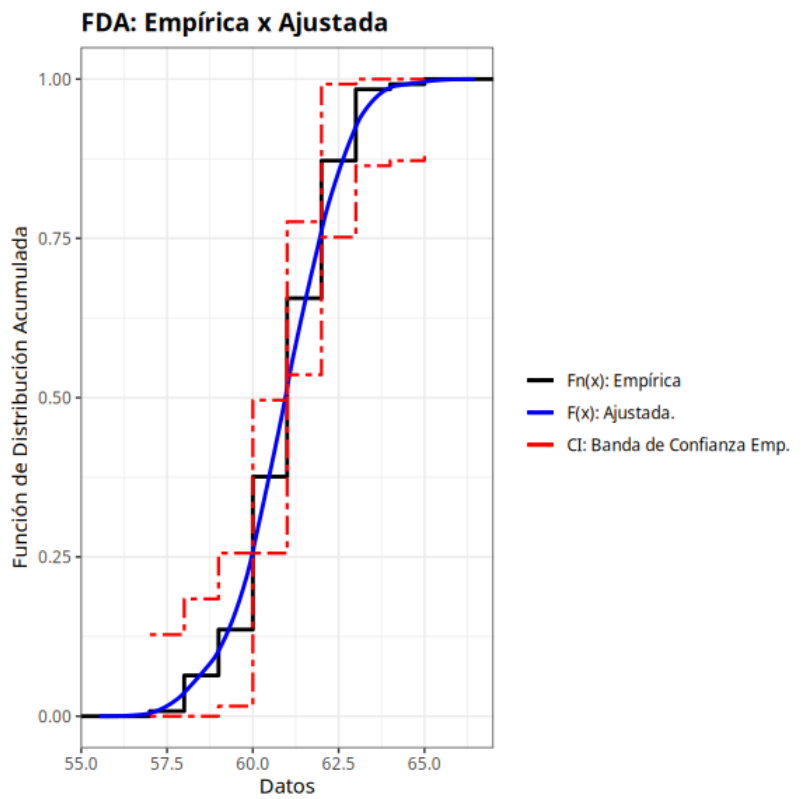
Calidad de ajuste (No Paramétrico (Núcleo): Método triangular)
| Método | Estadística $X^2$ | P-valor | |
|---|---|---|---|
| Cramer-von Mises | triangular | 1.089 | 0.219 |
| Kolmogorov-Smirnov | triangular | 0.144 | 0.150 |
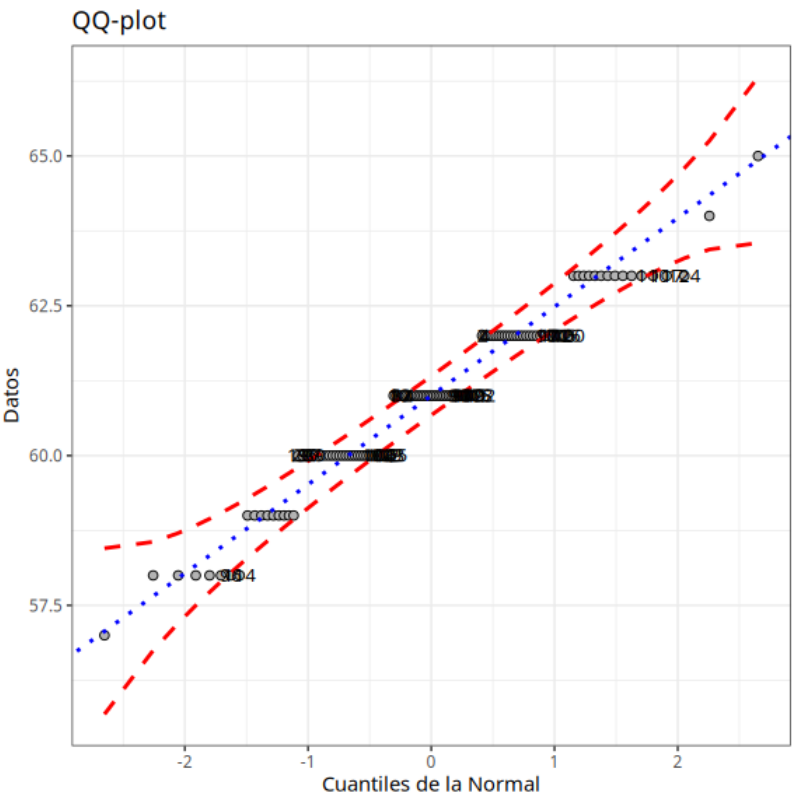
Prueba de Normalidad (valores atípicos)
| Obs. | Cuantiles de la Normal | Datos | Criterio |
|---|---|---|---|
| 19 | -1.08 | 60 | Banda de confianza (Nivel de confianza=95%) |
| 29 | -1.05 | 60 | Banda de confianza (Nivel de confianza=95%) |
| 35 | -1.01 | 60 | Banda de confianza (Nivel de confianza=95%) |
| 37 | -0.98 | 60 | Banda de confianza (Nivel de confianza=95%) |
| 39 | -0.95 | 60 | Banda de confianza (Nivel de confianza=95%) |
| 1 | -0.31 | 61 | Banda de confianza (Nivel de confianza=95%) |
| 3 | -0.28 | 61 | Banda de confianza (Nivel de confianza=95%) |
| 10 | -0.26 | 61 | Banda de confianza (Nivel de confianza=95%) |
| 12 | -0.24 | 61 | Banda de confianza (Nivel de confianza=95%) |
| 14 | -0.22 | 61 | Banda de confianza (Nivel de confianza=95%) |
| 2 | 0.41 | 62 | Banda de confianza (Nivel de confianza=95%) |
| 4 | 0.43 | 62 | Banda de confianza (Nivel de confianza=95%) |
| 96 | -1.63 | 58 | Banda de confianza (Nivel de confianza=95%) |
| 114 | -1.55 | 58 | Banda de confianza (Nivel de confianza=95%) |
| 104 | -0.43 | 60 | Banda de confianza (Nivel de confianza=95%) |
| 106 | -0.41 | 60 | Banda de confianza (Nivel de confianza=95%) |
| 112 | -0.39 | 60 | Banda de confianza (Nivel de confianza=95%) |
| 119 | -0.37 | 60 | Banda de confianza (Nivel de confianza=95%) |
| 123 | -0.35 | 60 | Banda de confianza (Nivel de confianza=95%) |
| 125 | -0.33 | 60 | Banda de confianza (Nivel de confianza=95%) |
| 90 | 0.22 | 61 | Banda de confianza (Nivel de confianza=95%) |
| 91 | 0.24 | 61 | Banda de confianza (Nivel de confianza=95%) |
| 94 | 0.26 | 61 | Banda de confianza (Nivel de confianza=95%) |
| 107 | 0.28 | 61 | Banda de confianza (Nivel de confianza=95%) |
| 109 | 0.31 | 61 | Banda de confianza (Nivel de confianza=95%) |
| 111 | 0.33 | 61 | Banda de confianza (Nivel de confianza=95%) |
| 115 | 0.35 | 61 | Banda de confianza (Nivel de confianza=95%) |
| 118 | 0.37 | 61 | Banda de confianza (Nivel de confianza=95%) |
| 122 | 0.39 | 61 | Banda de confianza (Nivel de confianza=95%) |
| 97 | 0.95 | 62 | Banda de confianza (Nivel de confianza=95%) |
| 100 | 0.98 | 62 | Banda de confianza (Nivel de confianza=95%) |
| 102 | 1.01 | 62 | Banda de confianza (Nivel de confianza=95%) |
| 105 | 1.05 | 62 | Banda de confianza (Nivel de confianza=95%) |
| 116 | 1.08 | 62 | Banda de confianza (Nivel de confianza=95%) |
| 120 | 1.12 | 62 | Banda de confianza (Nivel de confianza=95%) |
| 110 | 1.8 | 63 | Banda de confianza (Nivel de confianza=95%) |
| 117 | 1.91 | 63 | Banda de confianza (Nivel de confianza=95%) |
| 124 | 2.05 | 63 | Banda de confianza (Nivel de confianza=95%) |
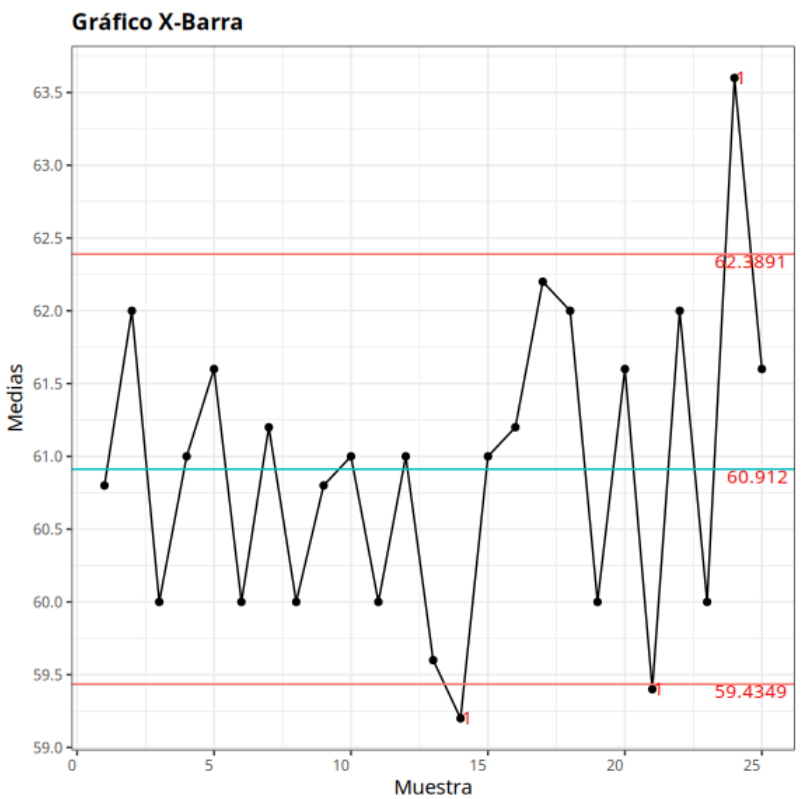
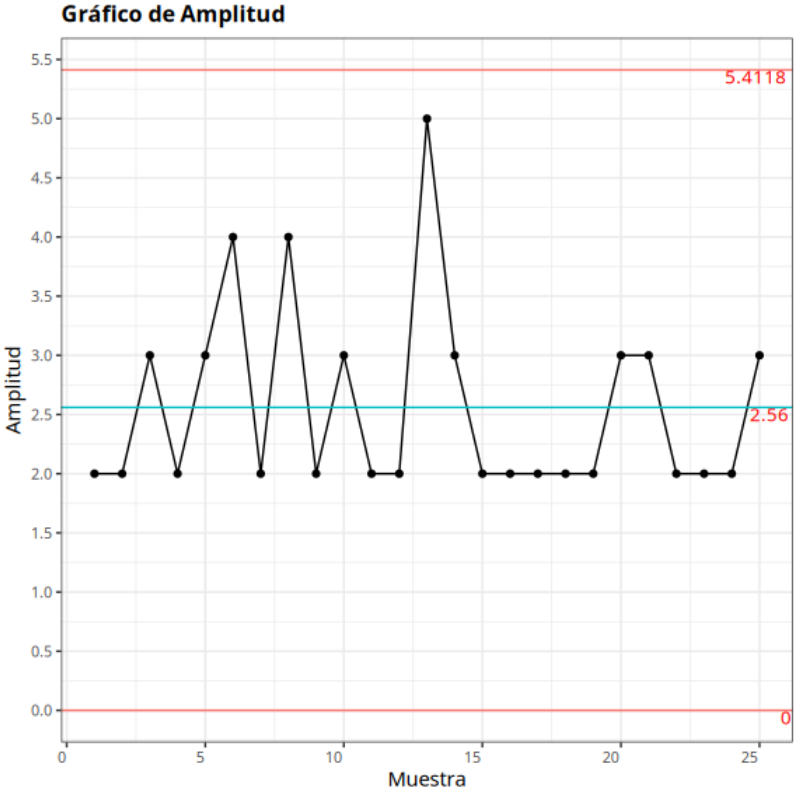
Puntos fuera de control - Gráfico X-Barra
| Subgrupo | Valor | Prueba |
|---|---|---|
| 14 | 59.2 | 1 punto a más de 3 Sigmas de la línea central |
| 21 | 59.4 | 1 punto a más de 3 Sigmas de la línea central |
| 24 | 63.6 | 1 punto a más de 3 Sigmas de la línea central |
Ejemplo 2:
Los datos utilizados en este ejemplo se refieren al gramaje (g/$m^2$) de una hoja de papel. Las especificaciones de estos datos son LSE = 92.88; Objetivo = 90.21 y LIE = 87.54.
| Gramaje g/m2 |
|---|
| 88.20 |
| 88.90 |
| 90.50 |
| 90.30 |
| 90.00 |
| 90.20 |
| 91.20 |
| 91.00 |
| 91.50 |
| 91.40 |
| 91.30 |
| 90.20 |
| 91.40 |
| 89.90 |
| 90.20 |
| 90.10 |
| 90.80 |
| 91.40 |
| 91.30 |
| 89.00 |
| 90.70 |
| 89.50 |
| 91.20 |
| 90.50 |
| 90.60 |
Subiremos los datos al sistema.
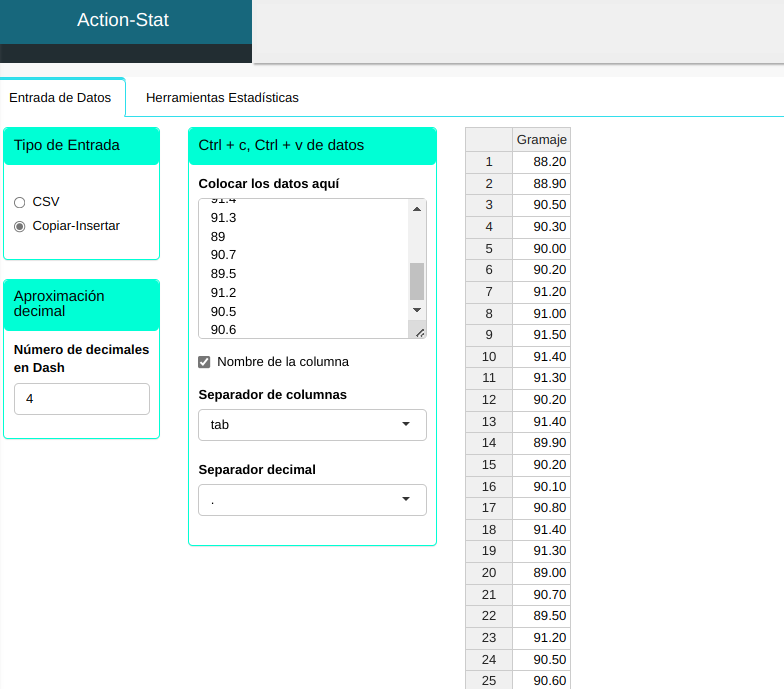
Haremos el análisis ajustando conforme la figura de abajo.
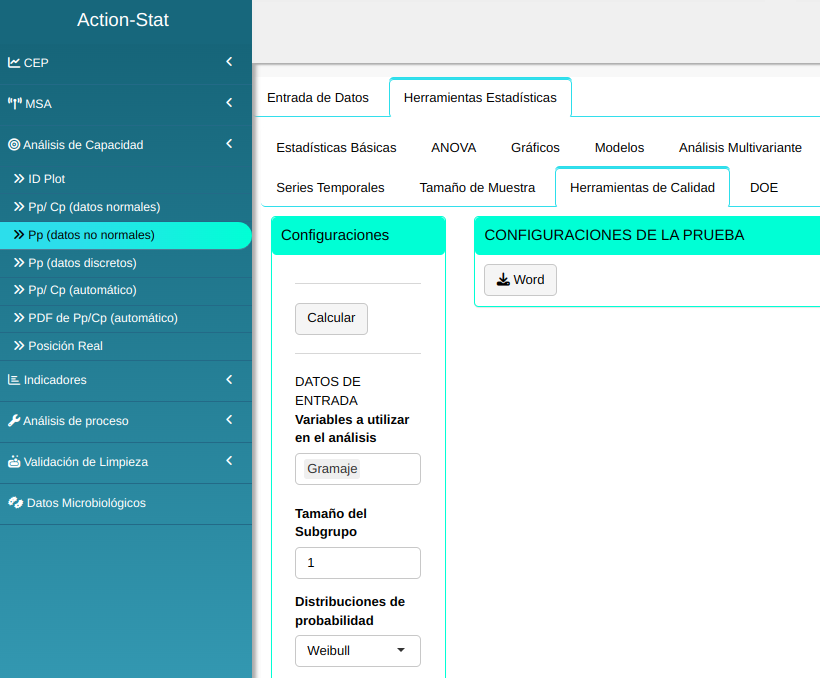
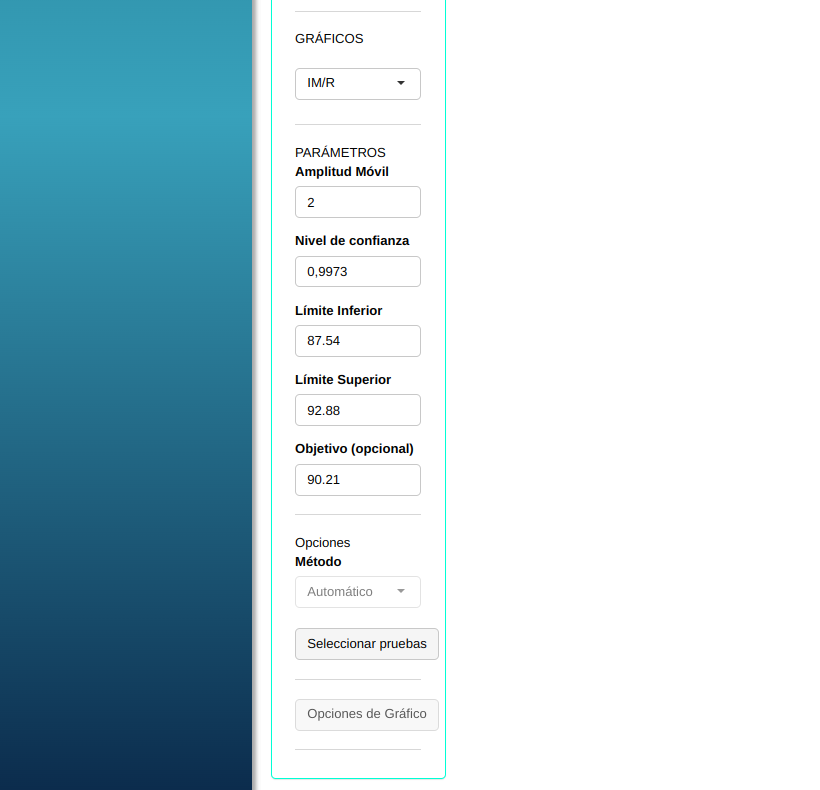
- En “seleccionar pruebas” podemos elegir las pruebas que queremos realizar
Clicando em Calcular obtemos os resultados e também é possível gerar a análise e baixar em formato Word.
Los resultados son:
Especificaciones
| Valor | |
|---|---|
| Muestra: | 25 |
| Límite inferior | 87.54 |
| Objetivo (opcional) | 90.21 |
| Límite superior | 92.88 |
Estimaciones
| Parámetros | Valor |
|---|---|
| Promedio: | 90.4689587801872 |
| Desviación estándar: | 0.822555917720036 |
| Forma: | 140.336103078599 |
| Escala: | 90.8380519338829 |
Índices de desempeño
| Índices de desempeño | |
|---|---|
| PP | 0.987 |
| IPP | 0.777 |
| PPP | 1.553 |
| PPk | 0.777 |
Índices observados
| Índices observados | |
|---|---|
| PPM > LSE | 0 |
| PPM < LIE | 0 |
| PPM totales | 0 |
Índices Esperados
| Índices Esperados | |
|---|---|
| PPM > LSE | 0.000147211465240105 |
| PPM < LIE | 5556.66966289269 |
| PPM Total | 5556.66981010415 |
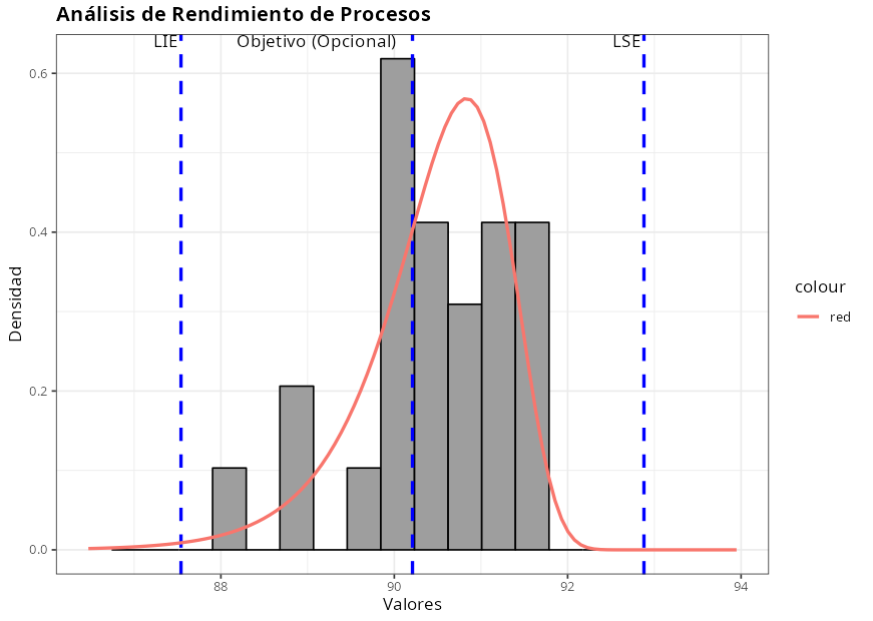
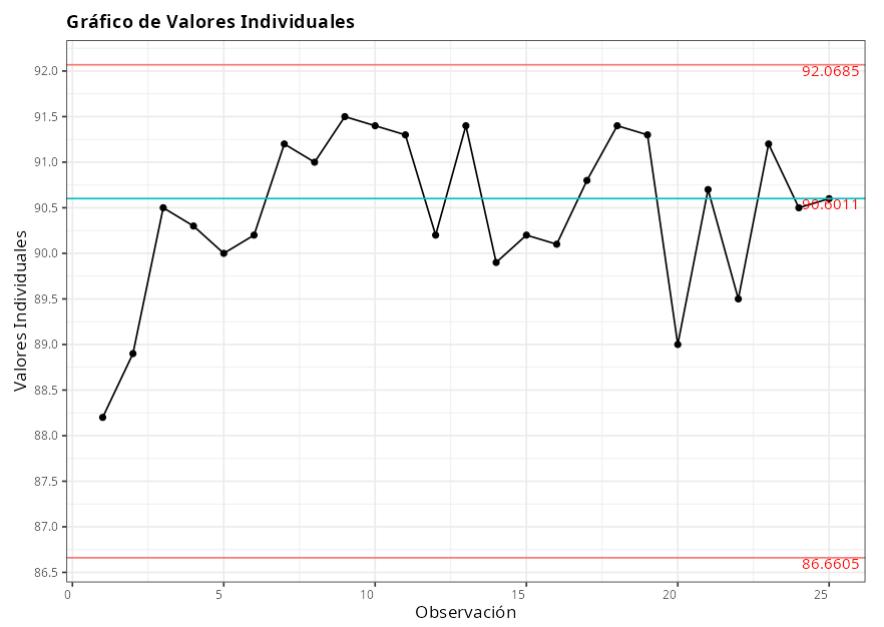
Ejemplo 3:
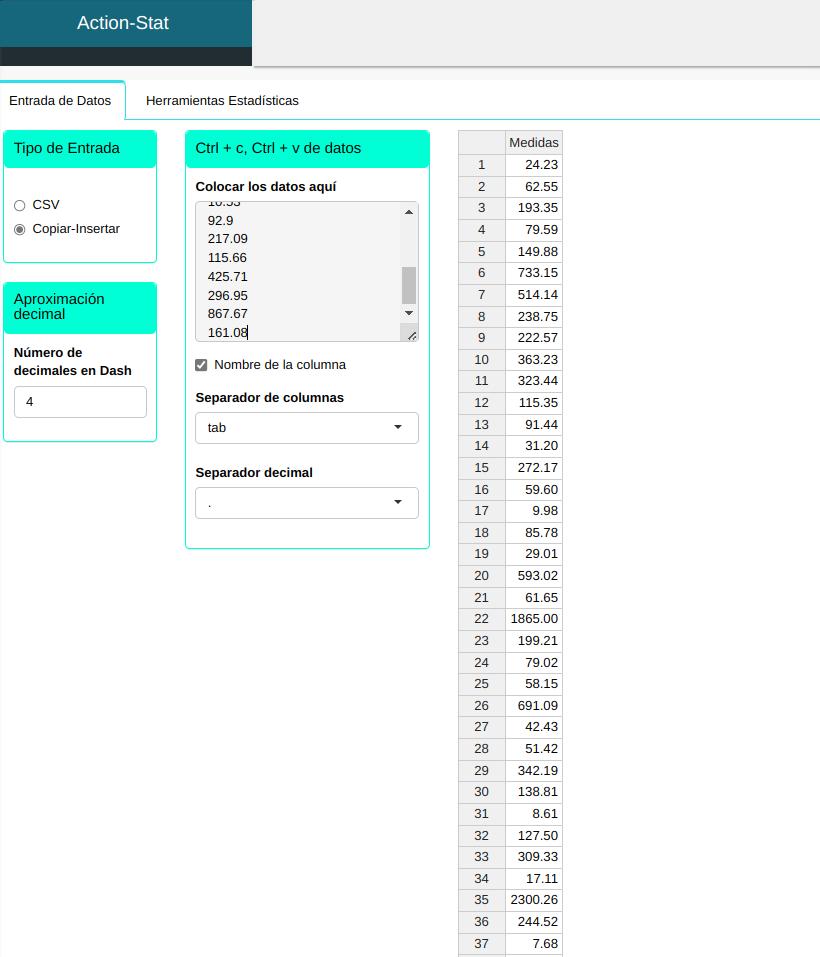
Consideremos los datos sobre las medidas, que se muestran en la siguiente tabla. Las especificaciones para estos datos son LSE = 3000 y LIE = 30.
| Medidas |
|---|
| 24.23 |
| 62.55 |
| 193.35 |
| 79.59 |
| 149.88 |
| 733.15 |
| 514.14 |
| 238.75 |
| 222.57 |
| 363.23 |
| 323.44 |
| 115.35 |
| 91.44 |
| 31.2 |
| 272.17 |
| 59.6 |
| 9.98 |
| 85.78 |
| 29.01 |
| 593.02 |
| 61.65 |
| 1865 |
| 199.21 |
| 79.02 |
| 58.15 |
| 691.09 |
| 42.43 |
| 51.42 |
| 342.19 |
| 138.81 |
| 8.61 |
| 127.5 |
| 309.33 |
| 17.11 |
| 2300.26 |
| 244.52 |
| 7.68 |
| 83.97 |
| 45.33 |
| 520.4 |
| 3556.16 |
| 59.75 |
| 10.53 |
| 92.9 |
| 217.09 |
| 115.66 |
| 425.71 |
| 296.95 |
| 867.67 |
| 161.08 |
Subiremos los datos al sistema.
Realizaremos el análisis ajustando conforme la figura abajo.
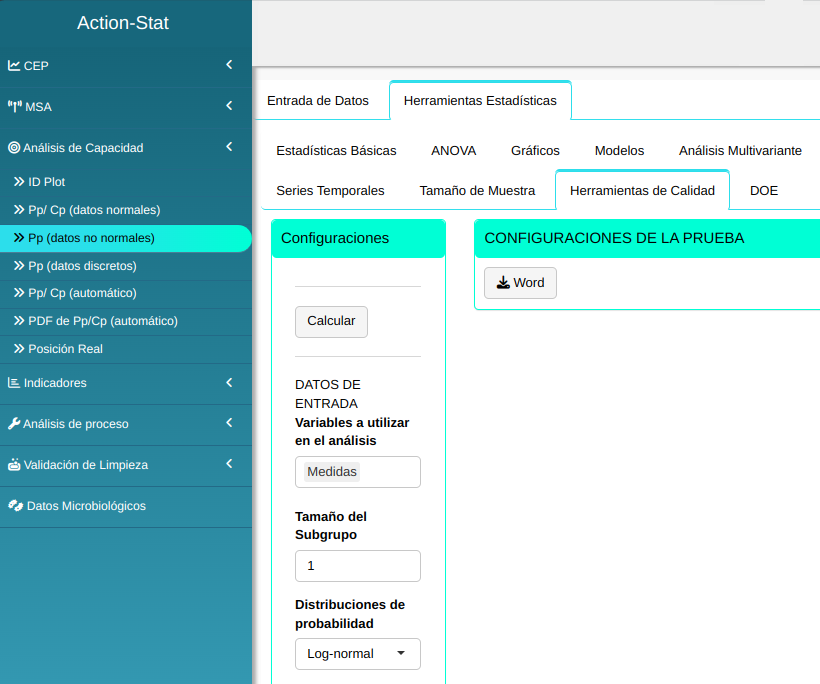
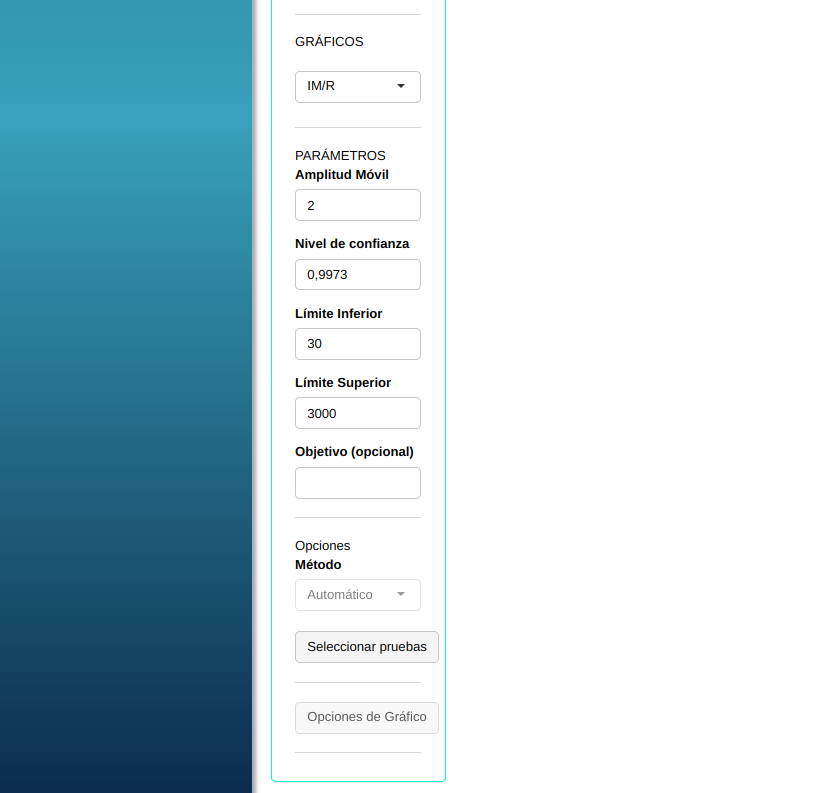
- En “seleccionar pruebas” podemos elegir las pruebas que queremos realizar
En seguida, haga un clic en calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.
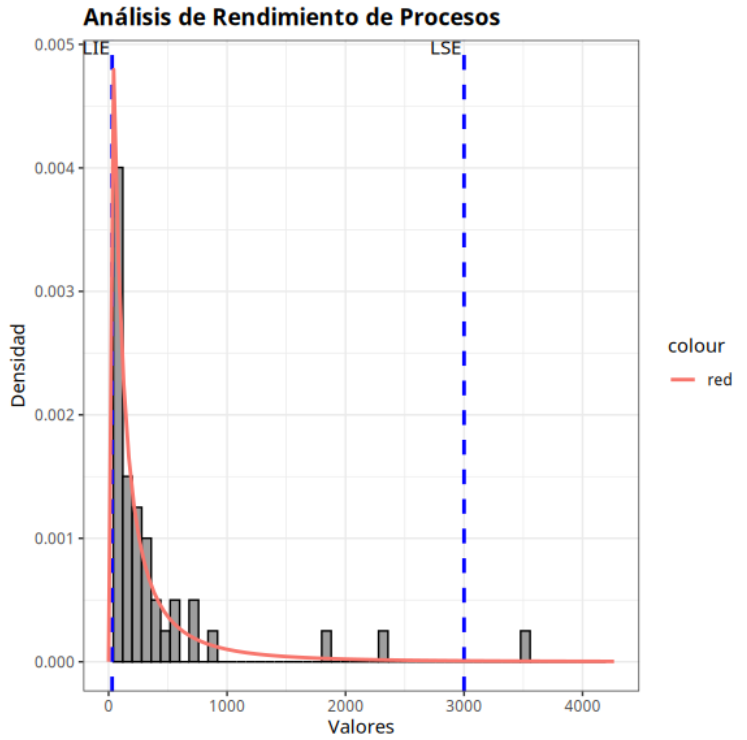
Los resultados son:
Especificaciones
| Valor | |
|---|---|
| Muestra: | 50 |
| Límite inferior | 30 |
| Límite superior | 3000 |
Estimaciones
| Parámetros | Valor |
|---|---|
| Media: | 358.584811836873 |
| Desviación Estándar: | 890.343884308414 |
Índices de Desempeño
| Índices de desempeño | |
|---|---|
| PP | 0.329 |
| PPI | 0.788 |
| PPS | 0.322 |
| PPk | 0.322 |
Índices observados
| Índices observados | |
|---|---|
| PPM > LSE | 20000 |
| PPM < LIE | 140000 |
| PPM total | 160000 |
Índices esperados
| Índices esperados | |
|---|---|
| PPM > LSE | 13367.0406498871 |
| PPM < LIS | 143137.013200317 |
| PPM total | 156504.053850204 |
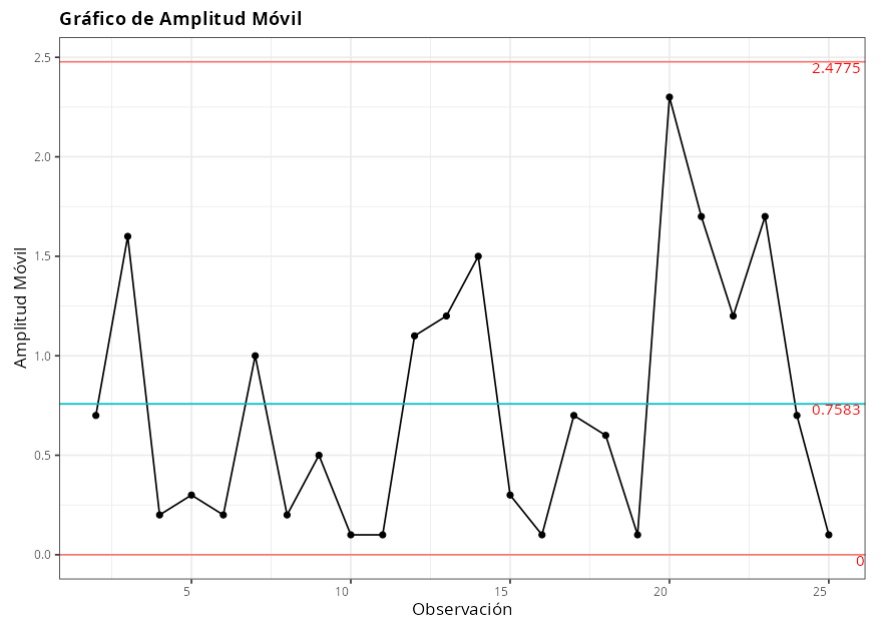
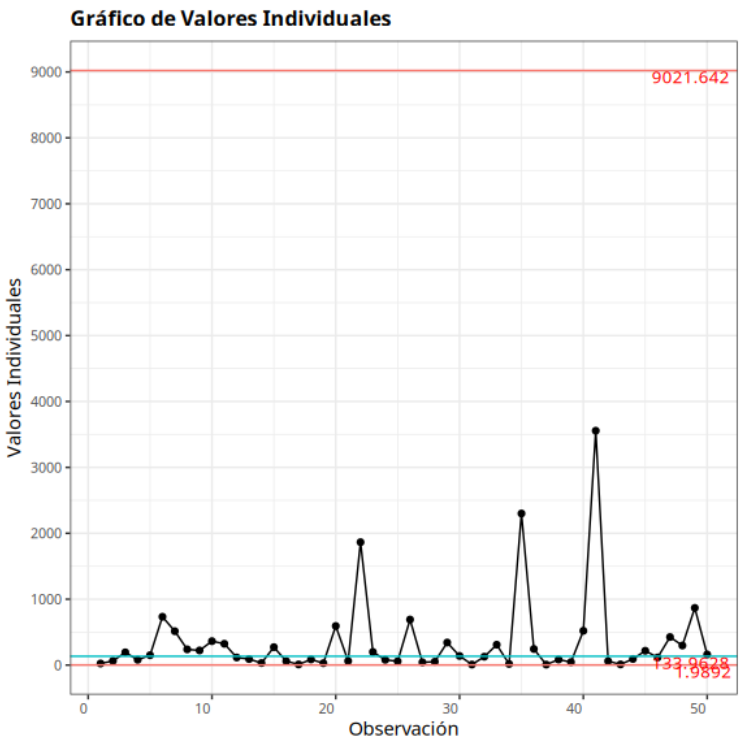
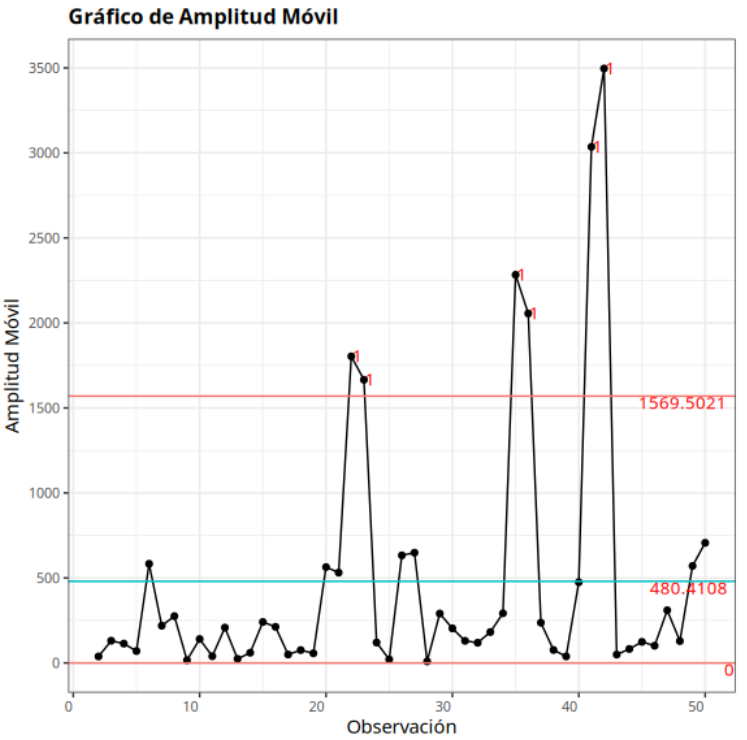
Puntos fuera de control - Gráfico de Amplitud en movimiento
| Subgrupo | Valor | Prueba |
|---|---|---|
| 22 | 1803.35 | 1 punto a más de 3 Sigmas de la línea central |
| 23 | 1665.79 | 1 punto a más de 3 Sigmas de la línea central |
| 35 | 2283.15 | 1 punto a más de 3 Sigmas de la línea central |
| 36 | 2055.74 | 1 punto a más de 3 Sigmas de la línea central |
| 41 | 3035.76 | 1 punto a más de 3 Sigmas de la línea central |
| 42 | 3496.41 | 1 punto a más de 3 Sigmas de la línea central |
Ejemplo 4:
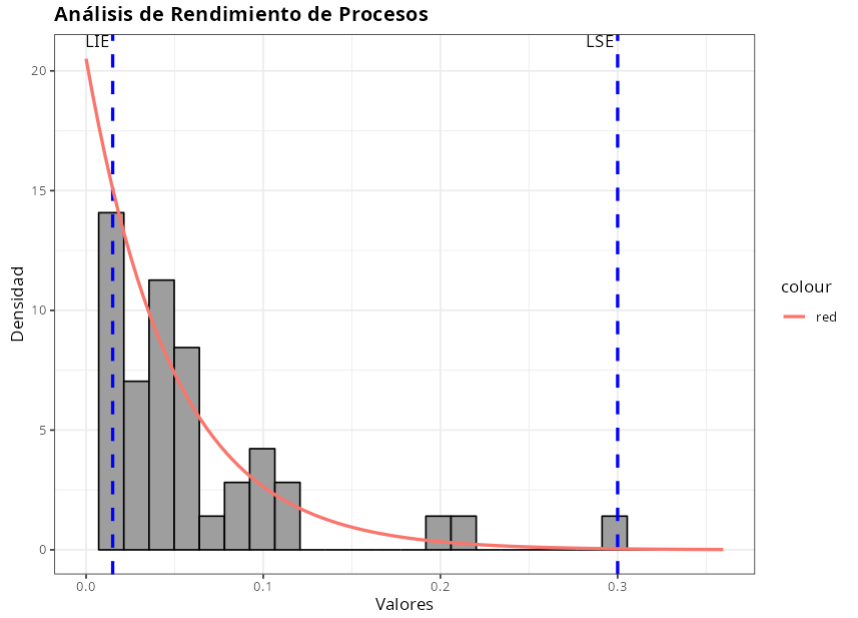
Considere los datos de la siguiente tabla para las dimensiones de una pieza en particular. Las especificaciones para estos datos son LSE = 0.3 y LIE = 0.0015.
| Medidas |
|---|
| 0.106 |
| 0.007 |
| 0.007 |
| 0.014 |
| 0.052 |
| 0.058 |
| 0.003 |
| 0.03 |
| 0.03 |
| 0.041 |
| 0.012 |
| 0.015 |
| 0.011 |
| 0.002 |
| 0.02 |
| 0.292 |
| 0.059 |
| 0.04 |
| 0.016 |
| 0.023 |
| 0.039 |
| 0.036 |
| 0.087 |
| 0.075 |
| 0.008 |
| 0.04 |
| 0.206 |
| 0.002 |
| 0.114 |
| 0.052 |
| 0.009 |
| 0.007 |
| 0.049 |
| 0.094 |
| 0.003 |
| 0.036 |
| 0.101 |
| 0.047 |
| 0.002 |
| 0.114 |
| 0.023 |
| 0.017 |
| 0.03 |
| 0.201 |
| 0.011 |
| 0.055 |
| 0.055 |
| 0.08 |
| 0.002 |
| 0.005 |
Subiremos los datos al sistema.
Realizaremos el análisis. y configuramos conforme la figura abajo.
- En “seleccionar pruebas” podemos elegir las pruebas que queremos realizar
En seguida, haga un clic en calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.
Los resultados son:
Especificaciones
| Valor | |
|---|---|
| Muestra: | 50 |
| Límite inferior | 0.0015 |
| Límite superior | 0.3 |
Estimativas
| Parámetros | Valor |
|---|---|
| Media: | 20.5086136177194 |
| Desviación Estándar: | 20.5086136177194 |
Índices de Desempeño
| Índices de desempeño | |
|---|---|
| PP | 0.927 |
| PPI | 0.957 |
| PPS | 0.923 |
| PPk | 0.923 |
Índices Observados
| Índices observados | |
|---|---|
| PPM > LSE | 0 |
| PPM < LIE | 0 |
| PPM total | 0 |
Índices esperados
| Índices esperados | |
|---|---|
| PPM > LSE | 2127.97578815149 |
| PPM < LIE | 30294.556820991 |
| PPM total | 32422.5326091425 |
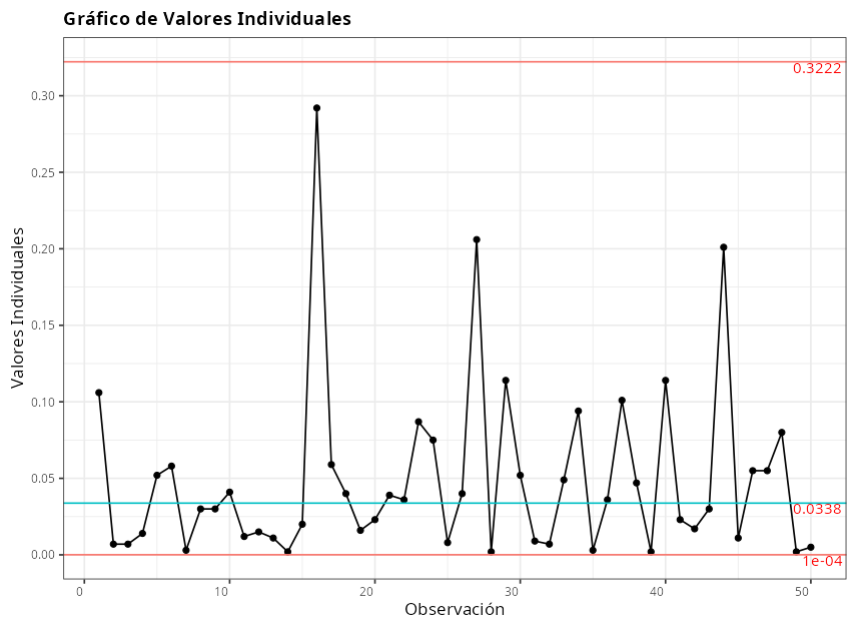
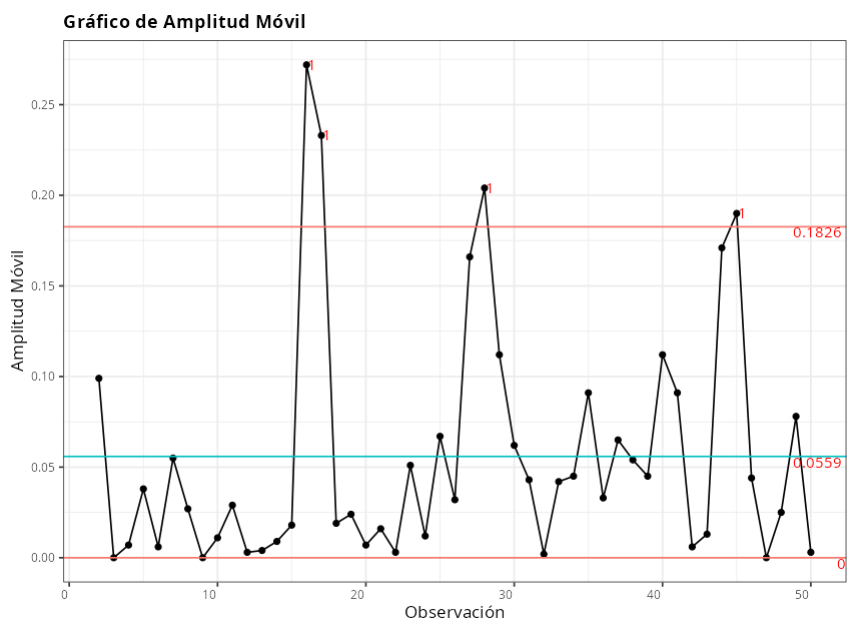
Puntos fuera de control - Gráfico de Amplitud en movimiento
| Subgrupo | Valor | Prueba |
|---|---|---|
| 16 | 0.272 | 1 punto a más de 3 Sigma de la línea central |
| 17 | 0.233 | 1 punto a más de 3 Sigma de la línea central |
| 28 | 0.204 | 1 punto a más de 3 Sigma de la línea central |
| 45 | 0.190 | 1 punto a más de 3 Sigma de la línea central |