5. Gráficos de lotes pequeños
Para lograr la eficiencia del proceso en lotes pequeños, es esencial que los métodos de CEP puedan verificar que el proceso está realmente bajo control estadístico, es decir, si es previsible y si pueden detectarse variaciones debidas a causas especiales durante estos pequeños "lotes".
Ejemplo 1:
En el mecanizado en bruto de diámetros exteriores (ejes) en un torno, se tomaron 25 muestras, cada una de ellas compuesta por 3 piezas, y se obtuvieron los valores de la tabla siguiente.
| Muestra | N | Pieza | P1 | P2 | P3 |
|---|---|---|---|---|---|
| 1 | 220 | 1 | 219.7838 | 220.0287 | 220.0922 |
| 2 | 220 | 1 | 219.9046 | 220.1229 | 220.2368 |
| 3 | 220 | 1 | 219.8345 | 220.0862 | 219.9268 |
| 4 | 220 | 1 | 219.7302 | 220.001 | 220.0357 |
| 5 | 220 | 1 | 220.1644 | 220.3151 | 219.9806 |
| 6 | 260 | 2 | 259.8635 | 260.1847 | 259.867 |
| 7 | 260 | 2 | 259.7917 | 259.9042 | 259.908 |
| 8 | 260 | 2 | 259.8264 | 259.8535 | 259.6465 |
| 9 | 260 | 2 | 259.6421 | 260.0869 | 259.9488 |
| 10 | 260 | 2 | 259.8945 | 260.0154 | 260.3685 |
| 11 | 320 | 3 | 319.7366 | 319.5236 | 319.7053 |
| 12 | 320 | 3 | 319.8834 | 319.415 | 319.8163 |
| 13 | 320 | 3 | 320.2431 | 320.1935 | 319.9893 |
| 14 | 320 | 3 | 319.9805 | 320.0828 | 320.0418 |
| 15 | 320 | 3 | 320.4944 | 320.4552 | 320.0477 |
| 16 | 240 | 4 | 239.8076 | 239.7787 | 240.2064 |
| 17 | 240 | 4 | 240.1663 | 240.1888 | 240.2023 |
| 18 | 240 | 4 | 240.1662 | 240.1382 | 240.1141 |
| 19 | 240 | 4 | 240.017 | 239.9212 | 240.0397 |
| 20 | 240 | 4 | 240.2081 | 240.0484 | 239.9119 |
| 21 | 300 | 5 | 300.0479 | 300.1325 | 299.9955 |
| 22 | 300 | 5 | 300.2815 | 299.9451 | 300.0365 |
| 23 | 300 | 5 | 299.7173 | 300.383 | 300.4608 |
| 24 | 300 | 5 | 300.0009 | 300.0487 | 300.0038 |
| 25 | 300 | 5 | 299.5822 | 300.4351 | 299.7919 |
Subiremos los datos al sistema
Realizaremos el análisis, y configuramos conforme la figura abajo.

En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.
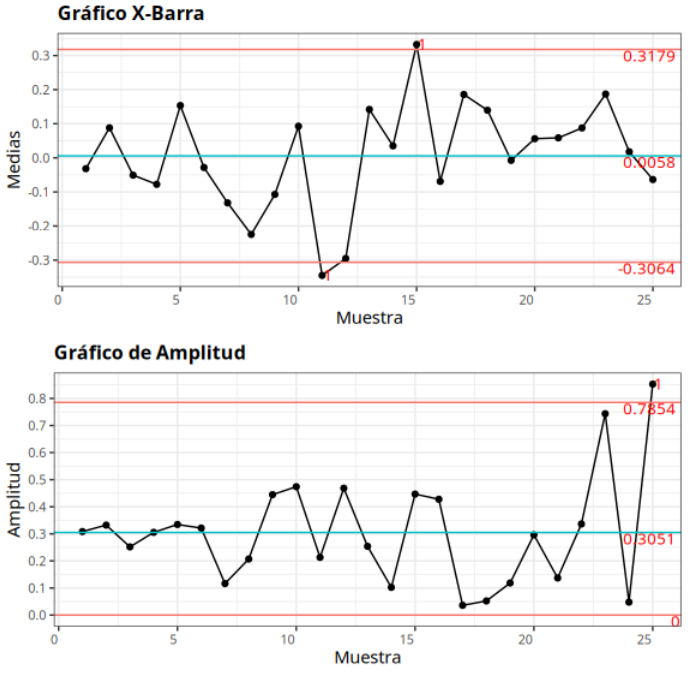
Los resultados son:
Límites - X-barra
| Límites | |
|---|---|
| Límite superior | 0.318 |
| Línea central | 0.006 |
| Límite inferior | -0.306 |
Límites - R
| Límites | |
|---|---|
| Desviación estándar | 0.180 |
| Límite superior | 0.785 |
| Línea central | 0.305 |
| Límite inferior | 0.000 |
Ejemplo 2:
En el mecanizado en bruto de diámetros exteriores (ejes) en un torno, se tomaron 25 muestras, cada una de ellas compuesta por 3 piezas, y se obtuvieron los valores de la tabla siguiente.
| Muestra | N | Pieza | P1 | P2 | P3 |
|---|---|---|---|---|---|
| 1 | 220 | 1 | 219.7838 | 220.0287 | 220.0922 |
| 2 | 220 | 1 | 219.9046 | 220.1229 | 220.2368 |
| 3 | 220 | 1 | 219.8345 | 220.0862 | 219.9268 |
| 4 | 220 | 1 | 219.7302 | 220.001 | 220.0357 |
| 5 | 220 | 1 | 220.1644 | 220.3151 | 219.9806 |
| 6 | 260 | 2 | 259.8635 | 260.1847 | 259.867 |
| 7 | 260 | 2 | 259.7917 | 259.9042 | 259.908 |
| 8 | 260 | 2 | 259.8264 | 259.8535 | 259.6465 |
| 9 | 260 | 2 | 259.6421 | 260.0869 | 259.9488 |
| 10 | 260 | 2 | 259.8945 | 260.0154 | 260.3685 |
| 11 | 320 | 3 | 319.7366 | 319.5236 | 319.7053 |
| 12 | 320 | 3 | 319.8834 | 319.415 | 319.8163 |
| 13 | 320 | 3 | 320.2431 | 320.1935 | 319.9893 |
| 14 | 320 | 3 | 319.9805 | 320.0828 | 320.0418 |
| 15 | 320 | 3 | 320.4944 | 320.4552 | 320.0477 |
| 16 | 240 | 4 | 239.8076 | 239.7787 | 240.2064 |
| 17 | 240 | 4 | 240.1663 | 240.1888 | 240.2023 |
| 18 | 240 | 4 | 240.1662 | 240.1382 | 240.1141 |
| 19 | 240 | 4 | 240.017 | 239.9212 | 240.0397 |
| 20 | 240 | 4 | 240.2081 | 240.0484 | 239.9119 |
| 21 | 300 | 5 | 300.0479 | 300.1325 | 299.9955 |
| 22 | 300 | 5 | 300.2815 | 299.9451 | 300.0365 |
| 23 | 300 | 5 | 299.7173 | 300.383 | 300.4608 |
| 24 | 300 | 5 | 300.0009 | 300.0487 | 300.0038 |
| 25 | 300 | 5 | 299.5822 | 300.4351 | 299.7919 |
Subiremos los datos al sistema.
Realizaremos el análisis, ajustando los datos conforme la figura de abajo.
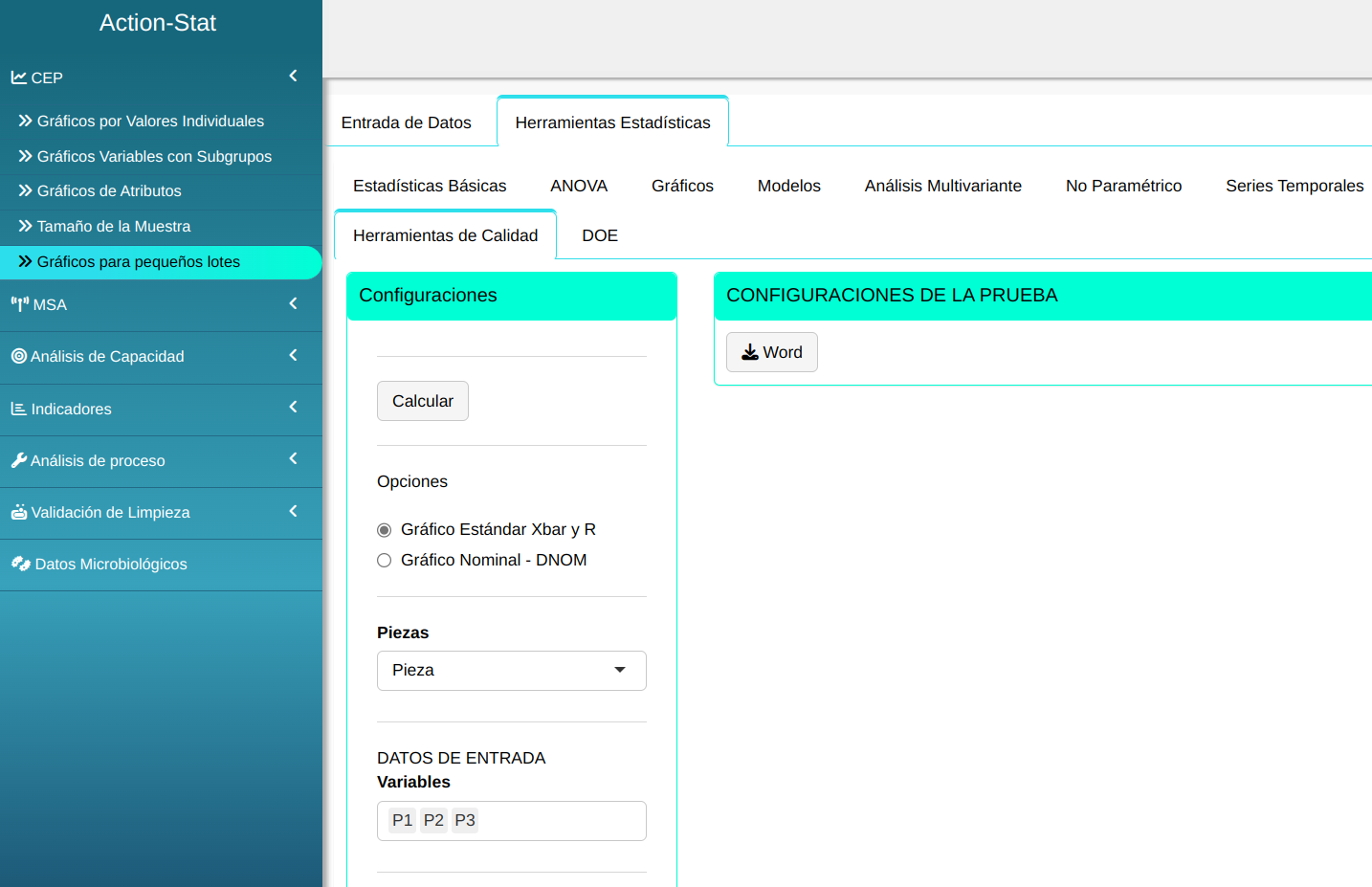

Al hacer clic en Calcular obtenemos los resultados y también se puede descargar el análisis en un archivo Word.
Los resultados son:
Estimados por pieza
| Piezas | Medias estandarizados | Amplitudes estandarizadas | Estimación de la desviación estándar |
|---|---|---|---|
| 1 | 220.016 | 0.306 | 0.181 |
| 2 | 259.920 | 0.313 | 0.185 |
| 3 | 319.974 | 0.297 | 0.175 |
| 4 | 240.061 | 0.186 | 0.110 |
| 5 | 300.058 | 0.424 | 0.250 |
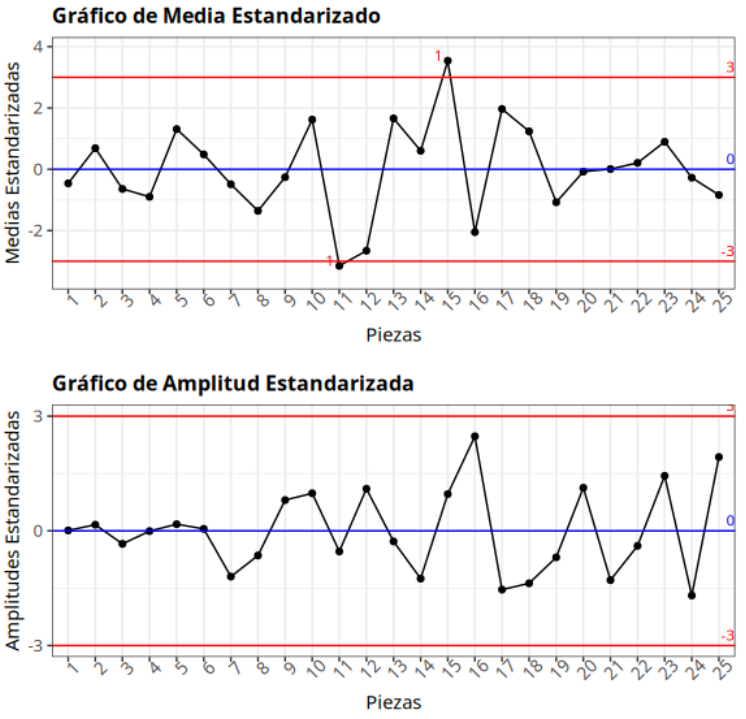
Estandarización por muestra
| Piezas | Medias Estandarizados | Amplitudes Estandarizadas | |
|---|---|---|---|
| 1 | 1 | -0.459 | 0.012 |
| 2 | 1 | 0.687 | 0.16 |
| 3 | 1 | -0.642 | -0.341 |
| 4 | 1 | -0.899 | -0.006 |
| 5 | 1 | 1.312 | 0.174 |
| 6 | 2 | 0.484 | 0.052 |
| 7 | 2 | -0.489 | -1.197 |
| 8 | 2 | -1.356 | -0.644 |
| 9 | 2 | -0.258 | 0.806 |
| 10 | 2 | 1.619 | 0.984 |
| 11 | 3 | -3.148 | -0.538 |
| 12 | 3 | -2.657 | 1.102 |
| 13 | 3 | 1.66 | -0.276 |
| 14 | 3 | 0.604 | -1.249 |
| 15 | 3 | 3.541 | 0.962 |
| 16 | 4 | -2.049 | 2.474 |
| 17 | 4 | 1.966 | -1.537 |
| 18 | 4 | 1.237 | -1.372 |
| 19 | 4 | -1.077 | -0.692 |
| 20 | 4 | -0.077 | 1.128 |
| 21 | 5 | 0.008 | -1.289 |
| 22 | 5 | 0.209 | -0.392 |
| 23 | 5 | 0.897 | 1.44 |
| 24 | 5 | -0.275 | -1.691 |
| 25 | 5 | -0.838 | 1.932 |