2. Método analítico
El método analítico para analizar el sistema de medición clasifica las piezas como defectuosas o no. Este método compara cada parte con un conjunto específico y acepta la pieza si se cumplen los límites; caso contrario, se rechaza la pieza.
Ejemplo:
Se está utilizando un dispositivo de medición de atributos para medir una dimensión que tiene una tolerancia de ±0.010. El dispositivo de medición se utiliza en inspección de final de línea 100% automática y se ve afectada por la repetibilidad y tendencia. Para realizar el estudio del dispositivo, medición de atributos, 8 piezas con medidas estándar en intervalos de 0.002 y -0.016 a -0.002 pasan por el dispositivo de medición 20 veces cada uno.
| Pieza | Medida | Aprobación | Total |
|---|---|---|---|
| 1 | -0.016 | 0 | 20 |
| 2 | -0.015 | 1 | 20 |
| 3 | -0.014 | 3 | 20 |
| 4 | -0.013 | 5 | 20 |
| 5 | -0.012 | 8 | 20 |
| 6 | -0.011 | 16 | 20 |
| 7 | -0.0105 | 18 | 20 |
| 8 | -0.01 | 20 | 20 |
| 9 | -0.008 | 20 | 20 |
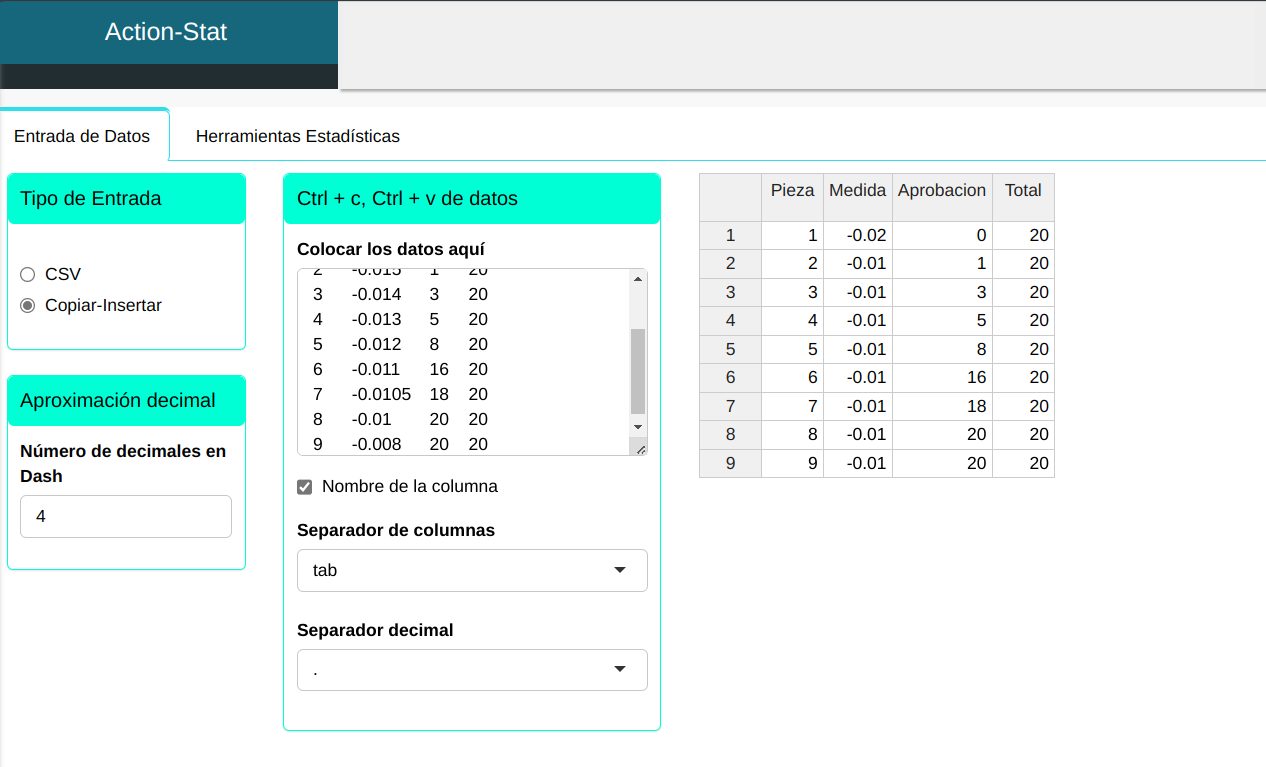
Subiremos los datos.
Realizaremos el análisis, ajustando los datos conforme la figura de abajo.
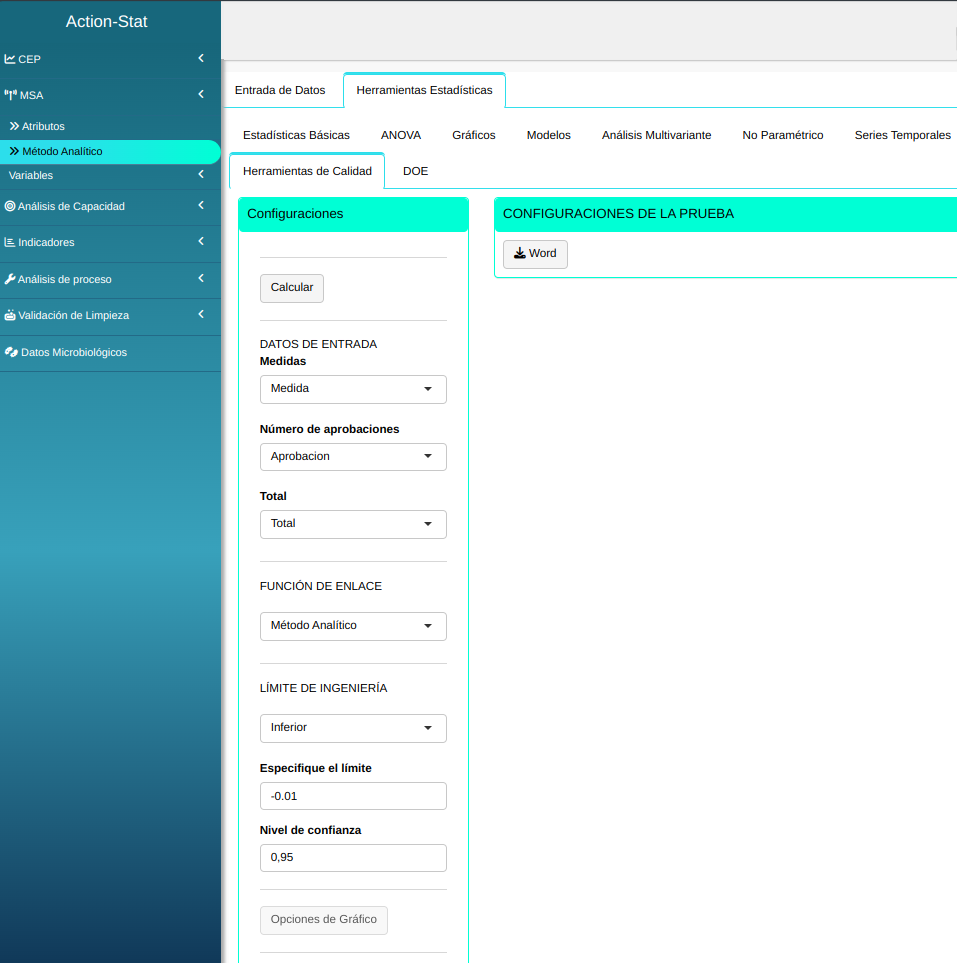
Clicando en Calcular obtenemos los resultados. También se puede generar y descargar los resultados en un archivo Word.
Los resultados son:
Estimación de la Probabilidad de aceptación
| Xi | Aprobación | Total | pi_i | Phi^{-1}(pi_i) | Prob. Pieza Aprobada |
|---|---|---|---|---|---|
| 0.006 | 0 | 20 | 0.025 | -1.960 | 0.0166 |
| 0.005 | 1 | 20 | 0.075 | -1.440 | 0.060 |
| 0.004 | 3 | 20 | 0.175 | -0.935 | 0.164 |
| 0.003 | 5 | 20 | 0.275 | -0.598 | 0.3439 |
| 0.002 | 8 | 20 | 0.425 | -0.189 | 0.5692 |
| 0.001 | 16 | 20 | 0.775 | 0.755 | 0.7736 |
| 0.0005 | 18 | 20 | 0.875 | 1.150 | 0.8505 |
| 0.000 | 20 | 20 | 0.975 | 1.960 | 0.9077 |
| -0.002 | 20 | 20 | 0.999 | 3.090 | 0.9934 |
–
Cuadro de prueba de tendencias
| V1 | |
|---|---|
| Hipótesis alternativa: Media diferente de | 0.000 |
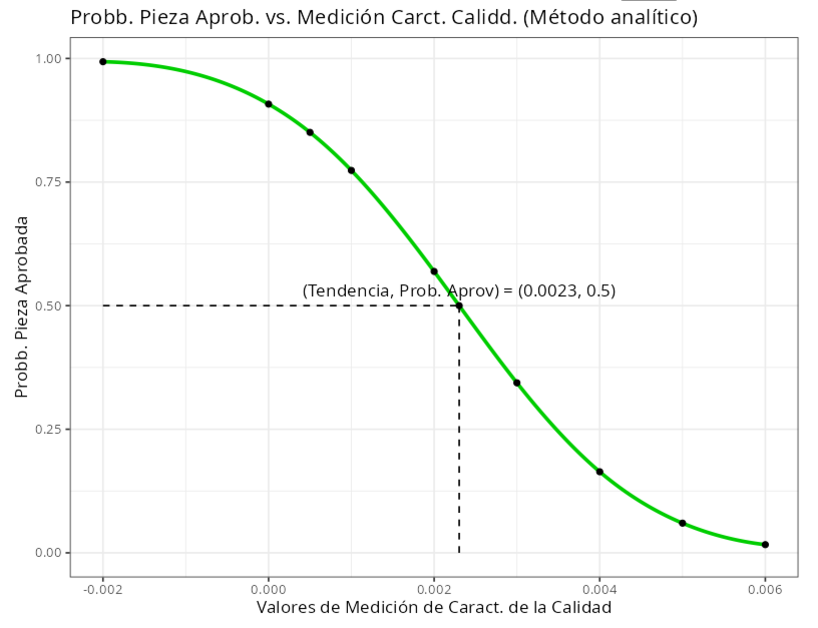
| Tendencia | 0.0023 |
| Desviación Estándar (sigma) | 0.0014 |
| Repetibilidad | 0.0073 |
| Estadística t | 9.840 |
| P-valor | 0.000 |
| Límite inferior | 0.0023 |
| Límite superior | 0.0023 |