3. Repetibilidad y Reproducibilidad
La repetibilidad y reproducibilidad es la suma de las variaciones debidas a falta de repetibilidad y reproducibilidad. Se pueden utilizar para estimar la variabilidad asociada al sistema de medición.
Ejemplo 1:
Consideremos un sistema de medición para medir el diámetro interior de un rodamiento. El ingeniero de calidad ha realizado un experimento con 10 piezas, 3 operarios y 3 repeticiones para cada operario y pieza. Los datos relativos a este experimento figuran en el siguiente cuadro.
| Medida | Pieza | Operador |
|---|---|---|
| 114.958 | 1 | 1 |
| 114.957 | 2 | 1 |
| 114.962 | 3 | 1 |
| 114.963 | 4 | 1 |
| 114.965 | 5 | 1 |
| 114.963 | 6 | 1 |
| 114.967 | 7 | 1 |
| 114.963 | 8 | 1 |
| 114.953 | 9 | 1 |
| 114.967 | 10 | 1 |
| 114.957 | 1 | 1 |
| 114.958 | 2 | 1 |
| 114.962 | 3 | 1 |
| 114.963 | 4 | 1 |
| 114.965 | 5 | 1 |
| 114.962 | 6 | 1 |
| 114.967 | 7 | 1 |
| 114.968 | 8 | 1 |
| 114.952 | 9 | 1 |
| 114.967 | 10 | 1 |
| 114.958 | 1 | 1 |
| 114.958 | 2 | 1 |
| 114.953 | 3 | 1 |
| 114.965 | 4 | 1 |
| 114.967 | 5 | 1 |
| 114.962 | 6 | 1 |
| 114.967 | 7 | 1 |
| 114.968 | 8 | 1 |
| 114.953 | 9 | 1 |
| 114.966 | 10 | 1 |
| 114.962 | 1 | 2 |
| 114.956 | 2 | 2 |
| 114.963 | 3 | 2 |
| 114.965 | 4 | 2 |
| 114.966 | 5 | 2 |
| 114.965 | 6 | 2 |
| 114.969 | 7 | 2 |
| 114.97 | 8 | 2 |
| 114.955 | 9 | 2 |
| 114.965 | 10 | 2 |
| 114.961 | 1 | 2 |
| 114.957 | 2 | 2 |
| 114.963 | 3 | 2 |
| 114.966 | 4 | 2 |
| 114.967 | 5 | 2 |
| 114.963 | 6 | 2 |
| 114.97 | 7 | 2 |
| 114.968 | 8 | 2 |
| 114.955 | 9 | 2 |
| 114.964 | 10 | 2 |
| 114.961 | 1 | 2 |
| 114.96 | 2 | 2 |
| 114.963 | 3 | 2 |
| 114.966 | 4 | 2 |
| 114.968 | 5 | 2 |
| 114.965 | 6 | 2 |
| 114.968 | 7 | 2 |
| 114.969 | 8 | 2 |
| 114.953 | 9 | 2 |
| 114.965 | 10 | 2 |
| 114.958 | 1 | 3 |
| 114.96 | 2 | 3 |
| 114.965 | 3 | 3 |
| 114.966 | 4 | 3 |
| 114.967 | 5 | 3 |
| 114.964 | 6 | 3 |
| 114.97 | 7 | 3 |
| 114.97 | 8 | 3 |
| 114.955 | 9 | 3 |
| 114.966 | 10 | 3 |
| 114.958 | 1 | 3 |
| 114.959 | 2 | 3 |
| 114.965 | 3 | 3 |
| 114.965 | 4 | 3 |
| 114.966 | 5 | 3 |
| 114.965 | 6 | 3 |
| 114.97 | 7 | 3 |
| 114.97 | 8 | 3 |
| 114.954 | 9 | 3 |
| 114.966 | 10 | 3 |
| 114.958 | 1 | 3 |
| 114.958 | 2 | 3 |
| 114.964 | 3 | 3 |
| 114.965 | 4 | 3 |
| 114.966 | 5 | 3 |
| 114.965 | 6 | 3 |
| 114.969 | 7 | 3 |
| 114.971 | 8 | 3 |
| 114.955 | 9 | 3 |
| 114.967 | 10 | 3 |
Subiremos los datos al sistema.
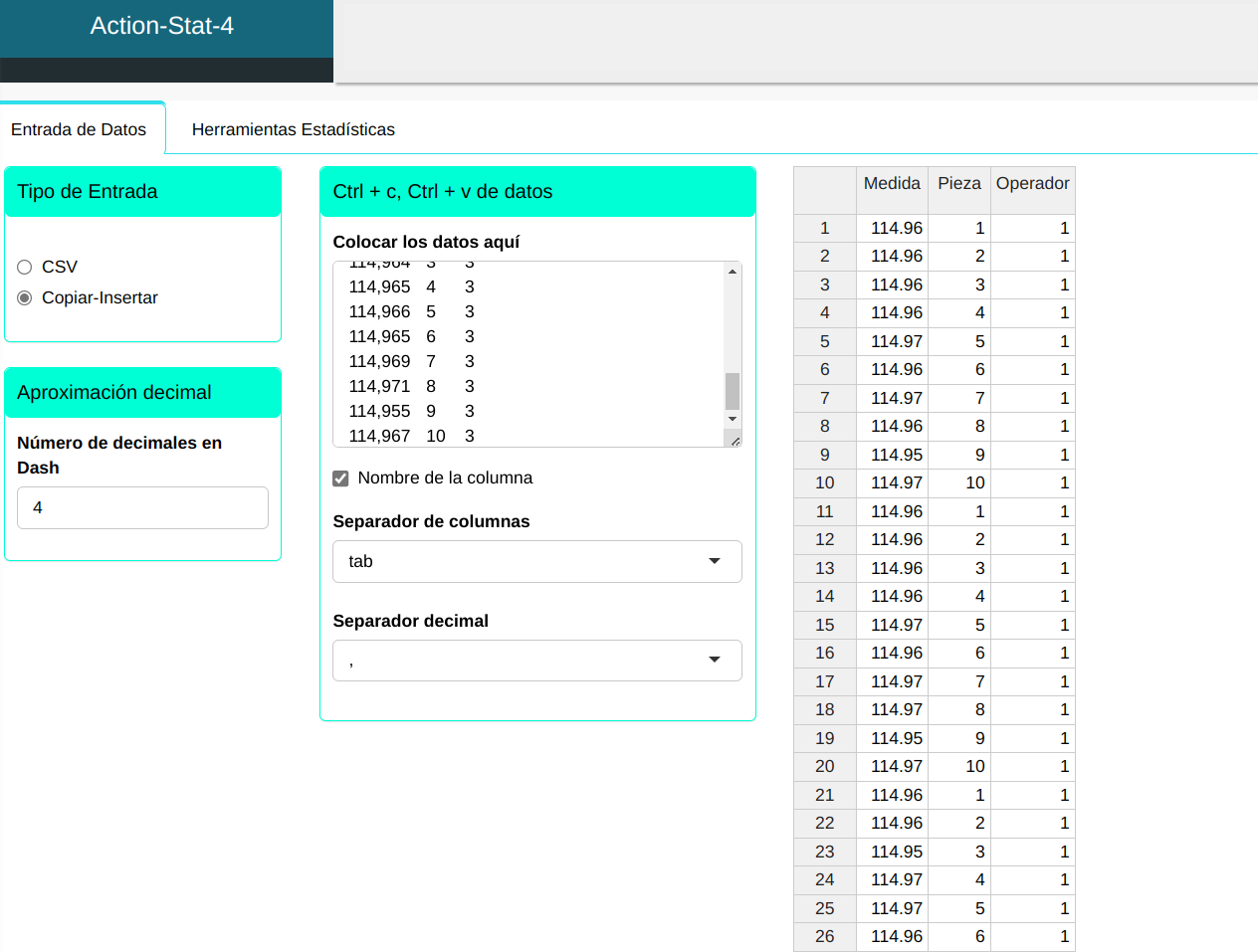
Para realizar el análisis. ajustamos conforme la figura abajo.
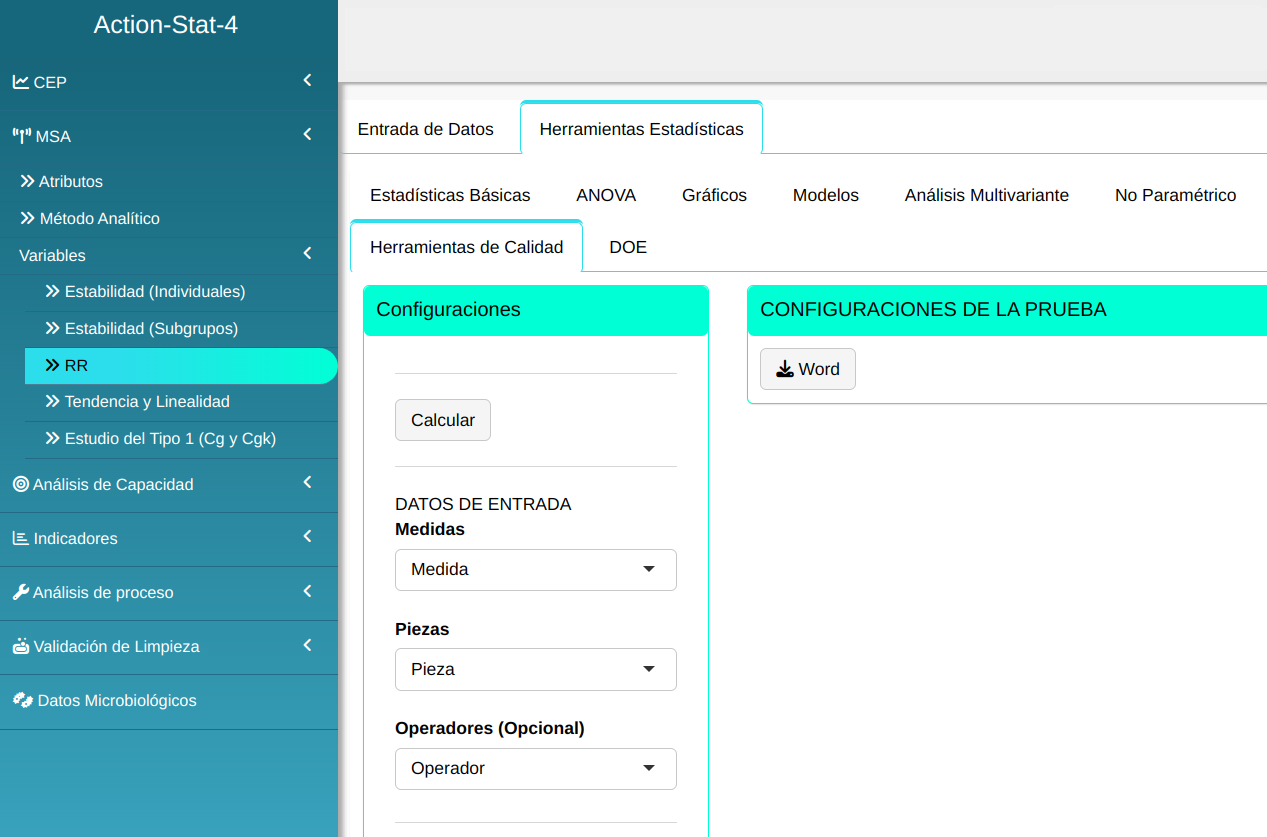
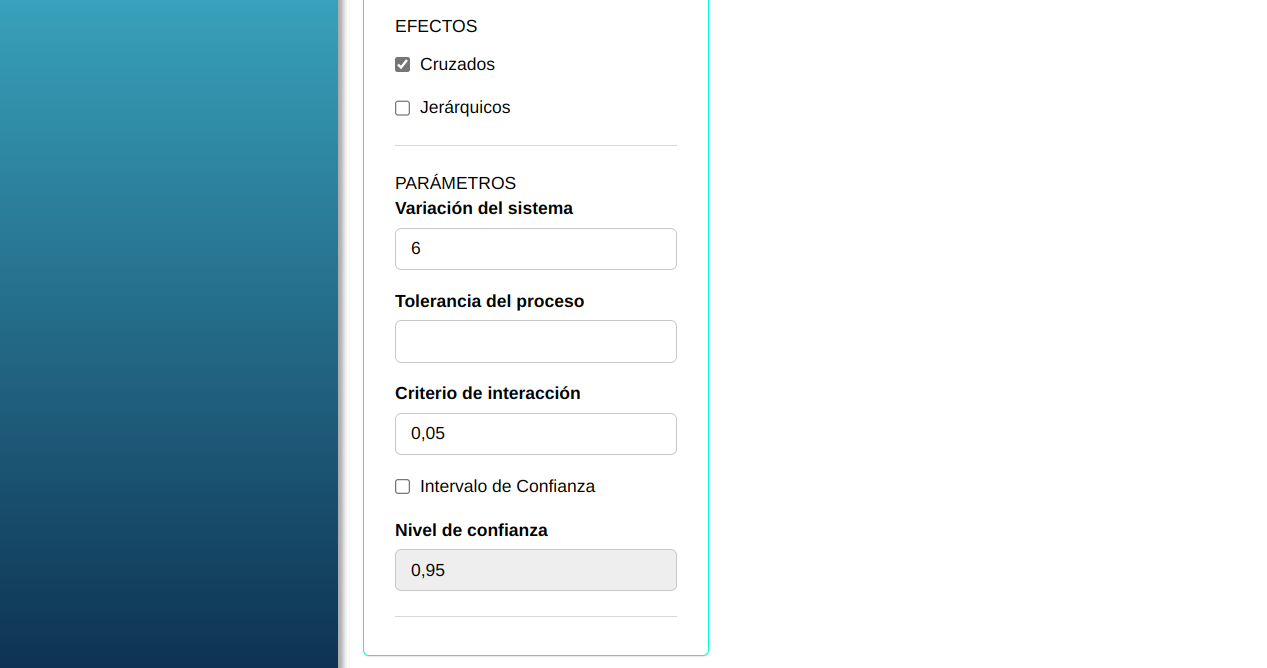
Para ver los resultados y obtenerlos en un archivo de Word, presione calcular.
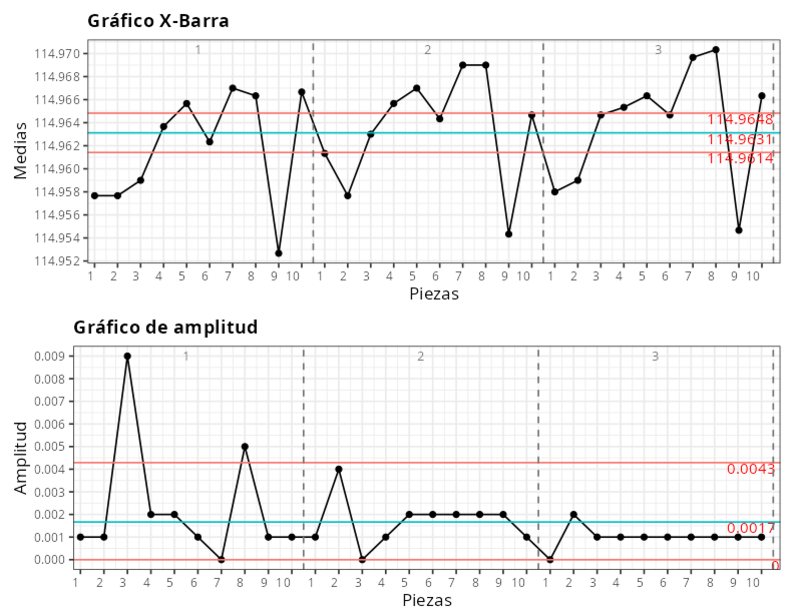
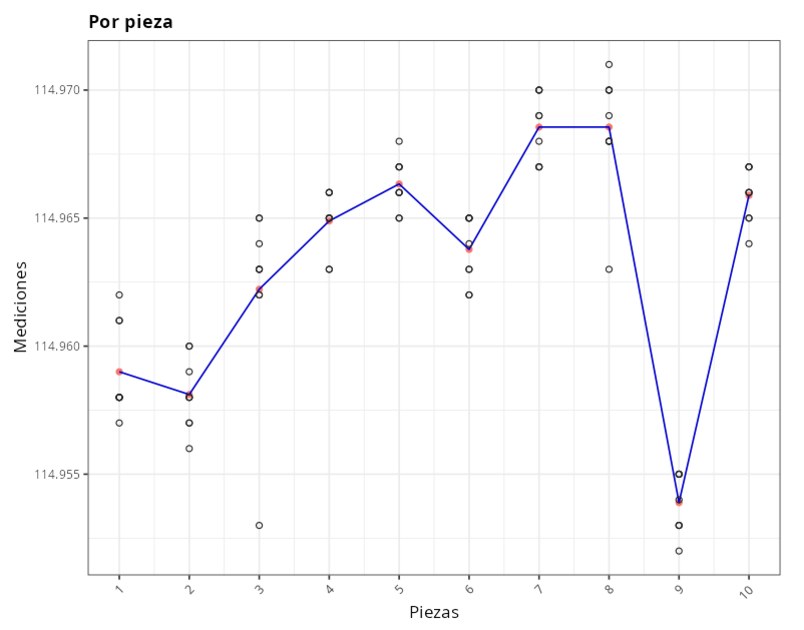
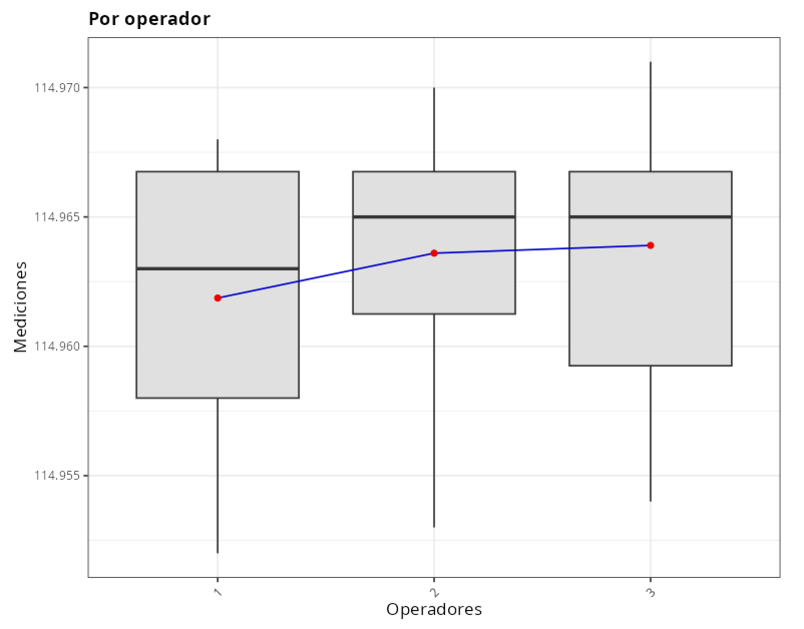
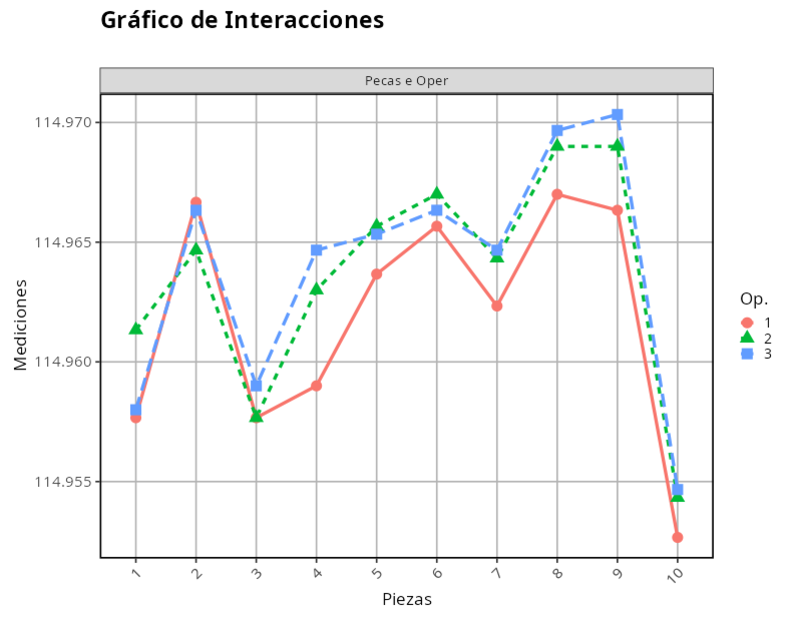
Los resultados son:
CUADRO ANOVA
| G.L. | Suma de cuadrados | Cuadrados Medios | Estadística F | P-Valor |
|---|---|---|---|---|
| Piezas | 9 | 0.0019 | 0.0002 | 0 |
| Operadores | 2 | 0.0001 | 0 | 0.0025 |
| Interacción | 18 | 0.0001 | 0 | 0.0074 |
| Repetibilidad | 60 | 0.0001 | 0 |
CUADRO DE CONTRIBUCIONES
| Varianzas | Contribución (%) | |
|---|---|---|
| Repetibilidad | 0 | 6.8594 |
| Reproducibilidad | 0 | 7.0839 |
| Operadores | 0 | 4.0290 |
| Interacción | 0 | 3.0549 |
| Piezas | 0 | 86.0567 |
| Repetibilidad y reproducibilidad | 0 | 13.9433 |
| Total | 0 | 100 |
VARIACIÓN TOTAL Y/O TOLERANCIA
| Desviación Estándar | Variación total (%) | |
|---|---|---|
| Repetibilidad | 0.0013 | 26.1905 |
| Reproducibilidad | 0.0014 | 26.6155 |
| Operadores | 0.0010 | 20.0723 |
| Interacción | 0.0009 | 17.4782 |
| Piezas | 0.0048 | 92.7668 |
| Repetibilidad y reproducibilidad | 0.0019 | 37.3407 |
| Total | 0.0051 | 100 |
| Resultado del Análisis | ||
| $\qquad \quad$ NDC: 3 |
Ejemplo 2:
Considere un sistema de medición para medir el diámetro de una pieza. El ingeniero de calidad realizó un experimento con 15 piezas y 3 mediciones por pieza. Los datos relacionados con este experimento están disponibles en siguiente cuadro.
| Piezas | Medidas |
|---|---|
| 1 | 461.28 |
| 2 | 458.17 |
| 3 | 460.57 |
| 4 | 459.28 |
| 5 | 461.28 |
| 6 | 460.25 |
| 7 | 458.82 |
| 8 | 461.58 |
| 9 | 459.36 |
| 10 | 459.62 |
| 11 | 461.38 |
| 12 | 458.67 |
| 13 | 462.57 |
| 14 | 459.58 |
| 15 | 461.76 |
| 1 | 461.50 |
| 2 | 458.62 |
| 3 | 460.28 |
| 4 | 459.66 |
| 5 | 461.12 |
| 6 | 460.68 |
| 7 | 458.95 |
| 8 | 461.10 |
| 9 | 459.52 |
| 10 | 459.34 |
| 11 | 461.57 |
| 12 | 459.03 |
| 13 | 462.28 |
| 14 | 459.66 |
| 15 | 461.12 |
| 1 | 461.20 |
| 2 | 458.61 |
| 3 | 460.32 |
| 4 | 459.58 |
| 5 | 461.18 |
| 6 | 460.28 |
| 7 | 458.66 |
| 8 | 461.18 |
| 9 | 459.57 |
| 10 | 459.54 |
| 11 | 461.53 |
| 12 | 458.98 |
| 13 | 462.32 |
| 14 | 459.28 |
| 15 | 461.15 |
Subiremos los datos al sistema.
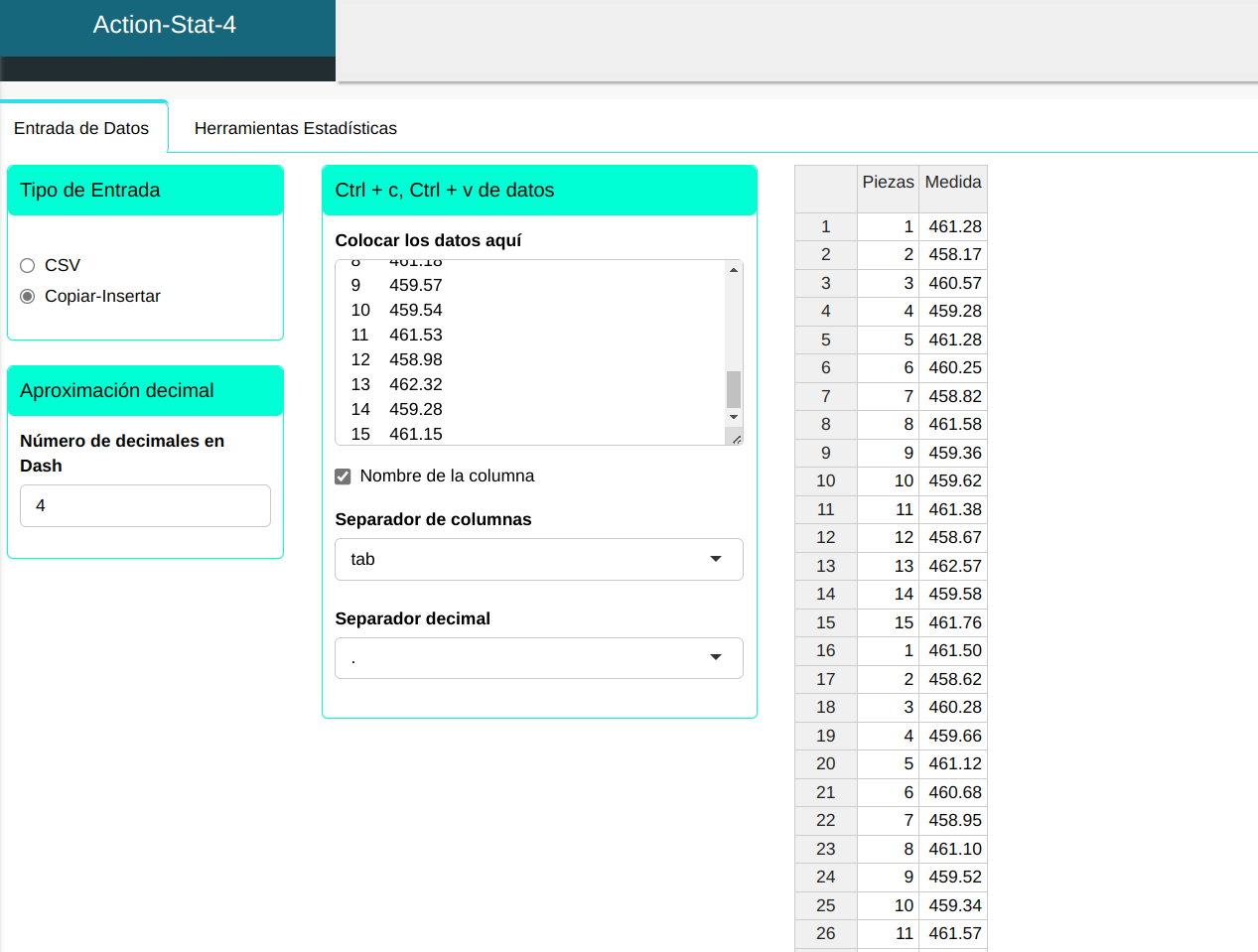
Para realizar el análisis. ajustamos conforme la figura abajo.
Para ver los resultados y obtenerlos en un archivo de Word, presione calcular.
Los resultados son:
CUADRO ANOVA
| G.L. | Suma de cuadrados | Cuadrados Medios | Estad. F | P-valor | |
|---|---|---|---|---|---|
| Piezas | 14 | 59.501 | 4.25001 | 109.43087 | 0 |
| Repetibilidad | 30 | 1.16513 | 0.03884 |
CUADRO DE CONTRIBUCIONES
| Varianza | Contribución (%) | |
|---|---|---|
| Repetibilidad | 0.039 | 2.692 |
| Piezas | 1.404 | 97.308 |
| Repetibilidad y reproducibilidad | 0.039 | 2.692 |
| Totales | 1.443 | 100.000 |
VARIACIÓN Y/O TOLERANCIA TOTAL
| Desviación Estándar | Variación total (%) | |
|---|---|---|
| Repetibilidad | 0.197 | 16.408 |
| Piezas | 1.185 | 98.645 |
| Repetibilidad y reproducibilidad | 0.197 | 16.408 |
| Totales | 1.201 | 100.000 |
| Resultado del Análisis | ||
| $\qquad \quad$ NDC: 8 |
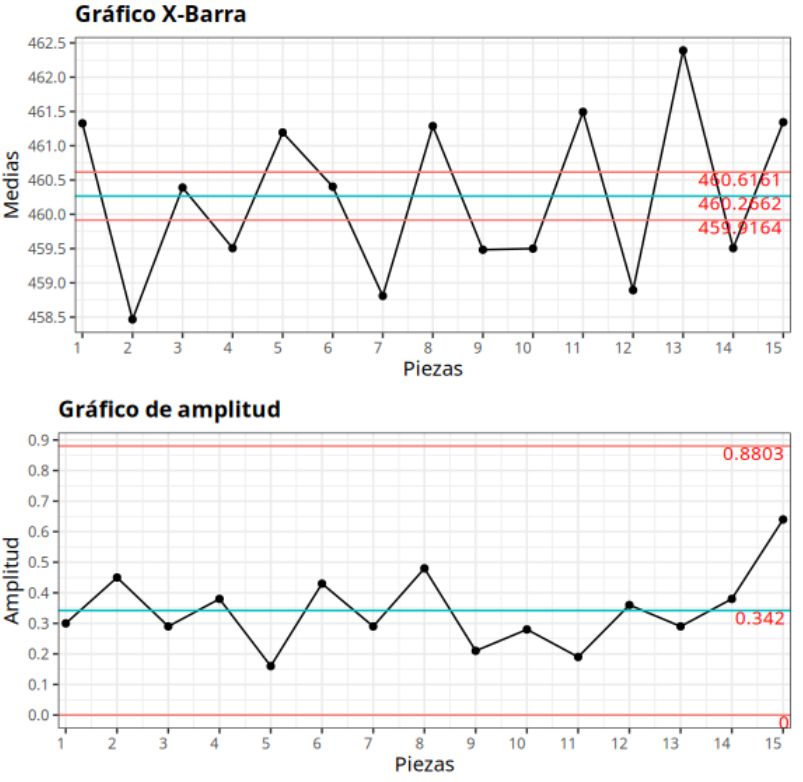
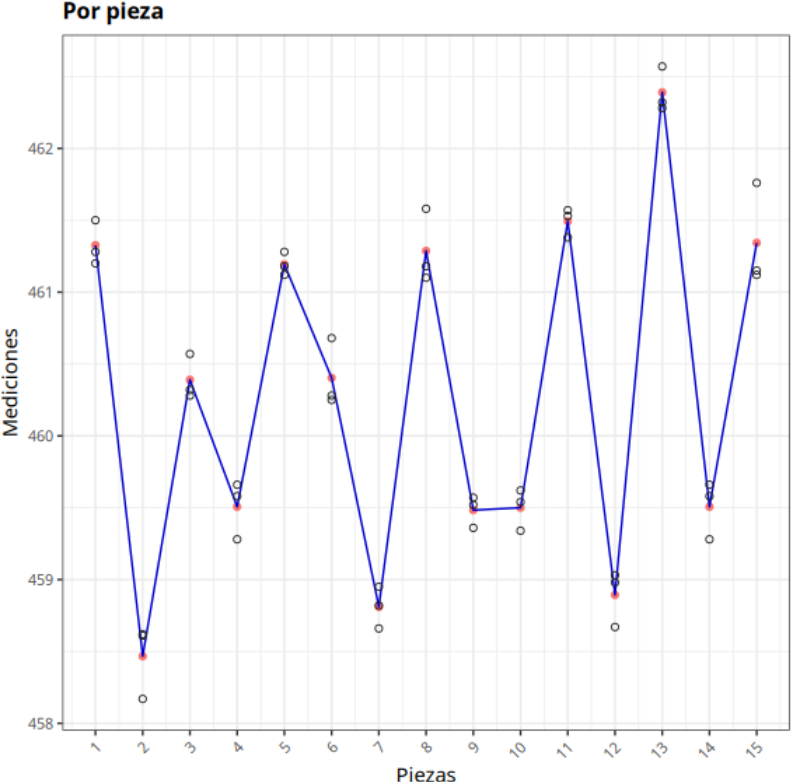
Ejemplo 3:
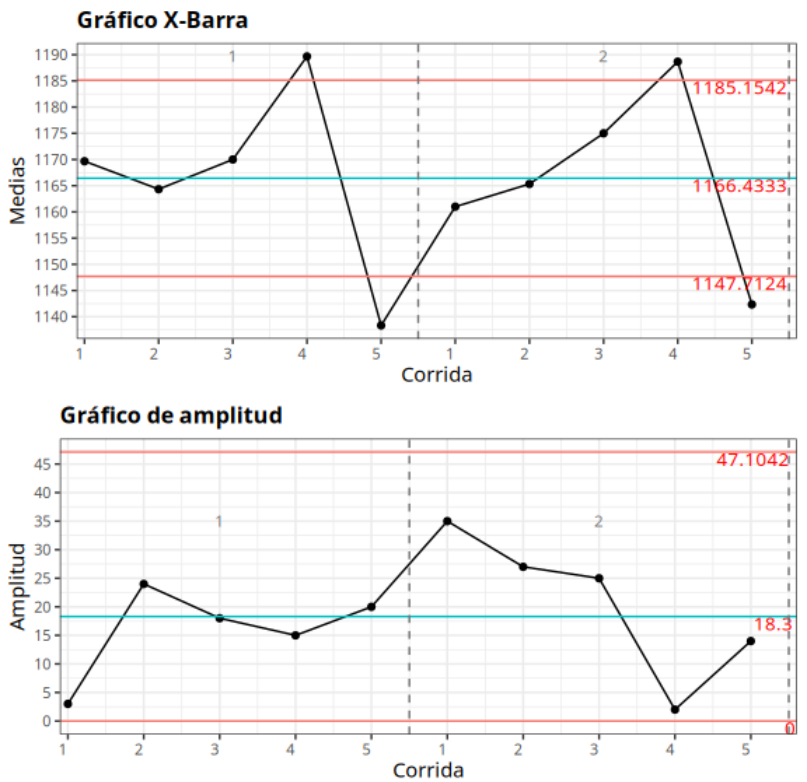
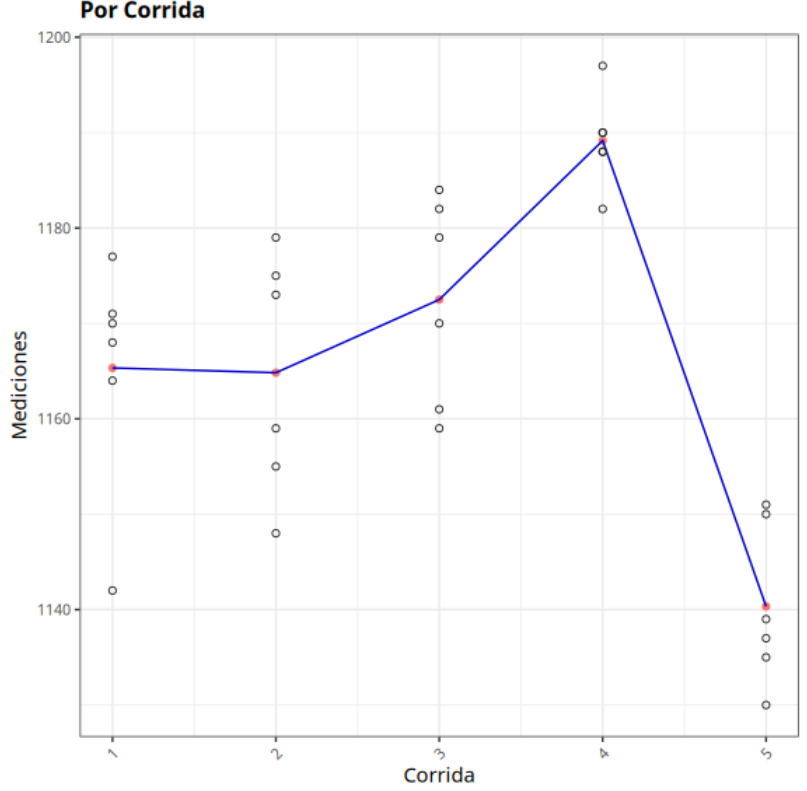
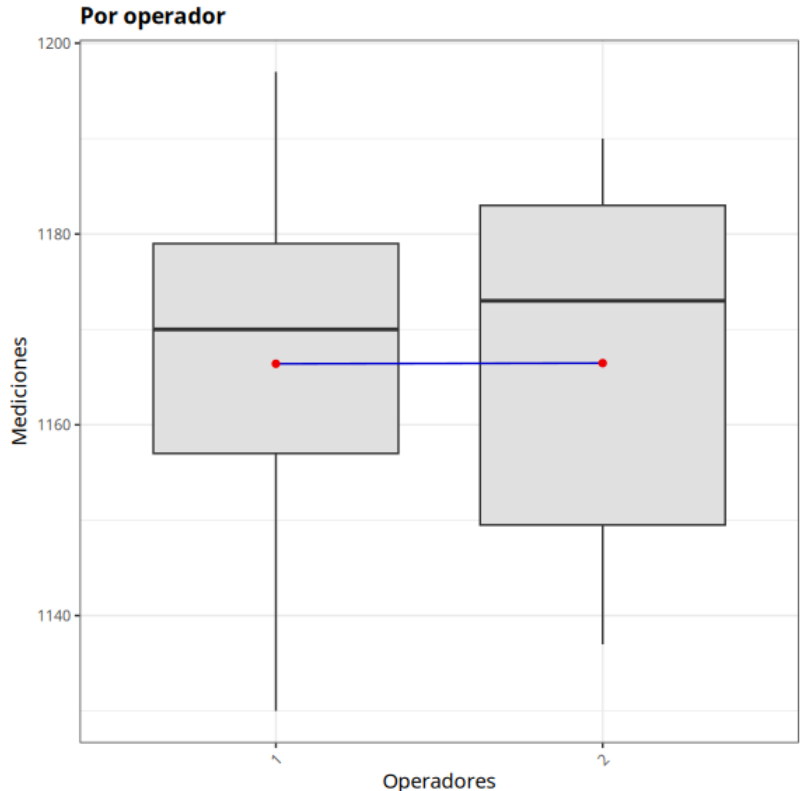
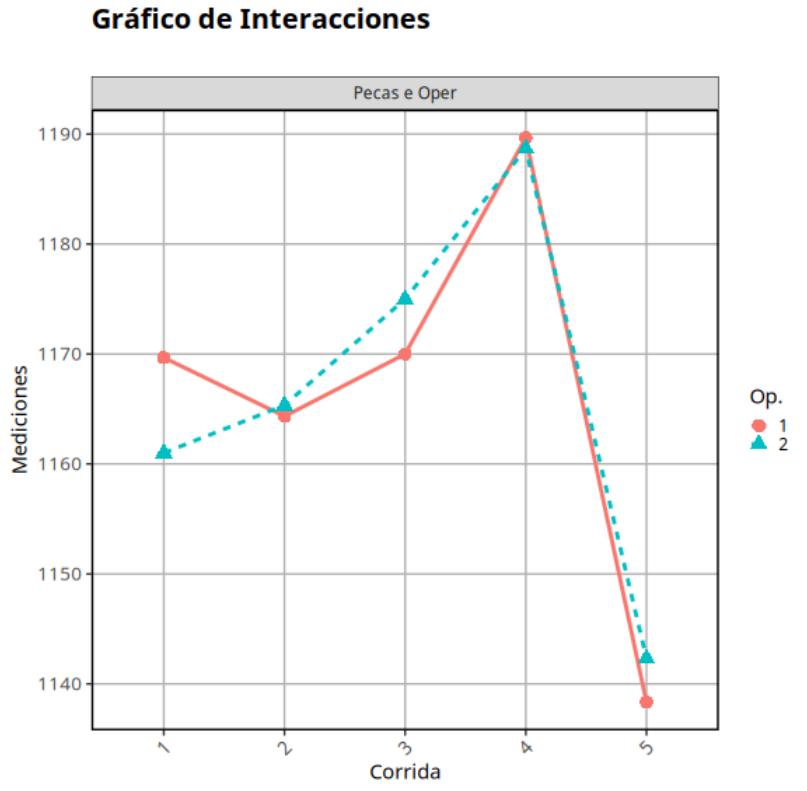
A continuación consideramos la característica de resistencia a la tracción realizada con muestras de acero. Se seleccionaron cinco series de acero. con poca variabilidad dentro de las series y variabilidad natural del proceso (producción) entre series. Se utilizaron dos operadores con 3 mediciones de cada ejecución por operador.
| Serie | Operador | Resistencia |
|---|---|---|
| 1 | 1 | 1168 |
| 1 | 1 | 1170 |
| 1 | 1 | 1171 |
| 2 | 1 | 1179 |
| 2 | 1 | 1155 |
| 2 | 1 | 1159 |
| 3 | 1 | 1161 |
| 3 | 1 | 1179 |
| 3 | 1 | 1170 |
| 4 | 1 | 1190 |
| 4 | 1 | 1182 |
| 4 | 1 | 1197 |
| 5 | 1 | 1135 |
| 5 | 1 | 1150 |
| 5 | 1 | 1130 |
| 1 | 2 | 1142 |
| 1 | 2 | 1164 |
| 1 | 2 | 1177 |
| 2 | 2 | 1173 |
| 2 | 2 | 1175 |
| 2 | 2 | 1148 |
| 3 | 2 | 1184 |
| 3 | 2 | 1159 |
| 3 | 2 | 1182 |
| 4 | 2 | 1190 |
| 4 | 2 | 1188 |
| 4 | 2 | 1188 |
| 5 | 2 | 1139 |
| 5 | 2 | 1137 |
| 5 | 2 | 1151 |
Subiremos los datos al sistema.
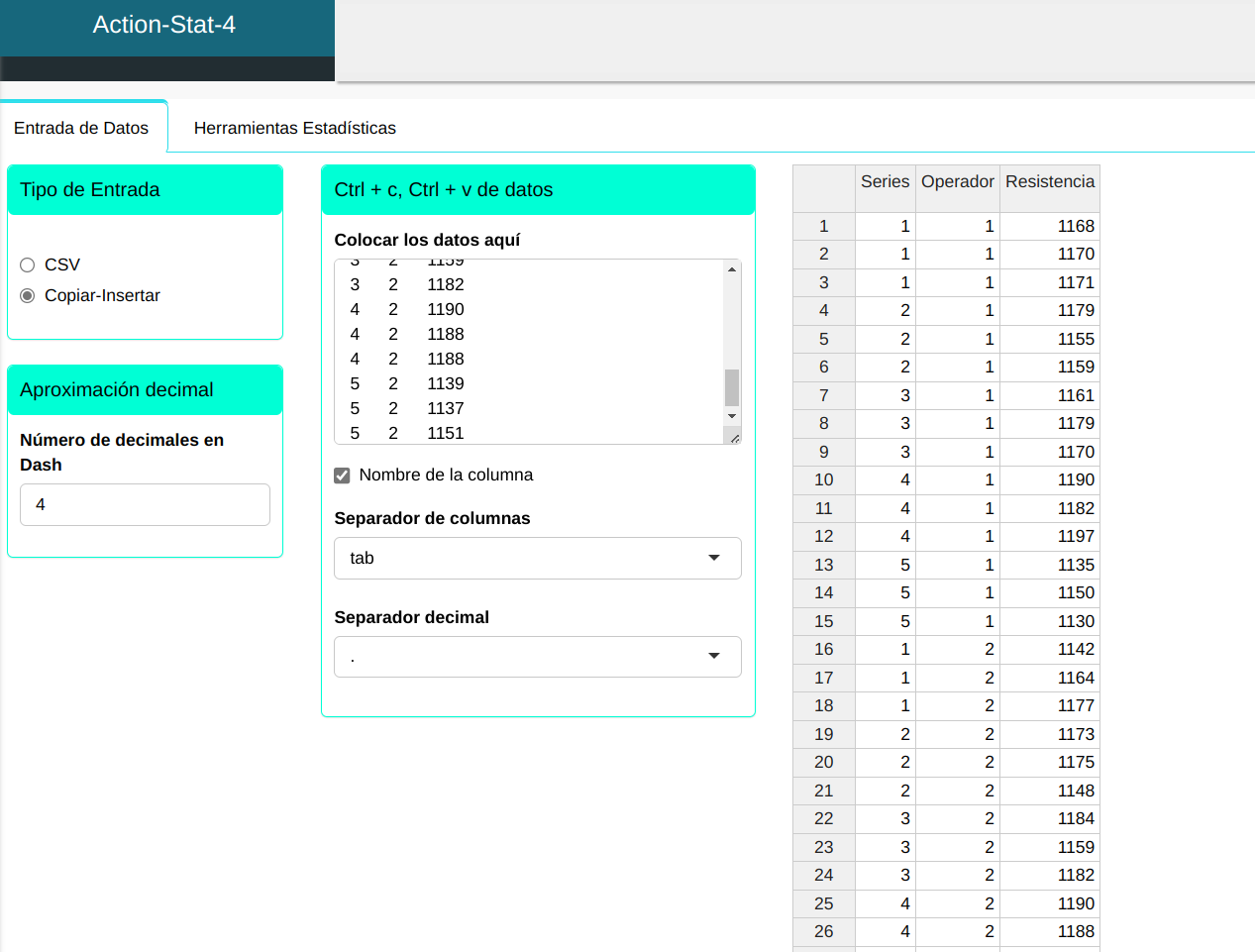
Para realizar el análisis. ajustamos conforme la figura abajo.
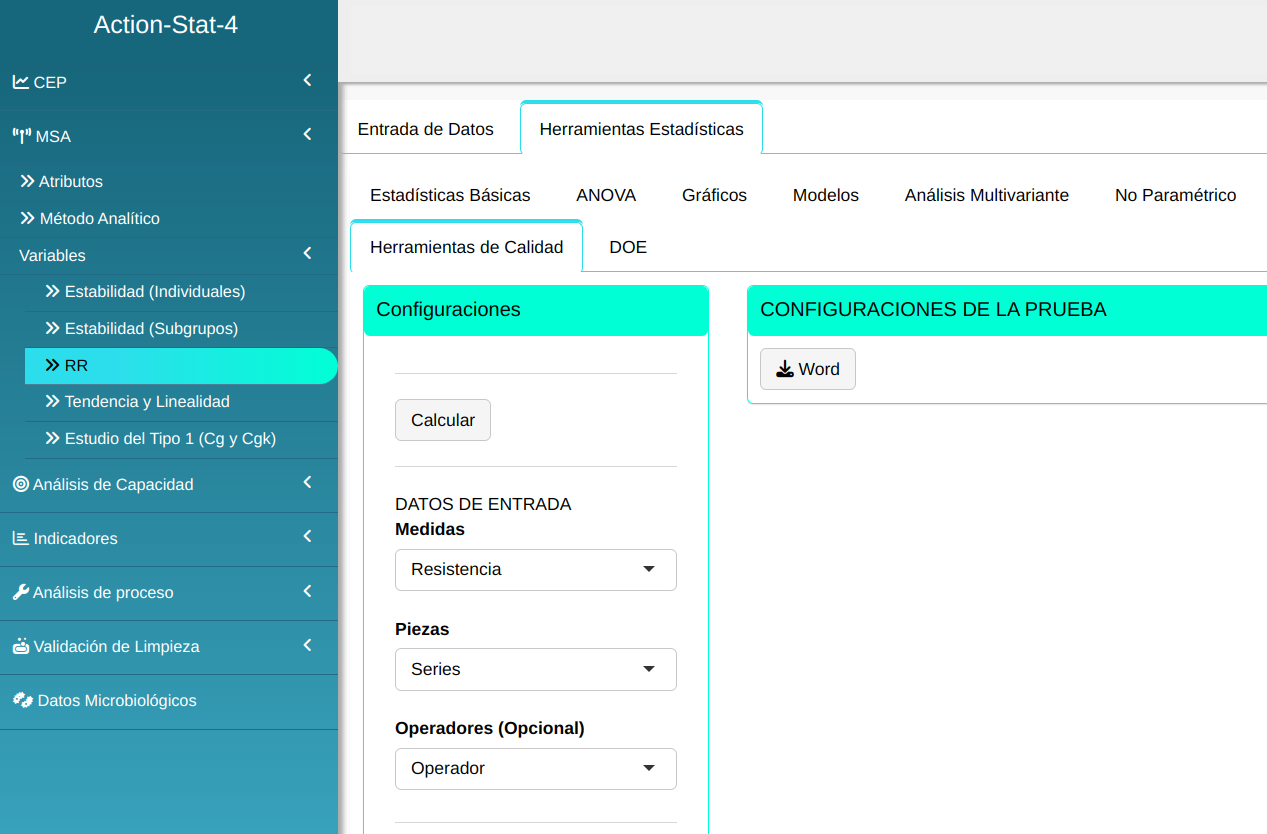
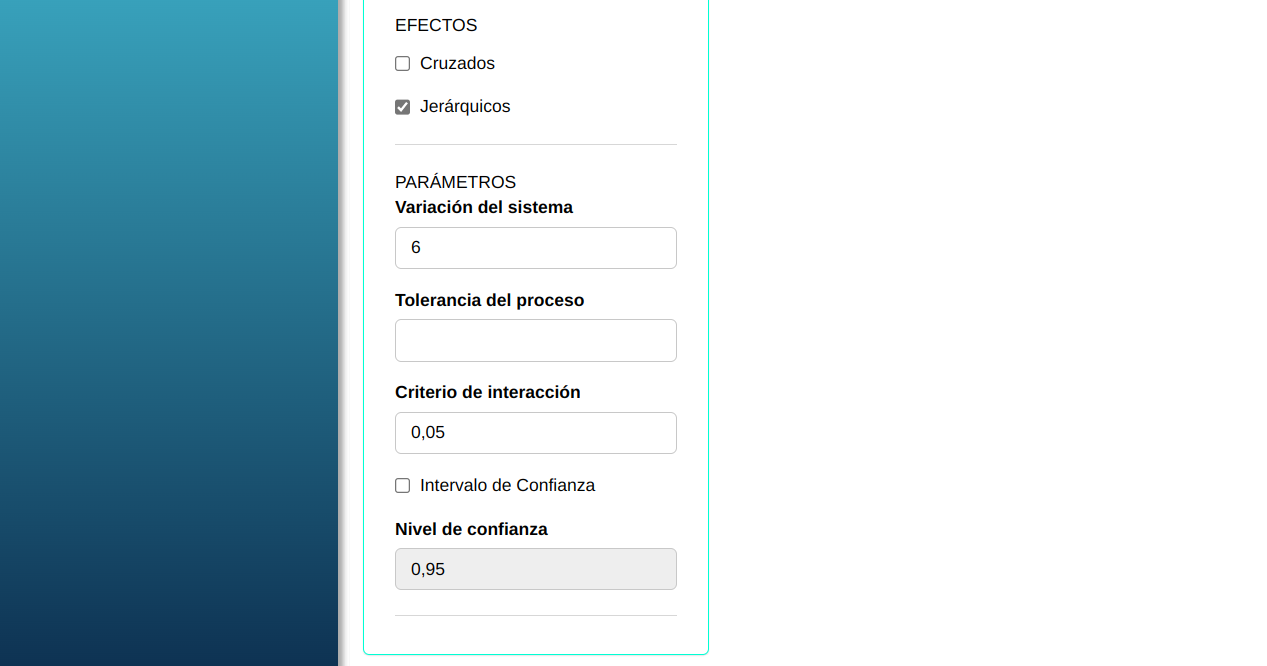
Para ver los resultados y obtenerlos en un archivo de Word, presione calcular.
Los resultados son:
TABLA ANOVA
| G.L | Suma de cuadrados | Cuadrados Medios | Estadística F | Valor P | |
|---|---|---|---|---|---|
| Operadores | 1 | 0.033 | 0.033 | 0.000 | 0.995 |
| Piezas/Operadores | 8 | 7608.667 | 951.083 | 7.897 | 0.000 |
| Repetibilidad | 20 | 2408.667 | 120.433 |
TABLA DE CONTRIBUCIONES
| Varianzas | Contribución (%) | |
|---|---|---|
| Repetibilidad | 120.433 | 30.312 |
| Reproducibilidad | 0.000 | 0.000 |
| Operadores | 0.000 | 0.000 |
| Piezas | 276.883 | 69.688 |
| Repetibilidad y reproducibilidad | 120.433 | 30.312 |
| Totales | 397.317 | 100.000 |
VARIACIÓN Y/O TOLERANCIA TOTAL
| Desviación estándar | Variación total (%) | |
|---|---|---|
| Repetibilidad | 10.974 | 55.056 |
| Reproducibilidad | 0.000 | 0.000 |
| Operadores | 0.000 | 0.000 |
| Piezas | 16.640 | 83.480 |
| Repetibilidad y reproducibilidad | 10.974 | 55.056 |
| Totales | 19.933 | 100.000 |
| Resultado del Análisis | ||
| $\qquad \quad$ NDC: 2 |