4. Tendencia y Linealidad
La linealidad se mide por la pendiente de la recta formada por los diferentes valores de referencia en relación con su tendencia. Cuanto menos inclinada sea la línea, mejor será la calidad de los sistemas de medición.
Ejemplo 1:
Como aplicación de un estudio de tendencia y linealidad, evaluaremos un sistema de medición para medir la temperatura de un horno mediante un pirómetro óptico. Para ello realizaremos un estudio comparativo con un elemento de término estándar. Tomamos 5 niveles de temperatura:
| Estándar | Medidas | VR | Tolerancia |
|---|---|---|---|
| 1 | 748.8 | 750 | 100 |
| 1 | 749.8 | 750 | 100 |
| 1 | 748.8 | 750 | 100 |
| 1 | 748.8 | 750 | 100 |
| 1 | 748.8 | 750 | 100 |
| 1 | 748.8 | 750 | 100 |
| 1 | 747.7 | 750 | 100 |
| 1 | 747.7 | 750 | 100 |
| 1 | 747.7 | 750 | 100 |
| 1 | 748.7 | 750 | 100 |
| 1 | 749.7 | 750 | 100 |
| 1 | 750.7 | 750 | 100 |
| 2 | 848.8 | 850 | 100 |
| 2 | 848.8 | 850 | 100 |
| 2 | 848.8 | 850 | 100 |
| 2 | 847.2 | 850 | 100 |
| 2 | 847.2 | 850 | 100 |
| 2 | 847.2 | 850 | 100 |
| 2 | 846.1 | 850 | 100 |
| 2 | 846.1 | 850 | 100 |
| 2 | 846.2 | 850 | 100 |
| 2 | 846.3 | 850 | 100 |
| 2 | 847.3 | 850 | 100 |
| 2 | 848.3 | 850 | 100 |
| 3 | 946.9 | 950 | 100 |
| 3 | 946.9 | 950 | 100 |
| 3 | 946.9 | 950 | 100 |
| 3 | 945.8 | 950 | 100 |
| 3 | 944.8 | 950 | 100 |
| 3 | 944.8 | 950 | 100 |
| 3 | 943.6 | 950 | 100 |
| 3 | 943.6 | 950 | 100 |
| 3 | 943.6 | 950 | 100 |
| 3 | 945.1 | 950 | 100 |
| 3 | 946.1 | 950 | 100 |
| 3 | 947.1 | 950 | 100 |
| 4 | 1045.4 | 1050 | 100 |
| 4 | 1045.4 | 1050 | 100 |
| 4 | 1045.4 | 1050 | 100 |
| 4 | 1044.9 | 1050 | 100 |
| 4 | 1043.9 | 1050 | 100 |
| 4 | 1044.9 | 1050 | 100 |
| 4 | 1042 | 1050 | 100 |
| 4 | 1042 | 1050 | 100 |
| 4 | 1042 | 1050 | 100 |
| 4 | 1045.6 | 1050 | 100 |
| 4 | 1046.6 | 1050 | 100 |
| 4 | 1047.6 | 1050 | 100 |
| 5 | 1141.9 | 1150 | 100 |
| 5 | 1141.3 | 1150 | 100 |
| 5 | 1142.9 | 1150 | 100 |
| 5 | 1144.3 | 1150 | 100 |
| 5 | 1143.5 | 1150 | 100 |
| 5 | 1140.9 | 1150 | 100 |
| 5 | 1141.9 | 1150 | 100 |
| 5 | 1142.2 | 1150 | 100 |
| 5 | 1142.1 | 1150 | 100 |
| 5 | 1140 | 1150 | 100 |
| 5 | 1140.7 | 1150 | 100 |
| 5 | 1142.7 | 1150 | 100 |
Subiremos los datos al sistema.
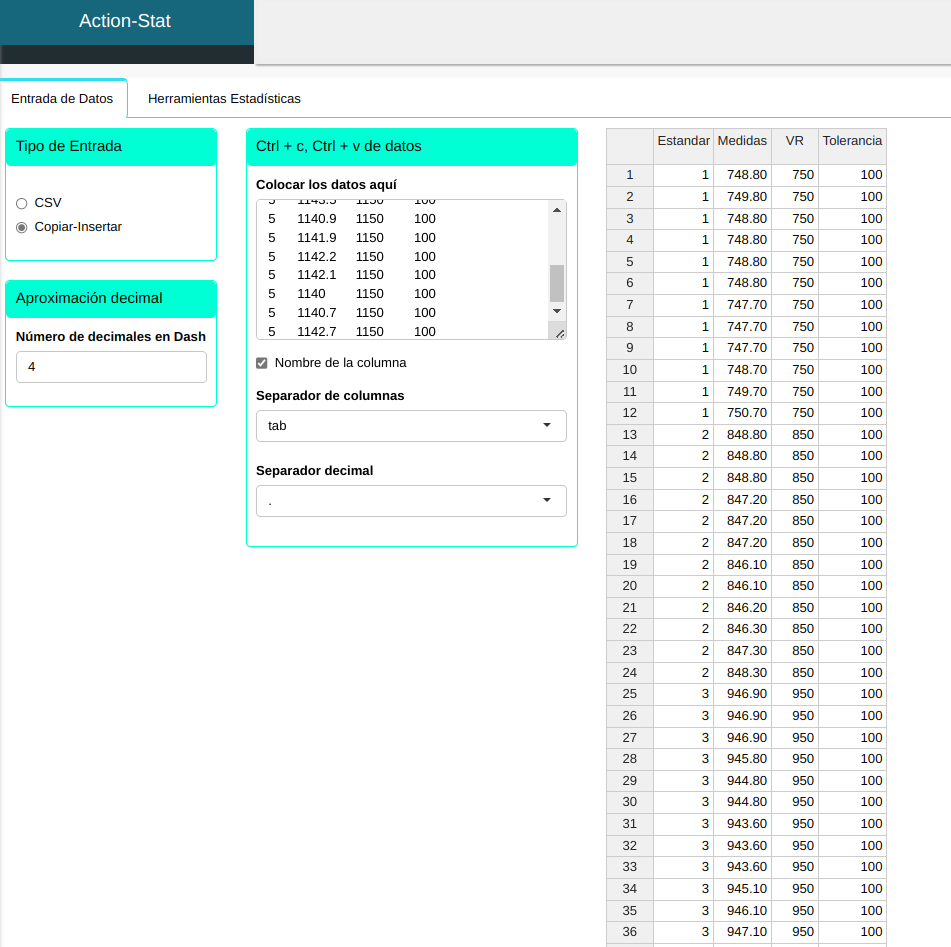
Realizaremos el análisis y ajustamos conforme la figura abajo.

En seguida, haga un clic en calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.
Los resultados son:
Resultado del Análisis
| ANÁLISIS DE LINEALIDAD |
Pruebas de coeficiente de regresión lineal
| Estimación | Desviación estándar | Estad. t | P-valor | |
|---|---|---|---|---|
| (Intercepto) | 11.161 | 1.167 | 9.567 | 0 |
| Pendiente | -0.016 | 0.001 | -13.433 | 0 |
Medida descriptiva de calidad de ajuste
| $R^2$ | $R^2$ Ajustado | Estadística t |
|---|---|---|
| 0.757 | 0.753 | 180.456 |
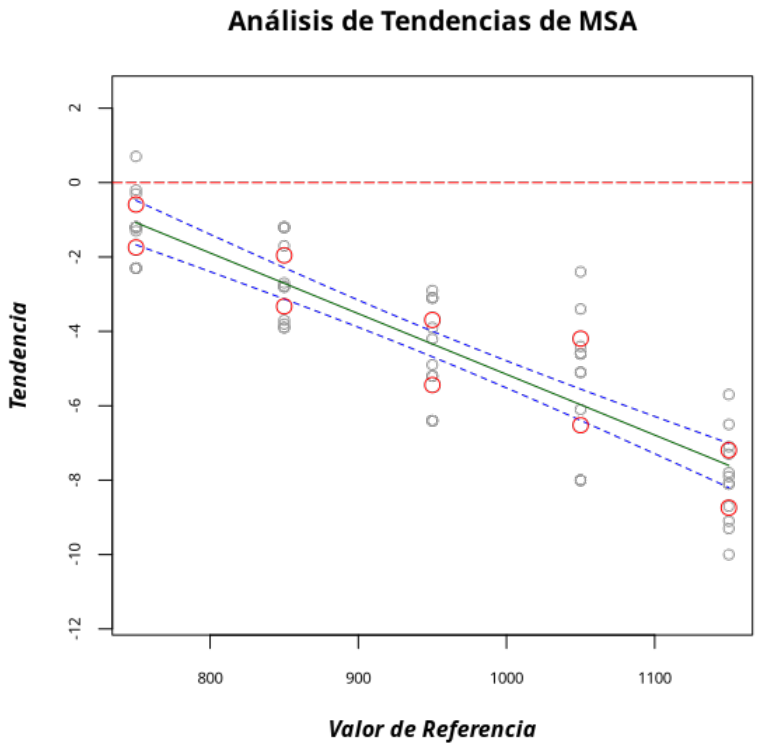
| Análisis de tendencias de MSA |
ANÁLISIS DE TENDENCIAS - Prueba t
| Valor de referencia | Media | Tendencia | Estad. t | P-valor | Límite inferior | Límite superior | VE % | Desviación Estándar |
|---|---|---|---|---|---|---|---|---|
| 750 | 748.833 | -1.167 | -4.456 | 0.001 | -1.743 | -0. | 590 | |
| 850 | 847.358 | -2.642 | -8.474 | 0.000 | -3.328 | -1.956 | 6.480 | 1.080 |
| 950 | 945.433 | -4.567 | -11.502 | 0.000 | -5.441 | -3.693 | 8.252 | 1.375 |
| 1050 | 1044.642 | -5.358 | -10.142 | 0.000 | -6.521 | -4.195 | 10.982 | 1.830 |
| 1150 | 1142.033 | -7.967 | -22.680 | 0.000 | -8.740 | -7.194 | 7.301 | 1.217 |
| Tendencias Medias | ||
| $\qquad \quad$-4.34 |
Ejemplo 2:
El ingeniero de sistemas de medición estaba interesado en determinar la linealidad de un sistema de medición. Para determinar el valor de referencia, se miden 15 veces en el laboratorio de medición cinco elementos estándar que cubren todo el rango de variación del proceso. En este caso, el metrólogo utilizó un instrumento de medición con mejor resolución que el instrumento utilizado normalmente. Luego de determinar el valor de referencia, un evaluador realizó 12 mediciones de cada pieza patrón. Los valores se resumen en la siguiente tabla. Aquí tenemos g=5 (número de piezas) y m=12 (lecturas en cada pieza).
| Piezas | Medidas | VR | Historia |
|---|---|---|---|
| 1 | 2.7 | 2 | 0.744067 |
| 2 | 2.5 | 2 | 0.744067 |
| 3 | 2.4 | 2 | 0.744067 |
| 4 | 2.5 | 2 | 0.744067 |
| 5 | 2.7 | 2 | 0.744067 |
| 6 | 2.3 | 2 | 0.744067 |
| 7 | 2.5 | 2 | 0.744067 |
| 8 | 2.5 | 2 | 0.744067 |
| 9 | 2.4 | 2 | 0.744067 |
| 10 | 2.4 | 2 | 0.744067 |
| 11 | 2.6 | 2 | 0.744067 |
| 12 | 2.4 | 2 | 0.744067 |
| 1 | 5.1 | 4 | 2.684806 |
| 2 | 3.9 | 4 | 2.684806 |
| 3 | 4.2 | 4 | 2.684806 |
| 4 | 5 | 4 | 2.684806 |
| 5 | 3.8 | 4 | 2.684806 |
| 6 | 3.9 | 4 | 2.684806 |
| 7 | 3.9 | 4 | 2.684806 |
| 8 | 3.9 | 4 | 2.684806 |
| 9 | 3.9 | 4 | 2.684806 |
| 10 | 4 | 4 | 2.684806 |
| 11 | 4.1 | 4 | 2.684806 |
| 12 | 3.8 | 4 | 2.684806 |
| 1 | 5.8 | 6 | 1.175894 |
| 2 | 5.7 | 6 | 1.175894 |
| 3 | 5.9 | 6 | 1.175894 |
| 4 | 5.9 | 6 | 1.175894 |
| 5 | 6 | 6 | 1.175894 |
| 6 | 6.1 | 6 | 1.175894 |
| 7 | 6 | 6 | 1.175894 |
| 8 | 6.1 | 6 | 1.175894 |
| 9 | 6.4 | 6 | 1.175894 |
| 10 | 6.3 | 6 | 1.175894 |
| 11 | 6 | 6 | 1.175894 |
| 12 | 6.1 | 6 | 1.175894 |
| 1 | 7.6 | 8 | 0.597723 |
| 2 | 7.7 | 8 | 0.597723 |
| 3 | 7.8 | 8 | 0.597723 |
| 4 | 7.7 | 8 | 0.597723 |
| 5 | 7.8 | 8 | 0.597723 |
| 6 | 7.8 | 8 | 0.597723 |
| 7 | 7.8 | 8 | 0.597723 |
| 8 | 7.7 | 8 | 0.597723 |
| 9 | 7.8 | 8 | 0.597723 |
| 10 | 7.5 | 8 | 0.597723 |
| 11 | 7.6 | 8 | 0.597723 |
| 12 | 7.7 | 8 | 0.597723 |
| 1 | 9.1 | 10 | 0.880083 |
| 2 | 9.3 | 10 | 0.880083 |
| 3 | 9.5 | 10 | 0.880083 |
| 4 | 9.3 | 10 | 0.880083 |
| 5 | 9.4 | 10 | 0.880083 |
| 6 | 9.5 | 10 | 0.880083 |
| 7 | 9.5 | 10 | 0.880083 |
| 8 | 9.5 | 10 | 0.880083 |
| 9 | 9.6 | 10 | 0.880083 |
| 10 | 9.2 | 10 | 0.880083 |
| 11 | 9.3 | 10 | 0.880083 |
| 12 | 9.4 | 10 | 0.880083 |
Subiremos los datos al sistema.
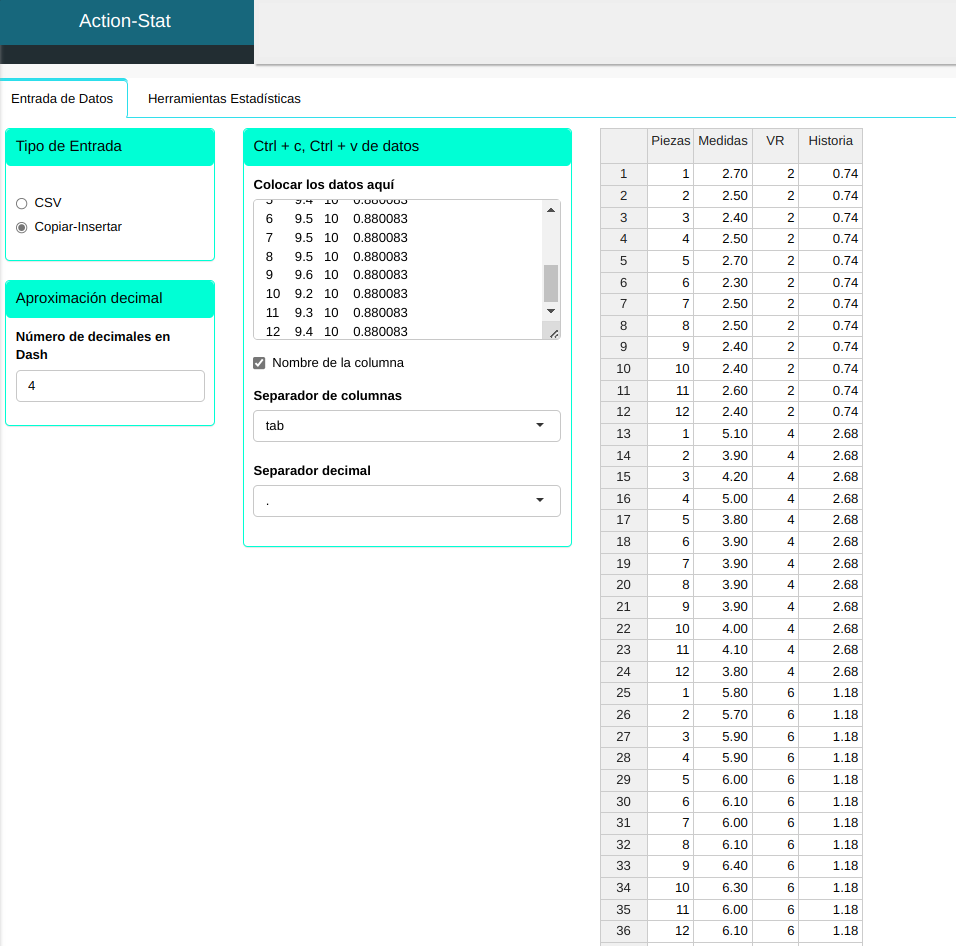
Haremos el análisis y ajustamos conforme la figura abajo.

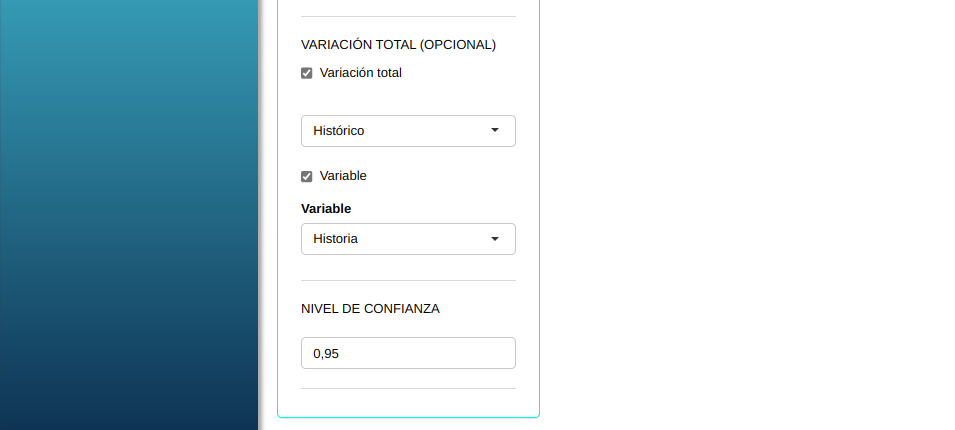
Damos un clic en Calcular y obtenemos los resultados. Los resultados también puden ser descargados en un archivo Word.
Los resultados son:
Resultado del Análisis
| ANÁLISIS DE LINEALIDAD |
Pruebas de coeficiente de regresión lineal
| Estimativa | Desviación estándar | Estad. t | P-valor | |
|---|---|---|---|---|
| (Intercepto) | 0.737 | 0.073 | 10.158 | 0 |
| Coeficiente angular | -0.132 | 0.011 | -12.043 | 0 |
Medida descriptiva de la calidad del ajuste
| $R^2$ | $R^2$ Ajustado | Estadística t |
|---|---|---|
| 0.714 | 0.709 | 145.023 |
| Análisis de tendencias de MSA |
ANÁLISIS DE TENDENCIAS - Prueba t
| Valor de referencia | Media | Tendencia | Estadístico t | P-valor | Límite inferior | Límite superior | VE % | Desviación estándar |
|---|---|---|---|---|---|---|---|---|
| 2 | 2.492 | 0.492 | 13.734 | 0 | 0.413 | 0.57 | 16.666 | 0.124 |
| 4 | 4.125 | 0.125 | 0.968 | 0.354 | -0.159 | 0.409 | 16.667 | 0.447 |
| 6 | 6.025 | 0.025 | 0.442 | 0.667 | -0.1 | 0.15 | 16.667 | 0.196 |
| 8 | 7.708 | -0.292 | -10.142 | 0 | -0.355 | -0.228 | 16.667 | 0.1 |
| 10 | 9.383 | -0.617 | -14.564 | 0 | -0.71 | -0.523 | 16.666 | 0.147 |
| Madias de las Tendencias | ||
| $\qquad \quad$-0.053 |
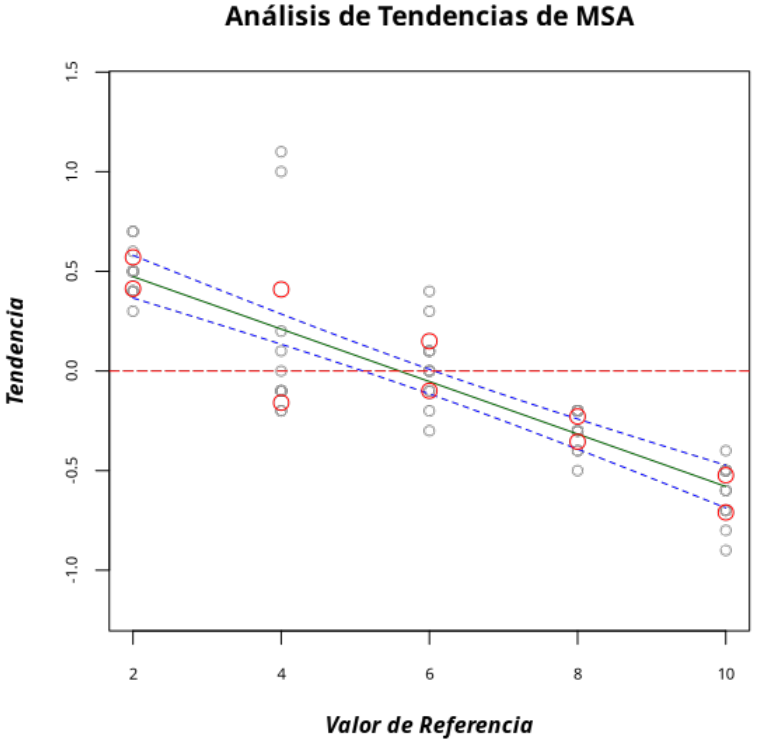
La tendencia se considera significativa en el nivel 0.05 para valores de referencia 2.8 y 10, ya que 0 no está entre los límites de confianza.
La linealidad también se considera significativa en el nivel 0.05, ya que el P-valor es inferior a 0.05, lo que también se puede ver en el gráfico de tendencia.
Ejemplo 3:
Evaluamos la tendencia de un sistema de medición para medir la altura de un reproductor de MP3. Esta altura se mide con un altímetro. Un reproductor de MP3 fue seleccionado (próximo de su valor nominal) y su valor referencia se estableció con un sistema de medición de coordenadas, donde VR = 89.73 mm y tenemos una tolerancia de 0.7 mm. A continuación, se midió el mismo reproductor de " MP3 Player" 12 veces con el sistema de medición bajo análisis.
| Muestra | Medidas |
|---|---|
| 1 | 89.77 |
| 2 | 89.79 |
| 3 | 89.77 |
| 4 | 89.78 |
| 5 | 89.74 |
| 6 | 89.72 |
| 7 | 89.72 |
| 8 | 89.75 |
| 9 | 89.74 |
| 10 | 89.77 |
| 11 | 89.78 |
| 12 | 89.74 |
Subiremos los datos al sistema.
Para realizar el análisis ajustamos conforme la figura abajo.
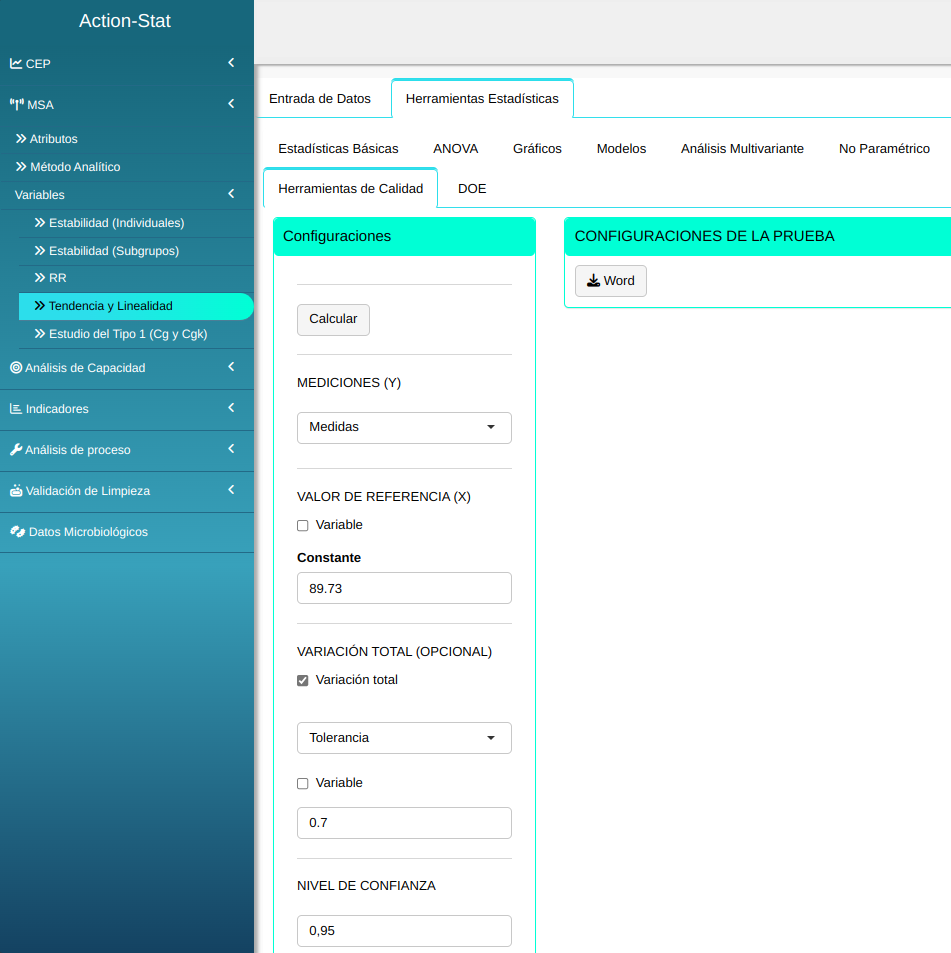
Damos un clic en Calcular y obtenemos los resultados. Los resultados también puden ser descargados en un archivo Word.
Los resultados son:
ANÁLISIS DE TENDENCIAS - Prueba t
| V1 | |
|---|---|
| Valor de referencia | 89.730 |
| Media | 89.756 |
| Tendencia | 0.026 |
| Estadística t | 3.742 |
| P-valor | 0.003 |
| Límite inferior | 0.011 |
| Límite superior | 0.041 |
| VE % | 20.499 |
| Desviación Estándar | 0.024 |
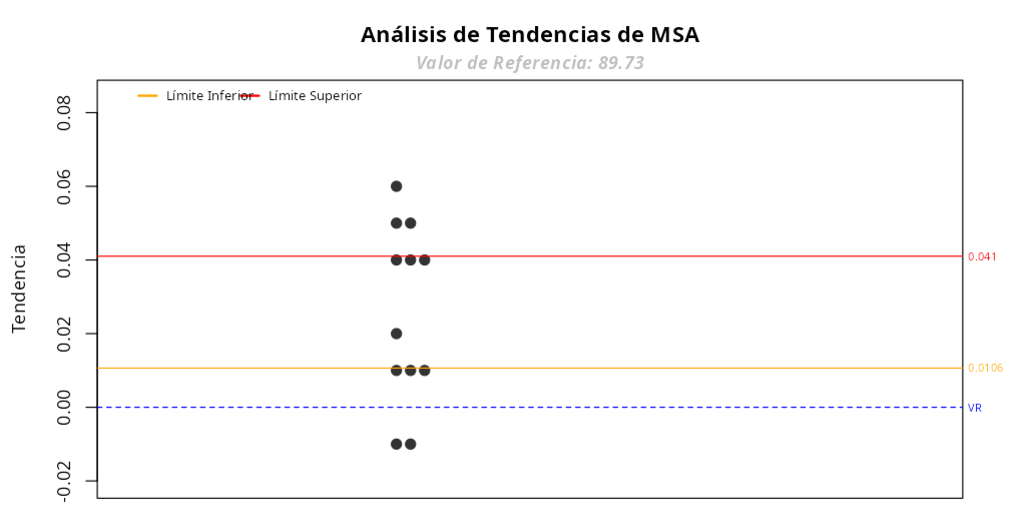
La tendencia se considera significativa en el nivel 0.95, ya que 0 no se encuentra entre los límites de confianza.
El gráfico de tendencias también muestra que muchos puntos tienen una tendencia fuera de estos límites.
Ejemplo 4:
Un ingeniero está evaluando un nuevo sistema de medición para monitorear un proceso. Un análisis del sistema de medición indicó que no debería Puede haber preocupaciones sobre la linealidad, ya que el rango de interés es pequeño. Se eligió una sola pieza de tal manera que se acercara al valor nominal de los procesos. La pieza fue medida mediante un sistema de medición sofisticado para determinar su valor de referencia (valor de referencia = 6). Luego, un operador midió la pieza 15 veces y el valor de la variabilidad total del proceso es 2.5 y este valor se utilizará para validar la repetibilidad del sistema de medición.
| Ensayos | Mediciones |
|---|---|
| 1 | 5.8 |
| 2 | 5.7 |
| 3 | 5.9 |
| 4 | 5.9 |
| 5 | 6 |
| 6 | 6.1 |
| 7 | 6 |
| 8 | 6.1 |
| 9 | 6.4 |
| 10 | 6.3 |
| 11 | 6 |
| 12 | 6.1 |
| 13 | 6.2 |
| 14 | 5.6 |
| 15 | 6 |
Subiremos los datos en el sistema.
Realizaremos el análisis y ajustamos conforme la figura abajo.

Damos un clic en Calcular y obtenemos los resultados. Los resultados también puden ser descargados en un archivo Word.
Los resultados son:
ANÁLISIS DE TENDENCIAS - Prueba t
| V1 | |
|---|---|
| Valor de referencia | 6.000 |
| Media | 6.007 |
| Tendencia | 0.007 |
| estadístico t | 0.122 |
| P-valor | 0.905 |
| Límite inferior | -0.111 |
| Límite superior | 0.124 |
| VE % | 8.481 |
| Desviación estándar | 0.212 |
