5. Histograma

El histograma es una representación gráfica (un gráfico de barras verticales) de la distribución de frecuencia de un conjunto de datos cuantitativos continuo.

Ejemplo:

En una fábrica de autopartes, una arandela selladora estaba causando inconveniente al ensamblar una pieza de un automóvil. Para buscar información, fue decidido medir el espesor de 200 arandelas, cuyos valores fueron:

Espesura de las Arandelas
8.0
10.0
12.0
12.0
11.5
8.0
11.5
9.5
9.5
10.5
13.0
13.5
11.0
14.5
12.0
13.0
11.0
10.5
9.5
11.5
12.5
10.5
10.5
12.5
9.0
13.0
11.5
14.5
13.5
12.5
10.0
10.5
8.0
13.0
7.0
8.0
7.0
7.0
9.5
11.5
12.5
8.0
13.5
15.5
9.5
15.0
10.0
10.0
9.0
14.5
11.0
10.5
11.5
8.5
8.0
10.0
7.5
10.0
12.5
8.0
14.0
15.0
11.5
13.5
11.5
9.5
12.5
5.0
8.0
13.0
8.5
7.5
10.0
11.0
13.5
9.0
15.5
12.5
7.0
10.5
13.5
9.0
12.0
12.5
12.5
12.5
9.0
13.5
12.5
12.5
10.5
8.0
8.5
13.5
13.0
13.0
13.0
9.5
9.5
14.5
12.0
13.0
15.5
17.0
14.0
15.0
13.0
7.5
12.0
12.0
7.0
12.5
10.5
8.5
6.0
15.0
15.5
10.0
12.0
8.5
14.0
11.0
14.0
8.0
11.5
13.5
11.5
11.0
9.5
13.0
10.0
10.5
12.0
11.0
10.0
10.0
11.5
10.0
10.0
10.0
12.0
10.0
7.5
11.0
13.0
12.0
16.0
9.0
10.0
8.5
12.0
14.5
10.5
11.0
10.0
13.5
10.5
12.0
10.0
12.5
10.0
14.0
11.5
11.5
13.0
11.0
10.5
10.5
7.5
10.5
12.0
12.0
11.0
10.0
12.0
11.5
9.5
8.5
8.5
12.5
14.5
11.0
11.0
17.0
15.0
11.0
9.0
14.0
10.5
10.5
10.5
8.0
10.5
12.5
14.5
7.5
9.5
10.0
12.0
11.0

Subiremos los datos al sistema.

Haremos un Histograma. Configuramos conforme la figura abajo.

En seguida, haga un clic en calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.

Los resultados son:

Tabla de frecuencia

Clase	Frec.	Frec. Rel.	Frec. Perc.	Frec. Acum.	Densidades	Punto medio
[5; 6.2)	2	0.01	1.0	1.0	0.008	5.6
[6.2; 7.4)	5	0.02	2.5	3.5	0.021	6.8
[7.4; 8.6)	25	0.12	12.5	16.0	0.104	8.0
[8.6; 9.8)	18	0.09	9.0	25.0	0.075	9.2
[9.8; 11)	40	0.20	20.0	45.0	0.167	10.4
[11; 12,2)	46	0.23	23.0	68.0	0.192	11.6
[12.2; 13.4)	29	0.14	14.5	82.5	0.121	12.8
[13.4; 14.6)	23	0.12	11.5	94.0	0.096	14.0
[14.6; 15.8)	9	0.04	4.5	98.5	0.038	15.2
[15.8; 17)	3	0.02	1.5	100.0	0.012	16.4

Resumen descriptivo

	Valores
Mínimo	5.000
1er cuartil	9.625
Mediana	11.000
Media	11.152
3er cuartil	12.500
Máximo	17.000
Desviación estándar	2.249

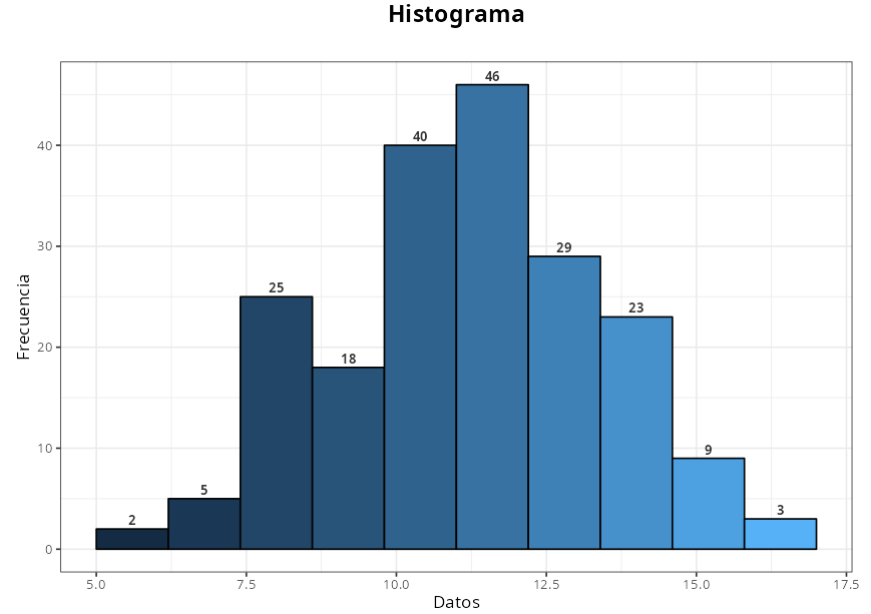
En el histograma vemos que la espesura de las arandelas se ajustan, aproximadamente, a una distribución normal, con las medidas concentradas próxima a la media (entre 9 y 11 mm).