8. Intervalo de Confianza para las Media

Una simple estimación de la media no da idea de lo próximo o lejos que está del valor real, o mejor dicho, de la precisión del resultado. Por lo tanto, un método habitual para especificar esta precisión es determinar un intervalo de confianza para el parámetro poblacional.

Ejemplo 1:

Consideremos un conjunto de datos con un factor y varios niveles.

---

Factor	Resistencia
15	7
15	7
15	15
15	11
15	9
20	12
20	17
20	12
20	18
20	18
25	14
25	18
25	18
25	19
25	19
30	19
30	25
30	22
30	19
30	23
35	7
35	10
35	11
35	15
35	11

---

Subiremos los datos al sistema.

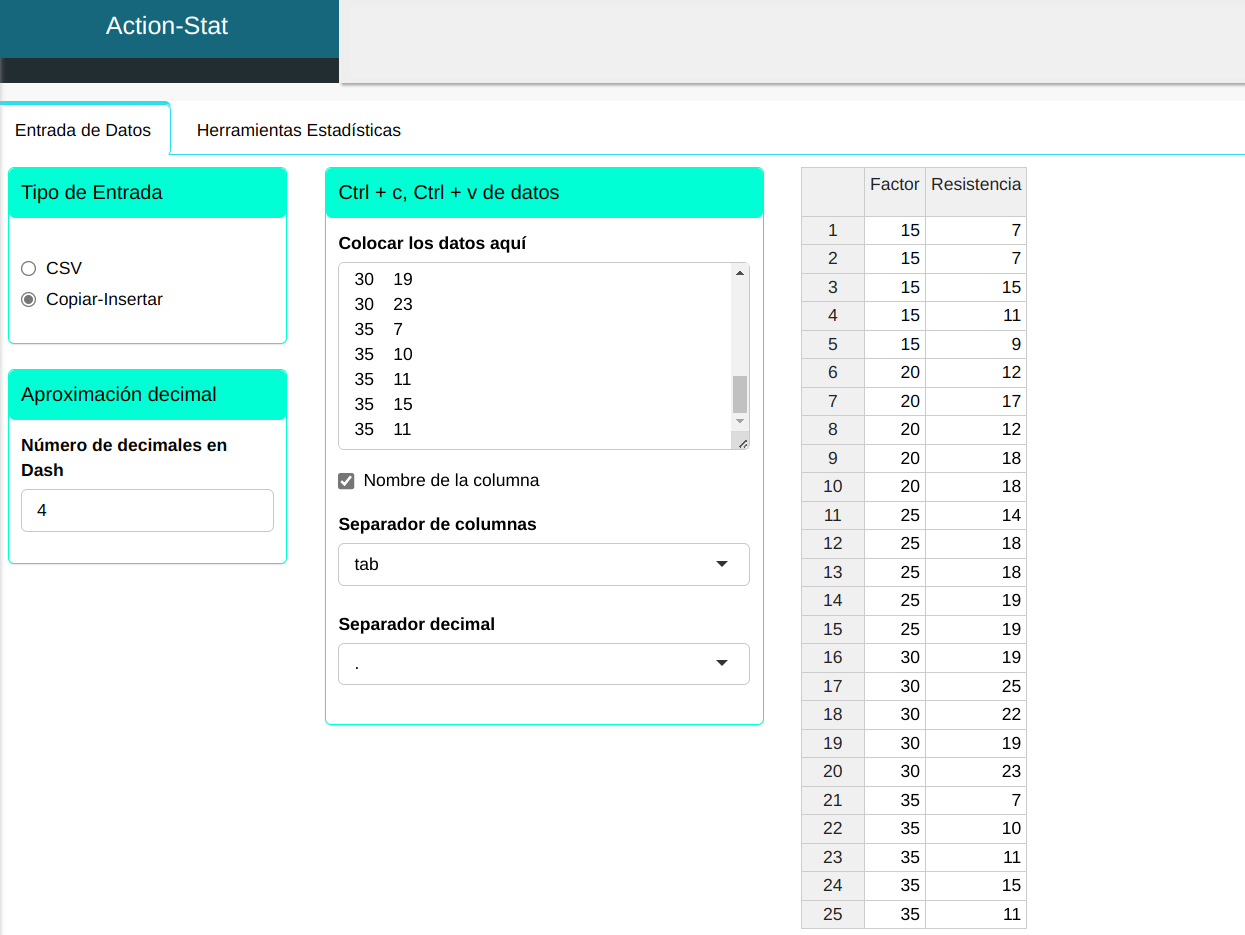
Usaremos la herramienta intervalo de confianza de medias. Configuramos conforme la figura abajo.

En seguida, haga un clic en calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.

Los resultados son:

Intervalo de confianza de las medias

	Promedio	Desviación estándar	Límite inferior	Límite superior
1	9.8	2.839	7.152	12.448
2	15.4	2.839	12.752	18.048
3	17.6	2.839	14.952	20.248
4	21.6	2.839	18.952	24.248
5	10.8	2.839	8.152	13.448

---

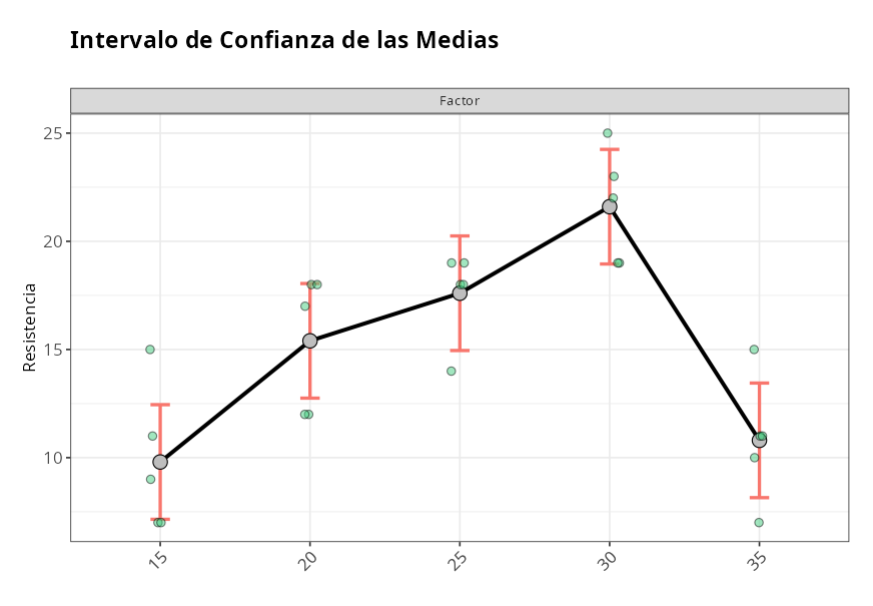
El gráfico y la tabla muestran la media de cada nivel y los respectivos intervalos de confianza. Se observa que los cinco factores difieren en cuanto a su resistencia, ya que el factor 30 presenta resultados relativamente más elevados que los demás.

Ejemplo 2:

Consideremos un conjunto de datos con dos factores (caja de reducción y eje) y varios niveles, como se muestra en la siguiente tabla.

Caja de Reducción	Eje	Ruido
Importado	enrollado	39.6
Nacional	enrollado	42.1
Nacional	Importado	40.9
Nacional	Recortada	38.2
Nacional	enrollado	42.00
Importado	Recortada	41.3
Importado	Importado	39.6
Nacional	enrollado	40.3
Nacional	Importado	40.7
Importado	Importado	36.9
Importado	enrollado	40.2
Importado	Recortada	46.8
Importado	Recortada	40.3
Nacional	Recortada	37.4
Nacional	Recortada	37.00
Importado	enrollado	48.40
Importado	Importado	39.90
Nacional	Importado	39.40
Importado	enrollado	40.90
Nacional	enrollado	38.90
Importado	Recortada	40.50
Nacional	Recortada	42.30
Importado	Importado	38.10
Importado	Importado	38.00
Importado	Importado	36.70
Nacional	Recortada	40.5
Nacional	enrollado	38.9
Importado	Importado	37.2
Importado	enrollado	39.9
Nacional	enrollado	43.7
Nacional	Importado	41.4
Nacional	enrollado	41.00
Importado	Recortada	41.3
Nacional	Importado	41.3
Importado	Importado	36.7
Nacional	enrollado	40.1
Nacional	Recortada	41.3
Importado	enrollado	41.00
Nacional	Importado	40.6
Nacional	Recortada	40.4
Nacional	enrollado	40.3
Nacional	Importado	41.3
Importado	Recortada	40.1
Importado	enrollado	42.7
Importado	Recortada	41.6
Nacional	Importado	41.6
Importado	Importado	36.2
Importado	enrollado	41.00
Importado	Recortada	39.9
Importado	enrollado	41.00
Nacional	Recortada	41.3
Nacional	Importado	42.00
Importado	Recortada	39.30
Nacional	Recortada	42.10

Subiremos los datos al sistema.

Usaremos la herramienta Intervalo de confianza medio. Configuramos conforme la figura de abajo.

En seguida, haga un clic en Calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.

Los resultados son:

Intervalo de confianza de las medias

	Media	Desviación estándar	Límite inferior	Límite superior
1	40.1889	2.1172	39.3705	41.0073
2	40.6296	2.1172	39.8112	41.448

---

Intervalo de confianza de las medias

	Media	Desviación estándar	Límite inferior	Límite superior
1	40.6444	2.1172	39.6421	41.6468
2	39.3611	2.1172	38.3588	40.3635
3	41.2222	2.1172	40.2199	42.2246

---

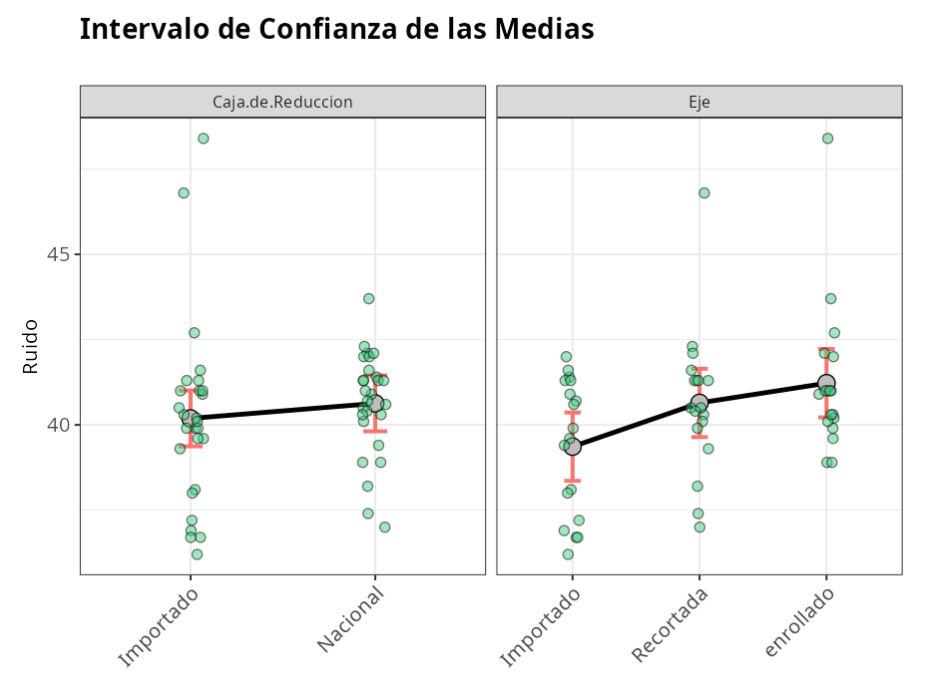
En el gráfico y también en la tabla, tenemos la media de cada nivel y los respectivos intervalos de confianza. Aquí observamos que independientemente de los factores y sus respectivos niveles, el ruido se comporta de forma muy similar, excepto cuando se considera el eje importado, donde el ruido, en promedio, disminuye.