6. ID Plot
Manera de verificar, mediante papel de probabilidad, una distribución que mejor describe la aleatoriedad de un conjunto de datos.
Ejemplo:
Consideramos el conjunto de datos en la siguiente tabla. Vamos a comprobar qué distribución de probabilidad describe mejor este conjunto de datos.
| Medidas |
|---|
| 0.20 |
| 0.16 |
| 0.24 |
| 0.56 |
| 0.34 |
| 0.33 |
| 0.35 |
| 0.20 |
| 0.28 |
| 0.81 |
| 0.30 |
| 1.19 |
| 0.46 |
| 0.12 |
| 0.50 |
| 0.46 |
| 0.69 |
| 0.11 |
| 0.32 |
| 0.28 |
| 0.57 |
| 0.42 |
| 0.91 |
| 0.79 |
| 0.51 |
| 0.67 |
| 0.70 |
| 0.19 |
| 0.22 |
| 0.62 |
| 0.56 |
| 0.96 |
| 0.11 |
| 0.85 |
| 0.37 |
| 0.80 |
| 0.52 |
| 0.17 |
| 0.58 |
| 0.15 |
| 0.20 |
| 0.05 |
| 0.63 |
| 0.53 |
| 0.60 |
| 0.21 |
| 0.29 |
| 0.41 |
| 0.43 |
| 0.75 |
Subiremos los datos al sistema.
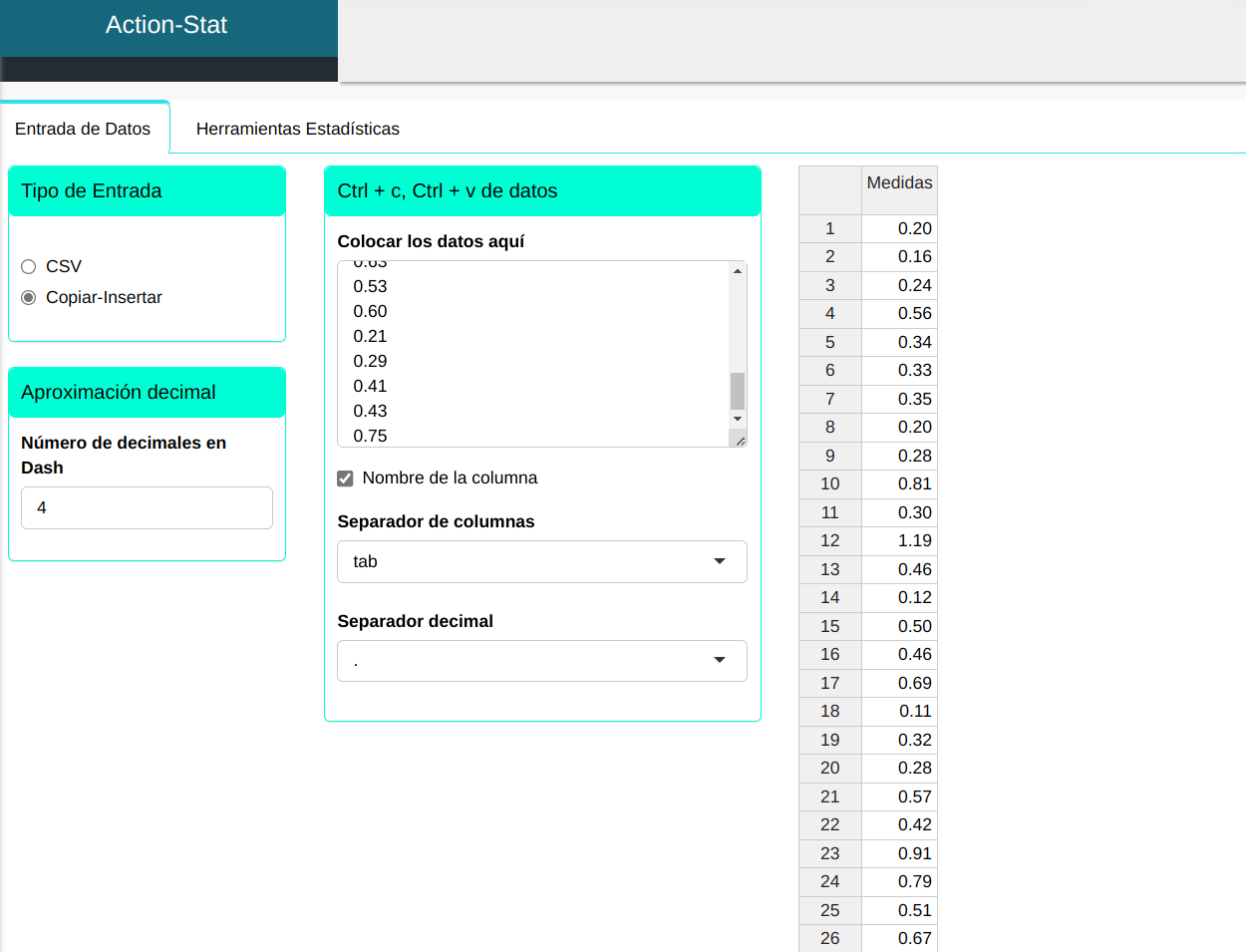
Construiremos el ID Plot. Configuramos conforme la figura de abajo.
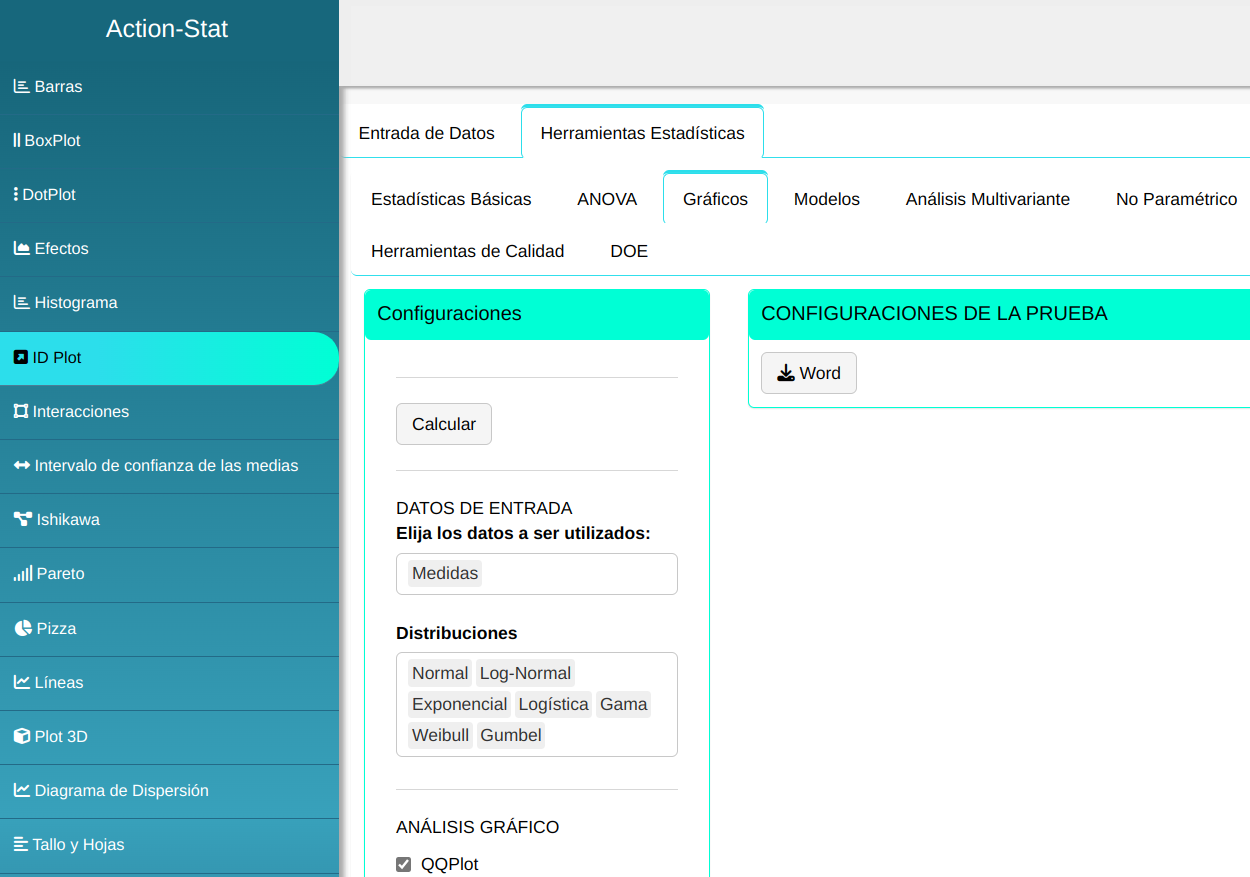
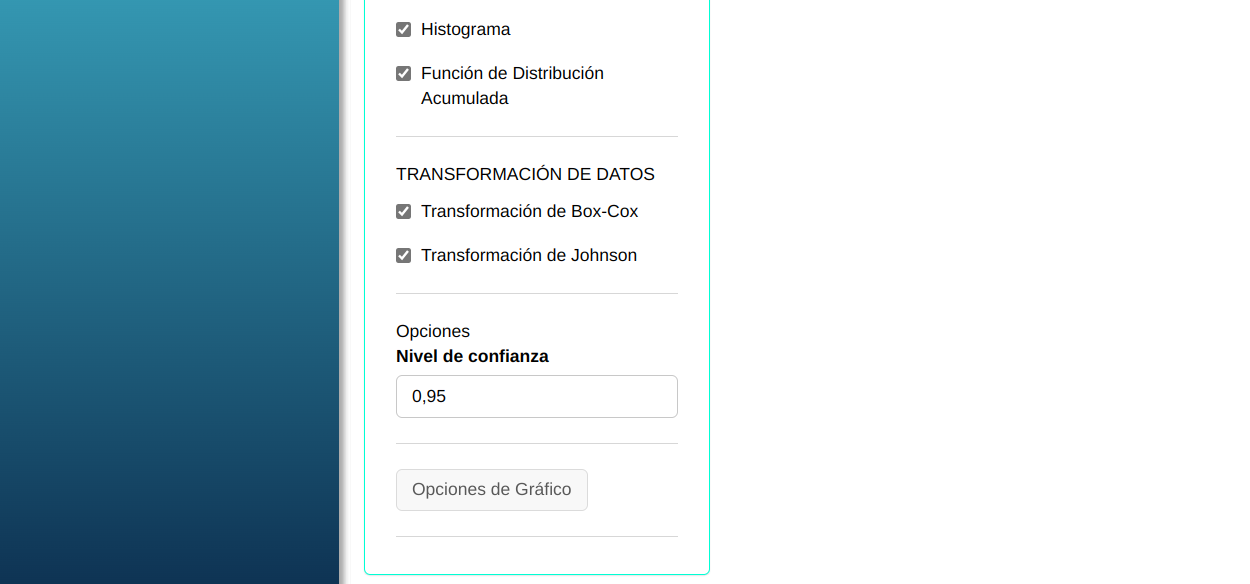
En seguida, haga un clic en calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.

Los resultados son:
Resultado del análisis
| Transformación de Box-Cox |
| Valores | |
|---|---|
| Lambda | 0.429 |
| P-valor (Anderson-Darling) | 0.703 |
Resultado del análisis
| Transformación de Johnson |
Estimativas
| Prueba | |
|---|---|
| Gama | 0.90802942754439 |
| Lambda | 1.36936290670753 |
| Épsilon | 0.0168457063069285 |
| Eta | 0.951739827664239 |
| Familia | SB |
| P-valor (Anderson-Darling) | 0.9422 |
Anderson-Darling
| Distribuciones | Estad. | P-valor | |
|---|---|---|---|
| 1 | Normal($\mu$ = 0.45, $\sigma$ = 0.26) | 0.566 | 0.136 |
| 2 | Log-Normal(log($\mu$) = -0.982398, log($\sigma$) = 0.667801) | 0.589 | 0.118 |
| 1-mle-exp | Exponencial(Tasa = 2,20556) | 3.845 | 0.000 |
| 11 | Logística(Posición = 0.44, Escala = 0.15) | 0.581 | 0.089 |
| 12 | Gamma(Forma = 2.76743, Velocidad = 6.10372) | 0.295 | 0.250 |
| 13 | Weibull(Forma = 1.84755, Escala = 0.511436) | 0.217 | 0.250 |
| 14 | Gumbel(Posición = 0.332819, Escala = 0.207431) | 0.384 | 0.250 |
Cramer-von-Misés
| Distribuciones | Estad. | P-valor |
|---|---|---|
| Normal($\mu$ = 0.45, $\sigma$ = 0.26) | 0.082 | 0.192 |
| Log-Normal(log($\mu$) = -0.982398, log($\sigma$) = 0.667801) | 0.100 | 0.114 |
| Exponencial(Tasa = 2.20556) | 0.678 | 0.000 |
| Logística(Posición = 0.44, Escala = 0.15) | 0.076 | 0.232 |
| Gamma(Forma = 2.76743, Tasa = 6.10372) | 0.051 | 0.497 |
| Weibull(Forma = 1.84755, Escala = 0.511436) | 0.035 | 0.765 |
| Gumbel(Posición = 0.332819, Escala = 0.207431) | 0.065 | 0.329 |
Kolmogorov-Smirnov
| Distribuciones | Estad. | P-valor |
|---|---|---|
| Normal($\mu$ = 0.45, $\sigma$ = 0,26) | 0,095 | 0,313 |
| Log-Normal(log($\mu$) = -0.982398, log($\sigma$) = 0.667801) | 0.108 | 0.158 |
| Exponencial(Tasa = 2.20556) | 0.202 | 0.000 |
| Logística(Posición = 0.44, Escala = 0.15) | 0.082 | 0.550 |
| Gamma(Forma = 2.76743, Tasa = 6.10372) | 0.083 | 0.534 |
| Weibull(Forma = 1.84755, Escala = 0.511436) | 0.070 | 0.778 |
| Gumbel(Posición= 0.332819, Escala = 0.207431) | 0.081 | 0.559 |
Resultado del análisis.
| Análisis Gráfico |
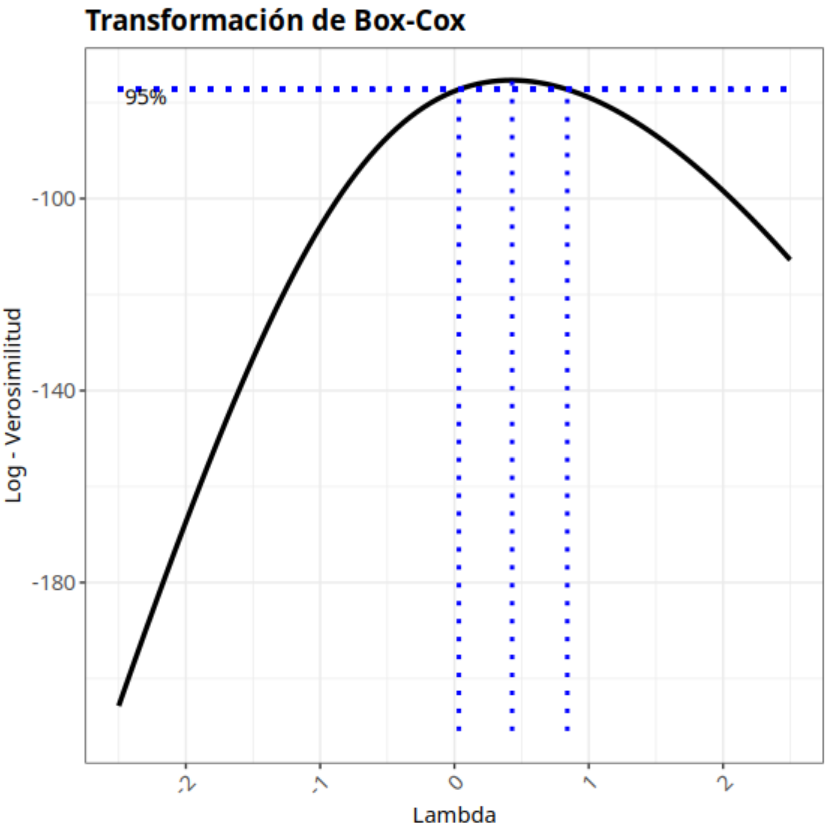
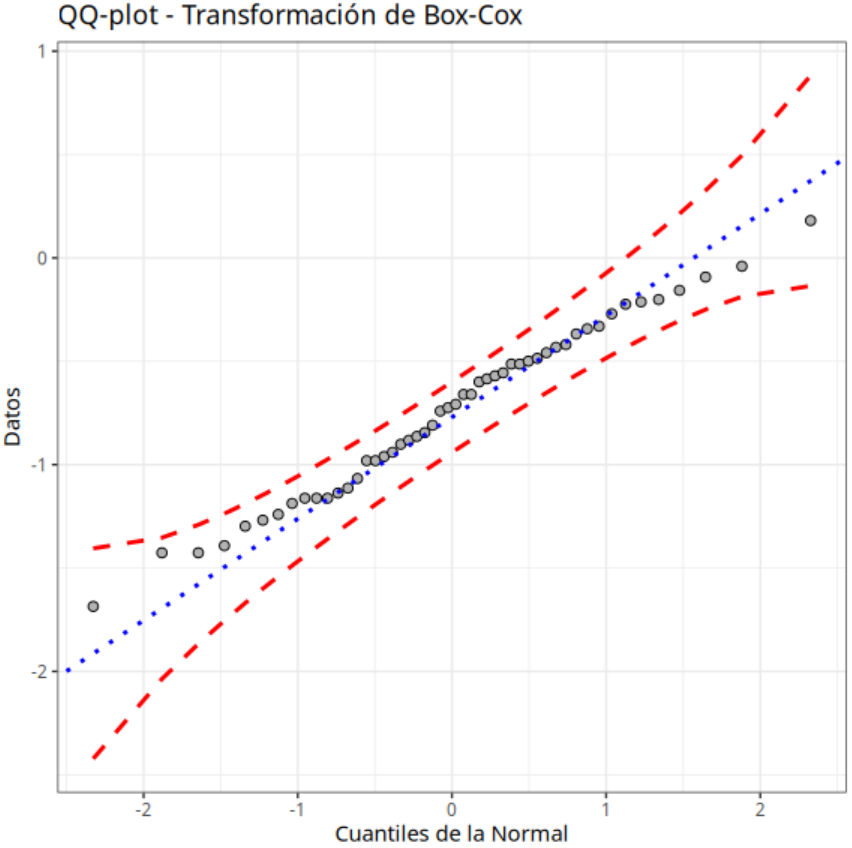
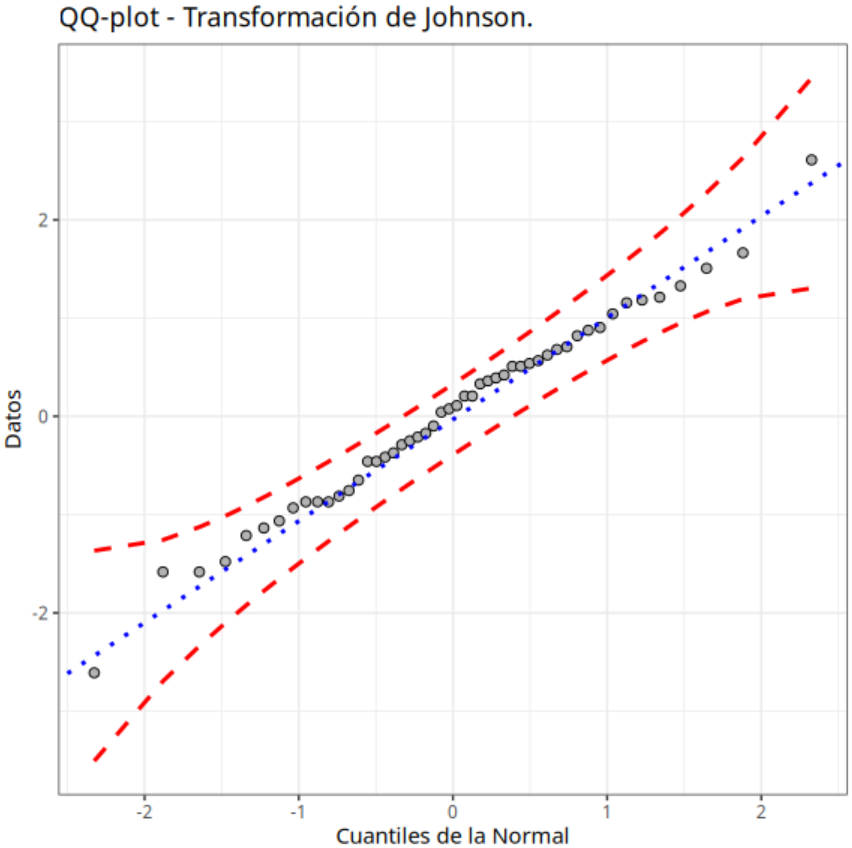
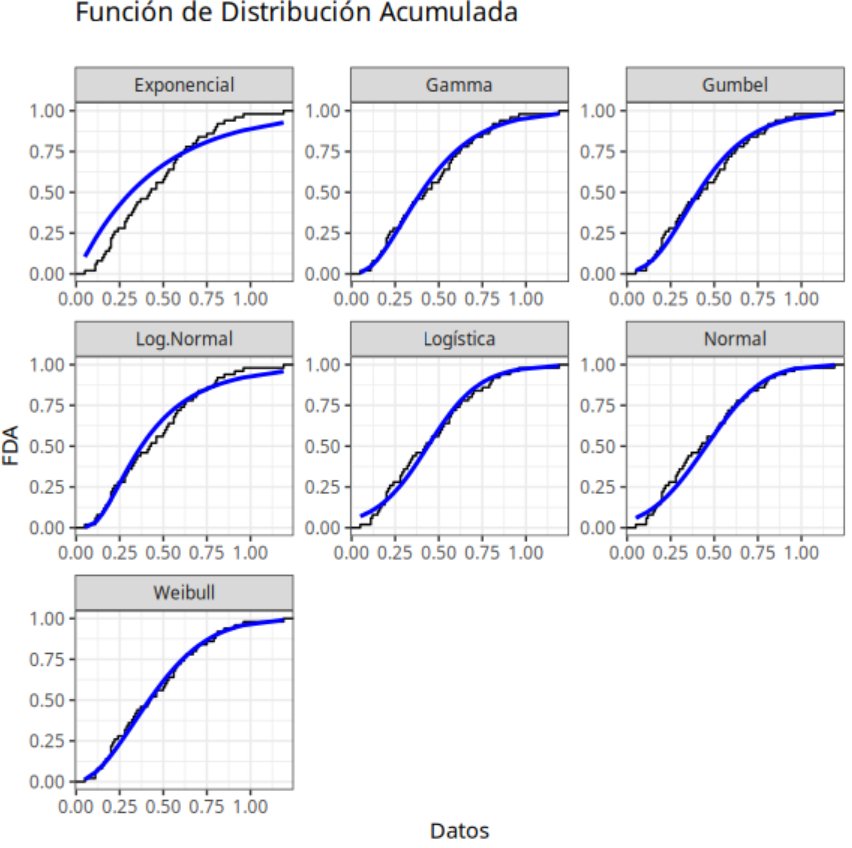
Los datos transformados mediante los métodos de Transformación de Box-Cox y Transformación de Johnson siguen una distribución normal. Este resultado puede confirmarse observando el P-valor asociado a la prueba de Anderson-Darling.
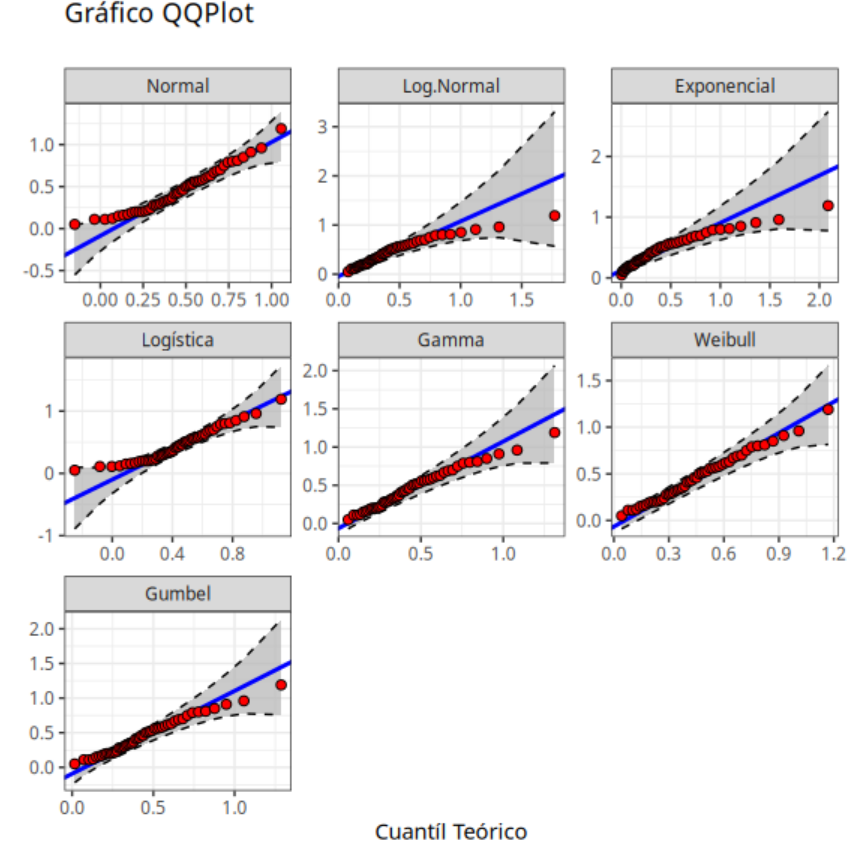
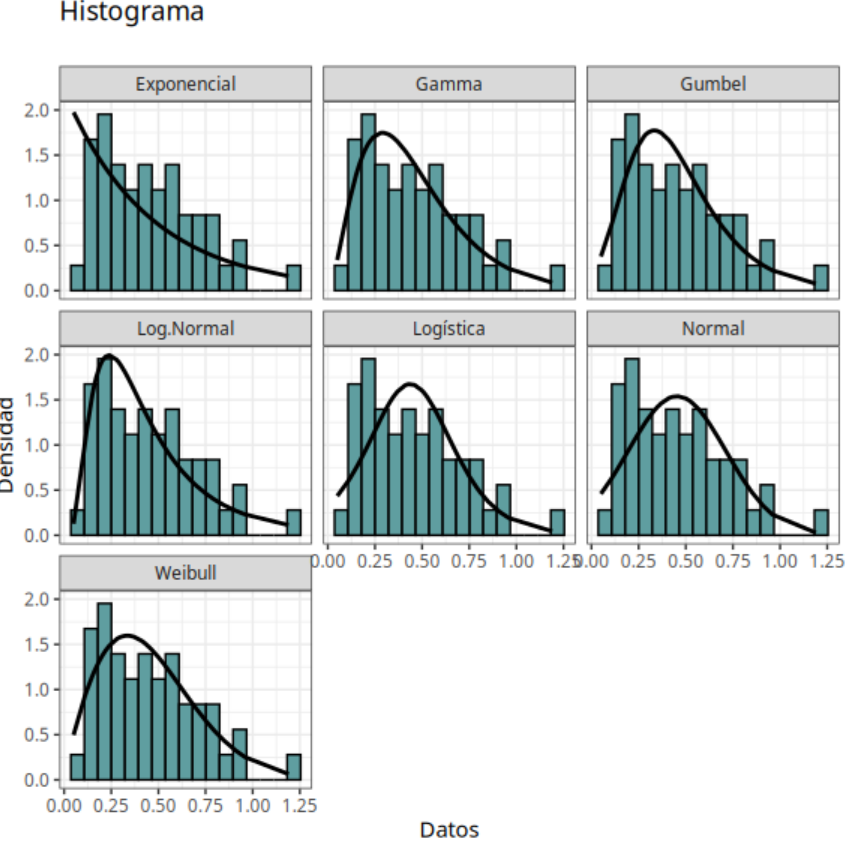
La tabla indica que los datos pueden ser mejor ajustados por todas las distribuciones excepto la distribución exponencial, lo que puede confirmarse cuando comparamos el P-valor de la prueba de Anderson-Darling con el nivel de significancia de 0.05.