3. Modelo Binomial

El modelo de regresión binomial se utiliza cuando la variable de respuesta es cualitativo con dos resultados posibles.

Ejemplo:

Un analista está estudiando el efecto de tiempo de experiencia en programación de computadoras sobre la capacidad de completar una tarea difícil en un tiempo determinado. Se seleccionaron veinticinco programadores para el estudio. La variable predictiva, X, corresponde a meses de experiencia.

Observación:

Tarea (Y) = 1, si la tarea se completó con éxito dentro del tiempo permitido y

Tarea (Y) = 0, si la tarea no se completó con éxito.

MesesExperiencia	Tarea
14	0
29	0
6	0
25	1
18	1
4	0
18	0
12	0
22	1
6	0
30	1
11	0
30	1
5	0
20	1
13	0
9	0
32	1
24	0
13	1
19	0
4	0
28	1
22	1
8	1

---

Subiremos los datos al sistema.

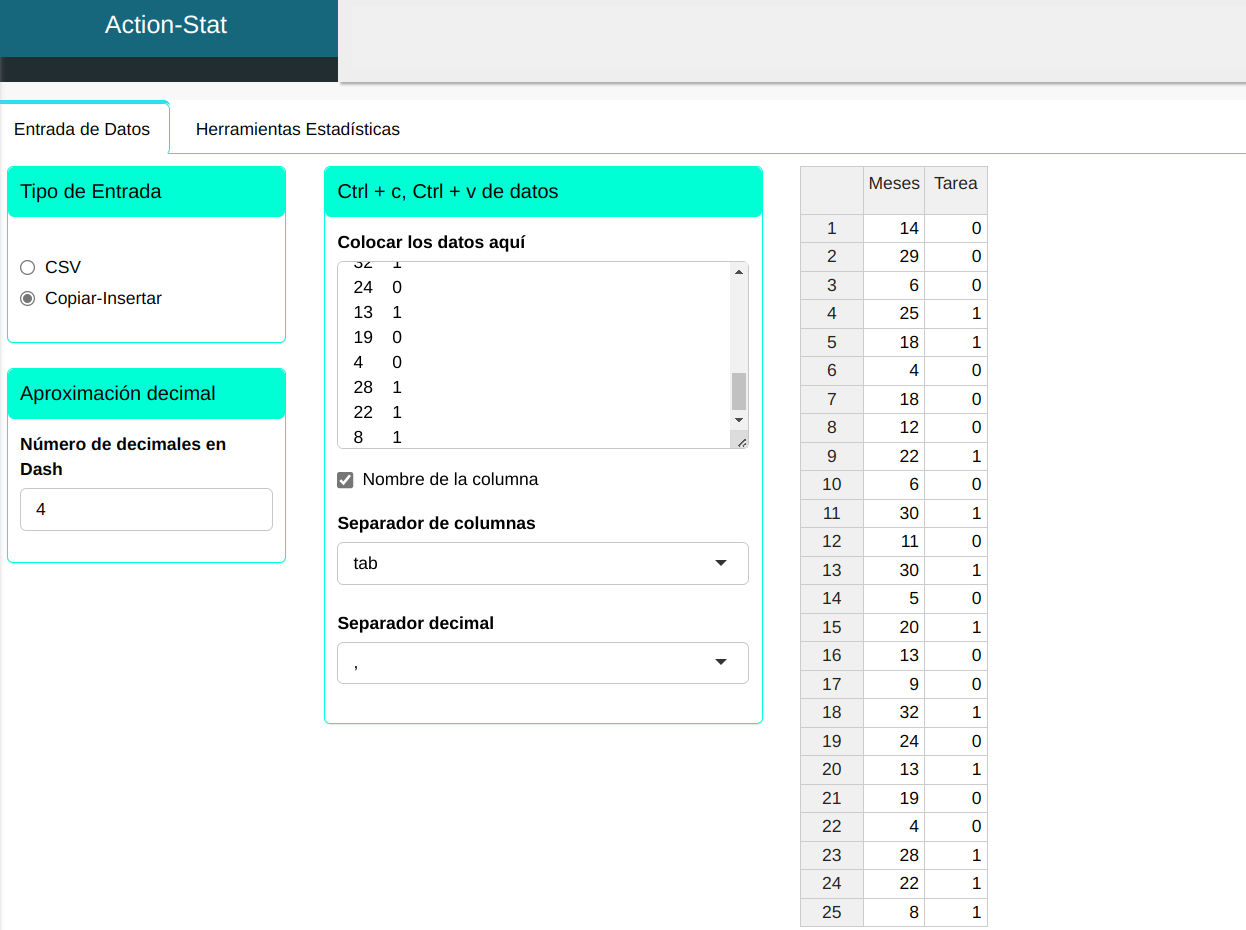
Realizaremos el análisis “Modelo Binomial”, configurando conforme la figura abajo.

En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:

Cuadro de Estimación de coeficientes

	Estimativa	Desviación estándar	Prueba de Wald	P-valor	Límite inferior	Límite superior
Intercepto	-3.0596959	1.25934986	-2.429584	0.0151	-5.52797622	-0.5914155
Meses	0.1614859	0.06498001	2.485163	0.0129	0.03412744	0.2888444

---

Matriz de covarianza

	(Intercepto)	Meses
(Intercepto)	1.5859621	-0.075402604
Meses	-0.0754026	0.004222402

---

Informaciones generales

Información	Valor
Interacción de escore de Fisher	4
Desviación Nula	34.296 con 24 Grados de Libertad
Desviación Residual	25.425 con 23 Grados de Libertad
AIC	29.4245740804509
Parámetro de dispersión	1

---

Resultado del análisis

	Real	V2
Previsto	Tarea=0	Tarea=1
Tarea=0	13	6
Tarea=1	1	5

---

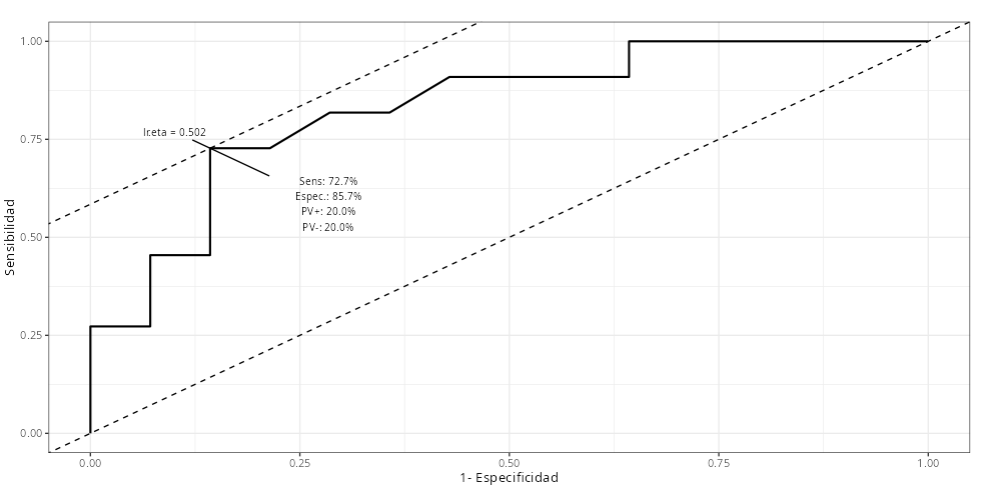
Resumen (Rendimiento)

	Porcentaje (%)
Sensibilidad	45.45455
Especificidad	92.85714
VPP	83.33333
VPN	68.42105
Precisión	72.00000

---

Cuadro de Odds Ratio

Variable	Categorías	Odds Ratio	Límite inferior	Límite superior
Meses		1.1752559100685	1.03471646443219	1.3348840012021

---

Intervalo de Previsión

	Meses	Probabilidad Ajustada	LI	LS	Desviación Estándar
1	14	0.31026237	0.079658965	0.5408658	0.11765696
2	29	0.83526292	0.599589805	1.0709360	0.12024360
3	6	0.10999616	-0.065139980	0.2851323	0.08935681
4	25	0.72660237	0.464020009	0.9891847	0.13397306
5	18	0.46183704	0.223425450	0.7002486	0.12164080
6	4	0.08213002	-0.069291566	0.2335516	0.07725733
7	12	0.24566554	0.020497984	0.4708331	0.11488352
8	22	0.62081158	0.363141740	0.8784814	0.13146662
9	30	0.85629862	0.632385431	1.0802118	0.11424352
10	11	0.21698039	-0.003406564	0.4373674	0.11244439
11	5	0.09515416	-0.068239496	0.2585478	0.08336564
12	20	0.54240353	0.294917361	0.7898897	0.12627078
13	13	0.27680234	0.048333968	0.5052707	0.11656764
14	9	0.16709980	-0.038978483	0.3731781	0.10514391
15	32	0.89166416	0.694547616	1.0887807	0.10057152
16	24	0.69337941	0.430252386	0.9565064	0.13425095
17	19	0.50213414	0.259630105	0.7446382	0.12372882
18	28	0.81182461	0.566052911	1.0575963	0.12539603
19	8	0.14581508	-0.050963101	0.3425933	0.10039887

---

Intervalo de predicción

	Meses	Probabilidad ajustada	LI	LS	Desviación estándar
1	14	0.31026237	0.079658965	0.5408658	0.11765696
2	29	0.83526292	0.599589805	1.0709360	0.12024360
3	6	0.10999616	-0.065139980	0.2851323	0.08935681
4	25	0.72660237	0.464020009	0.9891847	0.13397306
5	18	0.46183704	0.223425450	0.7002486	0.12164080
6	4	0.08213002	-0.069291566	0.2335516	0.07725733
7	18	0.46183704	0.223425450	0.7002486	0.12164080
8	12	0.24566554	0.020497984	0.4708331	0.11488352
9	22	0.62081158	0.363141740	0.8784814	0.13146662
10	6	0.10999616	-0.065139980	0.2851323	0.08935681
11	30	0.85629862	0.632385431	1.0802118	0.11424352
12	11	0.21698039	-0.003406564	0.4373674	0.11244439
13	30	0.85629862	0.632385431	1.0802118	0.11424352
14	5	0.09515416	-0.068239496	0.2585478	0.08336564
15	20	0.54240353	0.294917361	0.7898897	0.12627078
16	13	0.27680234	0.048333968	0.5052707	0.11656764
17	9	0.16709980	-0.038978483	0.3731781	0.10514391
18	32	0.89166416	0.694547616	1.0887807	0.10057152
19	24	0.69337941	0.430252386	0.9565064	0.13425095
20	13	0.27680234	0.048333968	0.5052707	0.11656764
21	19	0.50213414	0.259630105	0.7446382	0.12372882
22	4	0.08213002	-0.069291566	0.2335516	0.07725733
23	28	0.81182461	0.566052911	1.0575963	0.12539603
24	22	0.62081158	0.363141740	0.8784814	0.13146662
25	8	0.14581508	-0.050963101	0.3425933	0.10039887

---

Prueba de ratio de verosimilitud (TRV)

Variables probadas	Estadísticas de prueba	Grados de libertad	Valor P
Meses	8.871916	1	0.002895911

---

Prueba de Hosmer y Lemeshow

	Estadística de prueba	Grados de libertad	P-valor	Número de grupos
tabHosmer	0.8636609	1	0.3527162	3
X	0.1032996	2	0.9496614	4
X.1	2.1663561	3	0.5386055	5
X.2	1.6652041	4	0.7970282	6
X.3	3.4095112	5	0.6371218	7
X.4	3.1422227	6	0.7907964	8
X.5	6.4255004	7	0.4910340	9
X.6	6.5599688	8	0.5847638	10

---

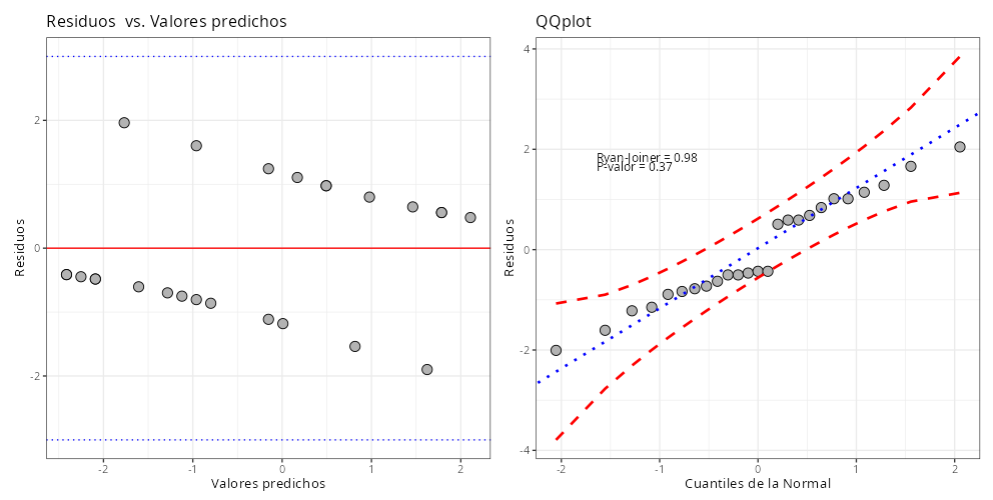
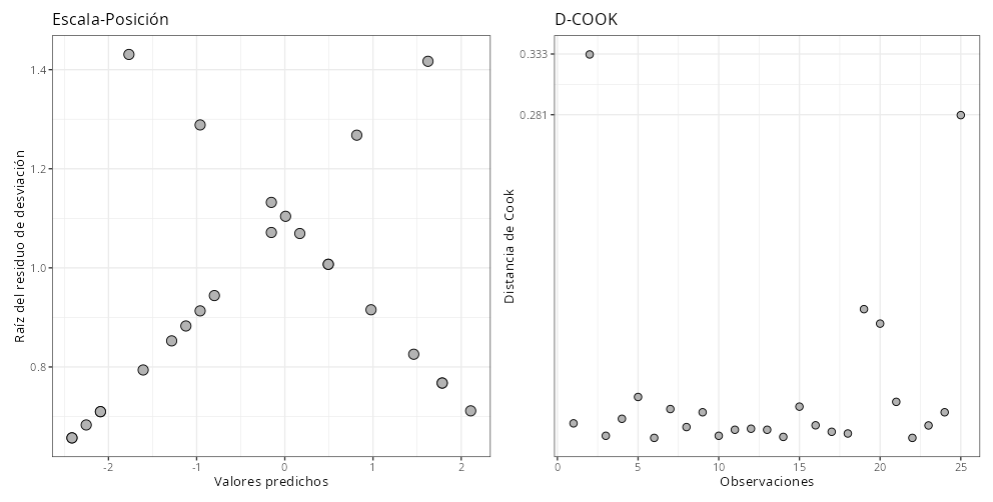
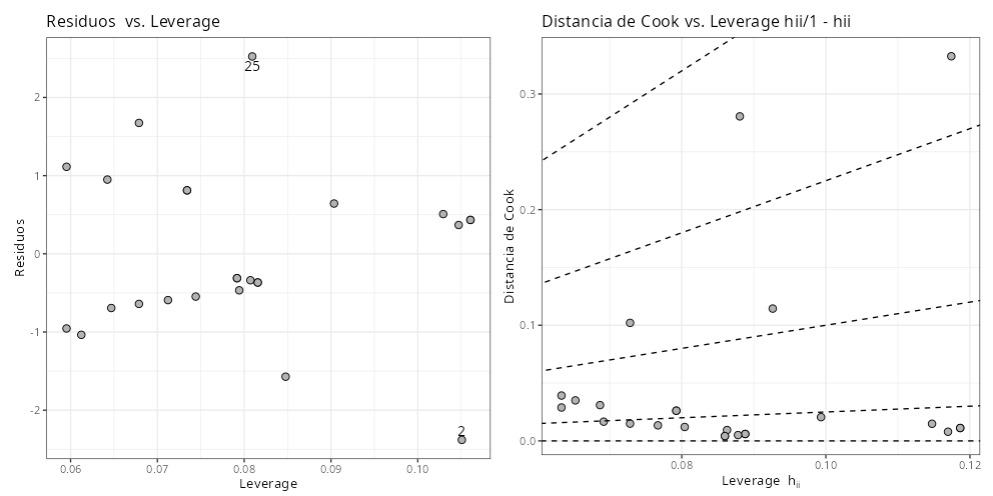
Cuadro de Residuos

	Residuo Desviance	Residual de Pearson	Leverage	Distancia de Cook
1	-0.8912168	-0.6934965	0.06468785	0.016631244
2	-2.0075616	-2.3802536	0.10507761	0.332614571
3	-0.5037418	-0.3668326	0.08156202	0.005975083
4	0.8379723	0.6431504	0.09035322	0.020543100
5	1.2817536	1.1131167	0.05953276	0.039216040
6	-0.4314357	-0.3117255	0.07917694	0.004177699
7	-1.1478806	-0.9552469	0.05953276	0.028881095
8	-0.7791504	-0.5921530	0.07122100	0.013444157
9	1.0143989	0.8119069	0.07342029	0.026116551
10	-0.5037418	-0.3668326	0.08156202	0.005975083
11	0.5891404	0.4332766	0.10606643	0.011137127
12	-0.7269990	-0.5471630	0.07441893	0.012035729
13	0.5891404	0.4332766	0.10606643	0.011137127
14	-0.4664129	-0.3382224	0.08071868	0.005022274
15	1.1434517	0.9495059	0.06423926	0.030945750
16	-0.8338729	-0.6407963	0.06787813	0.014950895
17	-0.6302671	-0.4668354	0.07943296	0.009402490
18	0.5061151	0.3683859	0.10470752	0.007935766
19	-1.6072596	-1.5718845	0.08477399	0.114431488
20	1.6601125	1.6741998	0.06787813	0.102056745
21	-1.2189489	-1.0365150	0.06123640	0.035040847
22	-0.4314357	-0.3117255	0.07917694	0.004177699
23	0.6817493	0.5083200	0.10293029	0.014823864
24	1.0143989	0.8119069	0.07342029	0.026116551
25	2.0469291	2.5246445	0.08092914	0.280625042

---