2. Prueba de Friedman
La Prueba de Friedman es una prueba no paramétrica utilizada como alternativa a la prueba en bloques aleatorizados ANOVA regular, cuando no se puede asegurar los presupuestos de normalidad o cuando las variaciones entre factores son diferentes.
Ejemplo:
En una evaluación del desempeño de un vehículo. seis conductores evaluaron tres carros (A, B y C) en un estudio aleatorio. El objetivo del la investigación es evaluar el rendimiento de los vehículos assumiendo que la marca del vehículo no influye en las calificaciones. En el cuadro, tenemos las clasificaciones de cada carro, según cada conductor, en una escala del 1 al 10.
| Carro | Conductor | Respuesta |
|---|---|---|
| A | 1 | 7 |
| A | 2 | 6 |
| A | 3 | 6 |
| A | 4 | 7 |
| A | 5 | 7 |
| A | 6 | 8 |
| B | 1 | 8 |
| B | 2 | 10 |
| B | 3 | 8 |
| B | 4 | 9 |
| B | 5 | 10 |
| B | 6 | 8 |
| C | 1 | 9 |
| C | 2 | 7 |
| C | 3 | 8 |
| C | 4 | 8 |
| C | 5 | 9 |
| C | 6 | 9 |
Subiremos los datos al sistema.
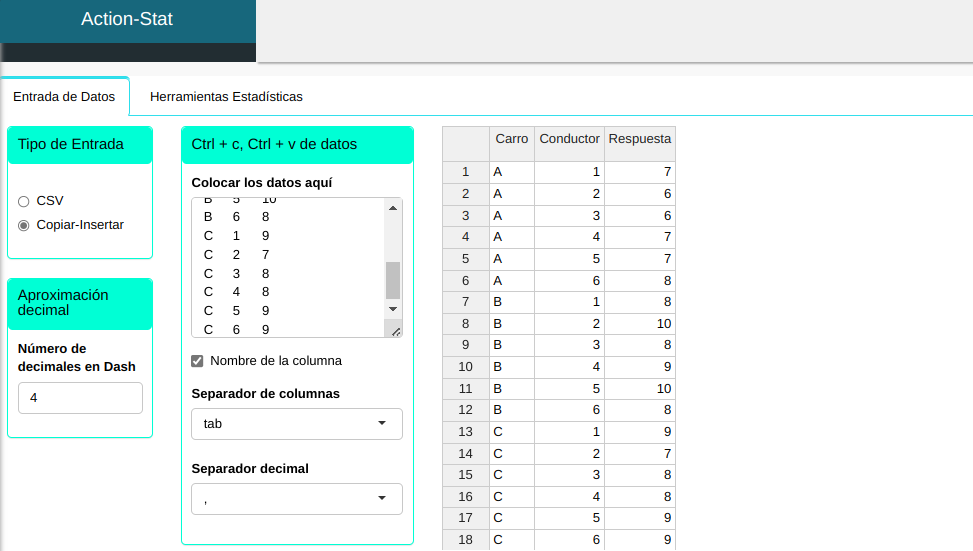
La prueba de Friedman se realizará utilizando la configuración que se muestra en la siguiente figura.
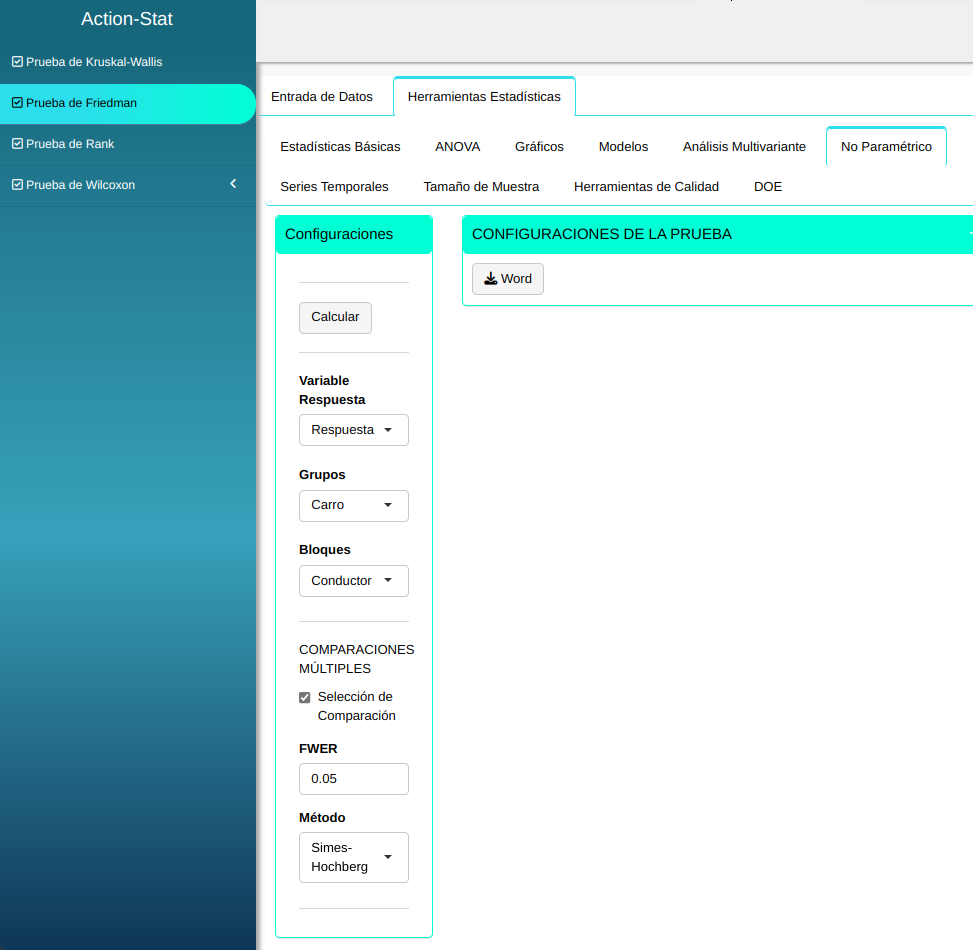
En seguida, haga un clic en calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.
Los resultados son:
Pueba de Friedman
| Valor | |
|---|---|
| Friedman Chi-cuadrado | 8.273 |
| Grados de libertad | 2.000 |
| P-valor | 0.016 |
Cuadro de comparación múltiple - FWER (Simes-Hochberg)
| Diferencia observada | Diferencia crítica | Estadísticas | P-valor | P-valor ajustado | |
|---|---|---|---|---|---|
| A-B | 8.5 | 8.293 | 2.454 | 0.014 | 0.042 |
| A-C | 8.0 | 8.293 | 2.309 | 0.021 | 0.042 |
| B-C | 0.5 | 8.293 | 0.144 | 0.885 | 0.885 |
Cuadro de Agrupamiento
| Suma (RanK) | Grupos | |
|---|---|---|
| B | 15.0 | a |
| C | 14.5 | a |
| A | 6.5 | b |
El estadístico de la prueba es 8.2727 y el P-valor$=$ 0.016 < 5% entonces, en el nivel de significancia del 5% hay evidencia de que los factores no son todos iguales.
En el cuadro de Comparación Múltiple podemos ver que existen diferencias significativas entre los factores A y B y entre los factores A y C.
Al observar los rank en el cuadro de agrupación. vemos que las respuestas para los factores B y C son mayores que las respuestas al factor A.