1. Prueba de Kruskal-Wallis
La prueba de Kruskal-Wallis es una prueba de hipótesis no paramétrica utilizada para comparar tres o más poblaciones. Se utiliza para probar la hipótesis nula de que todas las poblaciones tienen la misma función de distribución contra la hipótesis alternativa de que al menos dos de ellas tienen diferentes funciones de distribución.
Ejemplo:
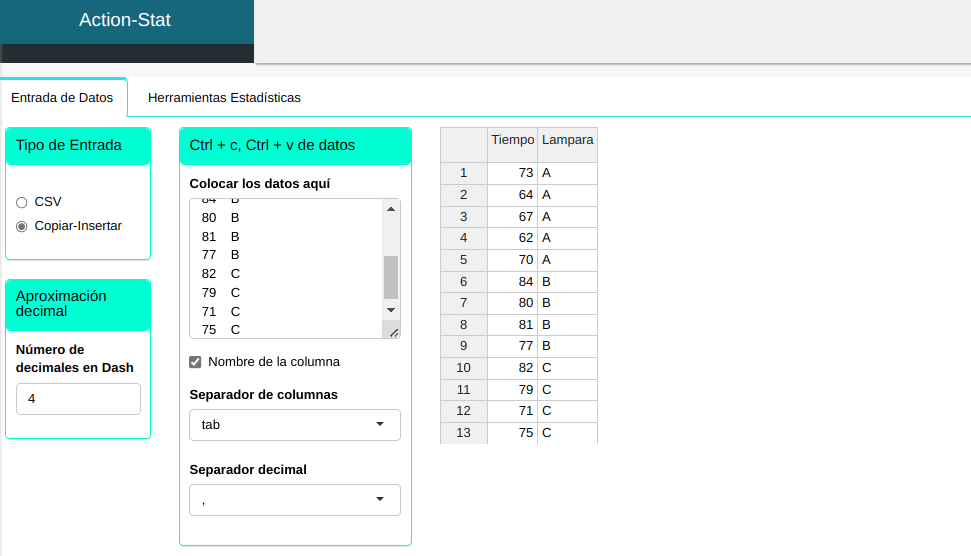
Se seleccionó una muestra aleatoria de tres tipos diferentes de lámparas y se probó para ver por cuánto tiempo funcionaban las lámparas.
| Tiempo | Lámpara |
|---|---|
| 73 | A |
| 64 | A |
| 67 | A |
| 62 | A |
| 70 | A |
| 84 | B |
| 80 | B |
| 81 | B |
| 77 | B |
| 82 | C |
| 79 | C |
| 71 | C |
| 75 | C |
Subiremos los resultados en sistema.
La prueba de Kruskal-Wallis se realizará utilizando la configuración que se muestra en la siguiente figura.
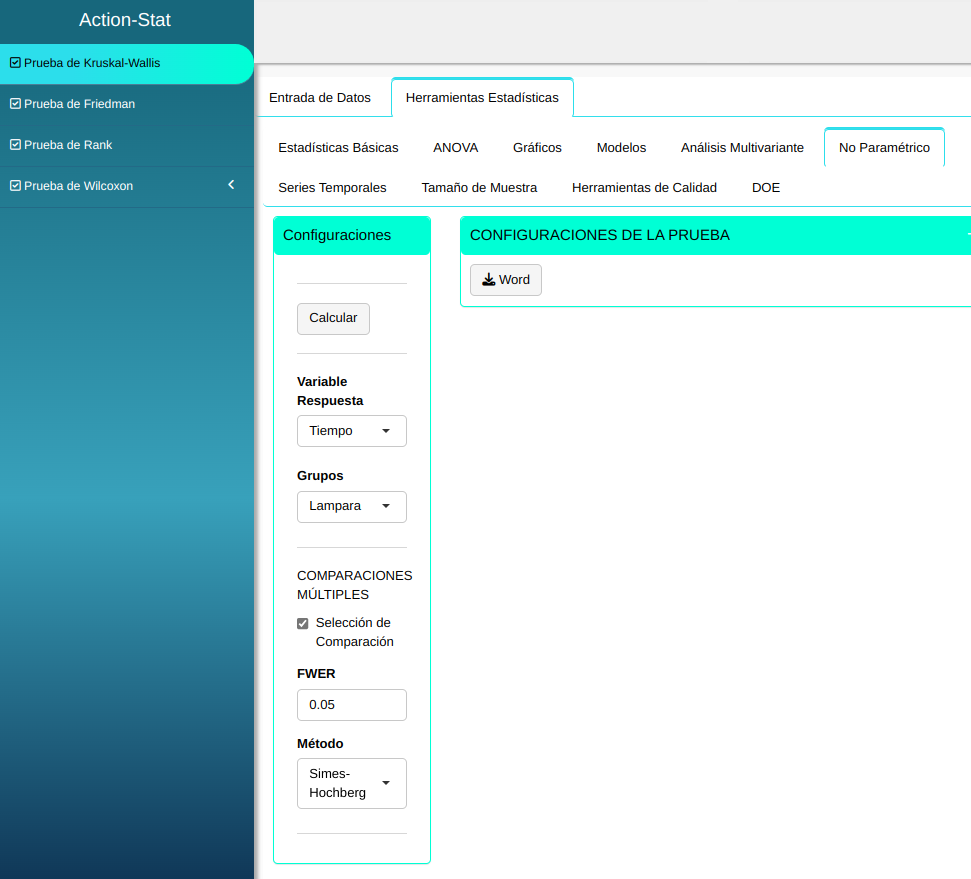
Pulsando en Calcular obtenemos los resultados. También se puede generar y descargar los resultados en un archivo Word.

Los resultados son:
Prueba de Kruskal-Wallis
| Valor | |
|---|---|
| Kruskal-Wallis Chi-cuadrado | 8.403 |
| Grados de Libertad | 2.000 |
| P-valor | 0.015 |
Cuadro de Comparación Múltiple - FWER (Comparación Múltiple)
| Diferencia observada | Estadísticas | Límite inferior | Límite superior | P-valor ajustado | |
|---|---|---|---|---|---|
| ''A-B'' | -7.30 | 4.659 | -10.791 | -3.809 | 0.0027 |
| ''A-C'' | -5.05 | 3.223 | -8.541 | -1.559 | 0.0183 |
| ''B-C'' | 2.25 | 1.362 | -1.430 | 5.930 | 0.203 |
Cuadro de Agrupamiento
| Medias (Rank) | Grupos | |
|---|---|---|
| B | 10.50 | a |
| C | 8.25 | a |
| A | 3.20 | b |
El estadístico de prueba es $ \chi^2 = 8.4$, Como P-valor=0.0149 rechazamos la hipótesis nula de que, en media, las tres lámparas tienen el mismo tiempo de funcionamiento. Por lo tanto, concluimos que al menos una de ellas tiene un tiempo medio de funcionamiento diferente al de los demás.
En el cuadro de Comparaciones múltiples, mientras que el tiempo de funcionamiento de las lámparas B y C son similares el P-valor del factor comparado B−C es igual a 0.20297, lámparas tipo A tienen un tiempo de funcionamiento más corto que los otros tipos de lámparas porque los factores comparados A−B y A−C tienen p-valores de 0.0027 y 0.01825 respectivamente.