3. Prueba de Rank
La prueba de Rank es el método más popular para comparar curvas de supervivencia. Esta prueba es importante cuando queremos comparar un nuevo proceso con uno antiguo, comparar dos productos diferentes en términos de vida útil o incluso determinar si dos curvas de supervivencia tiene diferencias significativas entre ellos.
Ejemplo 1:
Un productor de requesón realiza una prueba de caducidad de su producto. Su producto se vende a temperatura ambiente y sin conservantes. El evento de interés es la aparición de algún hongo en el producto. Los datos se muestran a continuación, con el tiempo medido en horas. El símbolo + indica censura.
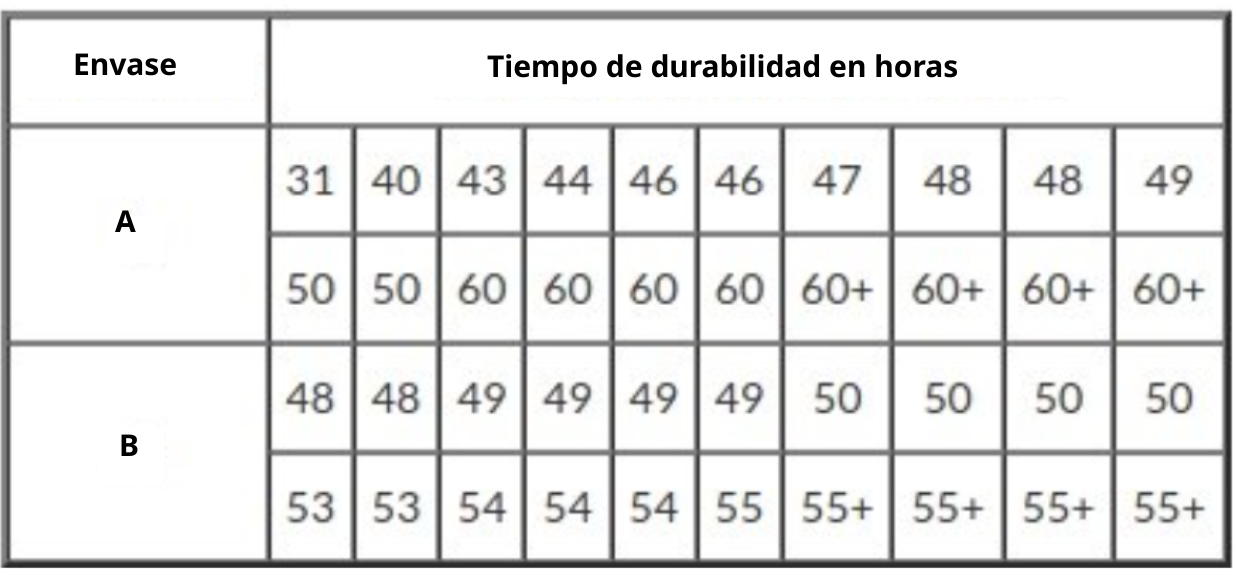
¿Hay una diferencia entre los dos envases en términos de durabilidad del producto? Vamos Comparar los tiempos de durabilidad usando la prueba de Rank. Primero, organizaremos los datos en un nuevo cuadro, en la que reemplazamos el símbolo + con el indicador 0 (censura) y para los demás valores ponemos el indicador 1 (fallo).
| Tiempo | Censura | Grupo |
|---|---|---|
| 31 | 1 | A |
| 40 | 1 | A |
| 43 | 1 | A |
| 44 | 1 | A |
| 46 | 1 | A |
| 46 | 1 | A |
| 47 | 1 | A |
| 48 | 1 | A |
| 48 | 1 | A |
| 49 | 1 | A |
| 50 | 1 | A |
| 50 | 1 | A |
| 60 | 1 | A |
| 60 | 1 | A |
| 60 | 1 | A |
| 60 | 1 | A |
| 60 | 0 | A |
| 60 | 0 | A |
| 60 | 0 | A |
| 60 | 0 | A |
| 48 | 1 | B |
| 48 | 1 | B |
| 49 | 1 | B |
| 49 | 1 | B |
| 49 | 1 | B |
| 49 | 1 | B |
| 50 | 1 | B |
| 50 | 1 | B |
| 50 | 1 | B |
| 50 | 1 | B |
| 53 | 1 | B |
| 53 | 1 | B |
| 54 | 1 | B |
| 54 | 1 | B |
| 54 | 1 | B |
| 55 | 1 | B |
| 55 | 0 | B |
| 55 | 0 | B |
| 55 | 0 | B |
| 55 | 0 | B |
Cargaremos los datos en el sistema.
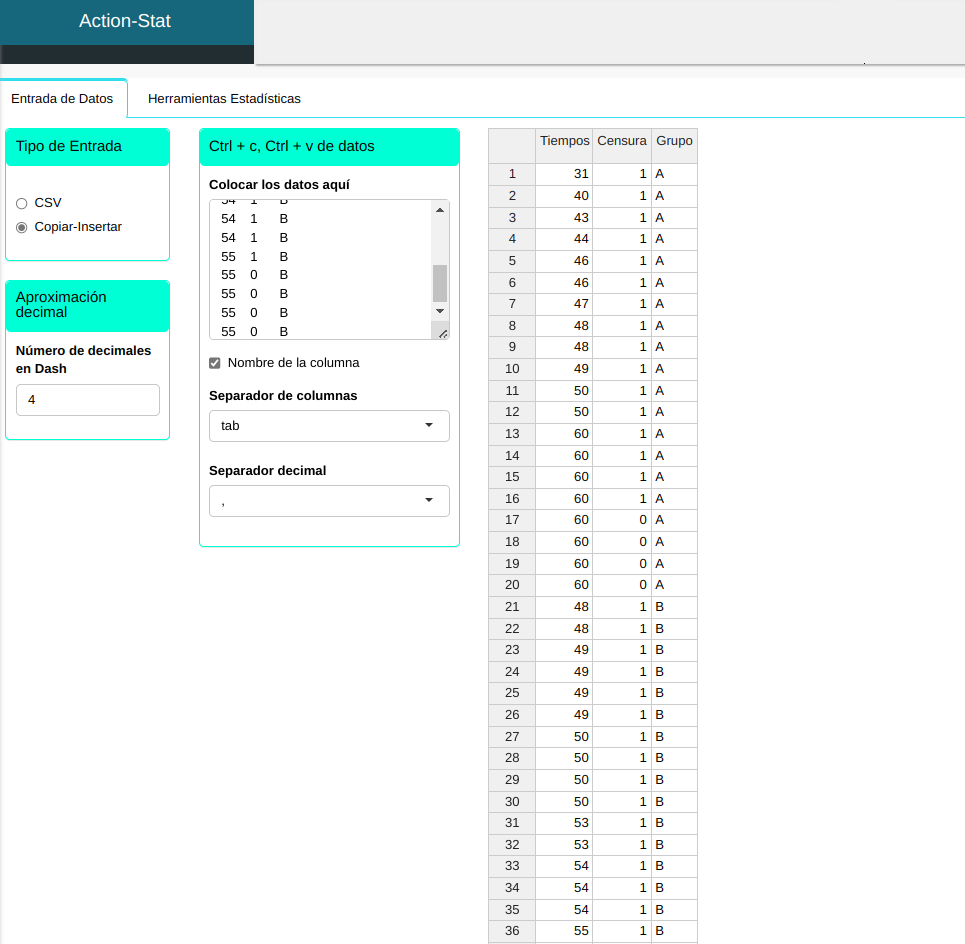
La prueba de Rank se llevará a cabo utilizando las configuraciones que se muestran en la siguiente figura.
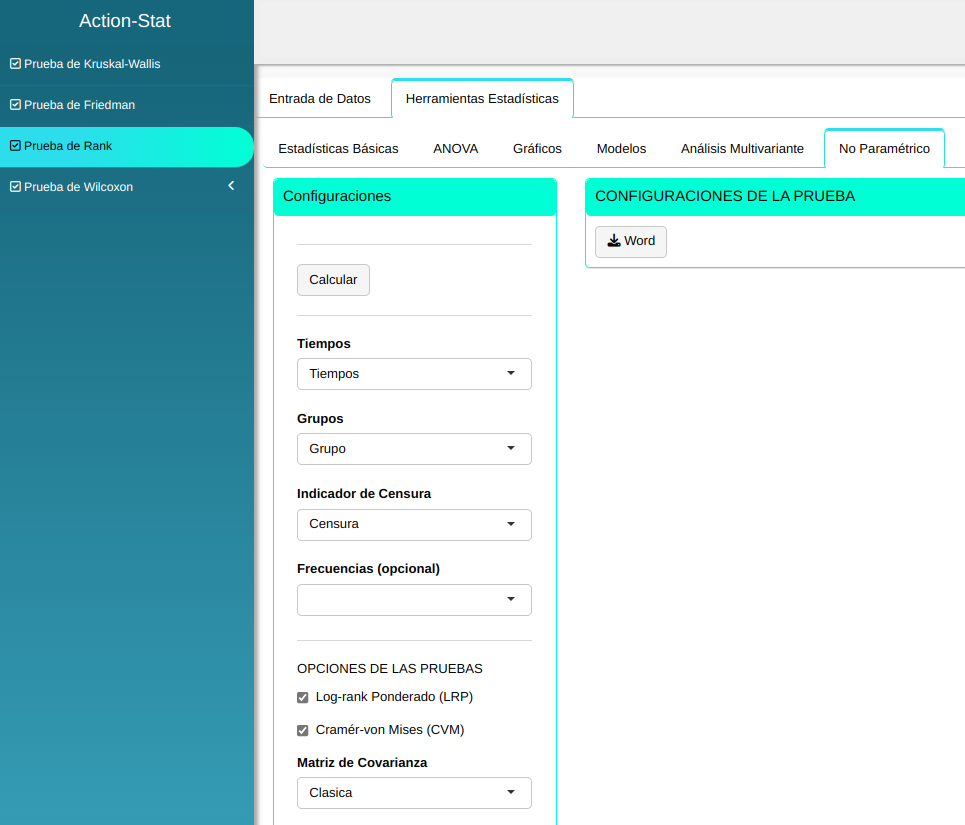
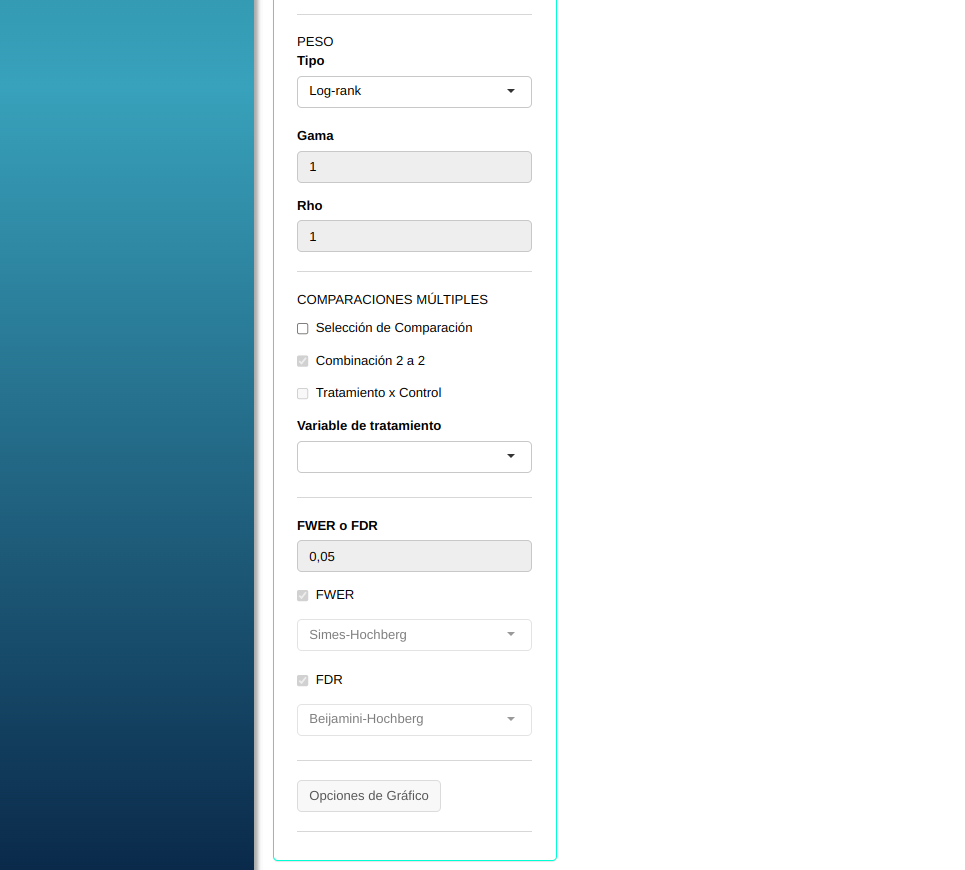
Al hacer clic en calcular obtenemos los resultados y también se puede descargar los resultados en un archivo Word.
Los resultados son:
Comparación de grupos
| Peso | Estadísticas | P-valor | |
|---|---|---|---|
| Cramér-von Mises (CVM) 1 | LogRank | 47.4734 | 0.1104 |
| Rango logarítmico ponderado (LRP) 1 | LogRank | 0.0064 | 0.9364 |
Resumen de la comparación de grupos
| Grupos | Tiempo | Número de eventos | Cantidad en riesgo | Desviación Estándar | Función Supervivencia | Límite inferior | Límite superior | Función de Intensidad | Límite inferior.1 | Límite superior.1 |
|---|---|---|---|---|---|---|---|---|---|---|
| A | 31.0000 | 1.0000 | 20.0000 | 0.0487 | 0.9500 | 0.8540 | 1.0000 | 0.0500 | 0.0452 | 0.0548 |
| A | 40.0000 | 1.0000 | 19.0000 | 0.0671 | 0.9000 | 0.7690 | 1.0000 | 0.1000 | 0.0869 | 0.1131 |
| A | 43.0000 | 1.0000 | 18.0000 | 0.0798 | 0.8500 | 0.6940 | 1.0000 | 0.1500 | 0.1265 | 0.1735 |
| A | 44.0000 | 1.0000 | 17.0000 | 0.0894 | 0.8000 | 0.6250 | 0.9750 | 0.2000 | 0.1649 | 0.2351 |
| A | 46.0000 | 2.0000 | 16.0000 | 0.1020 | 0.7000 | 0.4990 | 0.9010 | 0.3000 | 0.2397 | 0.3603 |
| A | 47.0000 | 1.0000 | 14.0000 | 0.1070 | 0.6500 | 0.4410 | 0.8590 | 0.3500 | 0.2768 | 0.4232 |
| A | 48.0000 | 2.0000 | 13.0000 | 0.1110 | 0.5500 | 0.3320 | 0.7680 | 0.4500 | 0.3519 | 0.5481 |
| A | 49.0000 | 1.0000 | 11.0000 | 0.1120 | 0.5000 | 0.2810 | 0.7190 | 0.5000 | 0.3904 | 0.6096 |
| A | 50.0000 | 2.0000 | 10.0000 | 0.1100 | 0.4000 | 0.1850 | 0.6150 | 0.6000 | 0.4712 | 0.7288 |
| A | 60.0000 | 4.0000 | 8.0000 | 0.0894 | 0.2000 | 0.0247 | 0.3750 | 0.8000 | 0.6598 | 0.9402 |
| B | 48.0000 | 2.0000 | 20.0000 | 0.0671 | 0.9000 | 0.7690 | 1.0000 | 0.1000 | 0.0869 | 0.1131 |
| B | 49.0000 | 4.0000 | 18.0000 | 0.1020 | 0.7000 | 0.4990 | 0.9010 | 0.3000 | 0.2397 | 0.3603 |
| B | 50.0000 | 4.0000 | 14.0000 | 0.1120 | 0.5000 | 0.2810 | 0.7190 | 0.5000 | 0.3904 | 0.6096 |
| B | 53.0000 | 2.0000 | 10.0000 | 0.1100 | 0.4000 | 0.1850 | 0.6150 | 0.6000 | 0.4712 | 0.7288 |
| B | 54.0000 | 3.0000 | 8.0000 | 0.0968 | 0.2500 | 0.0602 | 0.4400 | 0.7500 | 0.6077 | 0.8923 |
| B | 55.0000 | 1.0000 | 5.0000 | 0.0894 | 0.2000 | 0.0247 | 0.3750 | 0.8000 | 0.6598 | 0.9402 |
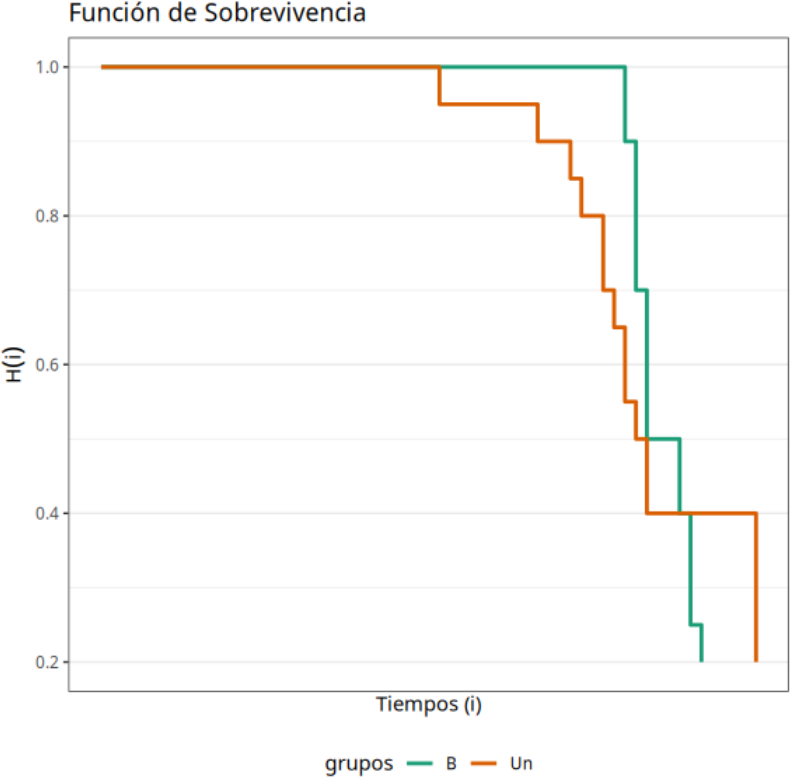
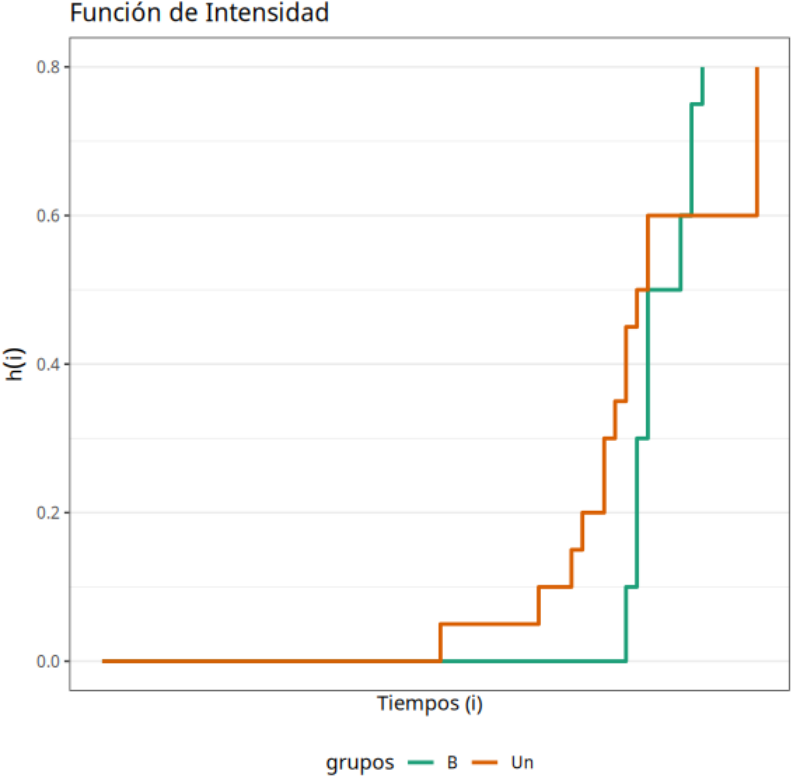
Sabiendo que la “Prueba de Rank” se utiliza para probar la hipótesis nula de que no hay diferencia entre los grupos (A y B) concluimos que, según el P-valor = 0.9362, no deberíamos rechazar la hipótesis nula. Por lo tanto, decimos que no hay diferencia significativa entre los dos envases con relación a la durabilidad del producto.
Ejemplo 2:
Un productor de requesón realiza una prueba de caducidad de su producto. Su producto se vende a temperatura ambiente y sin conservantes. El evento de interés es la aparición de algún hongo en el producto. Los datos se muestran a continuación, con el tiempo medido en horas. El símbolo + indica censura.

¿Hay una diferencia entre los dos envase en términos de durabilidad del producto? Vamos Comparar los tiempos de durabilidad usando la prueba de Rank.
Primero, organizaremos los datos en un nuevo cuadro, en la que reemplazamos el símbolo + con el indicador 0 (censura) y para los demás valores ponemos el indicador 1 (fallo).
Para trabajar con datos resumidos, debemos crear la siguiente tabla:
| Tiempo | Censura | Grupo | Frecuencia |
|---|---|---|---|
| 31 | 1 | A | 1 |
| 40 | 1 | A | 1 |
| 43 | 1 | A | 1 |
| 44 | 1 | A | 1 |
| 46 | 1 | A | 2 |
| 47 | 1 | A | 1 |
| 48 | 1 | A | 2 |
| 48 | 1 | B | 2 |
| 49 | 1 | A | 1 |
| 49 | 1 | B | 4 |
| 50 | 1 | A | 2 |
| 50 | 1 | B | 4 |
| 53 | 1 | B | 2 |
| 54 | 1 | B | 3 |
| 55 | 1 | B | 1 |
| 55 | 0 | B | 4 |
| 60 | 1 | A | 4 |
| 60 | 0 | A | 4 |
Cargaremos los datos en el sistema.
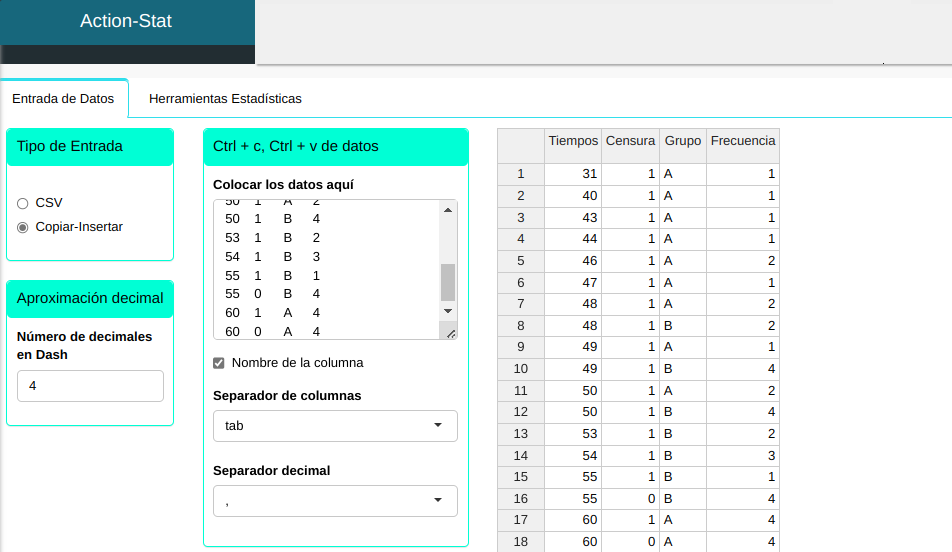
La prueba de Rank se llevará a cabo utilizando las configuraciones que se muestran en la siguiente figura.
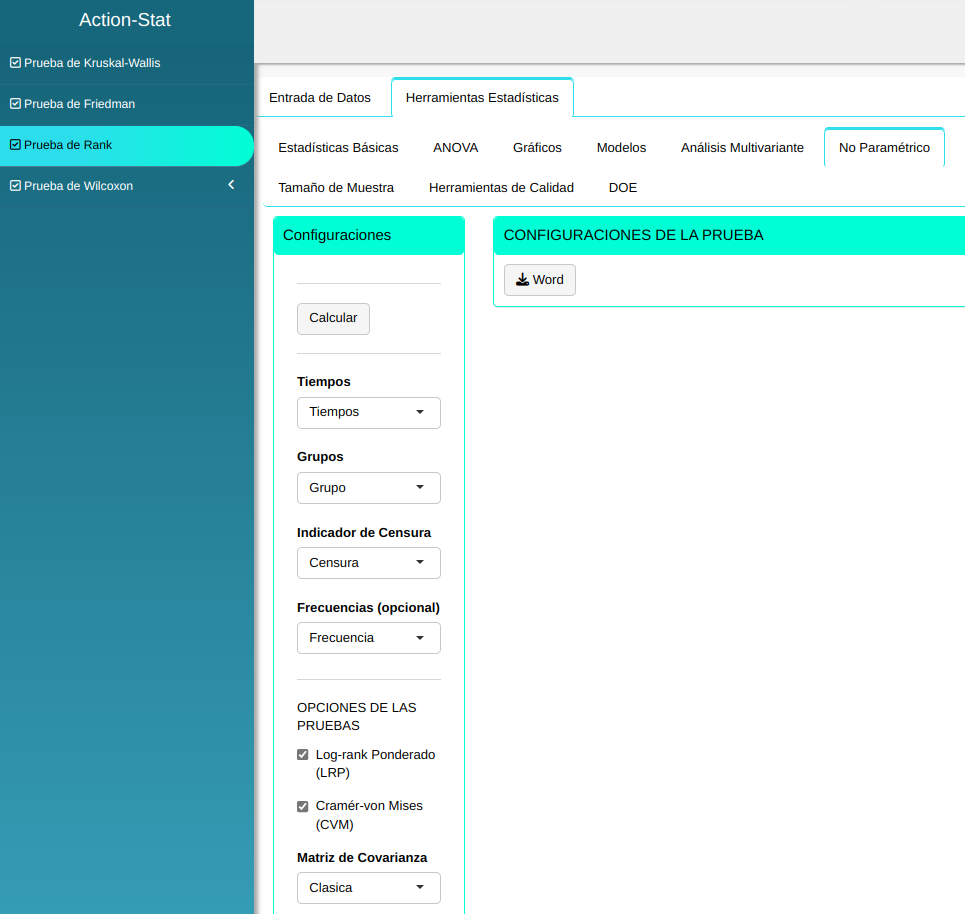
Al clicar en calcular obtendremos los resultados. También puedes descargar los resultados en un archivo de Word.
Los resultados son:
Comparación de grupos
| Peso | Estadísticas | P-valor | |
|---|---|---|---|
| Cramér-von Mises (CVM) 1 | Log Rank | 47.473 | 0.110 |
| Log Rank ponderado (LRP) 1 | Log Rank | 0.006 | 0.936 |
Resumen de comparación de los grupos
| Grupos | Tiempo | Número de eventos | Cantidad en riesgo | Desviación Estándar | Función de supervivencia | Límite inferior | Límite superior | Función de intensidad | Límite inferior.1 | Límite superior.1 |
|---|---|---|---|---|---|---|---|---|---|---|
| A | 31 | 1 | 20 | 0.049 | 0.95 | 0.854 | 1 | 0.05 | 0.045 | 0.055 |
| A | 40 | 1 | 19 | 0.067 | 0.9 | 0.769 | 1 | 0.1 | 0.087 | 0.113 |
| A | 43 | 1 | 18 | 0.08 | 0.85 | 0.694 | 1 | 0.15 | 0.127 | 0.173 |
| A | 44 | 1 | 17 | 0.089 | 0.8 | 0.625 | 0.975 | 0.2 | 0.165 | 0.235 |
| A | 46 | 2 | 16 | 0.102 | 0.7 | 0.499 | 0.901 | 0.3 | 0.24 | 0.36 |
| A | 47 | 1 | 14 | 0.107 | 0.65 | 0.441 | 0.859 | 0.35 | 0.277 | 0.423 |
| A | 48 | 2 | 13 | 0.111 | 0.55 | 0.332 | 0.768 | 0.45 | 0.352 | 0.548 |
| A | 49 | 1 | 11 | 0.112 | 0.5 | 0.281 | 0.719 | 0.5 | 0.39 | 0.61 |
| A | 50 | 2 | 10 | 0.11 | 0.4 | 0.185 | 0.615 | 0.6 | 0.471 | 0.729 |
| A | 60 | 4 | 8 | 0.089 | 0.2 | 0.025 | 0.375 | 0.8 | 0.66 | 0.94 |
| B | 48 | 2 | 20 | 0.067 | 0.9 | 0.769 | 1 | 0.1 | 0.087 | 0.113 |
| B | 49 | 4 | 18 | 0.102 | 0.7 | 0.499 | 0.901 | 0.3 | 0.24 | 0.36 |
| B | 50 | 4 | 14 | 0.112 | 0.5 | 0.281 | 0.719 | 0.5 | 0.39 | 0.61 |
| B | 53 | 2 | 10 | 0.11 | 0.4 | 0.185 | 0.615 | 0.6 | 0.471 | 0.729 |
| B | 54 | 3 | 8 | 0.097 | 0.25 | 0.06 | 0.44 | 0.75 | 0.608 | 0.892 |
| B | 55 | 1 | 5 | 0.089 | 0.2 | 0.025 | 0.375 | 0.8 | 0.66 | 0.94 |
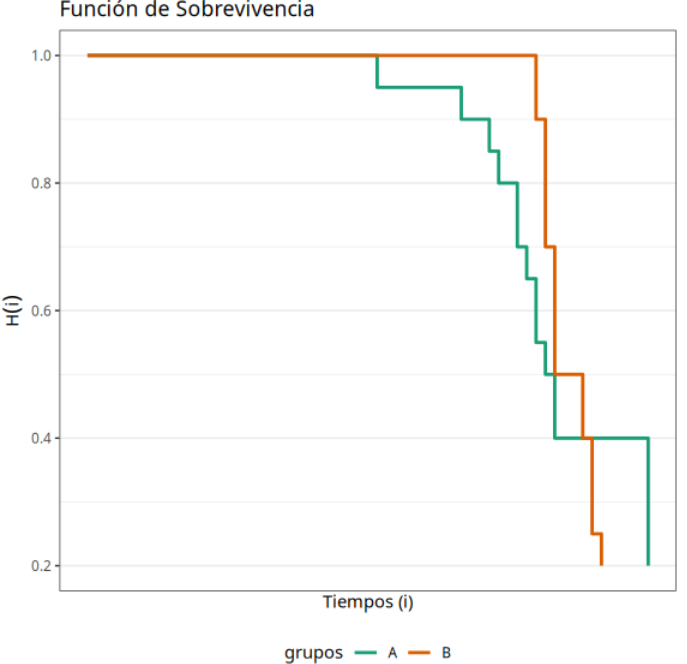
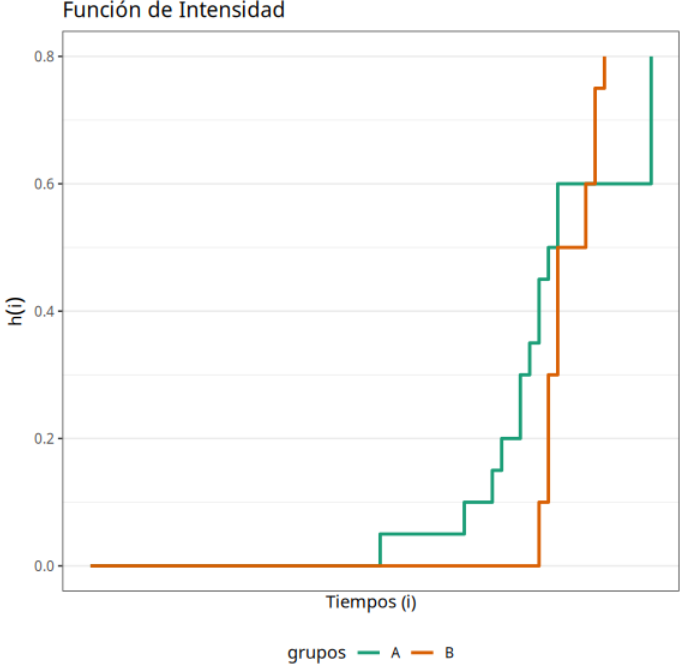
Sabiendo que la prueba de Rank se utiliza para probar la hipótesis nula de que no hay diferencia entre los grupos (A y B) concluimos que, según P-valor= 0.5399. no debemos rechazar la hipótesis nula. Por lo tanto. decimos que no hay diferencia significativa entre los dos envases en cuanto a la durabilidad del producto.