4. Prueba de Wilcoxon
Utilizando la prueba de Wilcoxon, comprobamos la pseudo medianas, para muestras únicas, muestras independientes y muestras pareadas.
Ejemplo 1:
Suponiendo que los números de la muestra están distribuidos simétricamente alrededor de la mediana, usaremos la prueba de Wilcoxon para probar la hipótesis $H_0: \theta_0$= 220 donde la mediana es igual a 220. en el nivel de significancia del 5%.
| Datos |
|---|
| 126 |
| 142 |
| 156 |
| 228 |
| 245 |
| 246 |
| 370 |
| 419 |
| 433 |
| 454 |
| 478 |
| 503 |
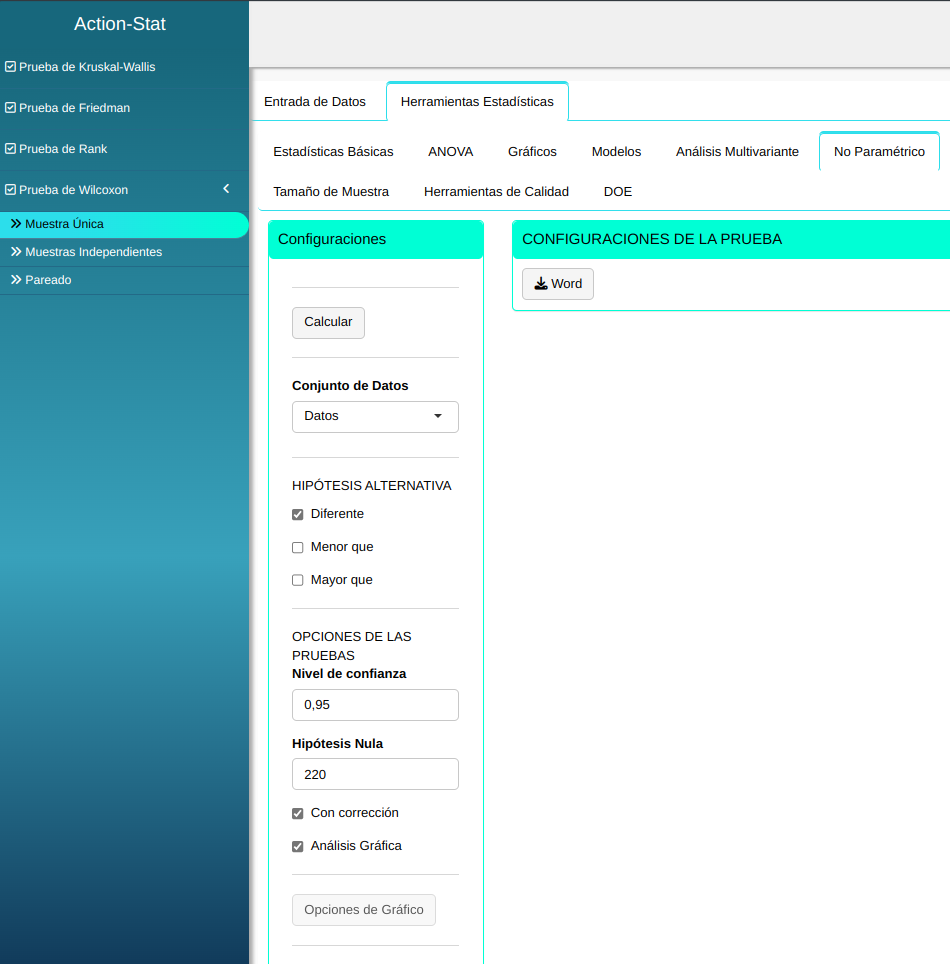
La prueba de Wilcoxon se llevará a cabo utilizando los ajustes que se muestran en la siguiente figura.
Al hacer un clic en calcular obtenemos los resultados. También se puede descargar los resultados en un archivo Word.

Los resultados son:
Cuadro de estadísticas de prueba (Wilcoxon)
| Valores | |
|---|---|
| Estadísticas | 63 |
| P-valor | 0.064 |
| Hipótesis nula | 220 |
| Límite inferior | 200.5 |
| (Pseudo) mediana | 315.75 |
| Límite superior | 433 |
| Nivel de confianza | 0.95 |
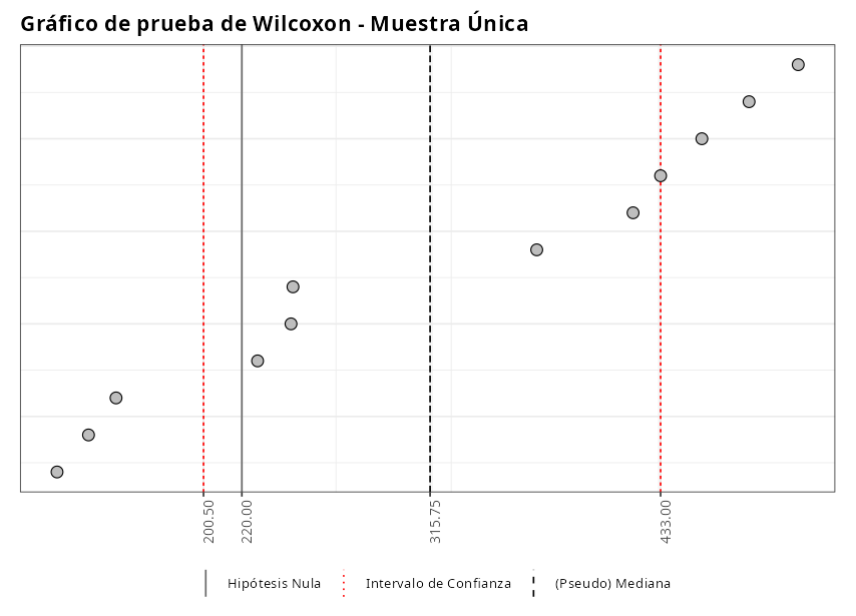
El estadístico de prueba es V = 63. Como el P-valor es igual a 0.0639 = 6.39% > 5% no rechazamos la hipótesis nula de que $\theta_0$ = 220 en el nivel de 5% de significancia.
Ejemplo 2:
Dos muestras proporcionaron los siguientes valores para una determinada variable.
| Muestras | Datos |
|---|---|
| Muestra 1 | 29 |
| Muestra 1 | 39 |
| Muestra 1 | 60 |
| Muestra 1 | 78 |
| Muestra 1 | 82 |
| Muestra 1 | 112 |
| Muestra 1 | 125 |
| Muestra 1 | 170 |
| Muestra 1 | 192 |
| Muestra 1 | 224 |
| Muestra 1 | 263 |
| Muestra 1 | 275 |
| Muestra 1 | 276 |
| Muestra 1 | 286 |
| Muestra 1 | 369 |
| Muestra 1 | 756 |
| Muestra 2 | 126 |
| Muestra 2 | 142 |
| Muestra 2 | 156 |
| Muestra 2 | 228 |
| Muestra 2 | 245 |
| Muestra 2 | 246 |
| Muestra 2 | 370 |
| Muestra 2 | 419 |
| Muestra 2 | 433 |
| Muestra 2 | 454 |
| Muestra 2 | 478 |
| Muestra 2 | 503 |
Subiremos los datos al sistema.
La prueba de Wilcoxon se llevará a cabo utilizando los ajustes que se muestran en la siguiente figura.
Al hacer un clic en calcular obtenemos los resultados. También se puede descargar los resultados en un archivo Word.

Los resultados son:
Cuadro de estadísticas de prueba (Wilcoxon)
| Valores | |
|---|---|
| Estadísticas | 141 |
| P-valor | 0.0373 |
| Hipótesis nula | 0 |
| Límite inferior | 4 |
| (Pseudo) mediana | 133.5 |
| Límite superior | 240 |
| Nivel de confianza | 0.95 |
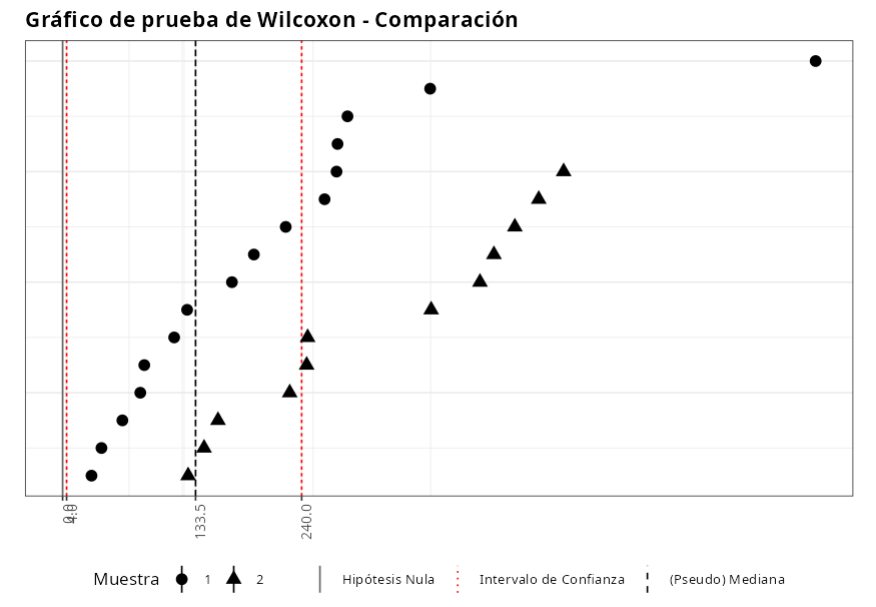
El estadístico de prueba es W = 141. Dado que el P-valor es igual a 0.0373 = 3.73% < 5%, rechazamos la hipótesis nula. Así, tenemos evidencia de que las muestras provienen de poblaciones que tienen medianas diferentes.
Ejemplo 3:
Consideremos dos muestras dependientes cuyos datos están en el siguiente cuadro. ¿Existe evidencia de una diferencia entre las dos muestras?
| Muestra 1 | Muestra 2 |
|---|---|
| 564 | 557 |
| 521 | 505 |
| 495 | 465 |
| 564 | 562 |
| 560 | 545 |
| 481 | 448 |
| 545 | 531 |
| 478 | 458 |
| 580 | 562 |
| 484 | 485 |
| 539 | 520 |
| 467 | 445 |
Subiremos los datos al sistema.
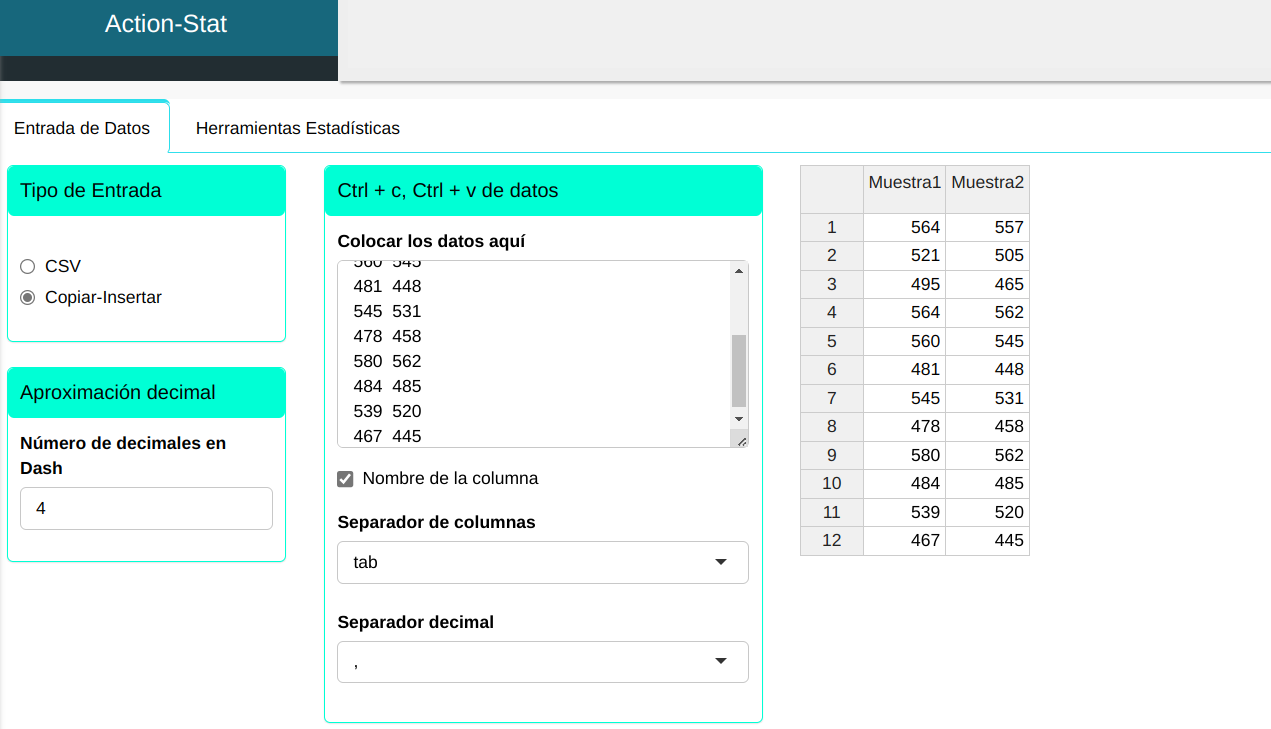
La prueba de Wilcoxon se llevará a cabo utilizando los ajustes que se muestran en la siguiente figura.
Al hacer un clic en calcular obtenemos los siguientes resultados. También se puede descargar los resultados en un archivo Word.

Los resultados son:
Cuadro estadísticas de prueba (Wilcoxon)
| Valores | |
|---|---|
| Estadísticas | 77 |
| P-valor | 0.001 |
| Hipótesis nula | 0 |
| Límite inferior | 9 |
| (Pseudo) mediana | 16.75 |
| Límite superior | 23.5 |
| Nivel de confianza | 0.95 |
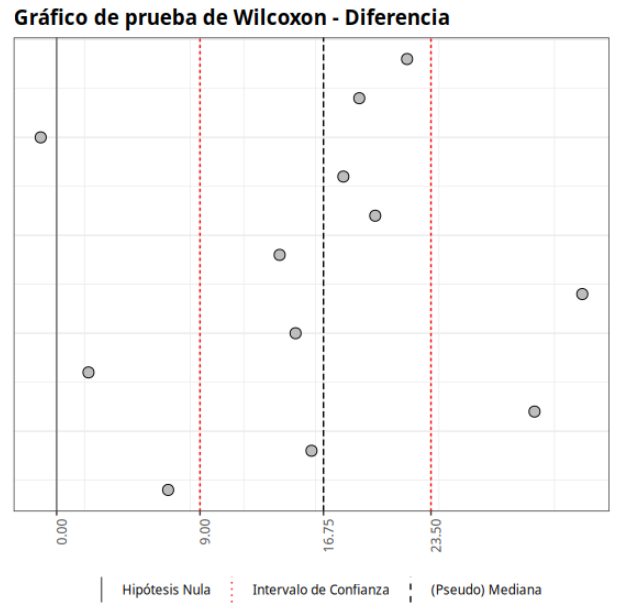
El estadístico de prueba es W = 77. Como el P-valor = 0.000976563 < 0.05 entonces, al nivel de significancia del 5% hay evidencia de una diferencia significativa entre las dos muestras.