1. Suavización Exponencial
El modelo de suavización exponencial es un método de previsiones que se basa en la idea de que las observaciones pasadas contienen información relevante sobre el modelo estándar de la serie temporal.
Ejemplo:
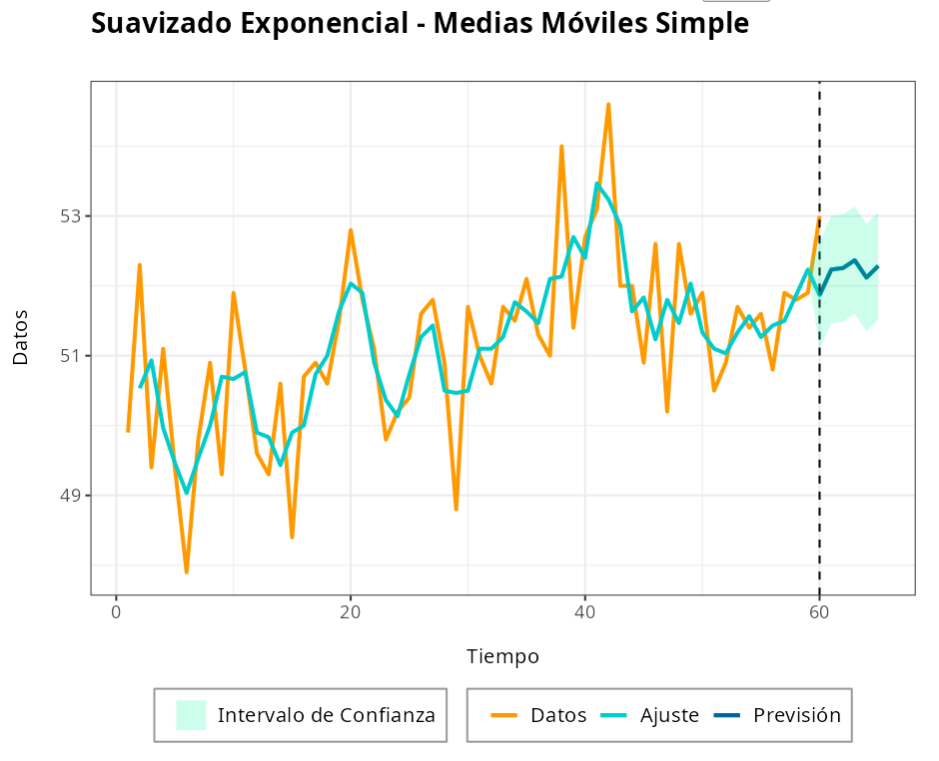
Consideremos los datos sobre las temperaturas medias anuales en la ciudad de Nueva York para los años 1912 y 1971. Vamos a ajustar un modelo simple de media móvil a esta serie temporal y predecir la temperatura en los próximos 5 años.
| Año | Temperatura |
|---|---|
| 1912 | 49.9 |
| 1913 | 52.3 |
| 1914 | 49.4 |
| 1915 | 51.1 |
| 1916 | 49.4 |
| 1917 | 47.9 |
| 1918 | 49.8 |
| 1919 | 50.9 |
| 1920 | 49.3 |
| 1921 | 51.9 |
| 1922 | 50.8 |
| 1923 | 49.6 |
| 1924 | 49.3 |
| 1925 | 50.6 |
| 1926 | 48.4 |
| 1927 | 50.7 |
| 1928 | 50.9 |
| 1929 | 50.6 |
| 1930 | 51.5 |
| 1931 | 52.8 |
| 1932 | 51.8 |
| 1933 | 51.1 |
| 1934 | 49.8 |
| 1935 | 50.2 |
| 1936 | 50.4 |
| 1937 | 51.6 |
| 1938 | 51.8 |
| 1939 | 50.9 |
| 1940 | 48.8 |
| 1941 | 51.7 |
| 1942 | 51.0 |
| 1943 | 50.6 |
| 1944 | 51.7 |
| 1945 | 51.5 |
| 1946 | 52.1 |
| 1947 | 51.3 |
| 1948 | 51.0 |
| 1949 | 54.0 |
| 1950 | 51.4 |
| 1951 | 52.7 |
| 1952 | 53.1 |
| 1953 | 54.6 |
| 1954 | 52.0 |
| 1955 | 52.0 |
| 1956 | 50.9 |
| 1957 | 52.6 |
| 1958 | 50.2 |
| 1959 | 52.6 |
| 1960 | 51.6 |
| 1961 | 51.9 |
| 1962 | 50.5 |
| 1963 | 50.9 |
| 1964 | 51.7 |
| 1965 | 51.4 |
| 1966 | 51.7 |
| 1967 | 50.8 |
| 1968 | 51.9 |
| 1969 | 51.8 |
| 1970 | 51.9 |
| 1971 | 53.0 |
Subiremos los datos al sistema.
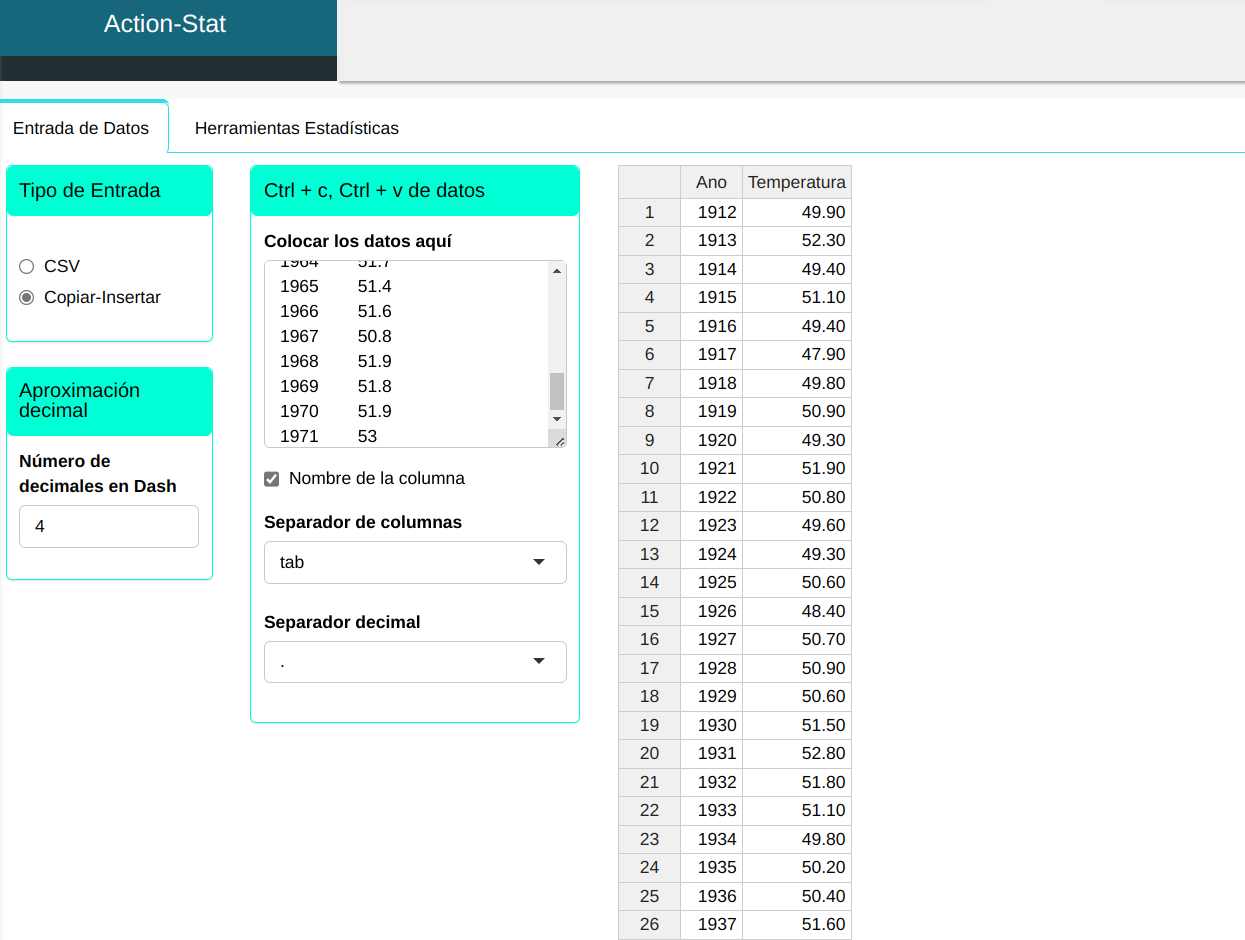
Realizaremos el análisis ajustando conforme la figura de abajo.
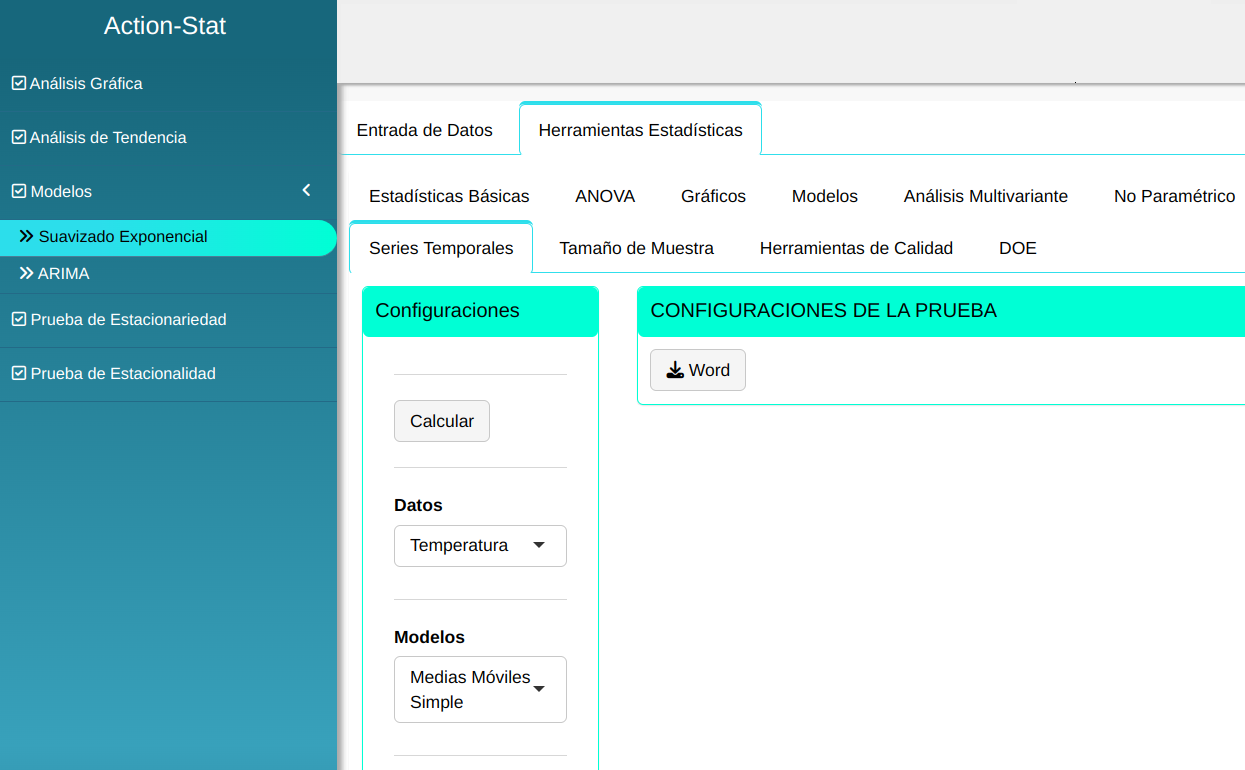
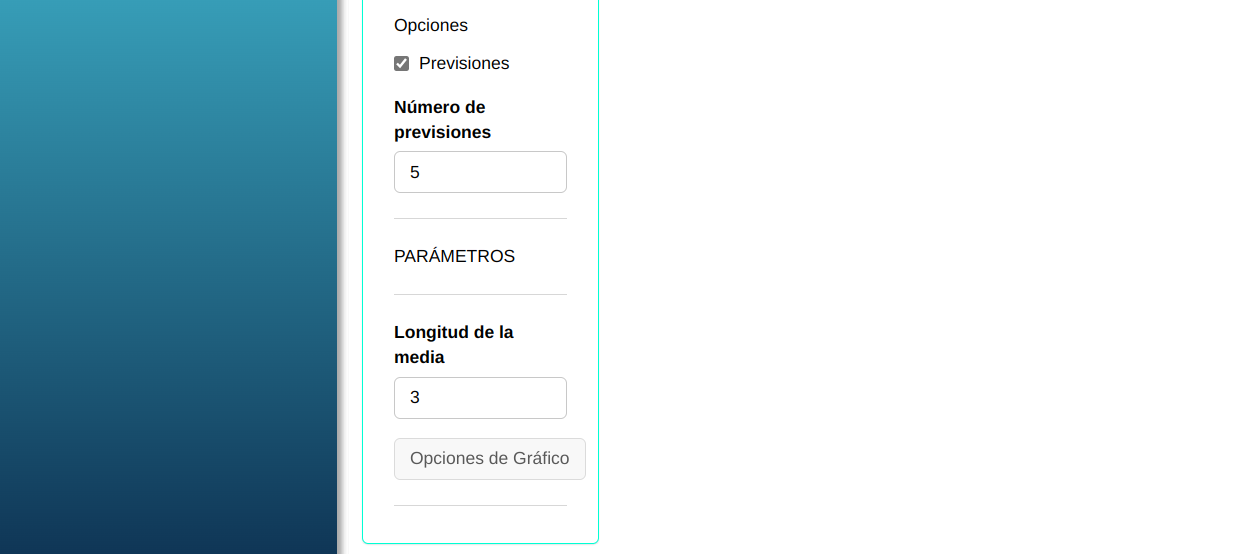
En seguida, haga un clic en Calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.
Los resultados son:
Medidas de Exactitud
| V1 | |
|---|---|
| MAPE | 1.3430128 |
| MAD | 0.6853801 |
| MSD | 0.6561014 |
Longitud de la Media
| k |
| 3 |
Cuadro de estimaciones
| Datos | Ajuste | Residuos |
|---|---|---|
| 49.9 | ||
| 52.3 | ||
| 49.4 | 50.53333 | -1.13333333 |
| 51.1 | 50.93333 | 0.16666667 |
| 49.4 | 49.96667 | -0.56666667 |
| 47.9 | 49.46667 | -1.56666667 |
| 49.8 | 49.03333 | 0.76666667 |
| 50.9 | 49.53333 | 1.36666667 |
| 49.3 | 50 | -0.7 |
| 51.9 | 50.7 | 1.2 |
| 50.8 | 50.66667 | 0.13333333 |
| 49.6 | 50.76667 | -1.16666667 |
| 49.3 | 49.9 | -0.6 |
| 50.6 | 49.83333 | 0.76666667 |
| 48.4 | 49.43333 | -1.03333333 |
| 50.7 | 49.9 | 0.8 |
| 50.9 | 50 | 0.9 |
| 50.6 | 50.73333 | -0.13333333 |
| 51.5 | 51 | 0.5 |
| 52.8 | 51.63333 | 1.16666667 |
| 51.8 | 52.03333 | -0.23333333 |
| 51.1 | 51.9 | -0.8 |
| 49.8 | 50.9 | -1.1 |
| 50.2 | 50.36667 | -0.16666667 |
| 50.4 | 50.13333 | 0.26666667 |
| 51.6 | 50.73333 | 0.86666667 |
| 51.8 | 51.26667 | 0.53333333 |
| 50.9 | 51.43333 | -0.53333333 |
| 48.8 | 50.5 | -1.7 |
| 51.7 | 50.46667 | 1.23333333 |
| 51 | 50.5 | 0.5 |
| 50.6 | 51.1 | -0.5 |
| 51.7 | 51.1 | 0.6 |
| 51.5 | 51.26667 | 0.23333333 |
| 52.1 | 51.76667 | 0.33333333 |
| 51.3 | 51.63333 | -0.33333333 |
| 51 | 51.46667 | -0.46666667 |
| 54 | 52.1 | 1.9 |
| 51.4 | 52.13333 | -0.73333333 |
| 52.7 | 52.7 | 0 |
| 53.1 | 52.4 | 0.7 |
| 54.6 | 53.46667 | 1.13333333 |
| 52 | 53.23333 | -1.23333333 |
| 52 | 52.86667 | -0.86666667 |
| 50.9 | 51.63333 | -0.73333333 |
| 52.6 | 51.83333 | 0.76666667 |
| 50.2 | 51.23333 | -1.03333333 |
| 52.6 | 51.8 | 0.8 |
| 51.6 | 51.46667 | 0.13333333 |
| 51.9 | 52.03333 | -0.13333333 |
| 50.5 | 51.33333 | -0.83333333 |
| 50.9 | 51.1 | -0.2 |
| 51.7 | 51.03333 | 0.66666667 |
| 51.4 | 51.33333 | 0.06666667 |
| 51.7 | 51.6 | 0.1 |
| 50.8 | 51.3 | -0.5 |
| 51.9 | 51.46667 | 0.43333333 |
| 51.8 | 51.5 | 0.3 |
| 51.9 | 51.86667 | 0.03333333 |
| 53 | 52.23333 | 0.76666667 |
Previsiones
| Límite inferior de la Previsión | Previsión | Límite Superior de la Previsión |
|---|---|---|
| 51.09756 | 51.86667 | 52.63578 |
| 51.46422 | 52.23333 | 53.00244 |
| 51.48645 | 52.25556 | 53.02466 |
| 51.59756 | 52.36667 | 53.13578 |
| 51.34941 | 52.11852 | 52.88763 |
| 51.51608 | 52.28519 | 53.05429 |