4. Pruebas de Estacionariedad

Casi todos los modelos propuestos para las series temporales tienen como suposición la estacionariedad. Por lo tanto, una cuestión fundamental es saber cuándo una serie temporal es estacionaria. En la herramienta Pruebas de estacionariedad, hay tres pruebas disponibles para verificar la Estacionariedad de la serie.

Ejemplo:

Realizaremos la prueba para los siguientes datos:

AMBV3
84.06
83.85
83.56
83.47
83.27
82.81
82.20
82.06
81.62
80.77
81.30
81.92
82.75
82.77
82.84
82.82
82.72
82.29
81.18
80.11
80.27
80.21
79.92
79.96
80.19
80.17
80.17
79.85
81.00
80.44
79.96
79.85
79.82
80.11
80.20
80.31
81.18
80.81
81.15
81.32
81.21
81.40
81.10
81.40
82.27
82.15
81.78
81.69
81.34
81.88

---

Subiremos los datos al sistema.

Realizaremos el análisis ajustando conforme la figura abajo.

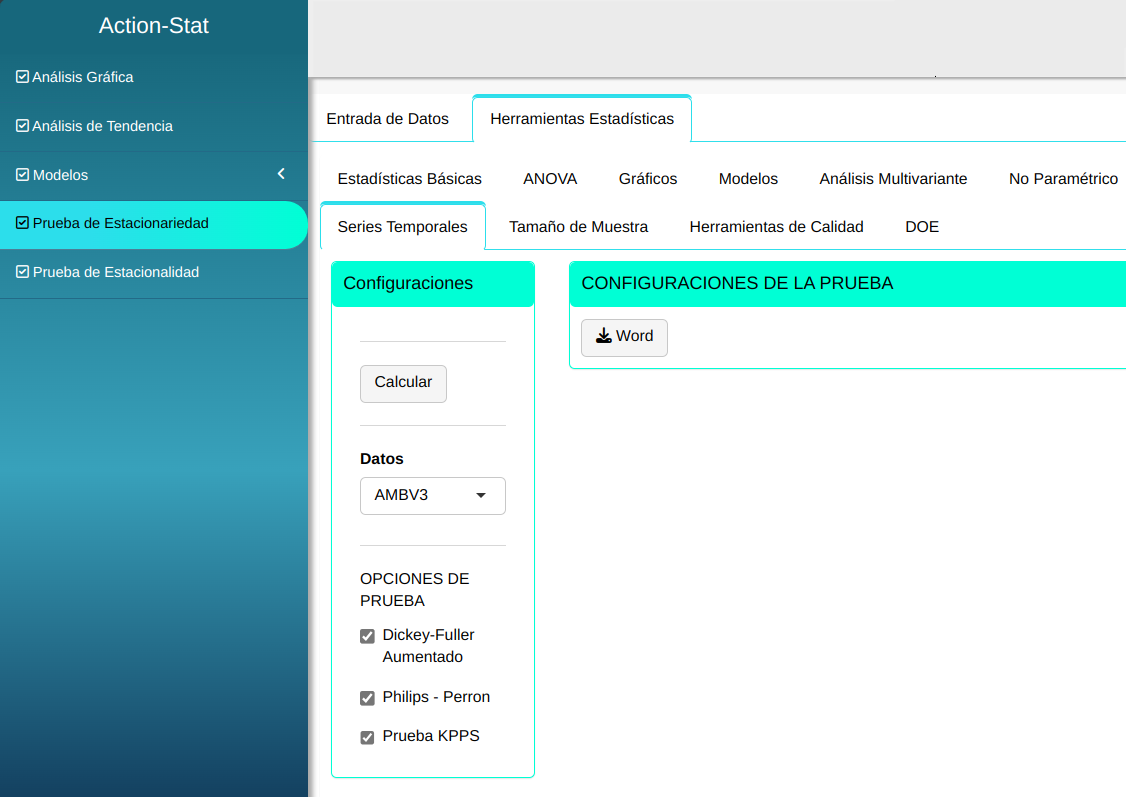
En seguida, haga un clic en Calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.

Los resultados son:

Test of Dickey-Fuller Aumentado

	Dickey-Fuller
Estadística	-1.90501089436462
P-valor	0.612390335192691
Tamaño de la Muestra	50
Hipótesis Nula	Existe por lo menos una raíz unitaria
Hipótesis Alternativa	No existe raíz unitaria

---

Test de Phillips-Perron

	Dickey-Fuller Z(alpha)
Estadística	-6.09026378709285
P-valor	0.753893665311693
Tamaño de la Muestra	50
Hipótesis Nula	Existe por lo menos una raíz unitaria
Hipótesis Alternativa	No existe raíz unitaria

---

Prueba KPSS

	Nivel KPSS
Estadística	0.540460035842587
P-valor	0.0325540459813994
Tamaño de la muestra	50
Hipótesis nula	La serie temporal es estacionaria
Hipótesis alternativa	La serie temporal tiene raíz unitaria

---