5. Pruebas de estacionalidad

Algunas series de tiempo exhiben un comportamiento conocido como estacionalidad. La estacionalidad de una serie temporal es el número de observaciones que toma la serie para repetir el patrón. En la herramienta “Pruebas de Estacionalidad”, es posible realizar dos pruebas para comprobar si la serie presenta estacionalidad.

Ejemplo:

Realizaremos la prueba con el siguiente conjunto de datos:

AMBV3
84.06
83.85
83.56
83.47
83.27
82.81
82.20
82.06
81.62
80.77
81.30
81.92
82.75
82.77
82.84
82.82
82.72
82.29
81.18
80.11
80.27
80.21
79.92
79.96
80.19
80.17
80.17
79.85
81.00
80.44
79.96
79.85
79.82
80.11
80.20
80.31
81.18
80.81
81.15
81.32
81.21
81.40
81.10
81.40
82.27
82.15
81.78
81.69
81.34
81.88

---

Subiremos los datos al sistema.

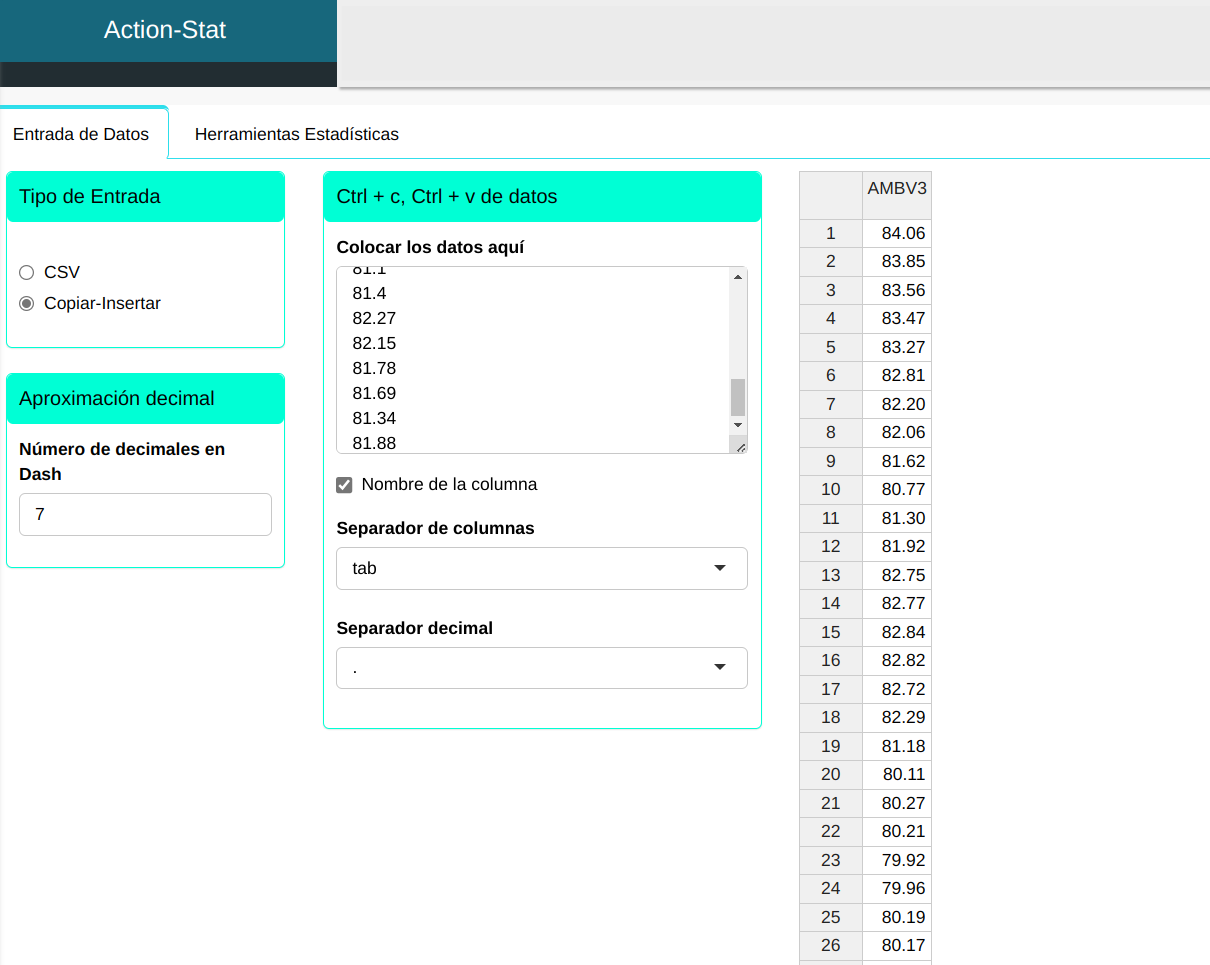
Realizaremos el análisis ajustando conforme la figura abajo.

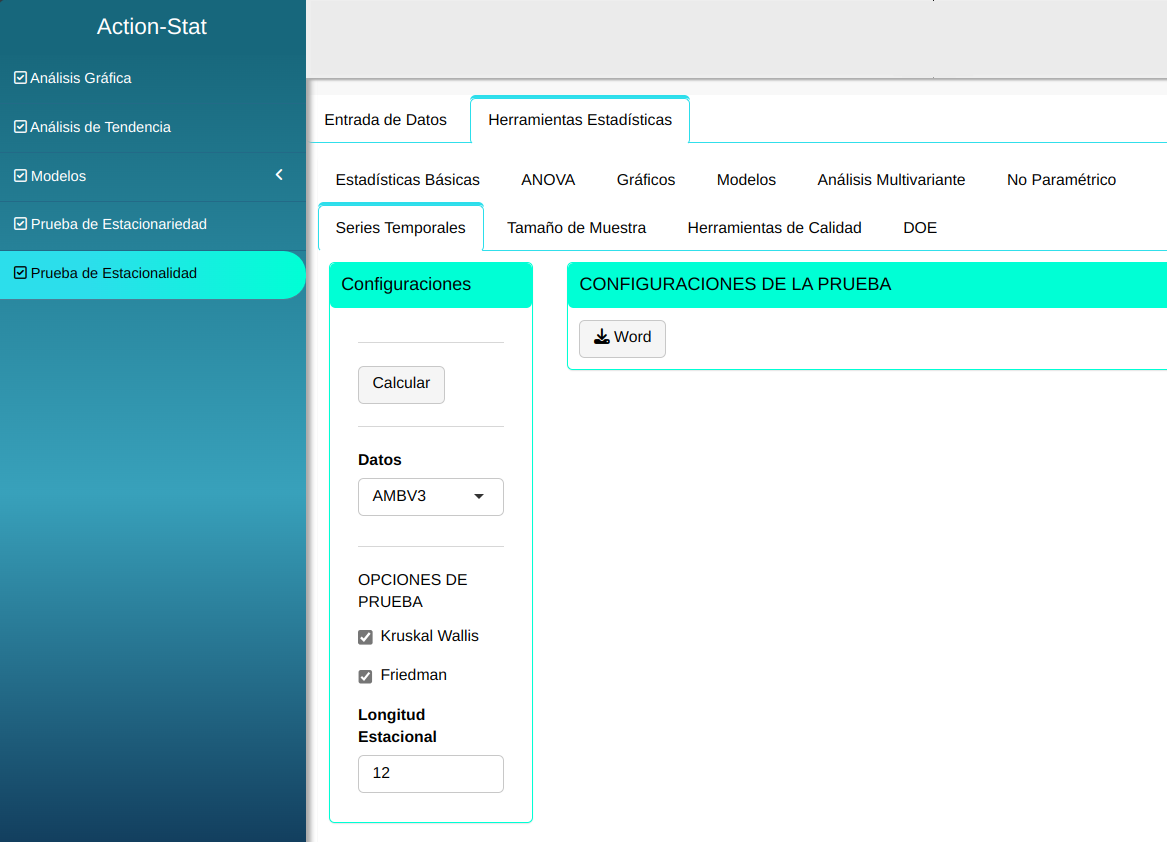
En seguida, haga un clic en calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.

Los resultados son:

Test of Kruskal-Wallis

	Kruskal-Wallis chi-squared
Estadística	28.0688775510204
P-valor	0.003159616205745
Tamaño de la Muestra	50
Longitud Estacional	12
Hipótesis Nula	No hay estacionalidad determinista
Hipótesis Alternativa	Hay estacionalidad determinista

---

Test of Friedman

	Friedman Chi-squared
Estadística	24.6153846153846
P-valor	0.0103740819044975
Tamaño de la muestra	50
Longitud Estacional	12
Hipótesis Nula	No hay estacionalidad determinista
Hipótesis Alternativa	Hay estacionalidad determinista

---