2. Intervalo de Confianza
A partir de los datos del intervalo de confianza es posible obtener el tamaño muestral de la población para la media y la proporción.
Ejemplo 1:
Supongamos que una pequeña muestra piloto de n=10, extraída de una población, proporcionó los valores $\overline{x}$=15 y $s^2$ =16. ¿Cuál es el tamaño muestral necesario para estimar la media poblacional $\mu$ con un error de muestreo no superior a 0.5 y un nivel de confianza 1- $\alpha$ =0.95?
Luego calcularemos el tamaño de la muestra considerando lo siguiente valores.
| Desviación Estándar - s | Nivel de Significancia | Error Máximo de Muestreo |
| $\quad\qquad$ 4 | $\quad\qquad$ 0.05 | $\qquad\qquad$0.5 |
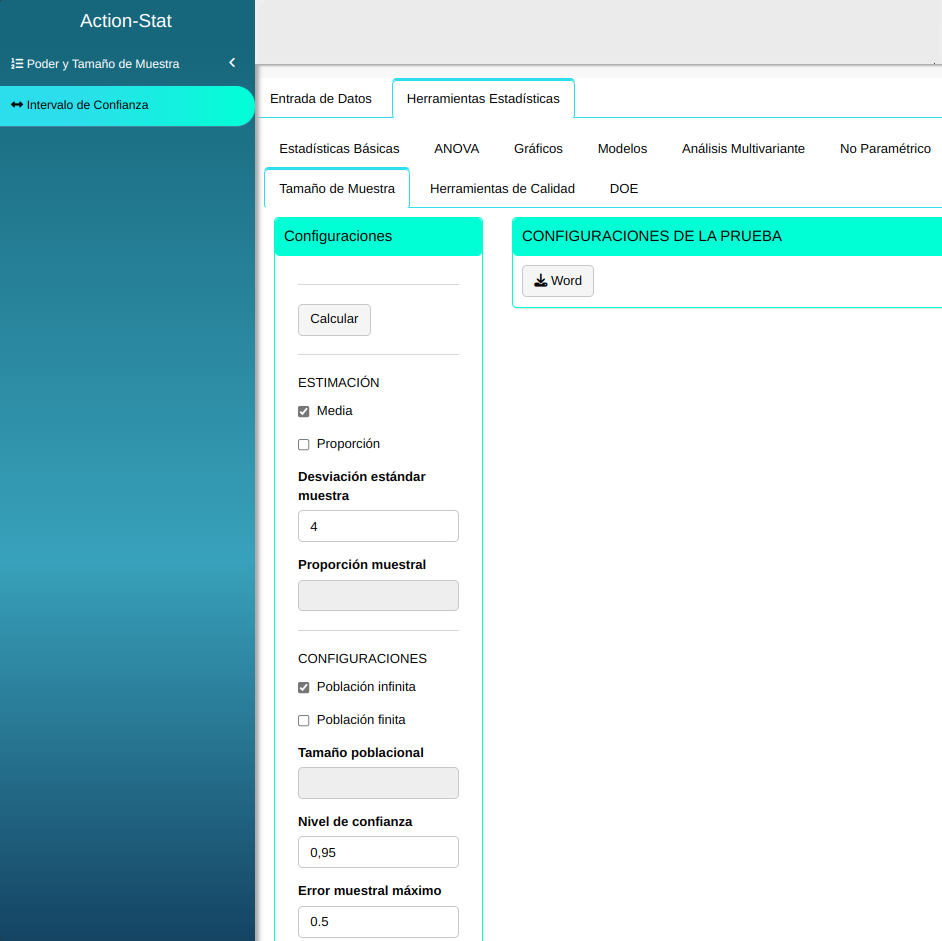
En seguida, haga un clic en Calcular para obtener los resultados e también se puede descargar los resultados en un archivo Word.
Los resultados son:
Cálculo del tamaño de la muestra
| tab | |
|---|---|
| Tamaño de la muestra | 246 |
| Error máximo de la muestra | 0.5 |
| Desviación Estándar de la Muestra | 4 |
| Tamaño de la Población | Inf. |
| Nivel de confianza | 0.95 |
Por lo tanto, podemos concluir que el tamaño de la muestra necesario para estimar la media de la población con un error de muestreo no superior a 0,5 y un nivel de confianza del 95% es de aproximadamente 246.
Ejemplo 2:
Supongamos que en un estudio de mercado se estima que el 60% de las personas entrevistadas prefieren la marca A de un analgésico. Esta información se basa en encuestas anteriores. Calcule el tamaño de la muestra para que el error de muestreo de $\hat{p}$ sea inferior al error de 0.03 y la confianza 1- $\alpha$ = 95%.
Luego calcularemos el tamaño de la muestra considerando los siguientes valores
| Proporción de la muestra | Nível de significancia | Erro máximo de la muestra |
| $\quad\qquad$ 0.6 | $\quad\qquad$ 0.05 | $\qquad\qquad$0.03 |
Para realizar el análisis lo configuramos como se muestra en la siguiente figura con los datos de la tabla.
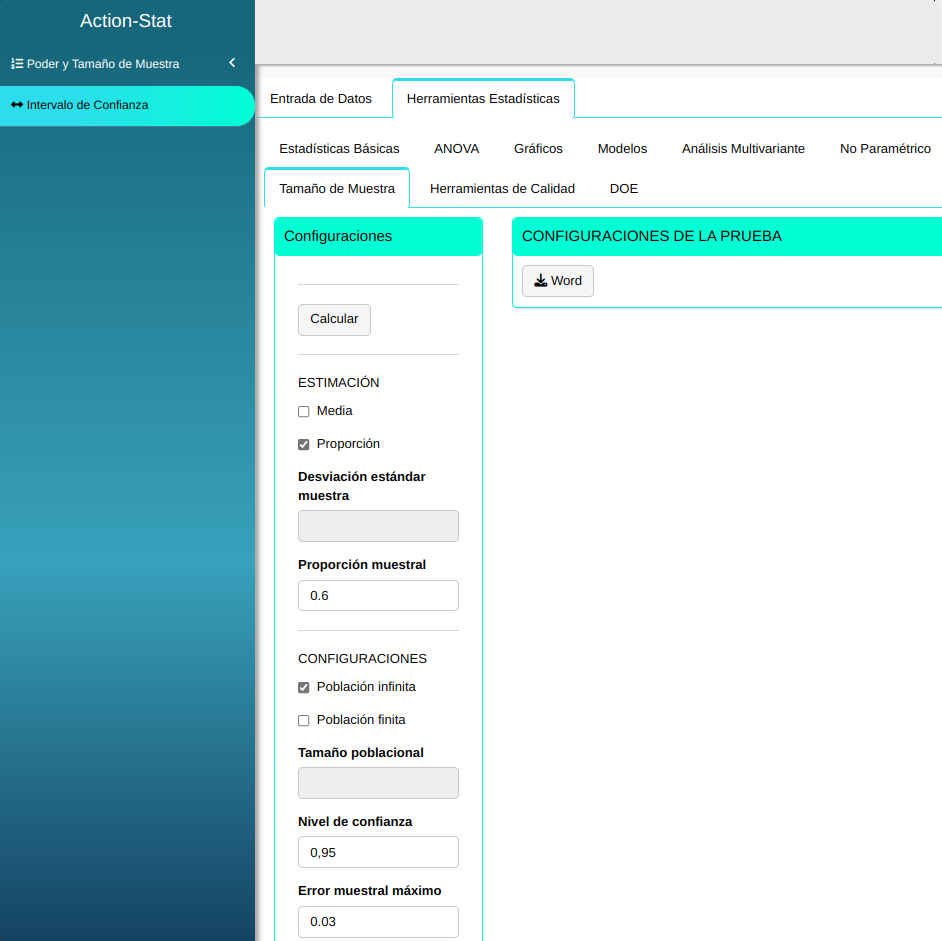
Haga clic en Calcular para ver los resultados y descargarlos en formato Word.
Los resultados son:
Cálculo del Tamaño de la Muestra
| tab | |
|---|---|
| Tamaño de la muestra | 1025 |
| Error máximo de la muestra | 0.03 |
| Proporción de la muestra | 0.6 |
| Tamaño de la población | Inf. |
| Nivel de confianza | 0.95 |
Por lo tanto, podemos concluir que el tamaño de la muestra necesario para estimar la proporción de la población con un error de muestreo no superior a 0.03 y un nivel de confianza del 95% es de aproximadamente 1025.