4. Anova
El análisis de varianza (ANOVA) es un método que se utiliza para comprobar si existen diferencias significativas entre las medias de grupos de datos. Se aplica con frecuencia en la investigación experimental para comparar los efectos de diferentes tratamientos. La prueba calcula el estadístico F, que corresponde a la razón entre la variación entre grupos y la variación dentro de los grupos.
Ejemplo 1:
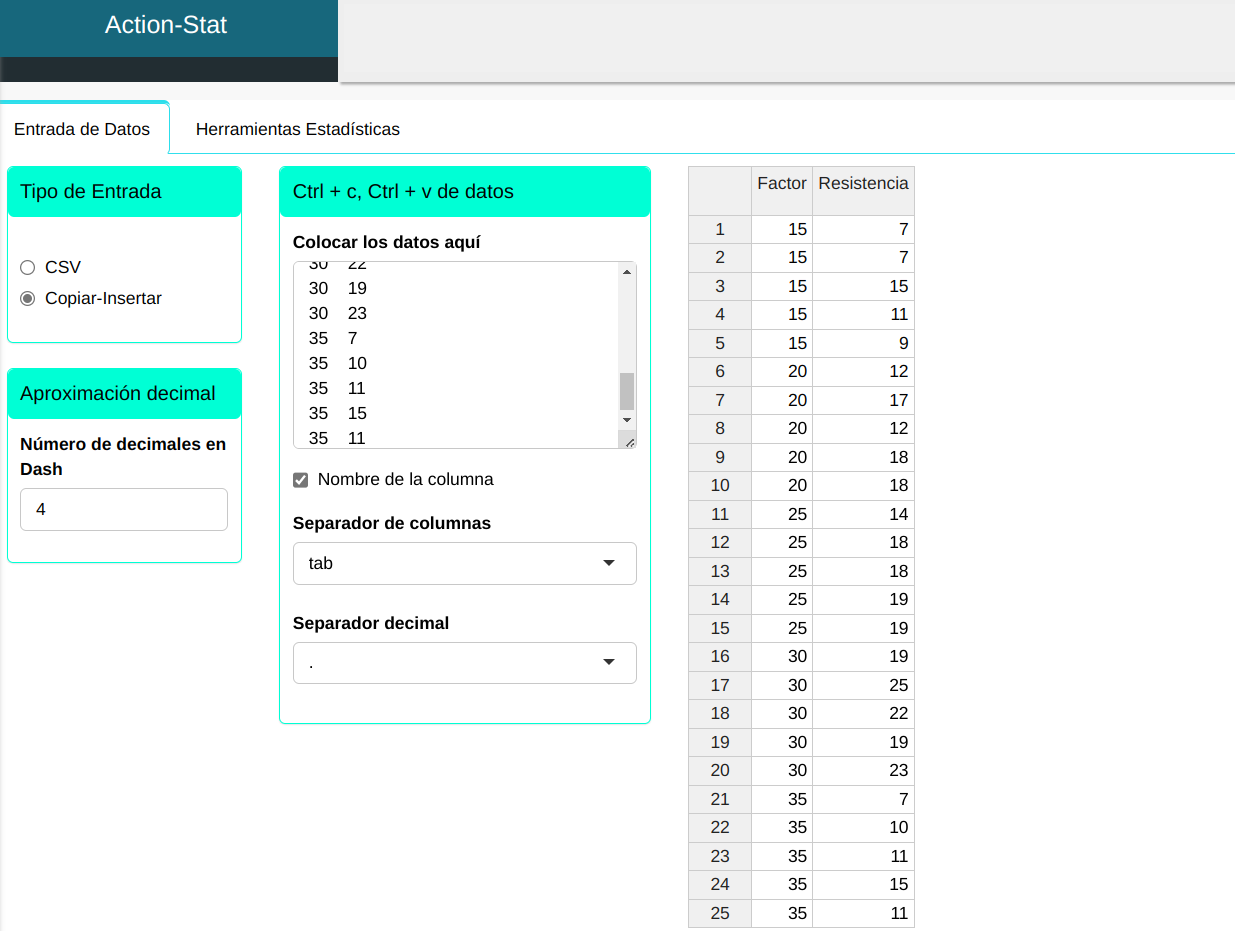
Consideremos el proceso de producción de una fibra sintética, en el que el experimentador desea conocer la influencia del porcentaje de algodón en la resistencia de la fibra. Para ello, se realiza un experimento completamente aleatorio en el que se evalúan diferentes niveles de porcentaje de algodón en relación con la resistencia de la fibra. Un punto importante en el montaje del experimento es que, para cada nivel de factor (porcentaje de algodón), los demás factores que influyen en el proceso deben mostrar un patrón homogéneo de variabilidad. En el experimento tomamos 5 niveles para el porcentaje de algodón y 5 repeticiones. Los valores están en cuadro a continuación:
| Factor | Resistencia |
|---|---|
| 15 | 7 |
| 15 | 7 |
| 15 | 1 |
| 15 | 11 |
| 15 | 9 |
| 20 | 12 |
| 20 | 17 |
| 20 | 12 |
| 20 | 18 |
| 20 | 18 |
| 25 | 14 |
| 25 | 18 |
| 25 | 18 |
| 25 | 19 |
| 25 | 19 |
| 30 | 19 |
| 30 | 25 |
| 30 | 22 |
| 30 | 19 |
| 30 | 23 |
| 35 | 7 |
| 35 | 10 |
| 35 | 11 |
| 35 | 15 |
| 35 | 11 |
| Número de niveles | Observación por nivel | Desviación estándar |
| $\quad\qquad$ 5 | $\quad\qquad$ 5 | $\quad$5.151698749 |
Subiremos los datos al sistema.
Para realizar la Anova, se realiza la siguiente configuración que se muestra en la figura siguiente.
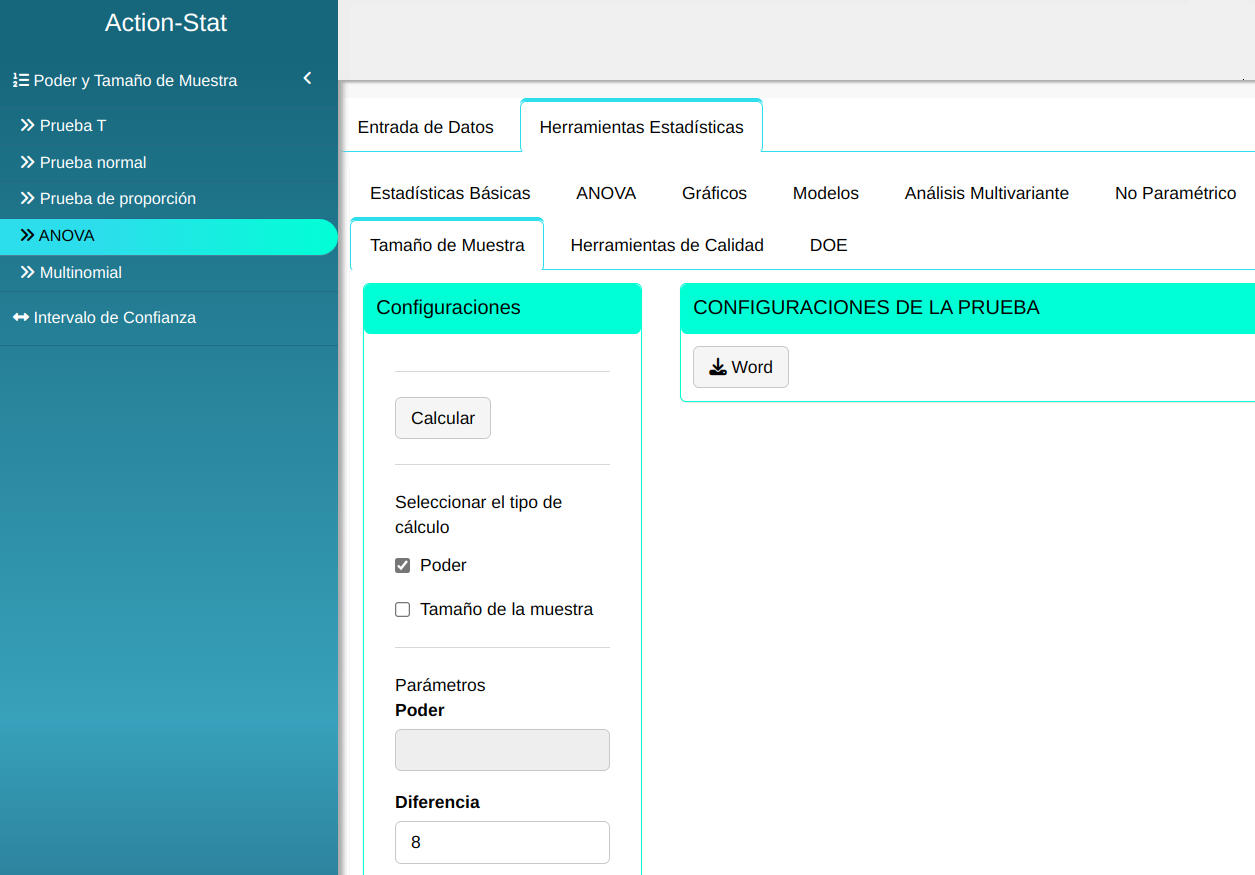
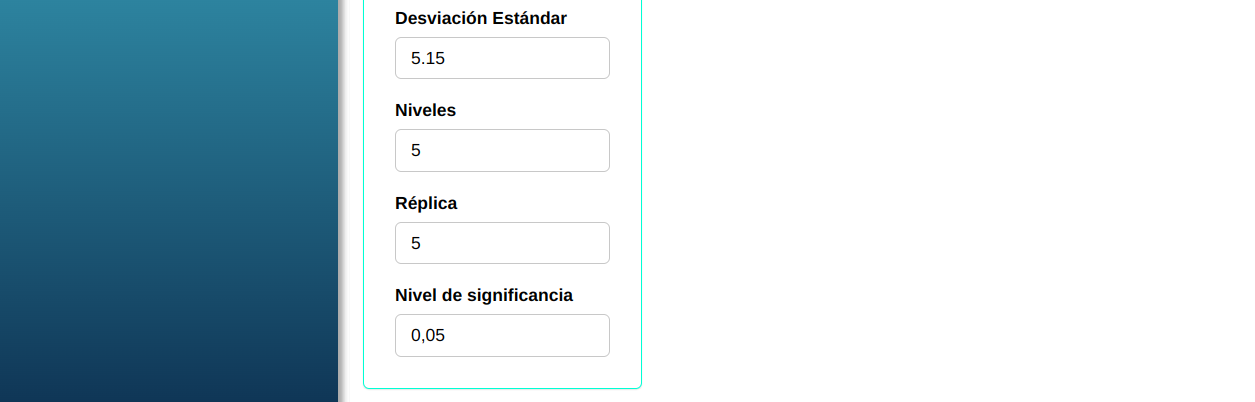
En seguida, haga un clic en Calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.
Los resultados son:
Potencia y tamaño de muestra - ANOVA
| V1 | |
|---|---|
| Poder | 0.3812579 |
| Niveles | 5.0000000 |
| Réplica | 5.0000000 |
| Diferencia | 8.0000000 |
| Desviación estándar | 5.1500000 |
| Nivel de significancia | 0.0500000 |
Entonces concluimos que para un nivel de significancia $\alpha$ = 0.05, la prueba tiene un poder de aproximadamente de 38.1%.
Ejemplo 2:
En el ejemplo anterior, calcule el número mínimo de réplicas para la prueba pueda detectar una diferencia $\Delta$ = 8 con ua poder de al menos 0.9.
Ajustamos conforme la figura abajo.
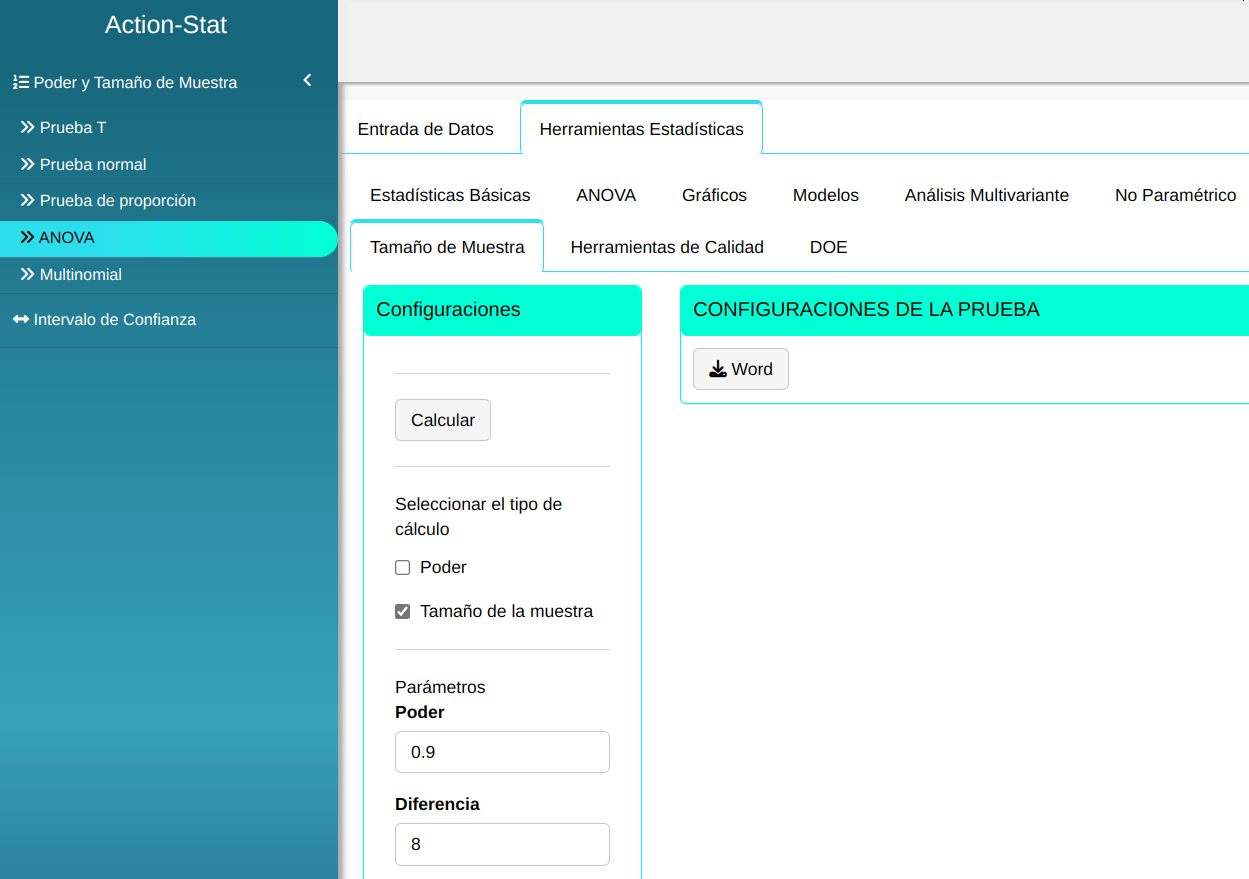
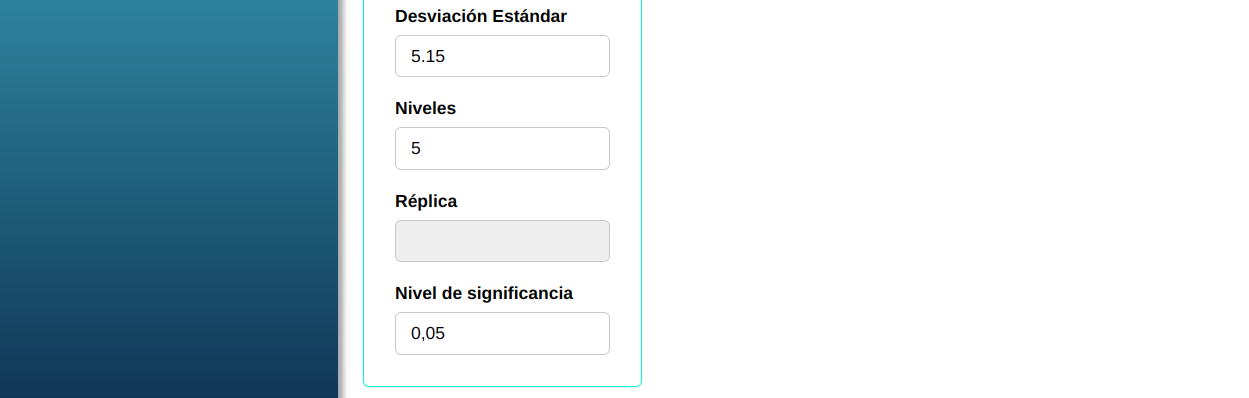
En seguida, haga un clic en Calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.
Los resultados son:
Potencia y tamaño de muestra - ANOVA
| V1 | |
|---|---|
| Poder | 0.90 |
| Niveles | 5.00 |
| Réplica | 14.00 |
| Diferencia | 8.00 |
| Desviación estándar | 5.15 |
| Nivel de significancia | 0.05 |
Entonces concluimos que se necesitan 14 repeticiones para que la prueba tenga un poder del 90%.