5. Multinomial
Utilizando la prueba de Chi-Cuadrado calculamos el poder del test de hipótesis o el tamaño de muestra necesario para tener un determinado poder para el test.
Ejemplo 1:
Un fabricante garantiza que el 90% de las piezas que suministra a la línea de producción de una determinada fábrica cumple las especificaciones exigidas. El análisis de una muestra de 200 piezas reveló que 25 estaban defectuosas. A un nivel del 5%, calcule el poder del test para detectar la diferencia entre la proporción nula de 0.9 y una posible proporción verdadera de 0.8.
Usaremos los datos de la siguiente tabla.
| n | $\mathbf{p_0}$ | $\mathbf{p_1}$ | $\mathbf{\alpha}$ |
| 200 | (0.9;0,1) | (0.8;0.2) | 0.05 |
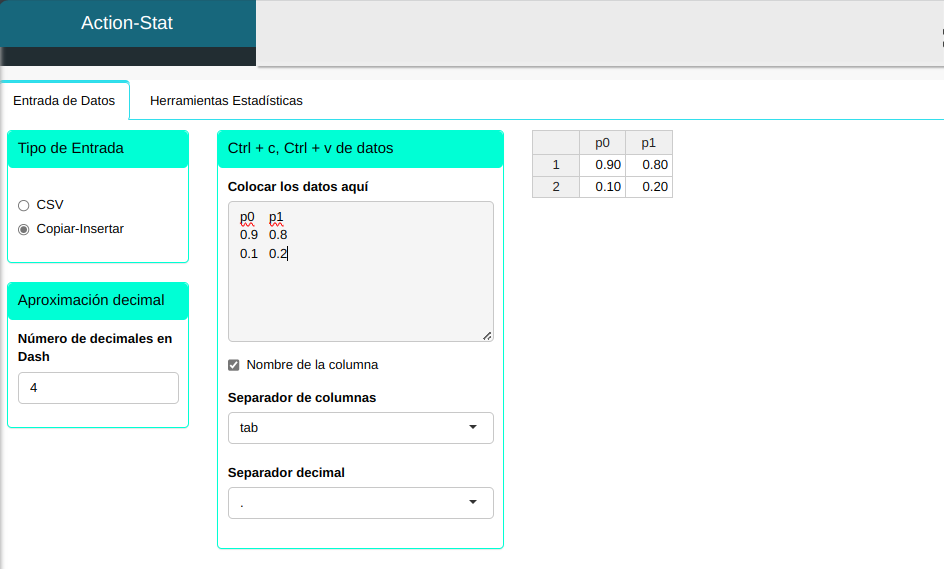
Subiremos los datos al sistema.
| p0 | p1 |
|---|---|
| 0.9 | 0.8 |
| 0.1 | 0.2 |
Ajustamos conforme la figura de abajo.
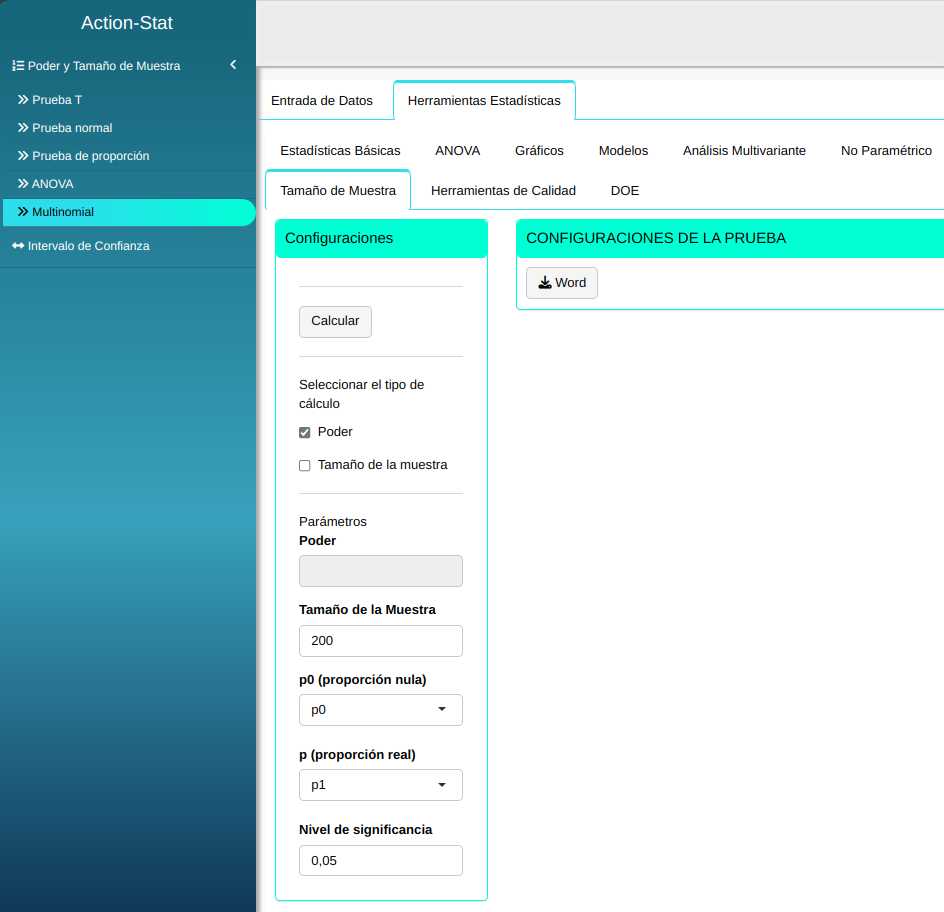
Damos un clic en Calcular y obtenemos los resultados. Los resultados también puden ser descargados en un archivo Word.
Resultado del análisis
| Aviso | |
| Poder | 0.9970571 |
| Tamaño de la muestra | 200 |
| p0 | 0.9 0.1 |
| p | 0.8 0.2 |
| Nivel de significancia | 0.05 |
Con esto, concluimos que el poder del test para detectar la diferencia entre la proporción nula de 0,9 y una posible proporción verdadera de 0,8 que es aproximadamente 99,71%.
Ejemplo 2:
Con un nivel de significancia del 5%, calcule el tamaño de muestra necesario para que la prueba de hipótesis detecte con una poder de al menos 0,9, una diferencia entre la proporción de la hipótesis nula $p_0$=0,9 y una posible proporción real $p$=0,87.
Usaremos los datos del siguiente cuadro:
| $\mathbf{p_0}$ | $\mathbf{p_1}$ | $\mathbf{\alpha}$ | Poder |
| (0.9;0,1) | (0.87;0.13) | 0.05 | 0.9 |
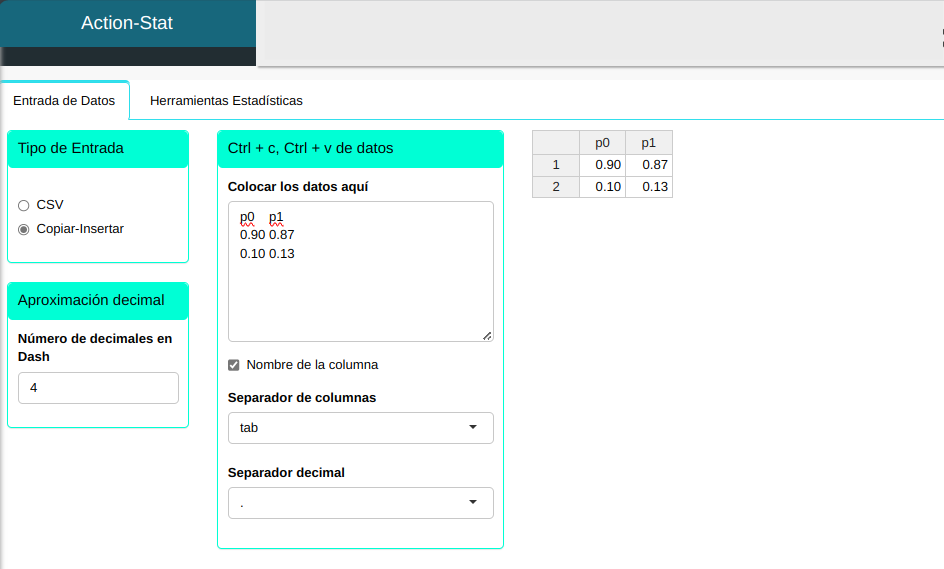
Subiremos los datos al sistema.
| p0 | p1 |
|---|---|
| 0.90 | 0.87 |
| 0.10 | 0.13 |
Ajustamos conforme la figura de abajo.
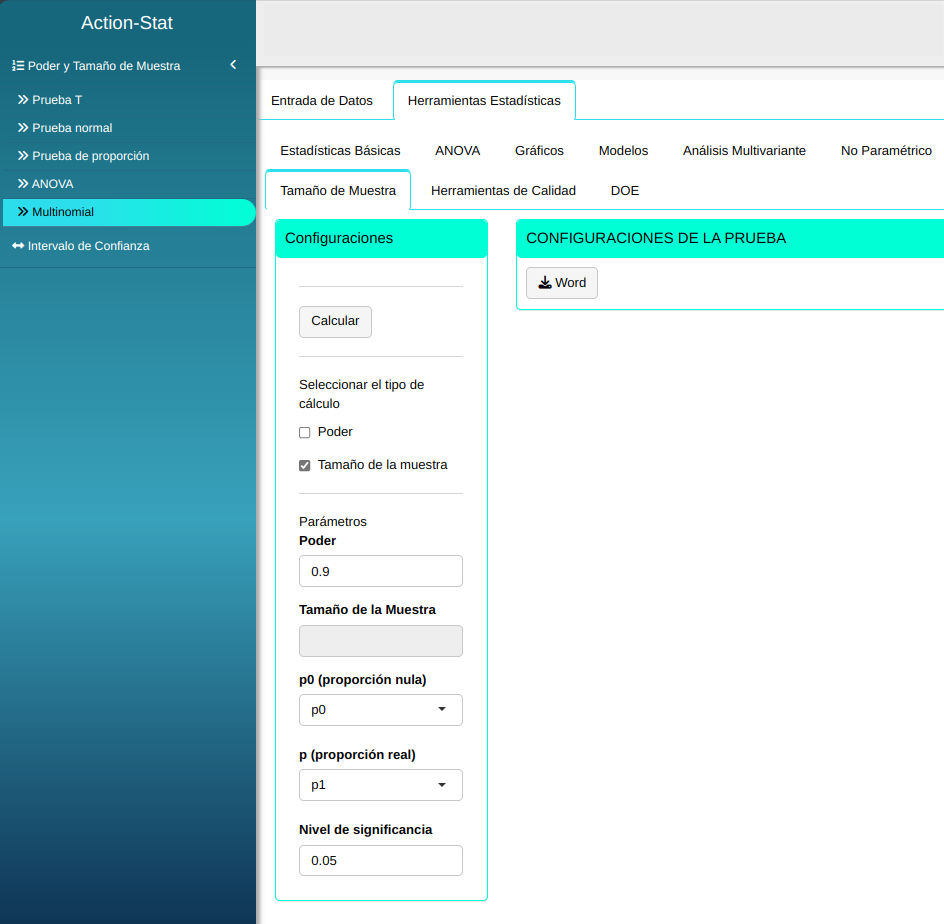
Damos un clic en Calcular y obtenemos los resultados. Los resultados también puden ser descargados en un archivo Word.
Resultado del análisis
| Aviso | |
| Poder | 0.9 |
| Tamaño de la muestra | 1051 |
| Proporción | 0.9 0.1 |
| Proporción hipotética | 0.87 0.13 |
| Nivel de significancia | 0.05 |
Por lo tanto concluimos que, para que la prueba detecte esta pequeña diferencia con un poder de al menos 0.9, se requiere un tamaño de muestra de al menos 1051.