3. Prueba de Proporción
Aquí se utiliza la prueba de una proporción para calcular el poder del test o el tamaño de la muestra.
Ejemplo 1:
Un fabricante garantiza que el 90% de las piezas que suministra a la línea de producción de una determinada fábrica cumple las especificaciones exigidas. El análisis de una muestra de 200 piezas reveló que 25 estaban defectuosas. Calcule el poder de la prueba para detectar la diferencia entre la proporción $p_0$ = 0.9 de la hipótesis nula y una proporción real $p$ = 0.8 a un nivel de 5 $%$ de significancia.
Usamos los datos del siguiente cuadro:
| $\mathbf{n}$ | $\mathbf{\alpha}$ | $\mathbf{p}$ | $\mathbf{p_0}$ |
| 200 | 0.05 | 0.8 | 0.9 |
Ajustamos conforme la figura de abajo.
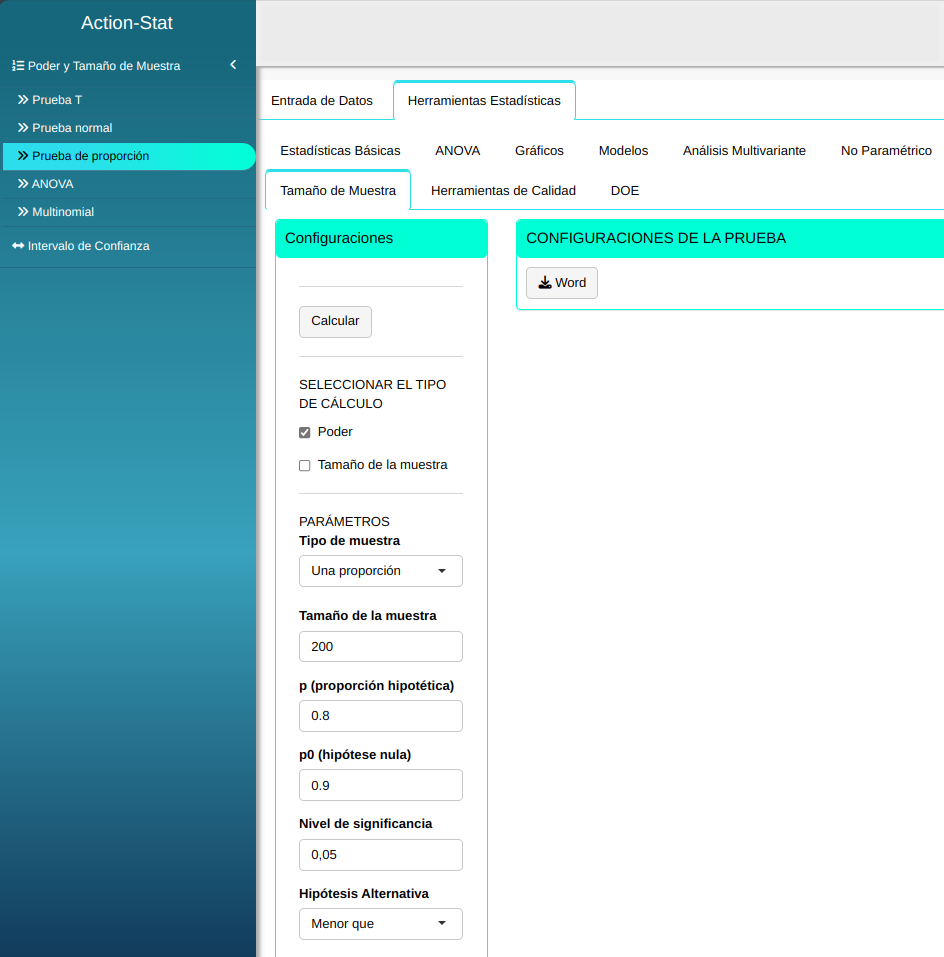
En seguida, haga un clic en calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.
Los resultados son:
Resultado del análisis
| Aviso | |
| Poder | 0.9910723 |
| Tamaño de la muestra | 200 |
| p | 0.8 |
| p0 | 0.9 |
| Nivel de significancia | 0.05 |
| Hipótesis alternativa | Menor que |
Con esto concluimos que la prueba tiene un poder aproximado al 99.1% para detectar una diferencia entre la proporción de la hipótesis nula $p_0$=0.9 y una posible proporción real $p$ = 0.8$.
Ejemplo 2:
Un fabricante garantiza que el 90 $%$ de las piezas que suministra a la línea de producción de una determinada fábrica se ajusta a las especificaciones requerido. El análisis de una muestra de 200 piezas reveló que 25 estaban defectuosas. Calcule el tamaño de muestra necesario para que la prueba tenga un poder de al menos 0.9 en la detección de la diferencia entre la proporción de la hipótesis nula $p_0$ = 0.9 y una posible proporción real de 0.85.
Usamos los datos de la siguiente tabla:
| $\mathbf{Poder}$ | $\mathbf{\alpha}$ | $\mathbf{p}$ | $\mathbf{p_0}$ |
| 0.9 | 0.05 | 0.85 | 0.9 |
Ajustamos conforme la figura de abajo.
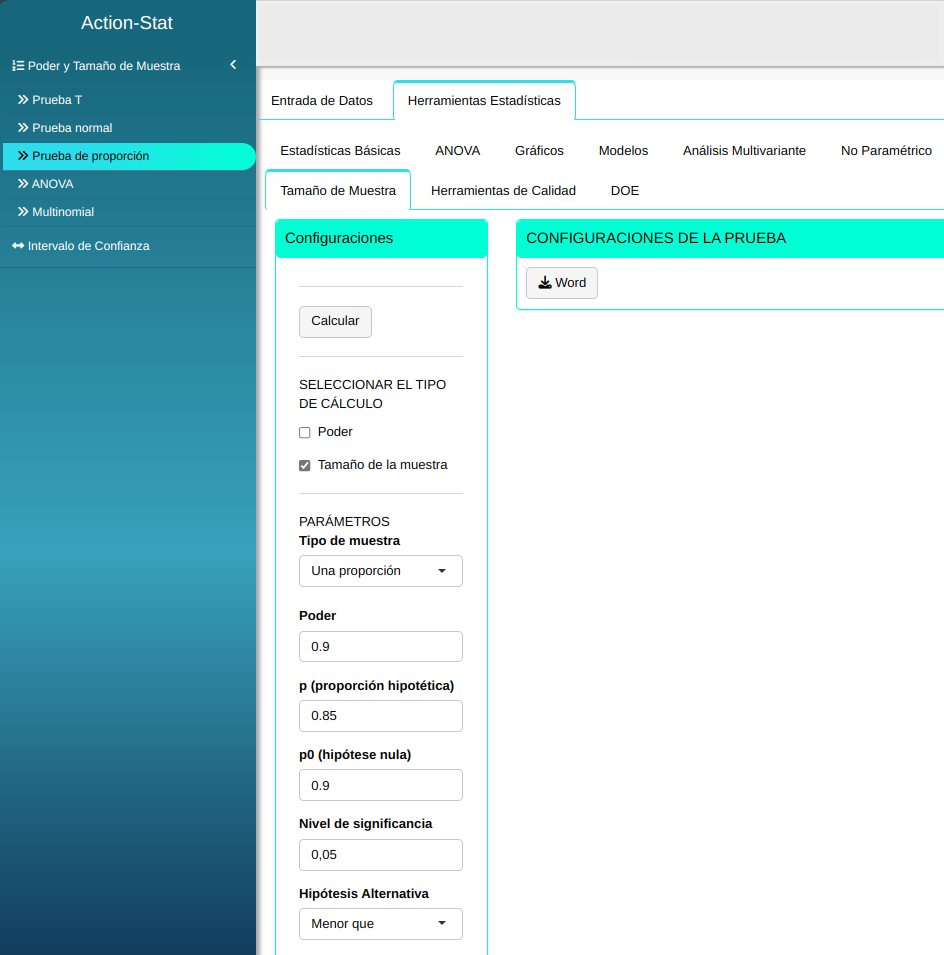
En seguida, haga un clic en calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.
Los resultados son:
Resultado del análisis
| Aviso | |
| Poder | 0.9 |
| Tamaño de la muestra | 372 |
| Proporción hipotética | 0.85 |
| Proporción | 0.9 |
| Nivel de significancia | 0.05 |
| Hipótesis alternativa | Menos de |
Ejemplo 3:
Dadas dos muestras de tamaños $n_1 = 100$, $n_2 = 100$, calcule el poder del test de dos proporciones para detectar las dos proporciones reales $p_1 = 0.88$ y $p_2 = 0.70$ para cada muestra con nivel de significancia $\alpha = 0.05$.
Usamos los datos del siguiente cuadro:
| $\mathbf{n_1}$ | $\mathbf{n_2}$ | $\mathbf{\alpha}$ | $\mathbf{p_1}$ | $\mathbf{p_2}$ |
| 100 | 100 | 0.05 | 0.88 | 0.70 |
Ajustamos conforme la figura de abajo.
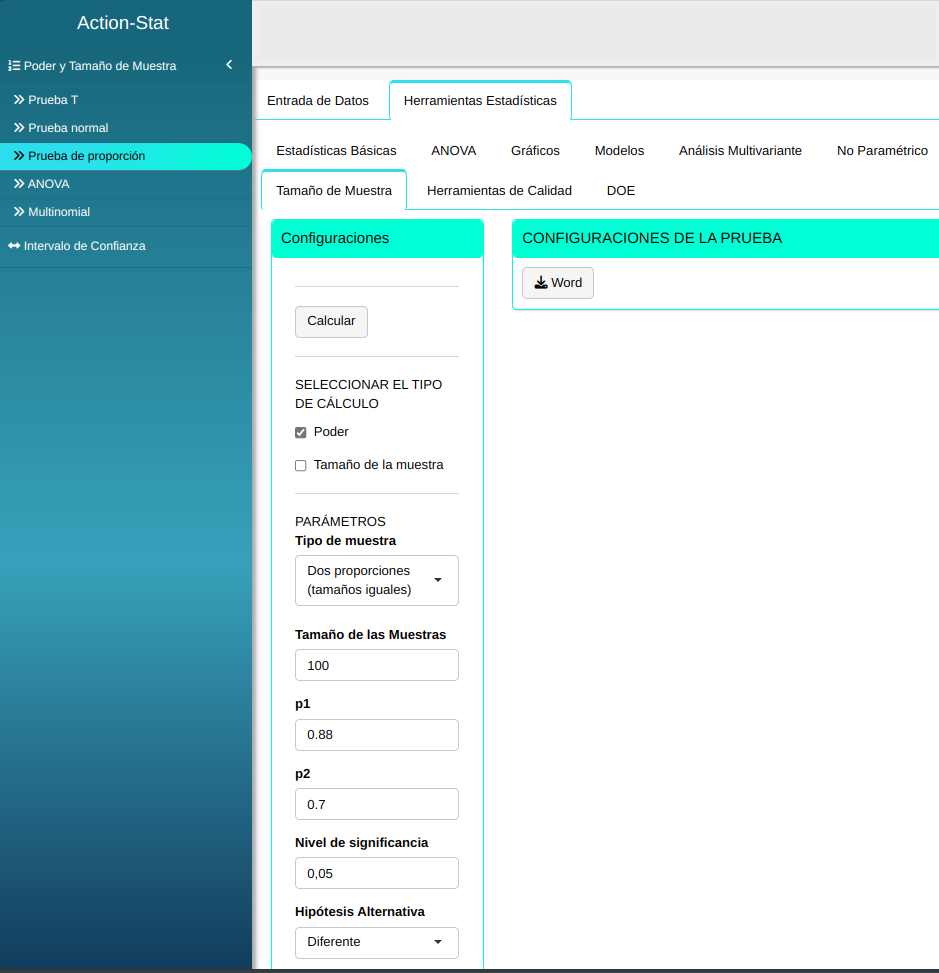
En seguida, haga un clic en calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.
Los resultados son:
Resultado del análisis
| Aviso | |
| Poder | 0.8915324 |
| Tamaño de la muestra | 100 |
| p1 | 0.88 |
| p2 | 0.7 |
| Nivel de significancia | 0.05 |
| Hipótesis alternativa | Diferente |
Ejemplo 4:
Calcule el tamaño de dos muestras para que la prueba de dos proporciones detecte las dos proporciones reales $p_1$ = 0.88 y $p_2$ = 0.80 con un poder de al menos 0.9 con nivel de significancia $\alpha$ = 0.05.
Utilice los datos del siguiente cuadro:
| $\mathbf{Poder}$ | $\mathbf{\alpha}$ | $\mathbf{p_1}$ | $\mathbf{p_2}$ |
| 0.9 | 0.05 | 0.88 | 0.80 |
Ajustamos conforme la figura de abajo.
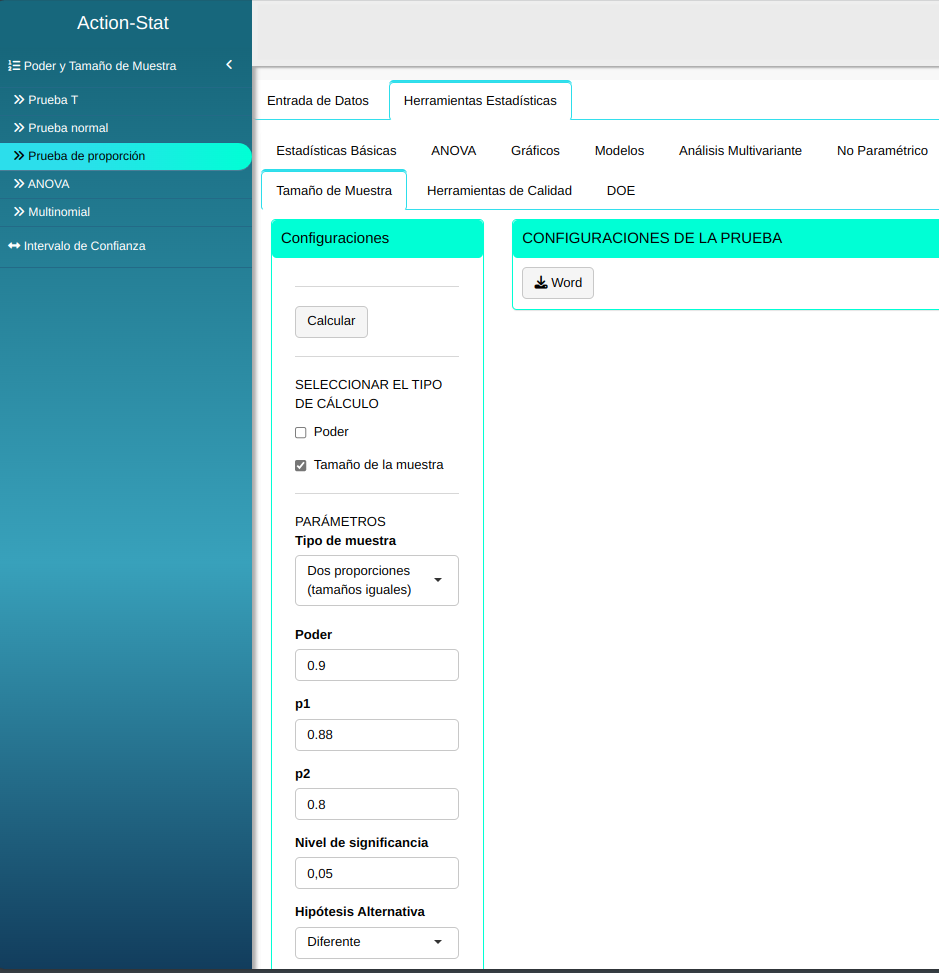
En seguida, haga un clic en calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.
Los resultados son:
Resultado del análisis:
| Aviso | |
| Poder | 0.9 |
| Tamaño de la muestra | 435 |
| p1 | 0.88 |
| p2 | 0.8 |
| Nivel de significancia | 0.05 |
| Hipótesis alternativa | Diferente |
Ejemplo 5:
Dadas dos muestras de tamaños $n_1$ = 100, $n_2$ = 120, calcule el poder del test de dos proporciones em detectar las dos proporciones reales $p_1$ = 0.88 y $p_2$ = 0.70 para cada muestra con nivel de significancia $\alpha$ = 0.05.
Usamos los datos del siguiente cuadro:
| $\mathbf{n_1}$ | $\mathbf{n_2}$ | $\mathbf{\alpha}$ | $\mathbf{p_1}$ | $p_2$ |
| 100 | 120 | 0.05 | 0.88 | 0.70 |
Ajustamos conforme la figura de abajo.
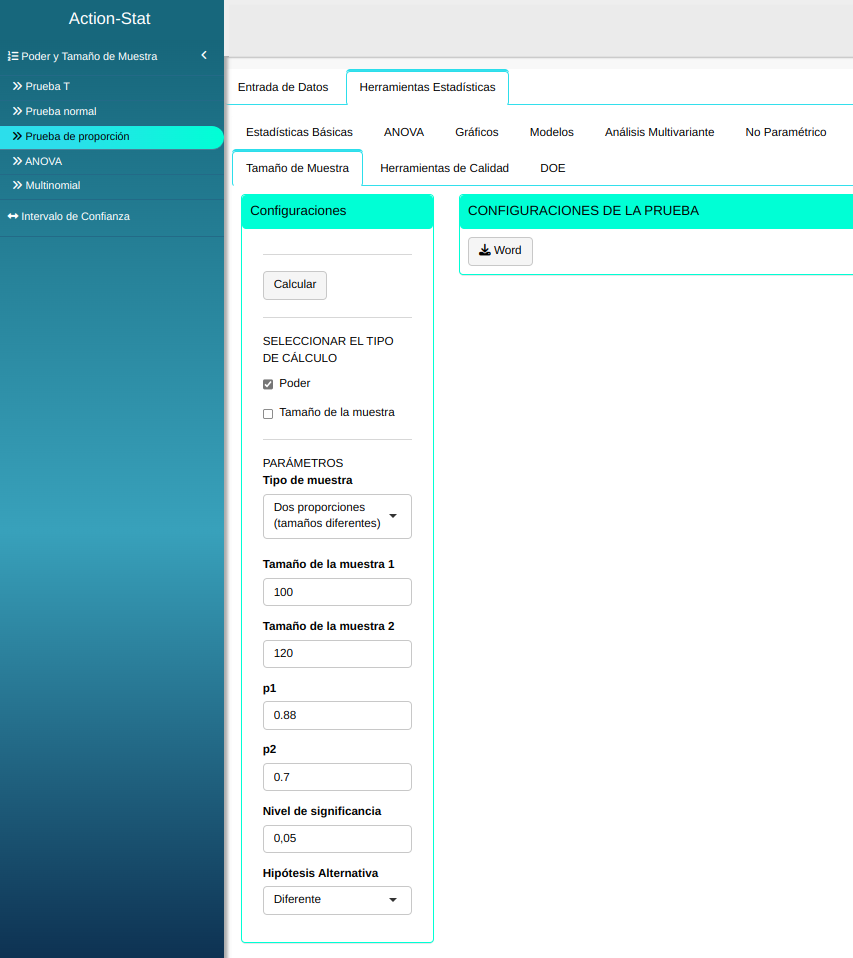
En seguida, haga un clic en calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.
Los resultados son:
Resultado del análisis
| Aviso | |
| Poder | 0.9157088 |
| Tamaño de muestra 1 | 100 |
| Tamaño de muestra 2 | 120 |
| p1 | 0.88 |
| p2 | 0.7 |
| Nivel de significancia | 0.05 |
| Hipótesis alternativa | Diferente |
Ejemplo 6:
Dado un tamaño de muestra de $n_1$ = 300, calcule el tamaño de la otra muestra para que la prueba de dos proporciones detecte las dos proporciones verdaderas $p_1$ = 0.88 y $p_2$ = 0.80 con un poder de al menos $0.9$, a un nivel de significancia $\alpha$ = 0.05.
Utilice los datos del siguiente cuadro:
| $\mathbf{Poder}$ | $\mathbf{\alpha}$ | $\mathbf{p_1}$ | $\mathbf{p_2}$ | $\mathbf{n_1}$ |
| 0.9 | 0.05 | 0.88 | 0.80 | 300 |
Ajustamos conforme la figura de abajo.
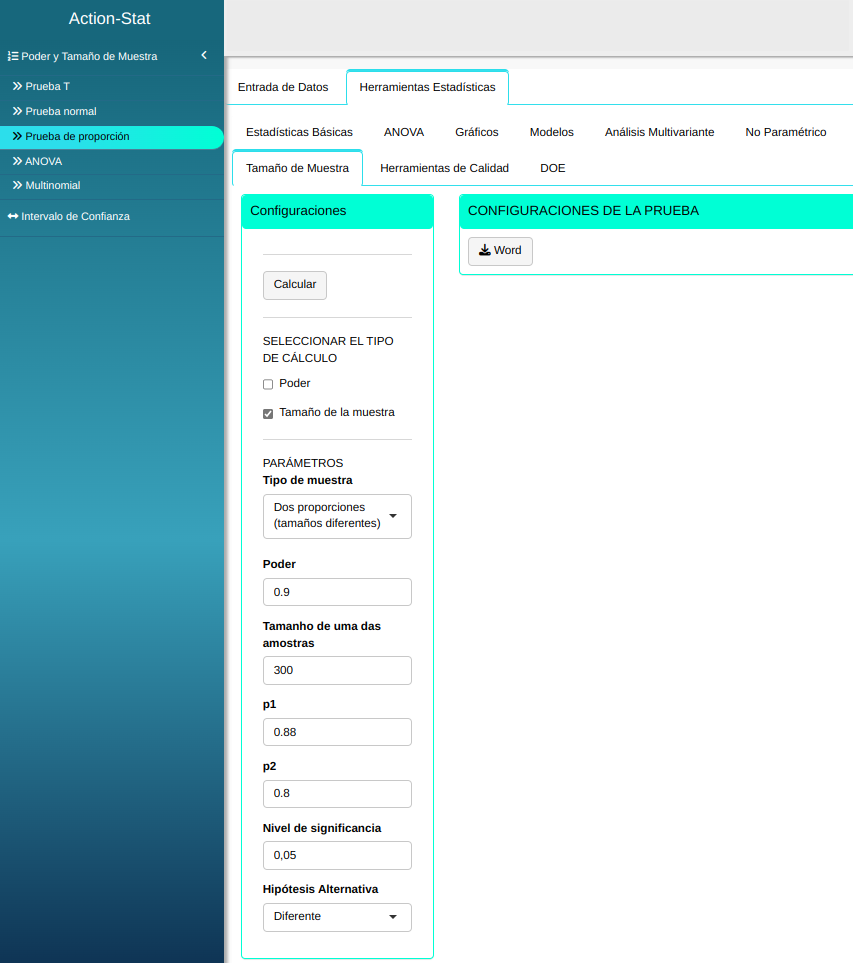
En seguida, haga un clic en calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.
Los resultados son:
Resultado del análisis
| Aviso | |
| Poder | 0.9 |
| Tamaño de la muestra 1 | 300 |
| Tamaño de la muestra 2 | 791 |
| p1 | 0.88 |
| p2 | 0.8 |
| Nivel de significancia | 0.05 |
| Hipótesis Alternativa | Diferente |