2. Prueba Normal
Aquí la Prueba Normal se utiliza para calcular la potencia de la prueba o la tamaño de la muestra.
Ejemplo 1:
Un supervisor de calidad quiere realizar una prueba basándose en una muestra aleatoria de tamaño $n = 35$ y para un nivel de significancia $\alpha = 0.05$, si la profundidad media de un agujero en una pieza determinada es de $72.4 mm$. ¿Cual es el poder del test para detectar una diferencia de $1.2$ entre la media real de la población y la media establecida por la hipótesis nula si sabemos por informaciones anteriores que $\sigma = 2.1mm$?
Primero establezcamos las hipótesis:
- $H_0$: $\mu = $ 72.4 mm
- $H_1$: $\mu\neq$ 72.4 mm
Para calcular el poder de esta prueba de hipótesis, usaremos los siguientes datos:
| $\mathbf{\sigma}$ | $\mathbf{n}$ | $\mathbf{\alpha}$ | diferença |
| 2.1 | 35 | 0.05 | 1.2 |
Ajustamos conforme la figura de abajo.
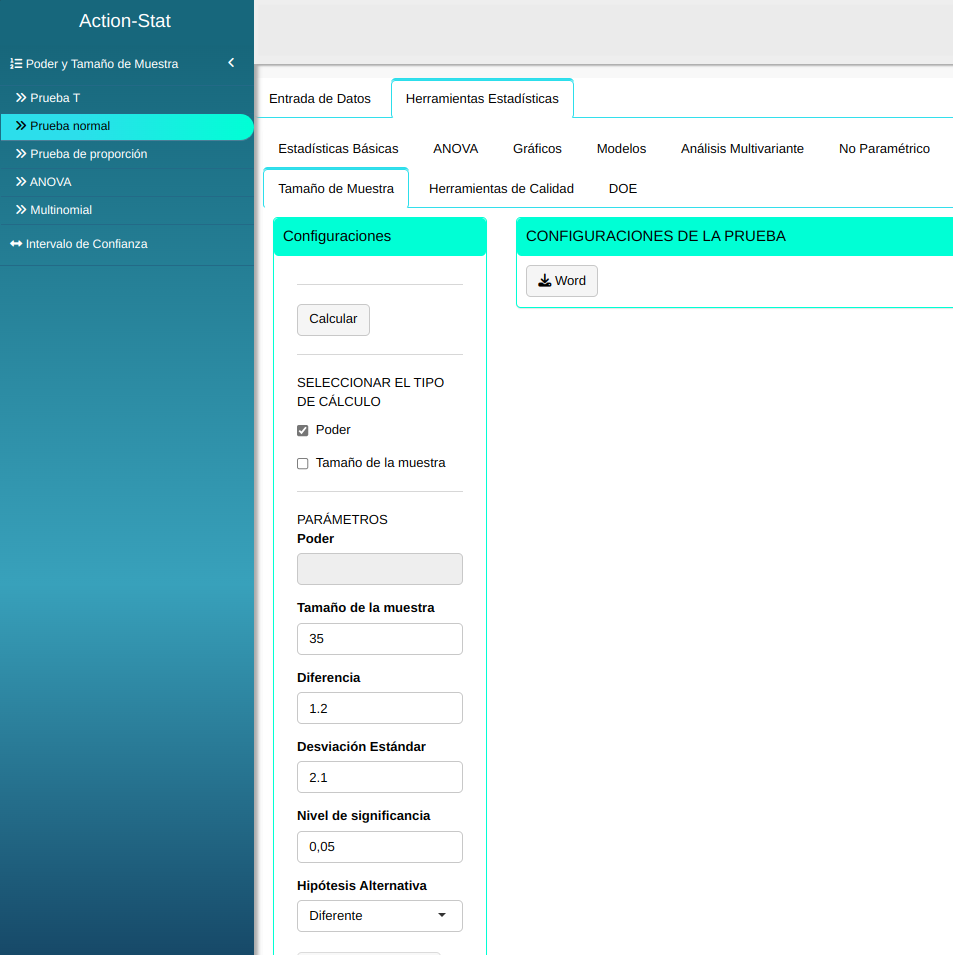
En seguida, haga un clic en calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.
Los resultados son:
Prueba normal
| V1 | |
|---|---|
| Poder | 0.9222912 |
| Tamaño de la muestra | 35 |
| Diferencia | 1.2 |
| Desviación estándar | 2.1 |
| Nivel de significancia | 0.05 |
| Hipótesis alternativa | Diferente |
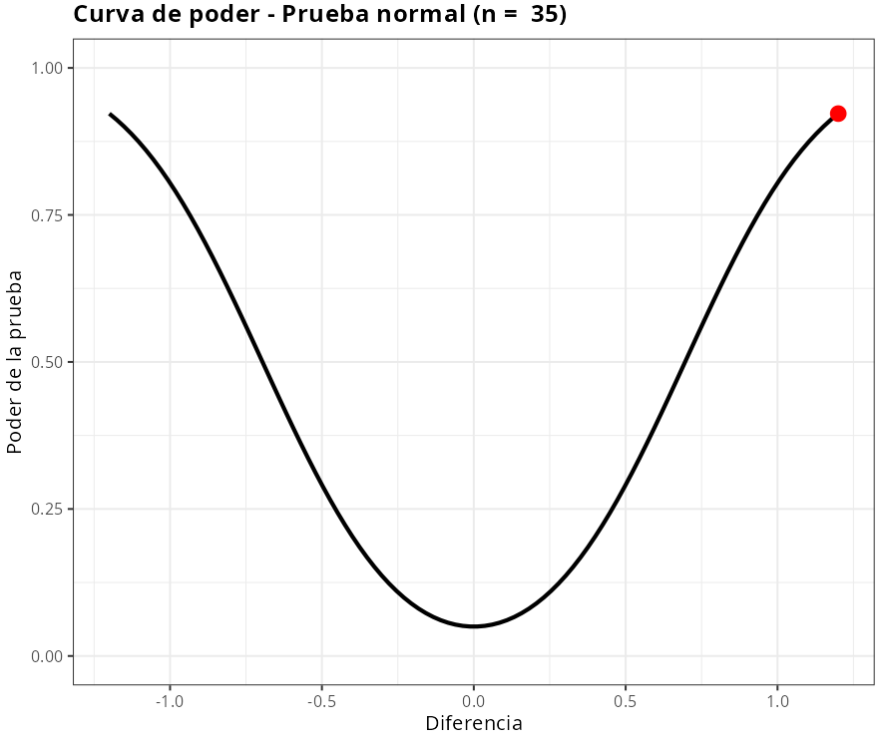
Con esto, concluimos que el poder del test de hipótesis para detectar una diferencia $d = 1.2$ entre el valor real de la media poblacional y el valor establecido por la hipótesis nula es aproximadamente del $92.23%$.
Ejemplo 2:
¿Cuál es el tamaño de muestra necesario para que, a un nivel de significancia $α = 0.05$, una prueba de hipótesis normal detecta una diferencia $d = 0.6$ entre la media poblacional y la media establecida por la hipótesis nula con un poder de al menos $0.9$ sabiendo por información previa que $\sigma = 2.1 mm$?
Primero establezcamos las hipótesis:
- $H_0$: $\mu = $ 72.4 mm
- $H_1$: $\mu \neq$ 72.4 mm
Usaremos los datos del siguiente cuadro:
| $\mathbf{\sigma}$ | Poder | $\mathbf{\alpha}$ | diferença |
| 2.1 | 0.9 | 0.05 | 0.6 |
Ajustamos conforme la figura de abajo.
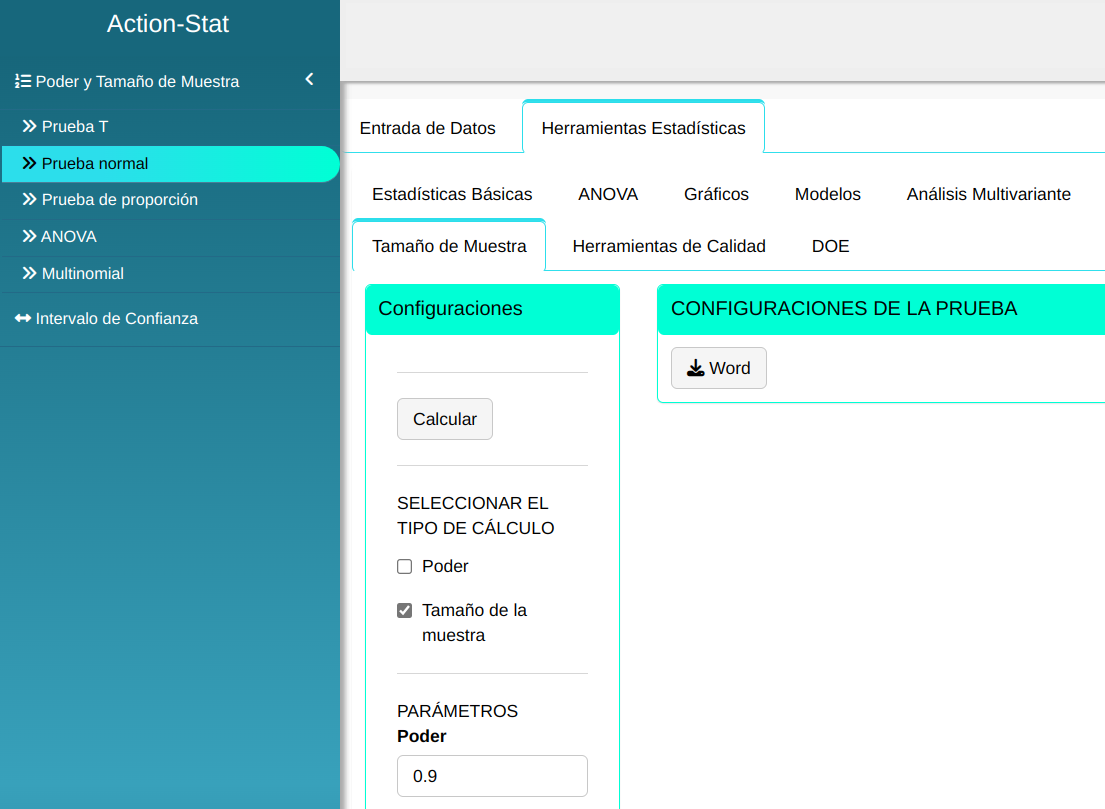
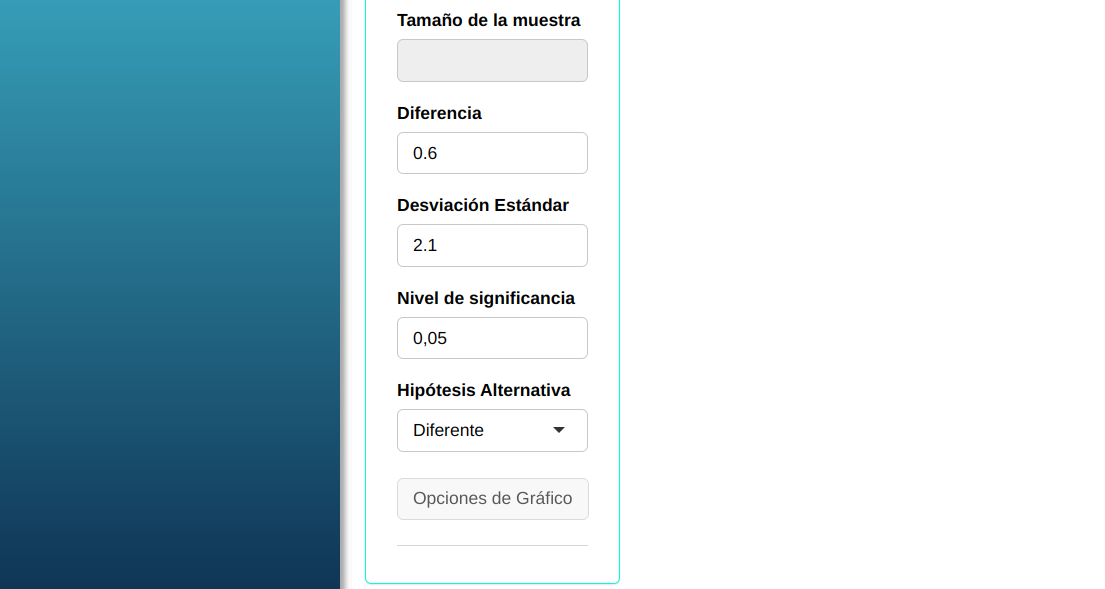
En seguida, haga un clic en calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.
Los resultados son:
Prueba normal
| V1 | |
|---|---|
| Poder | 0.9 |
| Tamaño de la muestra | 129 |
| Diferencia | 0.6 |
| Desviación estándar | 2.1 |
| Nivel de significancia | 0.05 |
| Hipótesis alternativa | Diferente |
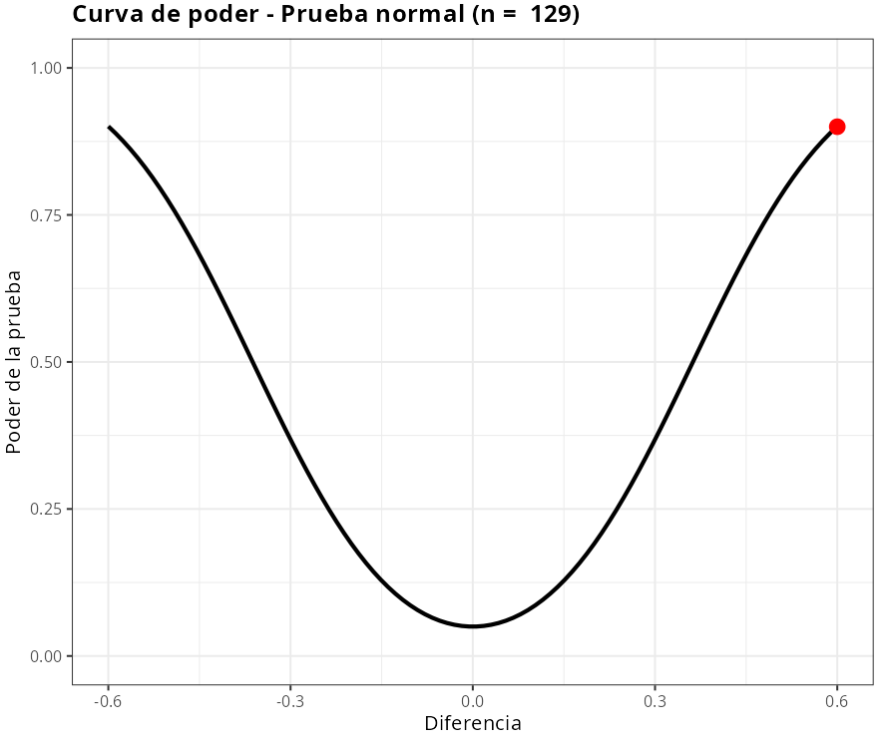
Por lo tanto, para que la prueba detecte una diferencia de 0.6 con un poder de, test al menos 0.9, se requiere un tamaño de muestra de 129 elementos.
Ejemplo 3:
El director de producción de una empresa tiene como objetivo evaluar la realización de una nueva metodología de enseñanza para nuevos trabajadores contratado. Con la metodología antigua, hay una tasa promedio de 4 errores. por trabajador en la primera semana de trabajo. En una muestra de 25 trabajadores, se aplicó la nueva metodología y se observó que el promedio fue de 5 errores por semana con una desviación estándar de 2. Con esta información calcular el poder del test para detectar una diferencia $d = 0.25$ entre los tasa verdadera y la tasa de la hipótesis nula con un nivel de significancia $\alpha = 0.05$.
Usaremos los datos del siguiente cuadro:
| $\mathbf{\sigma}$ | $\mathbf{n}$ | $\mathbf{\alpha}$ | diferença |
| 2 | 25 | 0.05 | 1 |
Ajustamos conforme la figura de abajo.
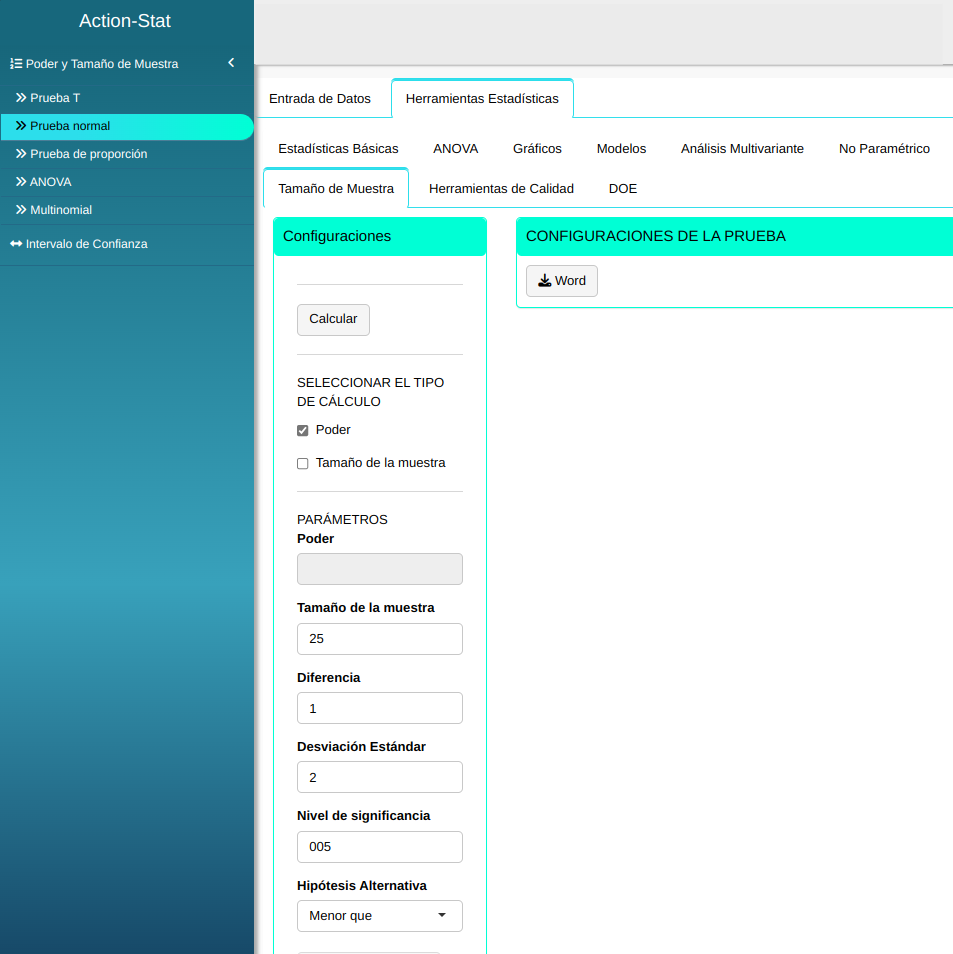
En seguida, haga un clic en calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.
Los resultados son:
Prueba normal
| V1 | |
|---|---|
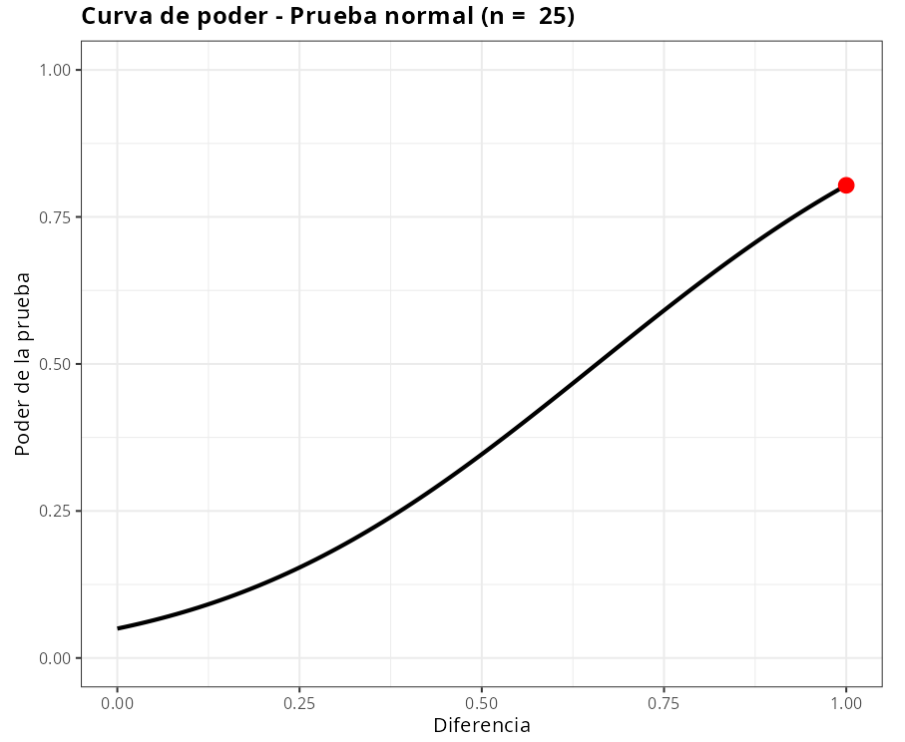
| Poder | 0.8037649 |
| Tamaño de la muestra | 25 |
| Diferencia | 1 |
| Desviación estándar | 2 |
| Nivel de significancia | 0.05 |
| Hipótesis alternativa | Mayor que |
Ejemplo 4:
El director de producción de una empresa tiene como objetivo evaluar la realización de una nueva metodología de enseñanza para nuevos trabajadores contratado. Con la metodología antigua, hay una tasa promedio de 4 errores por trabajador en la primera semana de trabajo. En una muestra de 25 trabajadores, se aplicó la nueva metodología y se observó que el promedio fue 5 errores por semana. Sabiendo que la desviación estándar es igual a 2, calcula el tamaño de muestra necesario para que la prueba detecte una diferencia $d = 0.25$ entre la tasa real y la tasa asumida por la hipótesis nula con potencia desde al menos $0.9$ hasta un nivel de significancia $\alpha$ = 0.05.
Utilice los datos del siguiente cuadro:
| $\mathbf{\sigma}$ | Poder | $\mathbf{\alpha}$ | diferença |
| 2 | 0.9 | 0.05 | 0.25 |
Ajustamos conforme la figura de abajo.
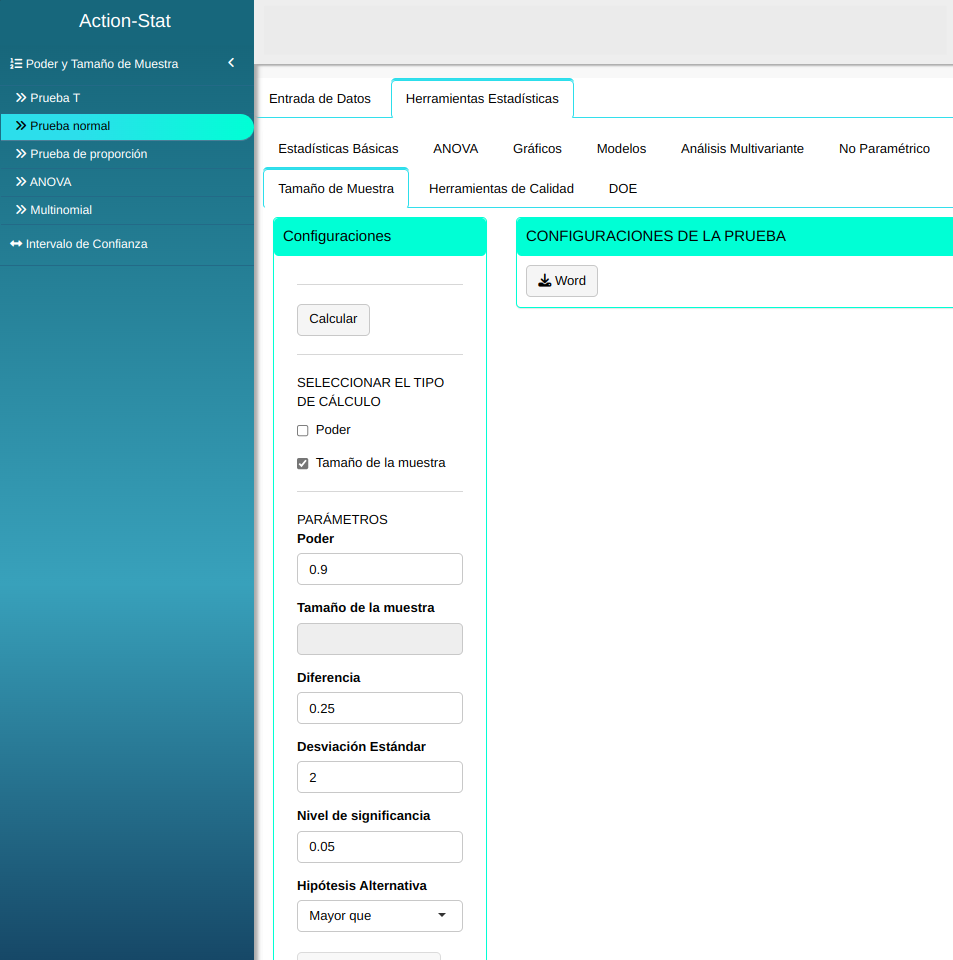
En seguida, haga un clic en calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.
Los resultados son:
Prueba normal
| V1 | |
|---|---|
| Poder | 0.9 |
| Tamaño de la muestra | 549 |
| Diferencia | 0.25 |
| Desviación estándar | 2 |
| Nivel de significancia | 0.05 |
| Hipótesis alternativa | Mayor que |
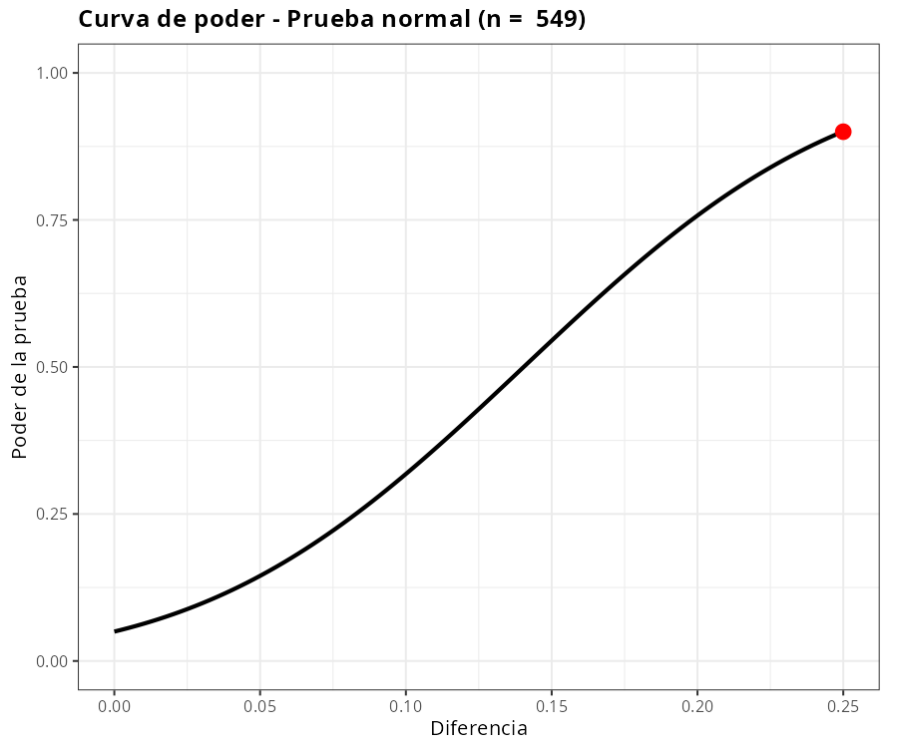
En otras palabras, para que la prueba detecte una diferencia $d = 0.25$ con un poder de test de al menos $0.9$, necesitamos tomar una muestra de $549$ elementos.