1. Prueba T
Aquí la prueba $T$ se utiliza para calcular el poder de la prueba de hipótesis o el tamaño de la muestra.
Ejemplo 1:
Un ingeniero de producción pretende comprobar, basándose en los datos de la siguiente tabla y con un nivel de significancia $\alpha$ = 0,05, si la altura media de una varilla se acerca al valor nominal de 1055 mm. Para ello, se analizó una muestra de 20 varillas, cuyas medidas se encuentran en la tabla.
| 903.88 |
| 1020.7 |
| 934.52 |
| 860.41 |
| 936.78 |
| 1036.92 |
| 915.38 |
| 1214.08 |
| 1039.19 |
| 1086.98 |
| 1098.04 |
| 1014.53 |
| 993.45 |
| 950.38 |
| 1144.94 |
| 1011.26 |
| 1097.79 |
| 1120.19 |
| 941.83 |
| 1066.12 |
En este caso establecemos las hipótesis
- $H_0$: $\mu =$ 1055
- $H_1$: $\mu \neq $ 1055
Usando la herramienta Resumen Descriptivo del menú Estadísticas Básicas de Action. tenemos que la media muestral es $\overline{X}=$ 1019.3685 y la desviación estándar de la muestra es $s = $ 91.36863255.
A continuación calcularemos el poder del test T considerando los siguientes valores
| $\quad\mathbf{\sigma}$ | $\mathbf{n}$ | nivel de significancia |
| 91.37 | 20 | $\qquad \quad$ 0.05 |
Para calcular el poder del test de hipótesis, calculamos la probabilidad de rechazar la hipótesis nula cuando en realidad es falsa, es decir, la hipótesis alternativa es verdadera. Así, suponemos un valor $x$ para la hipótesis alternativa y el poder del test es la probabilidad que tiene la prueba de detectar la diferencia d entre el valor $x$ de la hipótesis alternativa y el valor de la hipótesis nula.
Subiremos los datos al sistema.
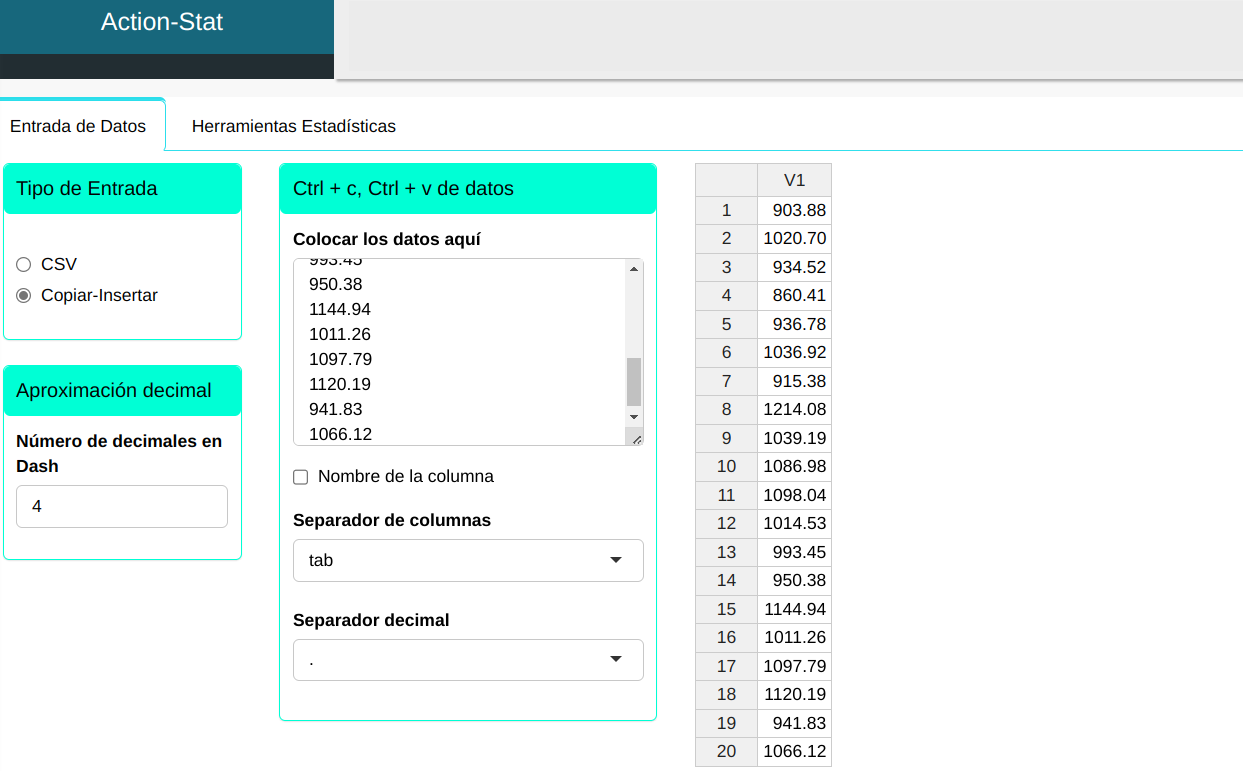
Para realizar el teste ajustamos conforme la figura de abajo.
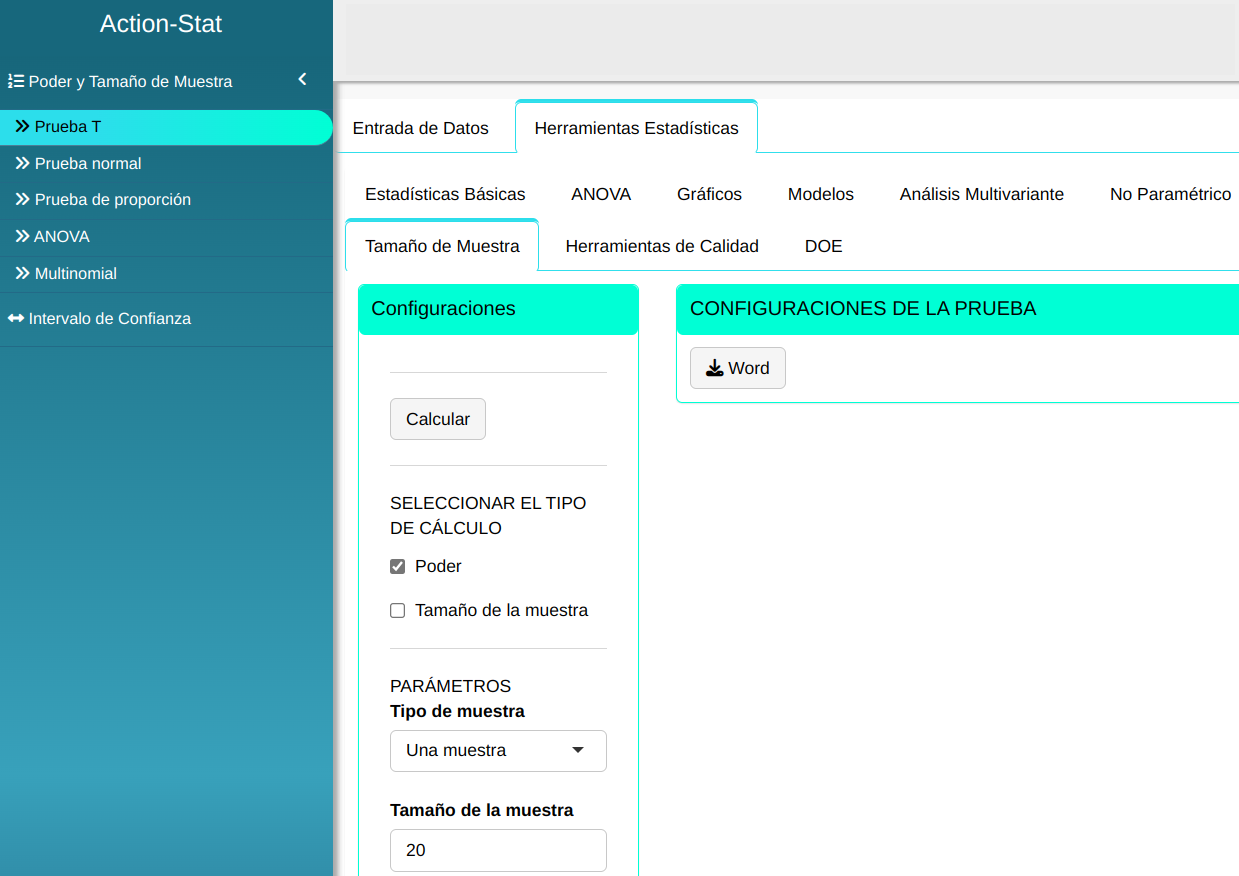
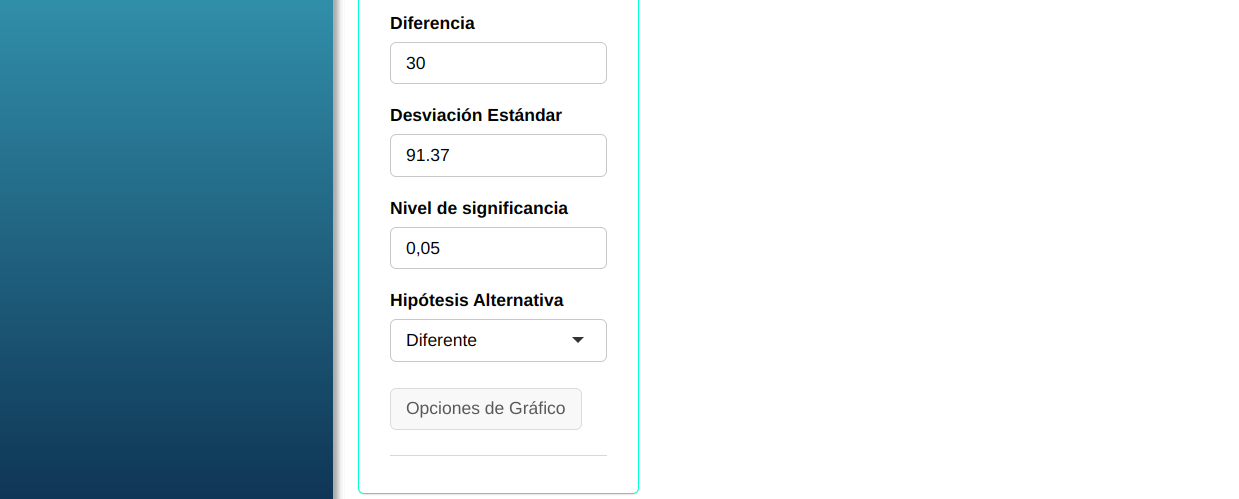
En seguida, haga un clic en calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.
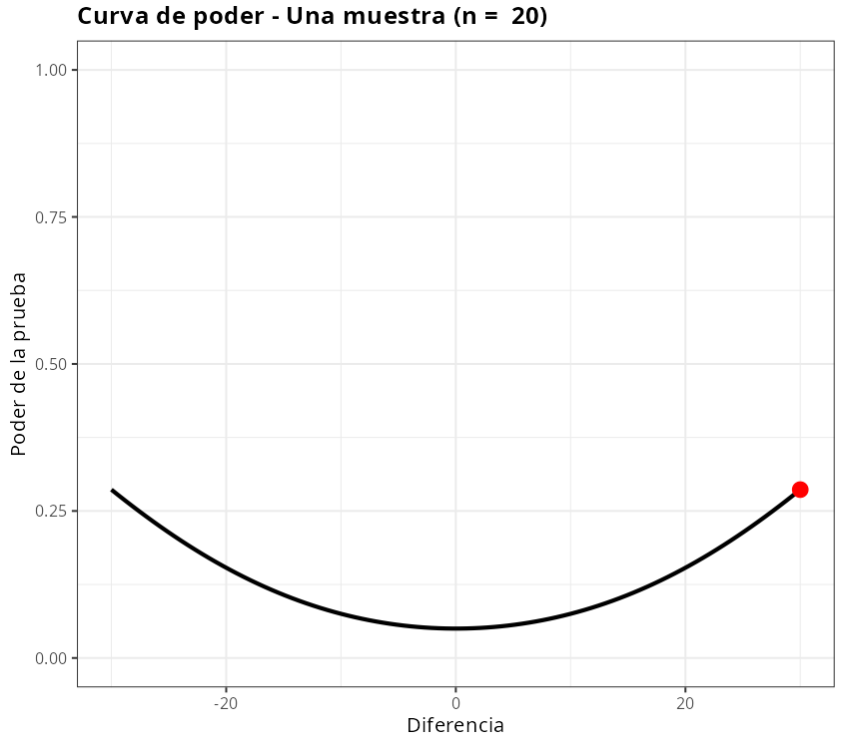
Los resultados son:
Prueba T: una muestra
| V1 | |
|---|---|
| Poder | 0.2863009 |
| Tamaño de la muestra | 20 |
| Diferencia | 30 |
| Nivel de significancia | 0.05 |
| Desviación estándar | 91.37 |
| Hipótesis alternativa | Diferente |
Ejemplo 2:
Utilizando los mismos datos del ejemplo anterior. supongamos ahora que desea calcular el tamaño de muestra necesario para que la prueba $T$ detecte una diferencia de 30mm con al menos 90% de poder.
| 903.88 |
| 1020.7 |
| 934.52 |
| 860.41 |
| 936.78 |
| 1036.92 |
| 915.38 |
| 1214.08 |
| 1039.19 |
| 1086.98 |
| 1098.04 |
| 1014.53 |
| 993.45 |
| 950.38 |
| 1144.94 |
| 1011.26 |
| 1097.79 |
| 1120.19 |
| 941.83 |
| 1066.12 |
Ajustamos conforme la figura de abajo.
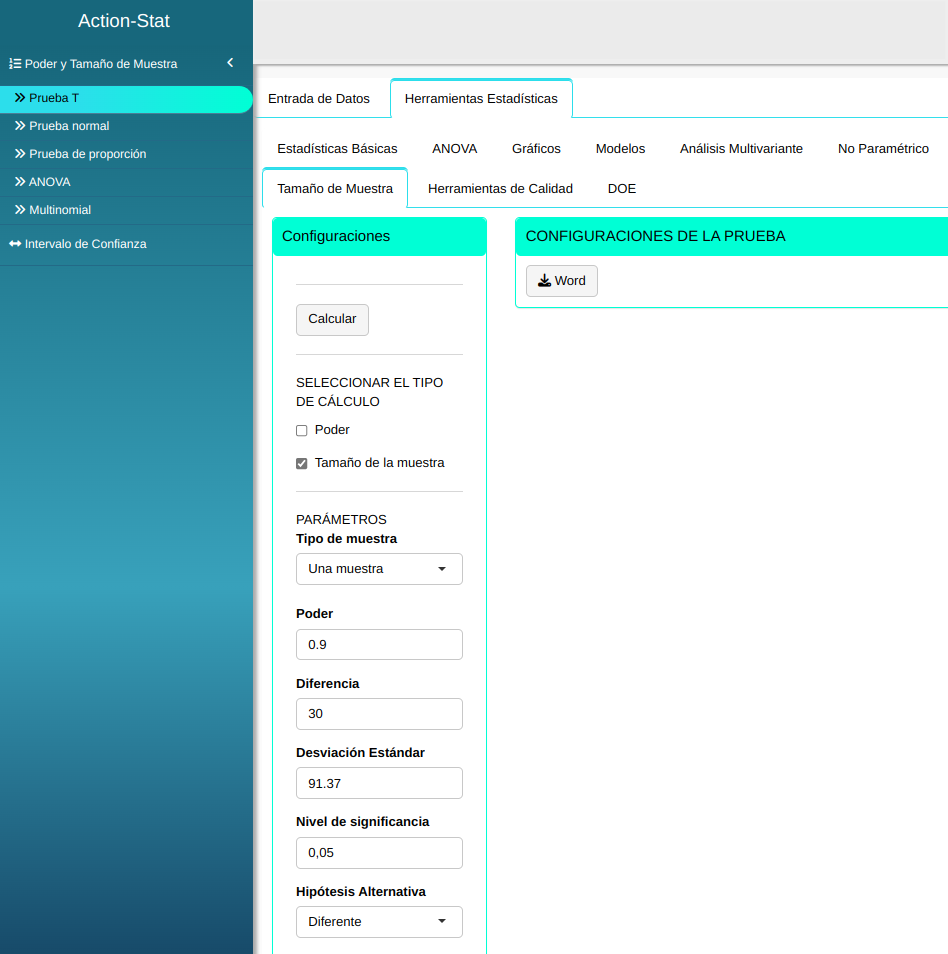
En seguida, haga un clic en calcular para obtener los resultados. También se puede descargar los resultados en un archivo Word.
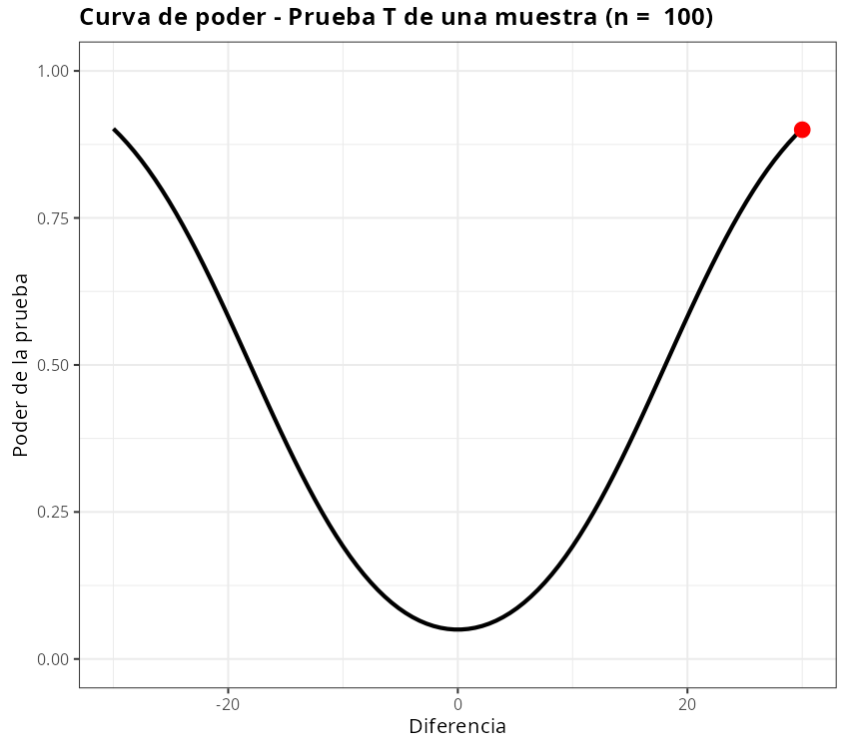
Los resultados son:
Prueba T: una muestra
| V1 | |
|---|---|
| Poder | 0.9 |
| Tamaño de la muestra | 100 |
| Diferencia | 30 |
| Nivel de significancia | 0.05 |
| Desviación Estándar | 91.37 |
| Hipótesis alternativa | Diferente |
Ejemplo 3:
Considerando los siguientes datos, compare las medias muestrales.
| Muestra 1 | Muestra 2 |
|---|---|
| 976.46 | 982.82 |
| 1106.84 | 949.61 |
| 107.73 | 1128.40 |
| 1022.91 | 1127.82 |
| 1102.38 | 960.57 |
| 930.62 | 967.27 |
| 1104.27 | 1095.48 |
| 1007.22 | 996.85 |
| 1114.63 | 1087.26 |
| 1093.14 | 1086.14 |
| 923.04 | 937.53 |
| 1044.95 | 1088.24 |
| 929.86 | 1018.75 |
| 1102.16 | 1131.13 |
| 919.15 | 949.66 |
| 962.61 | 1121.67 |
| 1039.07 | 953.73 |
| 1111.61 | 970.52 |
| 1044.90 | 952.71 |
| 1032.52 | 1066.47 |
| 1100.22 | 939.22 |
| 1100.82 | 1052.59 |
| 931.91 | 947.21 |
| 951.91 | 1086.75 |
| 1024.30 | 1124.85 |
Establecer las hipótesis:
- $H_0$: $\mu_1 - \mu_2 = $ 0
- $H_1$: $\mu_1 - \mu_2 \neq $ 0
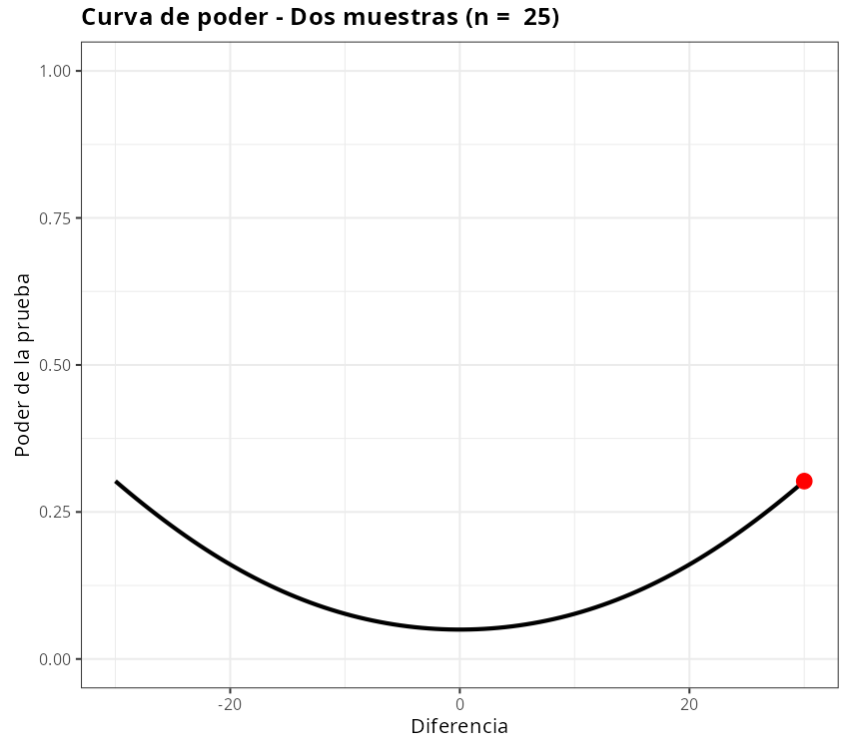
Calculemos el poder de la prueba T con dos muestras del mismo tamaño. Para detectar una diferencia $μ_1 - μ_2$ = 30, es necesario calcular la desviación estándar. Utilizando la herramienta “Resumen descriptivo” de Action. Obtenemos los valores $s_1$=70.54 y $s_2$=73.63.
| $\mathbf{n_1 = n_2}$ | $\mathbf{\alpha}$ | Diferença $\mathbf{(\mu_1 - \mu_2)}$ | Desvio-Padrão 1 | Desvio-Padrão 2 |
| $\quad$ 25 | 0.05 | $\qquad$ 30 | $\quad \quad$ 70.54 | $\qquad$ 73.63 |
Subiremos los datos al sistema.
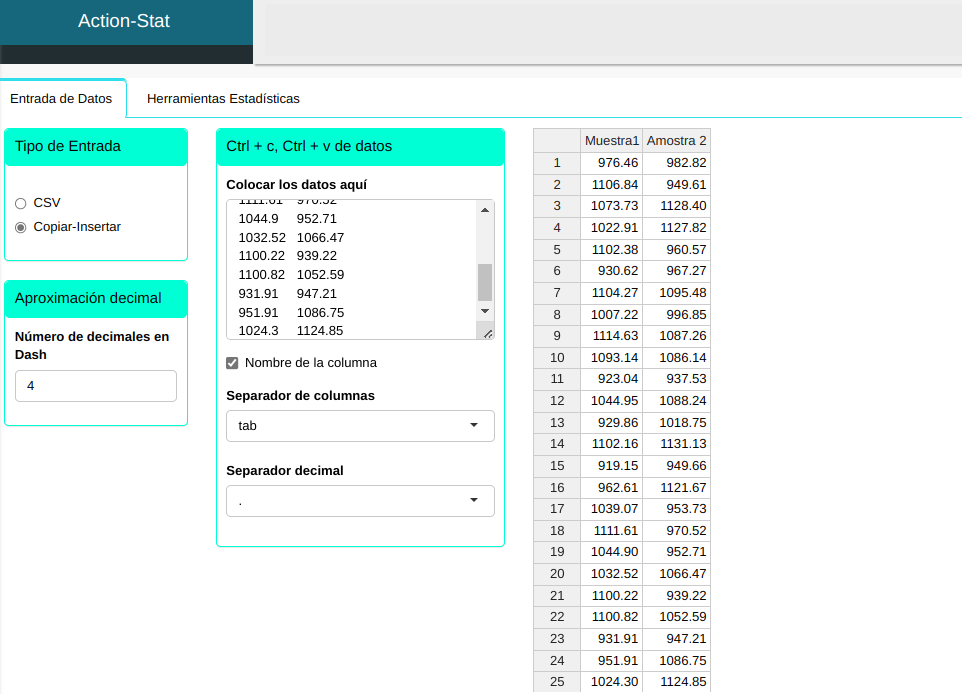
Ajustamos os dados conforme la figura de abajo.
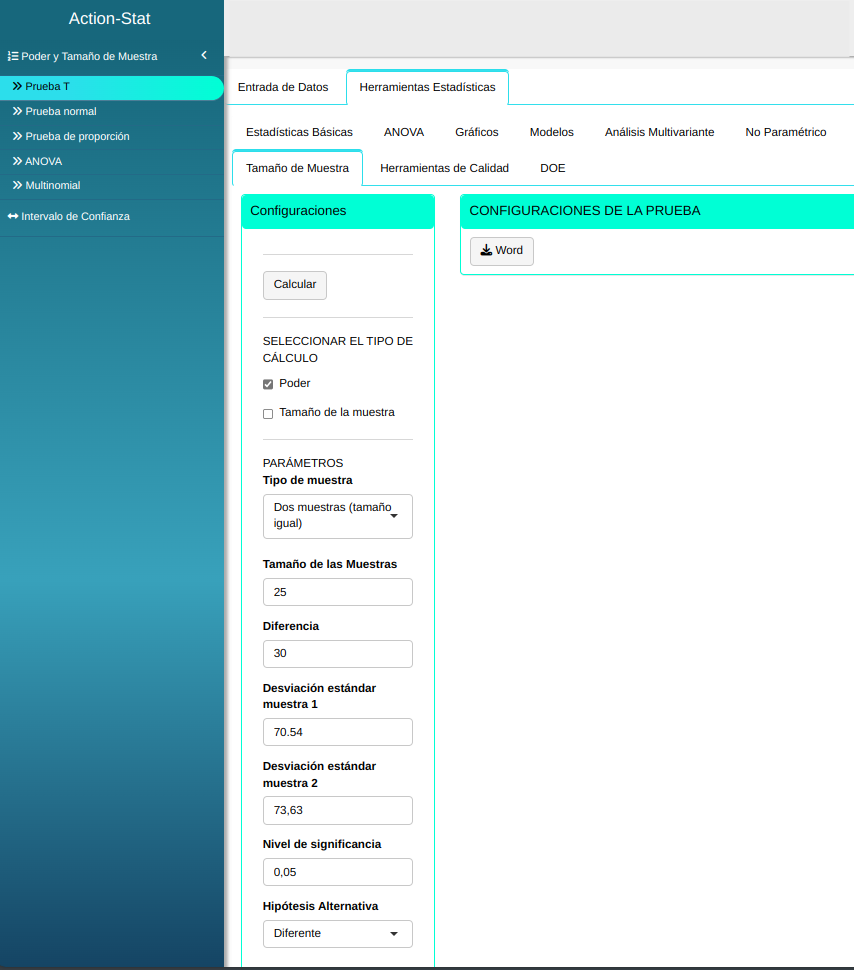
En seguida, haga un clic en calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.
Los resultados son:
Prueba T: dos muestras (tamaños iguales)
| V1 | |
|---|---|
| Poder | 0.302466 |
| Tamaño de la muestra | 25 |
| Diferencia | 30 |
| Desviación Estándar 1 | 70.54 |
| Desviación Estándar 2 | 73.63 |
| Nivel de significancia | 0.05 |
| Hipótesis alternativa | Diferente |
Ejemplo 4:
Supongamos ahora que, con el mismo conjunto de datos, queremos calcular el tamaño de muestra necesario para detectar una diferencia $\mu_1 - \mu_2 = $ 0.6 con un poder de test de al menos 0.9 y una desviación estándar de 1.40434.
| Muestra 1 | Muestra 2 |
|---|---|
| 976.46 | 982.82 |
| 1106.84 | 949.61 |
| 107.73 | 1128.40 |
| 1022.91 | 1127.82 |
| 1102.38 | 960.57 |
| 930.62 | 967.27 |
| 1104.27 | 1095.48 |
| 1007.22 | 996.85 |
| 1114.63 | 1087.26 |
| 1093.14 | 1086.14 |
| 923.04 | 937.53 |
| 1044.95 | 1088.24 |
| 929.86 | 1018.75 |
| 1102.16 | 1131.13 |
| 919.15 | 949.66 |
| 962.61 | 1121.67 |
| 1039.07 | 953.73 |
| 1111.61 | 970.52 |
| 1044.90 | 952.71 |
| 1032.52 | 1066.47 |
| 1100.22 | 939.22 |
| 1100.82 | 1052.59 |
| 931.91 | 947.21 |
| 951.91 | 1086.75 |
| 1024.30 | 1124.85 |
| Poder | $\mathbf{\alpha}$ | Diferença $\mathbf{(\mu_1 - \mu_2)}$ | Desvio-Padrão sp | |
| $\quad$ 0.9 | 0.05 | $\qquad \quad$ 0.6 | $\quad \quad$ 1.40434 |
Ajustamos conforme la figura de abajo.
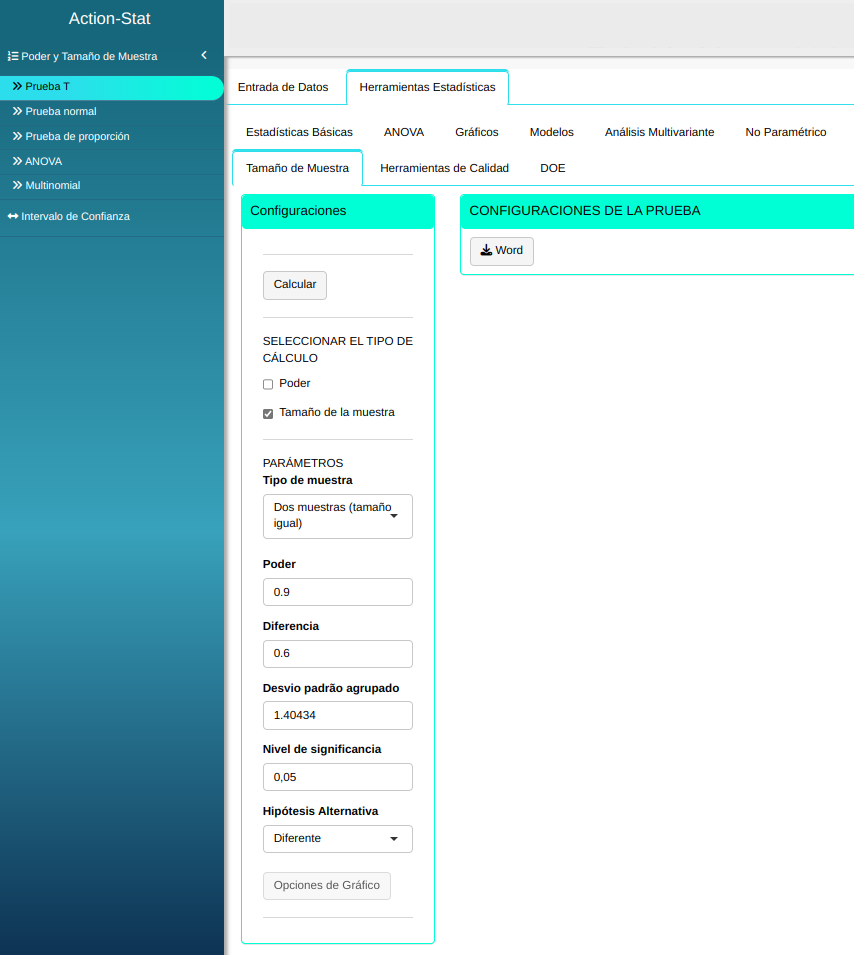
En seguida. haga un clic en calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word
Los resultados son:
Prueba T: dos muestras (tamaños iguales)
| V1 | |
|---|---|
| Poder | 0.9 |
| Tamaño de la muestra | 117 |
| Diferencia | 0.6 |
| Desviación estándar | 1.40434 |
| Nivel de significancia | 0.05 |
| Hipótesis alternativa | Diferente |
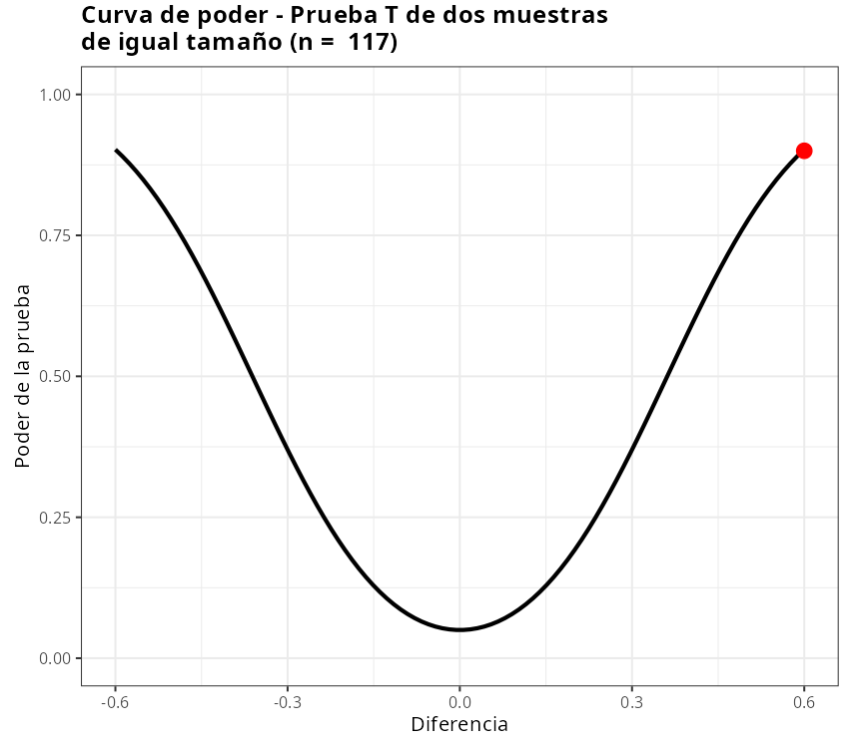
Por lo tanto concluimos que, para detectar una diferencia de 0.6 con una poder de al menos 0.9, es necesario que las dos muestras tengan 117 elementos.
Ejemplo 5:
Compare las medias de las muestras cuyas medidas se presentan en el cuadro siguiente.
| Datos | Muestra |
|---|---|
| 18.8 | Muestra 1 |
| 20.504 | Muestra 1 |
| 18.621 | Muestra 1 |
| 19.919 | Muestra 1 |
| 21.117 | Muestra 1 |
| 17.591 | Muestra 1 |
| 18.756 | Muestra 1 |
| 18.977 | Muestra 1 |
| 20.308 | Muestra 1 |
| 18.899 | Muestra 1 |
| 20.835 | Muestra 1 |
| 17.527 | Muestra 1 |
| 17.078 | Muestra 1 |
| 17.62 | Muestra 1 |
| 21.426 | Muestra 1 |
| 19.169 | Muestra 1 |
| 19.29 | Muestra 1 |
| 22.059 | Muestra 1 |
| 18.585 | Muestra 1 |
| 17.89 | Muestra 1 |
| 18.755 | Muestra 1 |
| 19.203 | Muestra 1 |
| 18.419 | Muestra 1 |
| 20.764 | Muestra 1 |
| 21.055 | Muestra 1 |
| 22.284 | Muestra 2 |
| 21.901 | Muestra 2 |
| 25.302 | Muestra 2 |
| 22.447 | Muestra 2 |
| 22.771 | Muestra 2 |
| 22.057 | Muestra 2 |
| 22.881 | Muestra 2 |
| 17.968 | Muestra 2 |
| 23.382 | Muestra 2 |
| 21.043 | Muestra 2 |
| 22.629 | Muestra 2 |
| 22.86 | Muestra 2 |
| 24.515 | Muestra 2 |
| 22.426 | Muestra 2 |
| 21.203 | Muestra 2 |
| 24.62 | Muestra 2 |
| 22.058 | Muestra 2 |
| 23.15 | Muestra 2 |
| 22.787 | Muestra 2 |
| 24.009 | Muestra 2 |
| 21.491 | Muestra 2 |
| 22.699 | Muestra 2 |
| 24.662 | Muestra 2 |
| 21.983 | Muestra 2 |
| 21.917 | Muestra 2 |
| 21.198 | Muestra 2 |
| 22.909 | Muestra 2 |
| 23.327 | Muestra 2 |
| 24.534 | Muestra 2 |
| 21.152 | Muestra 2 |
Establecer las hipótesis:
- $H_0$: $\mu_1 - \mu_2 = $ 0
- $H_1$: $\mu_1 - \mu_2 \neq $ 0
Primero, necesitamos calcular la desviación estándar. Utilizando la herramienta Resumen descriptivo de Action obteniéndose los valores $s_1$ = 1.36228 y $s_2$ = 1.438224. A continuación, se debe calcular el poder de la prueba T de dos muestras para detectar una diferencia $\mu_1 - \mu_2 =$ 1.5.
| $\mathbf{n_1}$ | $\mathbf{n_2}$ | $\mathbf{\alpha}$ | Diferencia $\mathbf{(\mu_1 - \mu_2)}$ | Desviación Estándar 1 | Desviación Estándar 2 |
| 25 | 30 | 0.05 | $\qquad \quad$ 1.5 | $\qquad$ 1.36228 | $\quad$ 1.43822 |
Subiremos los datos al sistema.
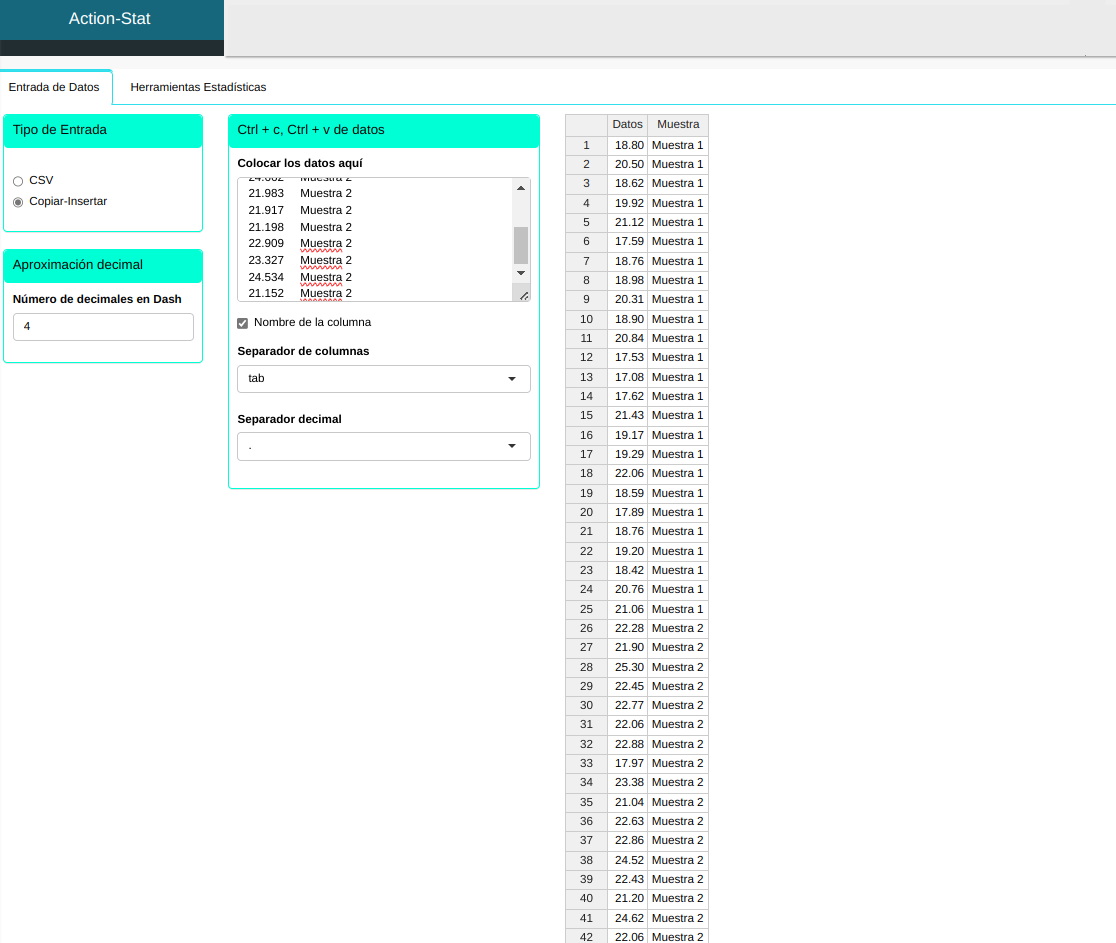
Ajustamos conforme la figura de abajo.
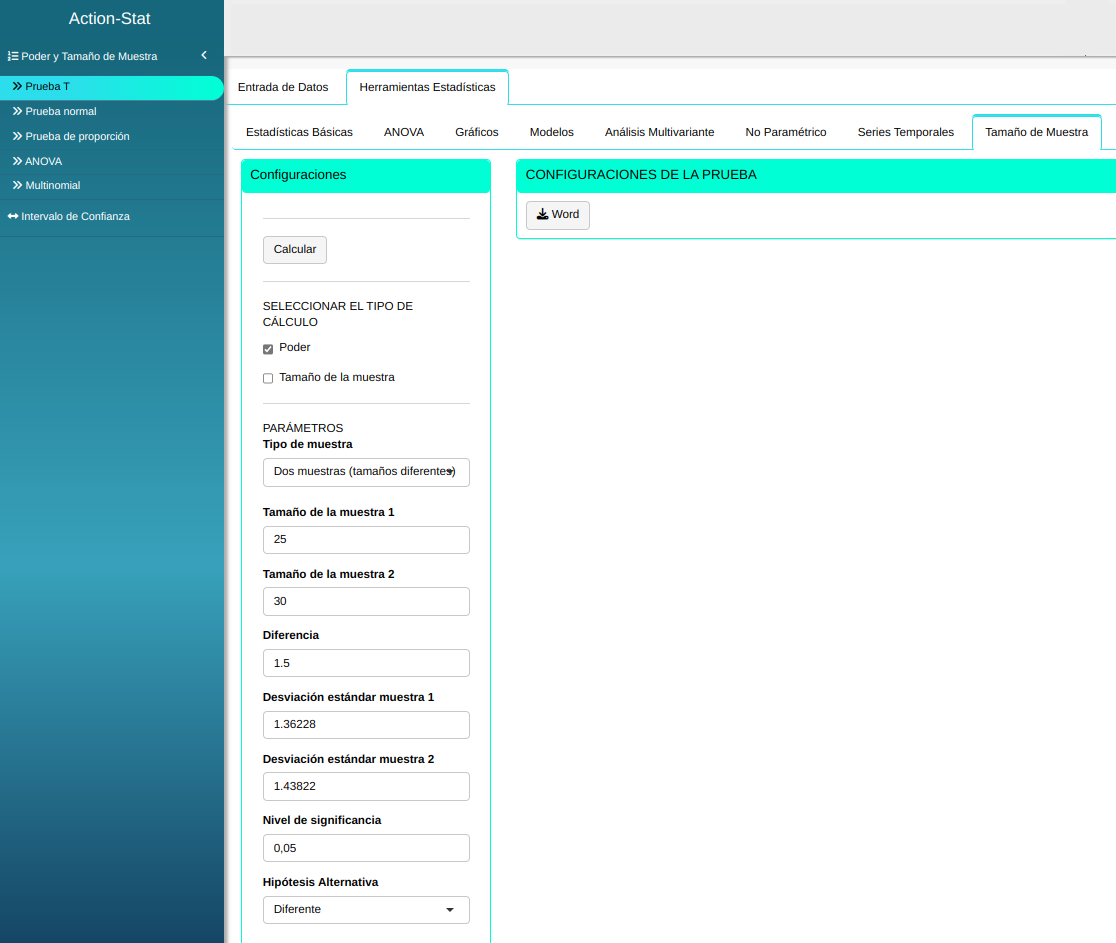
En seguida, haga un clic en calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word
Los resultados son:
Prueba T: dos muestras - tamaños diferentes
| V1 | |
|---|---|
| Poder | 0.9720551 |
| Tamaño de muestra 1 | 25 |
| Tamaño de muestra 2 | 30 |
| Diferencia | 1.5 |
| Desviación Estándar 1 | 1.36228 |
| Desviación Estándar 2 | 1.43822 |
| Nivel de significancia | 0.05 |
| Hipótesis alternativa | Diferente |
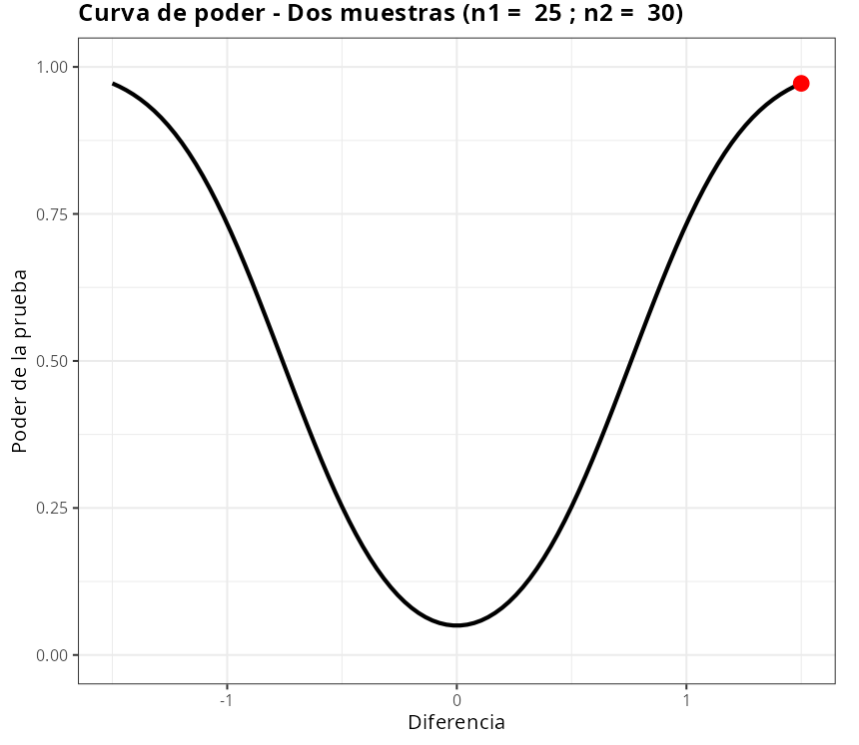
Es decir, para detectar una diferencia d =1.5 entre las medias. esta prueba tiene un poder de 97.20%.
Ejemplo 6:
Usando el ejemplo anterior. supongamos que con un tamaño de muestra de 30. desviación estándar agrupada 1.40434. queremos calcular el tamaño de la otra muestra necesaria para que la prueba T encuentre una diferencia de 1.2. con el poder de al menos el 90%.
| Datos | Muestra |
|---|---|
| 18.8 | Muestra 1 |
| 20.504 | Muestra 1 |
| 18.621 | Muestra 1 |
| 19.919 | Muestra 1 |
| 21.117 | Muestra 1 |
| 17.591 | Muestra 1 |
| 18.756 | Muestra 1 |
| 18.977 | Muestra 1 |
| 20.308 | Muestra 1 |
| 18.899 | Muestra 1 |
| 20.835 | Muestra 1 |
| 17.527 | Muestra 1 |
| 17.078 | Muestra 1 |
| 17.62 | Muestra 1 |
| 21.426 | Muestra 1 |
| 19.169 | Muestra 1 |
| 19.29 | Muestra 1 |
| 22.059 | Muestra 1 |
| 18.585 | Muestra 1 |
| 17.89 | Muestra 1 |
| 18.755 | Muestra 1 |
| 19.203 | Muestra 1 |
| 18.419 | Muestra 1 |
| 20.764 | Muestra 1 |
| 21.055 | Muestra 1 |
| 22.284 | Muestra 2 |
| 21.901 | Muestra 2 |
| 25.302 | Muestra 2 |
| 22.447 | Muestra 2 |
| 22.771 | Muestra 2 |
| 22.057 | Muestra 2 |
| 22.881 | Muestra 2 |
| 17.968 | Muestra 2 |
| 23.382 | Muestra 2 |
| 21.043 | Muestra 2 |
| 22.629 | Muestra 2 |
| 22.86 | Muestra 2 |
| 24.515 | Muestra 2 |
| 22.426 | Muestra 2 |
| 21.203 | Muestra 2 |
| 24.62 | Muestra 2 |
| 22.058 | Muestra 2 |
| 23.15 | Muestra 2 |
| 22.787 | Muestra 2 |
| 24.009 | Muestra 2 |
| 21.491 | Muestra 2 |
| 22.699 | Muestra 2 |
| 24.662 | Muestra 2 |
| 21.983 | Muestra 2 |
| 21.917 | Muestra 2 |
| 21.198 | Muestra 2 |
| 22.909 | Muestra 2 |
| 23.327 | Muestra 2 |
| 24.534 | Muestra 2 |
| 21.152 | Muestra 2 |
| Poder | $\mathbf{\alpha}$ | Diferença $\mathbf{(\mu_1 - \mu_2)}$ | Desvio-Padrão sp | |
| $\quad$ 0.9 | 0.05 | $\qquad \quad$ 1.2 | $\quad \quad$ 1.40434 |
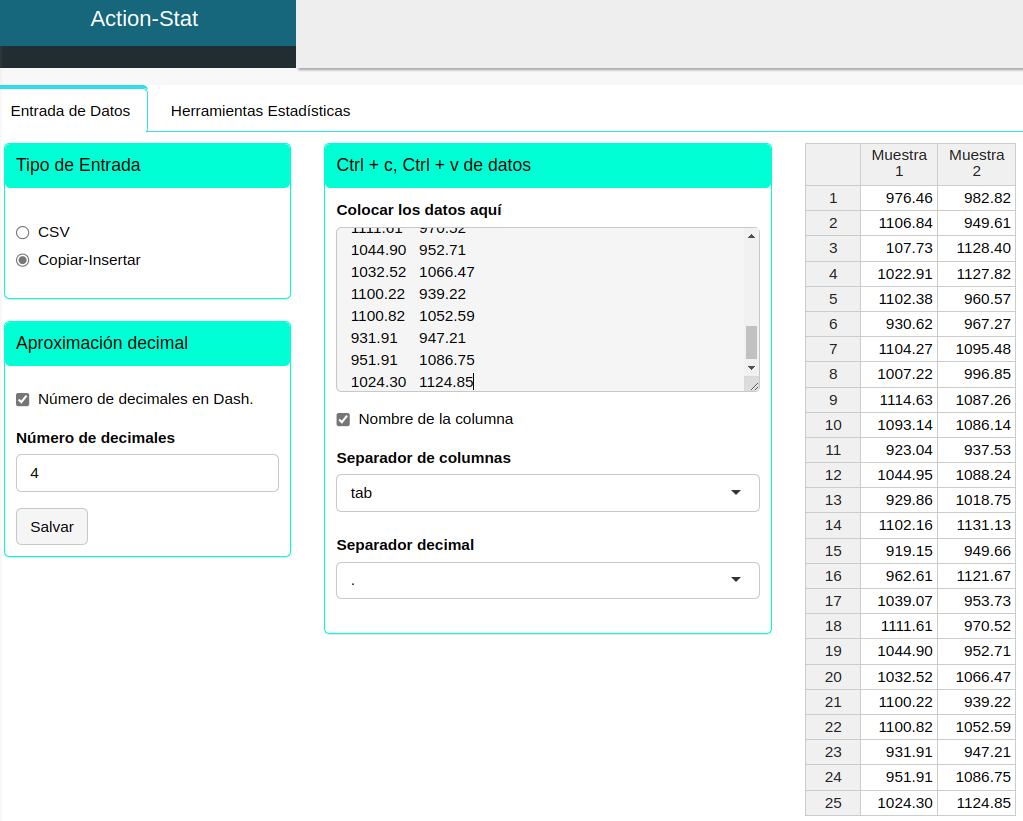Ajustamos conforme la figura de abajo.
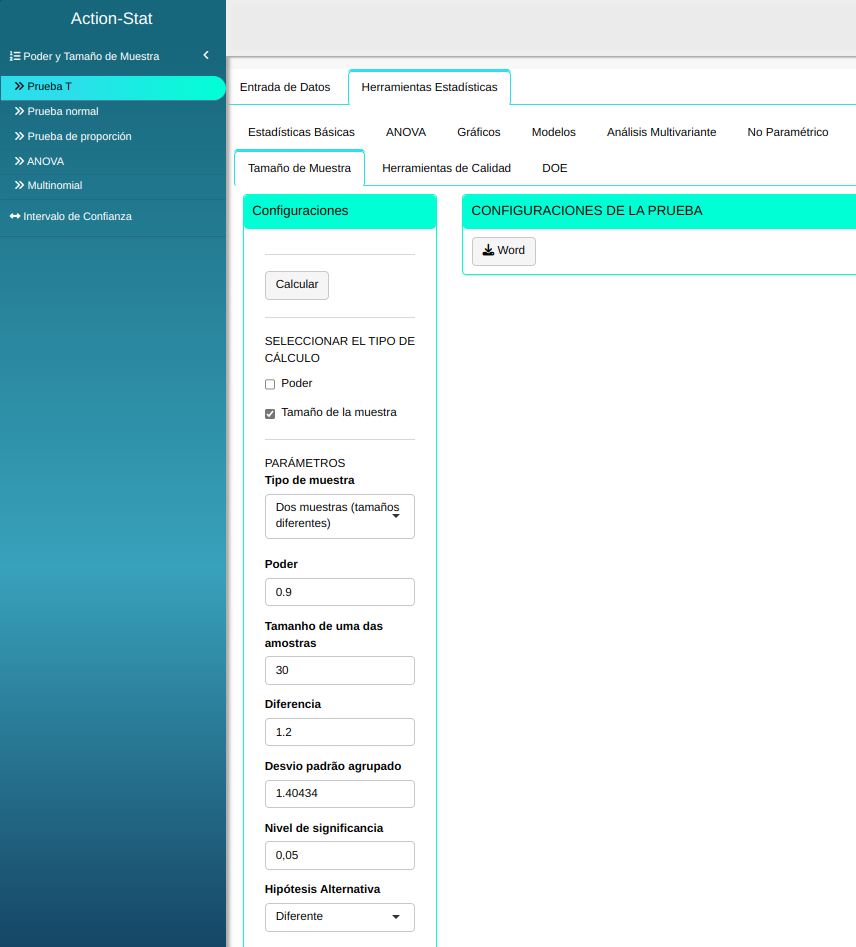
En seguida, haga un clic en calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word
Los resultados son:
Prueba T: dos muestras - tamaños diferentes
| V1 | |
|---|---|
| Poder | 0.9 |
| Tamaño de muestra 1 | 30 |
| Tamaño de muestra 2 | 30 |
| Diferencia | 1.2 |
| Desviación estándar | 1.40434 |
| Nivel de significancia | 0.05 |
| Hipótesis alternativa | Diferente |
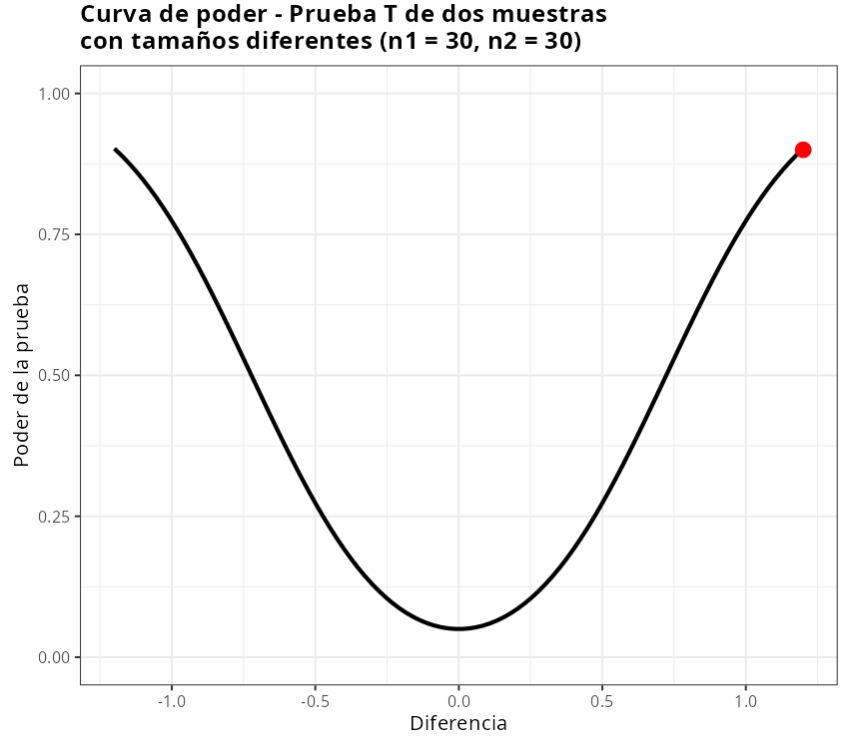
Por tanto, concluimos que. dado que una de las muestras contiene 30 elementos, para detectar una diferencia de 1.2 con un podera de al menos el 90%, es necesario que la otra muestra también tenga aproximadamente 30 elementos.
Ejemplo 7:
Consideremos $X_1, X_2, \ldots , X_{20}$ una muestra de mediciones del laboratorio de la empresa A e $Y_1, Y_2, \ldots , Y_{20}$ una muestra de mediciones del laboratorio de la empresa B. Los ensayos de ambos laboratorios se realizan en el mismo estándar, por lo tanto, existe una correlación entre ellos, es decir, las muestras son dependientes. Evaluar la compatibilidad de mediciones entre el laboratorio de la empresa A y el laboratorio de la empresa B.
| Laboratorio de la empresa A ($X_i$) | Laboratorio de la empresa B ($Y_i$) | Diferencia ($D_i$) |
|---|---|---|
| 1.00552 | 0.01942 | 0.98610 |
| -1.49928 | -0.46512 | -1.03416 |
| 0.21367 | 0.53218 | -0.31851 |
| 0.44658 | -0.14844 | 0.59502 |
| 0.62766 | -0.60021 | 1.22787 |
| 0.31091 | 0.06495 | 0.24596 |
| -0.83878 | 0.33013 | -1.16891 |
| -0.29054 | 0.12116 | -0.41170 |
| -0.08487 | 0.74269 | -0.82756 |
| -1.26465 | -1.64232 | 0.37767 |
| -0.06353 | 0.05497 | -0.11850 |
| -1.07632 | 0.76342 | -1.83974 |
| -1.34134 | 1.74131 | -3.08265 |
| -0.55062 | -0.06392 | -0.48670 |
| 1.61848 | -1.88146 | 3.49994 |
| 0.50997 | -0.76135 | 1.27132 |
| 0.76027 | -0.23009 | 0.99036 |
| 0.68061 | -1.16800 | 1.84861 |
| -1.91464 | 0.88392 | -2.79856 |
| -0.20072 | 0.96512 | -1.16584 |
considerando $D_i = X_i - Y_i$ y estableciendo las hipótesis
- $H_0: \mu_D = $0
- $H_0: \mu_D \neq $0
donde $\mu_D$ se estimará mediante la media muestral de las diferencias, es decir, $D$. Usando la herramienta Estadísticas Básicas de Action, tenemos que la media muestral es $D$ = -0.110499 y la desviación estándar muestral es $S$ = 1.56907778.
Subiremos los datos al sistema.
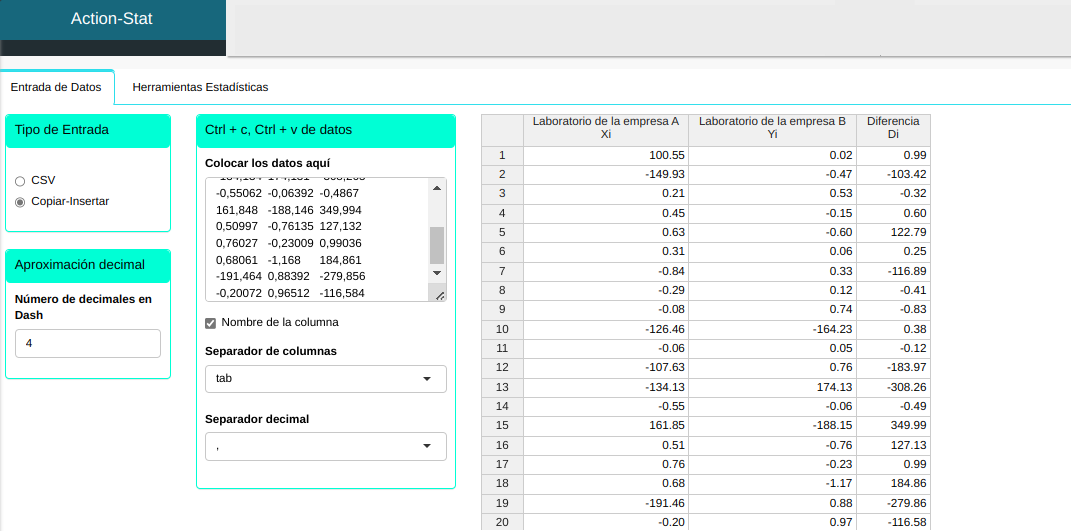
Ajustamos conforme la figura de abajo.
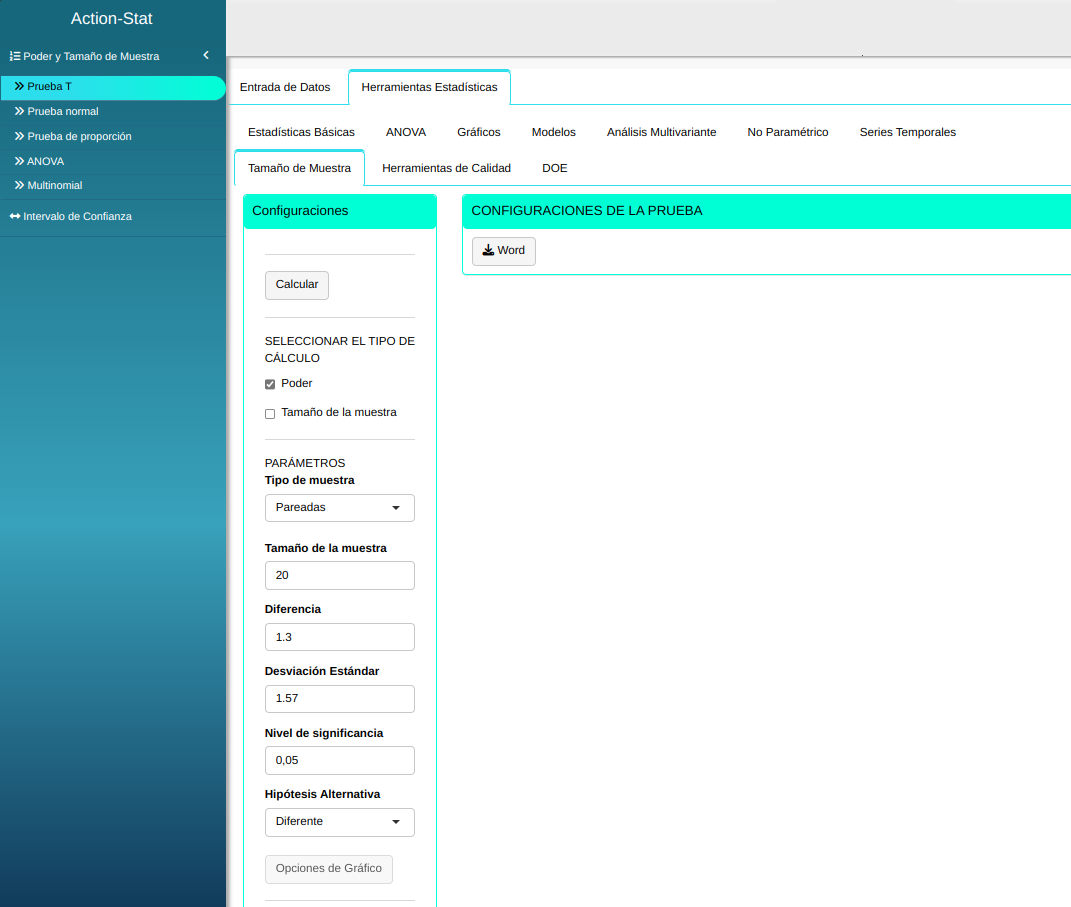
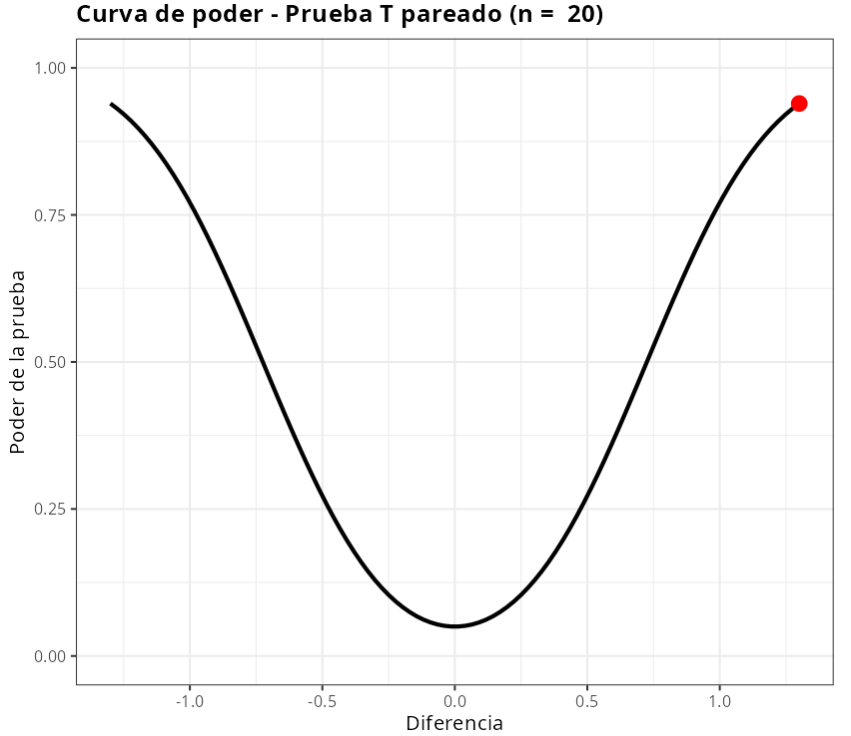
Los resultados son:
Prueba T - Emparejado
| V1 | |
|---|---|
| Poder | 0.9394575 |
| Tamaño de la muestra | 20 |
| Diferencia | 1.3 |
| Nivel de significancia | 0.05 |
| Desviación estándar | 1.57 |
| Hipótesis alternativa | Diferente |
Ejemplo 8:
Usando los datos del ejemplo anterior. Supongamos ahora que queremos calcular el tamaño de muestra necesario para qué la prueba T pareada detecte una diferencia de 0.5 con un poder de al menos el 90%.
Ajustamos conforme la figura de abajo.
Los resultados son:
Prueba T - Pareada
| V1 | |
|---|---|
| Poder | 0.9 |
| Tamaño de la muestra | 106 |
| Diferencia | 0.5 |
| Desviación estándar | 1.57 |
| Nivel de significancia | 0.05 |
| Hipótesis alternativa | Diferente |
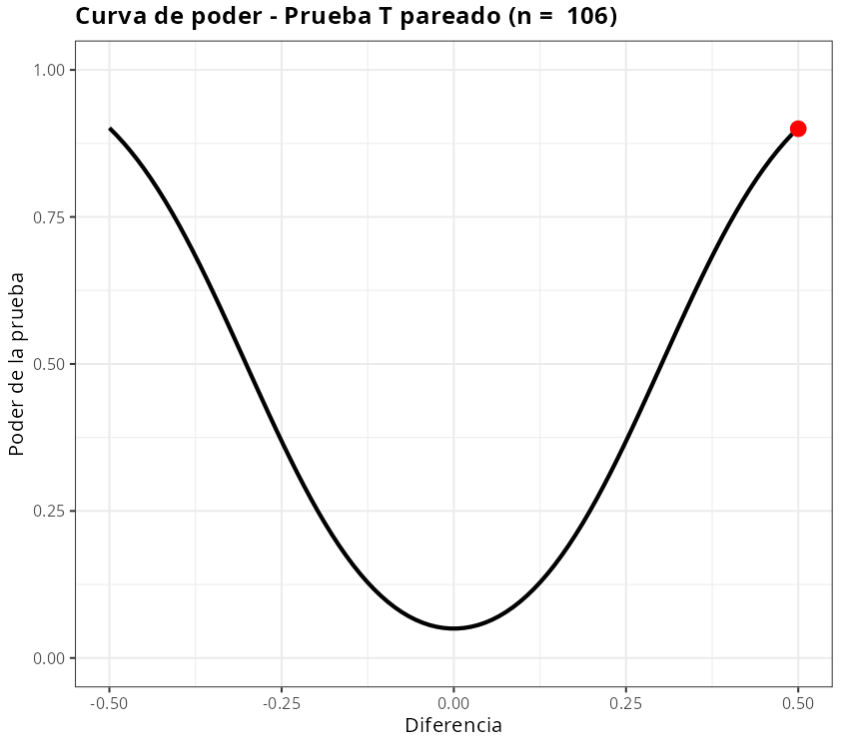
Por lo tanto, para que la prueba detecte una diferencia de 0.5 en la hipótesis con un poder de al menos 0.9, es necesario un tamaño muestra de al menos $n$ = 106.