3. Componentes Principais
A análise de Componentes Principais é um método utilizado para reduzir a dimensão do problema em componentes não correlacionadas que são combinações lineares das variáveis originais. O número dessas componentes é menor ou igual à quantidade de variáveis originais. Esse método é útil quando o número de variáveis em estudo é muito grande.
A ferramenta Componentes Principais do Action permite reduzir a dimensão dos dados através de componentes que são combinações lineares das variáveis originais.
Exemplo 1:
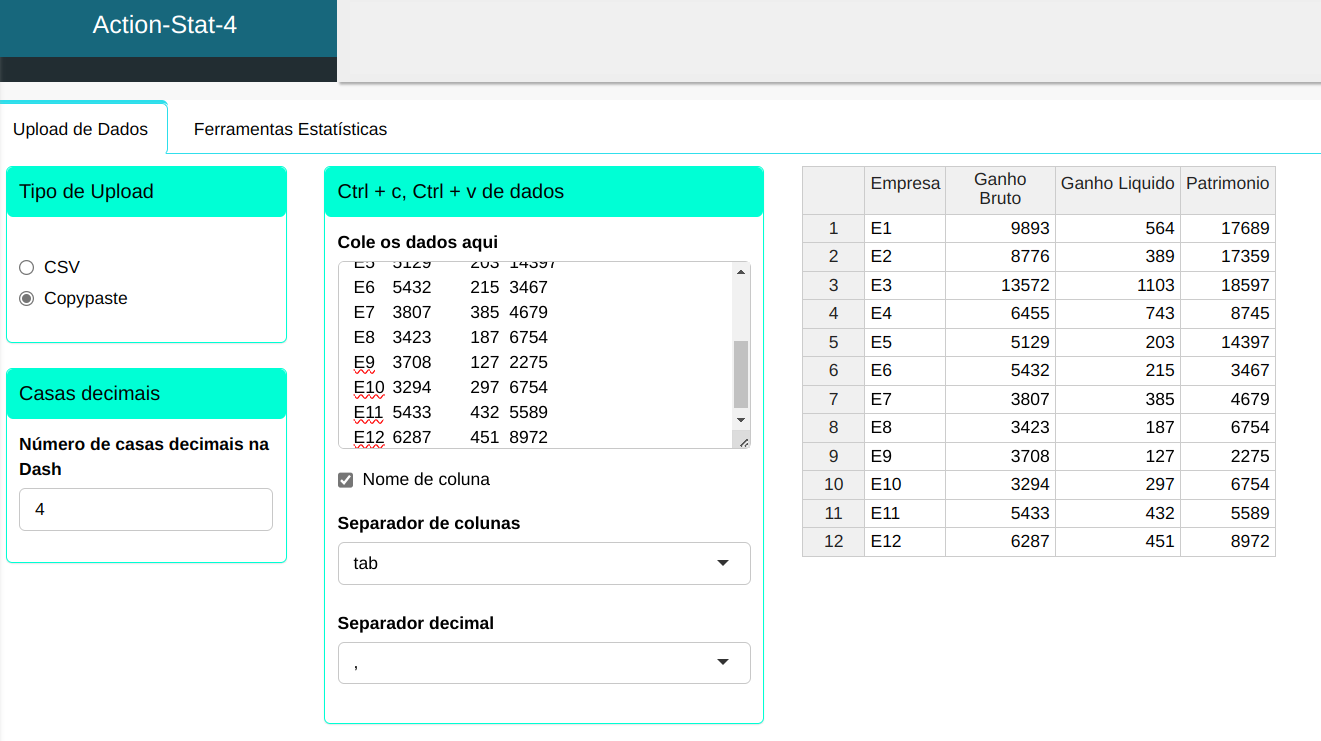
A tabela representa o ganho bruto, ganho líquido e patrimônio, medidas em unidades monetárias, de 12 empresas
| Empresa | Ganho Bruto | Ganho Liquido | Patrimonio |
|---|---|---|---|
| E1 | 9893 | 564 | 17689 |
| E2 | 8776 | 389 | 17359 |
| E3 | 13572 | 1103 | 18597 |
| E4 | 6455 | 743 | 8745 |
| E5 | 5129 | 203 | 14397 |
| E6 | 5432 | 215 | 3467 |
| E7 | 3807 | 385 | 4679 |
| E8 | 3423 | 187 | 6754 |
| E9 | 3708 | 127 | 2275 |
| E10 | 3294 | 297 | 6754 |
| E11 | 5433 | 432 | 5589 |
| E12 | 6287 | 451 | 8972 |
Fazemos a análise de componentes principais e configuramos de acordo com a figura abaixo.

Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
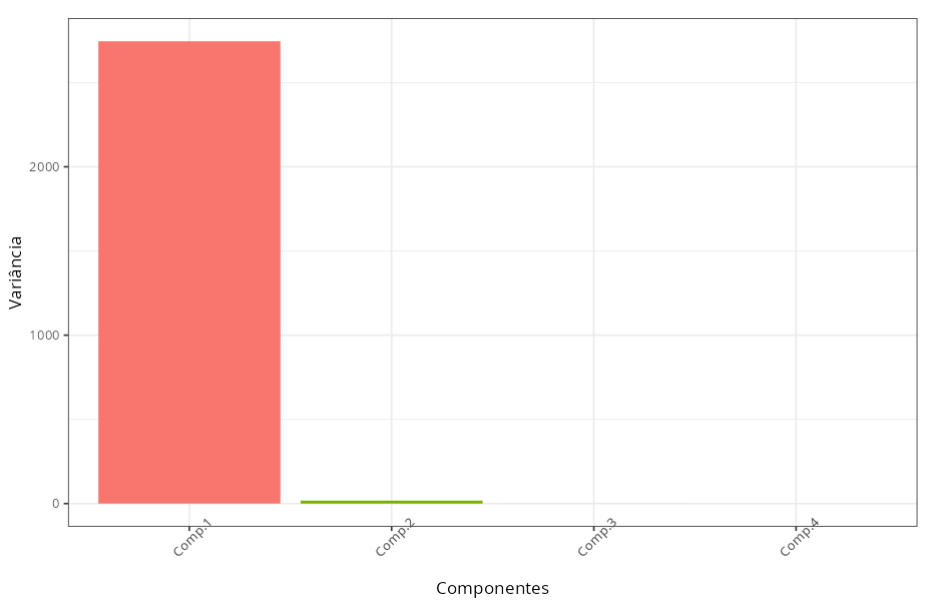
Importância dos componentes
| Informação | Comp.1 | Comp.2 | Comp.3 |
|---|---|---|---|
| Desvio Padrão | 6165.8894 | 1525.7397 | 139.0497 |
| Proporção da variância | 0.9419 | 0.0577 | 0.0005 |
| Proporção Acumulada | 0.9419 | 0.9995 | 1.00 |
Tabela dos centros dos componentes
| Valor do Centro | |
|---|---|
| Ganho bruto | 6267.4167 |
| Ganho Liquido | 424.6667 |
| Patrimônio | 9606.4167 |
Matriz de Correlação
| Comp.1 | Comp.2 | Comp.3 | |
|---|---|---|---|
| Comp.1 | 1 | 0 | 0 |
| Comp.2 | 0 | 1 | 0 |
| Comp.3 | 0 | 0 | 1 |
Resultado da análise
| Comp.1 | Comp.2 | Comp.3 | |
|---|---|---|---|
| Ganho Bruto | 0.425 | 0.900 | 0.099 |
| Ganho Liquido | 0.028 | 0.097 | -0.995 |
| Patrimônio | 0.905 | -0.426 | -0.016 |
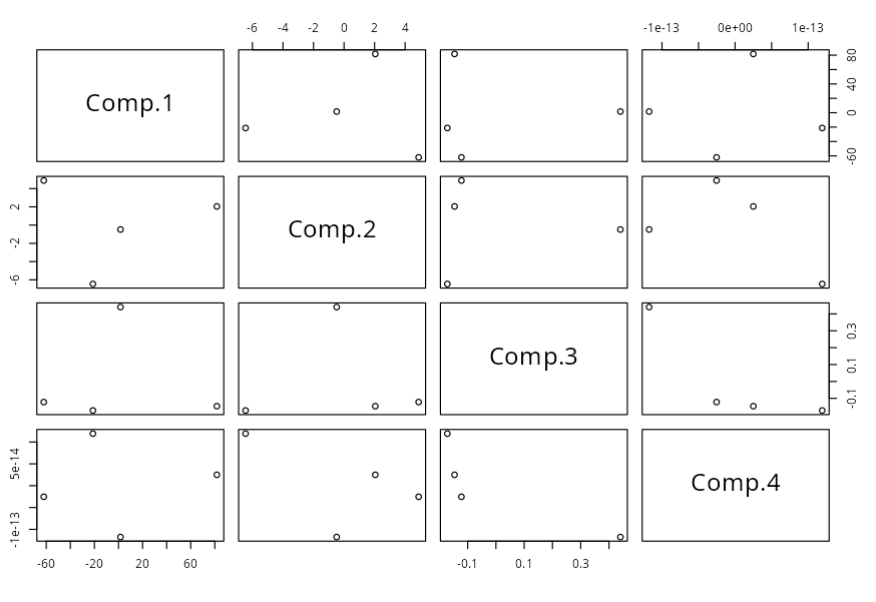
Resultado da análise
| Comp.1 | Comp.2 | Comp.3 | |
|---|---|---|---|
| E1 | 8857.594 | -165.267 | 90.180 |
| E2 | 8079.361 | -1046.652 | 158.932 |
| E3 | 11257.926 | 2810.250 | -96.180 |
| E4 | -690.799 | 566.191 | -284.231 |
| E5 | 3844.091 | -3084.941 | 30.403 |
| E6 | -5915.416 | 1841.624 | 224.925 |
| E7 | -5504.970 | -119.929 | -124.811 |
| E8 | -3796.380 | -1367.834 | 0.640 |
| E9 | -7729.150 | 789.459 | 160.881 |
| E10 | -3848.175 | -1473.279 | -121.587 |
| E11 | -3989.162 | 960.153 | -25.133 |
| E12 | -564.919 | 290.226 | -14.019 |
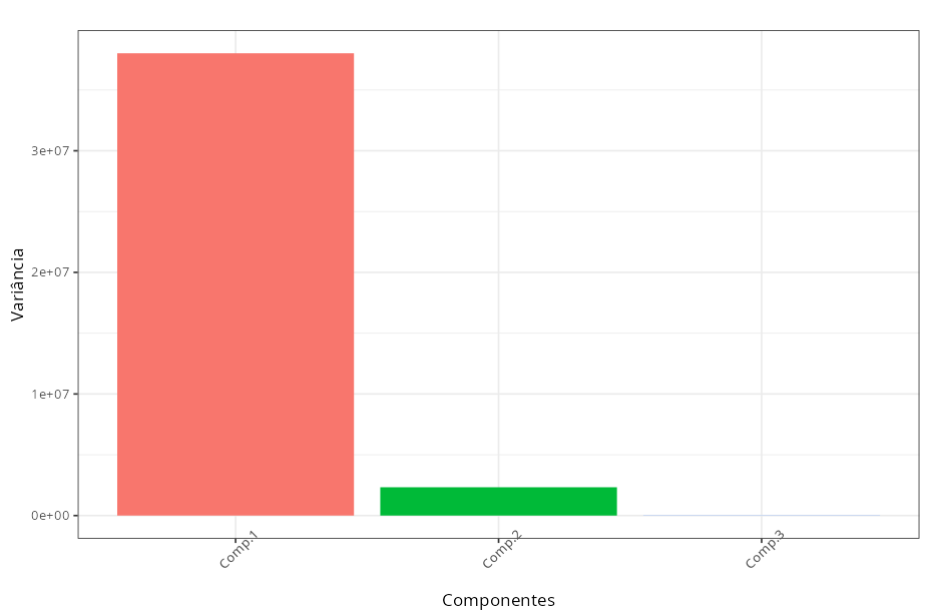
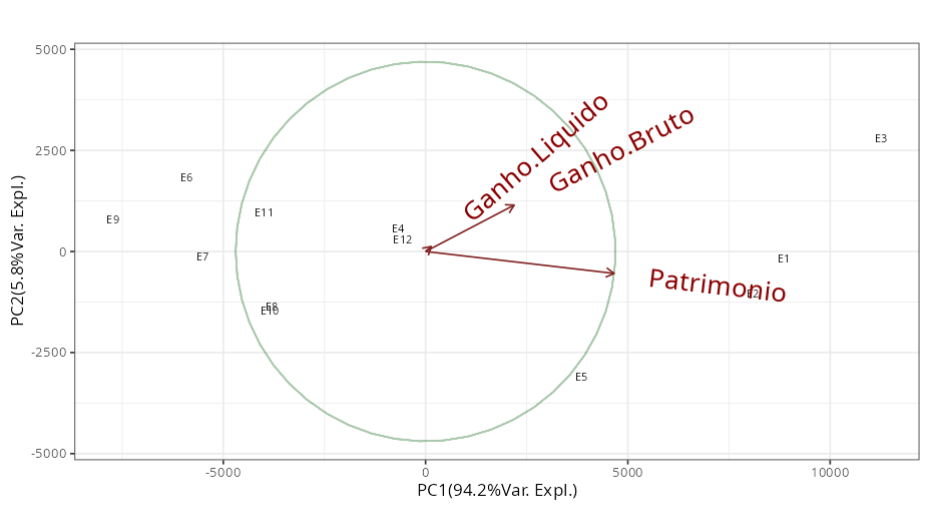
A primeira componente principal explica 94,18% da variação total. As variável ganho bruto e patrimônio têm pesos negativamente altos na primeira componente principal, -0,425 e -0.905 respectivamente; a variável ganho líquido praticamente não afeta essa componente, pois o seu peso é muito baixo, -0,02.
Assim, a primeira componente pode ser interpretada como um índice de desempenho global das empresas. Como os pesos são negativos, quando maior for o ganho bruto e o patrimônio da empresa, menor é o valor dessa componente e melhor é o índice global de desempenho da empresa. As empresas E3, E1 e E2 tiveram os melhores índices de desempenho, respectivamente, enquanto a empresa que ficou com o pior índice foi a E9.
Exemplo 2:
Cinco juízes avaliaram 8 marcas de coxinha de galinha em relação ao sabor, aroma, qualidade da massa e qualidade do recheio. Cada juiz deu uma nota de 1 a 5 representando a qualidade das coxinhas. A tabela contém as notas dos juízes referentes à qualidade de cada marca coxinha.
| Marca | Sabor | Aroma | Massa | Recheio |
|---|---|---|---|---|
| M1 | 2,75 | 4,03 | 2,8 | 2,62 |
| M2 | 3,9 | 4,12 | 3,4 | 3,52 |
| M3 | 3,12 | 3,97 | 3,62 | 3,05 |
| M4 | 4,58 | 4,86 | 4,34 | 4,82 |
| M5 | 3,97 | 4,34 | 4,28 | 4,98 |
| M6 | 3,01 | 3,98 | 2,9 | 2,82 |
| M7 | 4,19 | 4,65 | 4,52 | 4,77 |
| M8 | 3,82 | 4,12 | 3,62 | 3,71 |
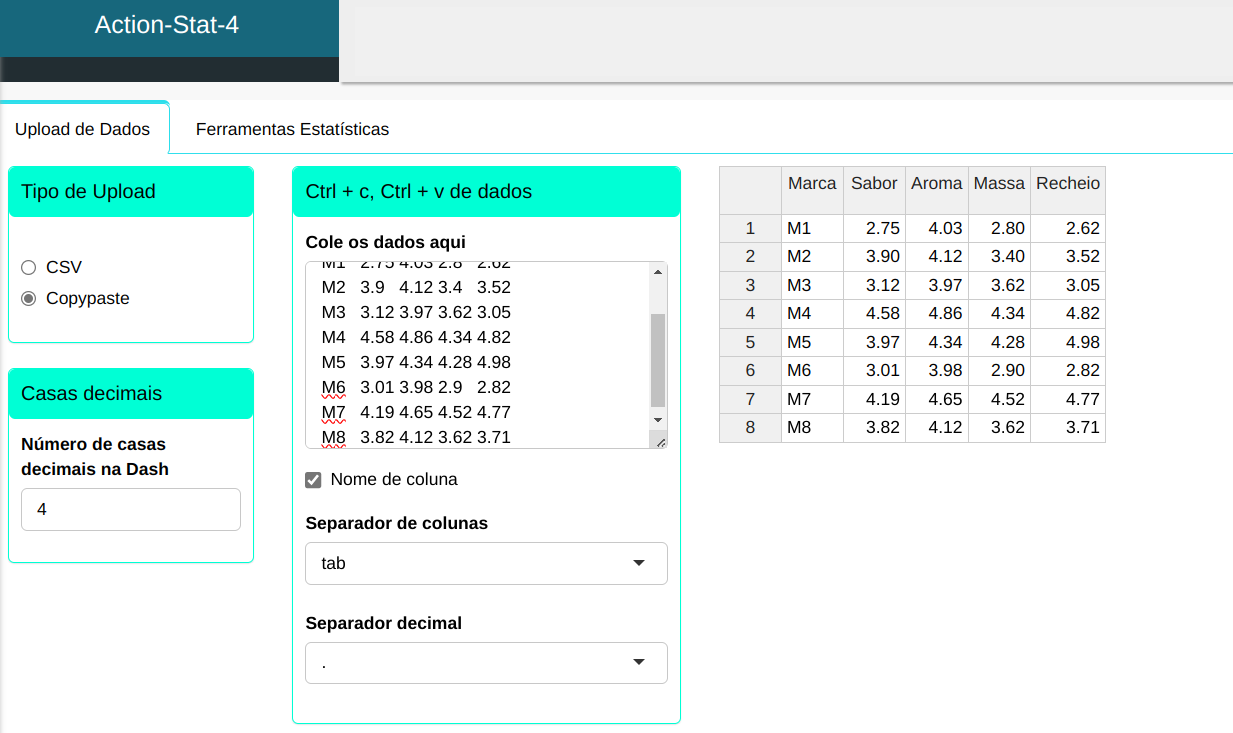
Faremos a análise de componentes principais e configuramos de acordo com a figura abaixo.

Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Importância dos componentes
| Informação | Comp.1 | Comp.2 | Comp.3 | Comp.4 |
|---|---|---|---|---|
| Desvio Padrão | 1.905 | 0.442 | 0.361 | 0.210 |
| Proporção da variância | 0.908 | 0.049 | 0.033 | 0.011 |
| Proporção Acumulada | 0.908 | 0.956 | 0.989 | 1.000 |
Tabela dos centros dos componentes
| Valor do Centro | |
|---|---|
| Sabor | 3.668 |
| Aroma | 4.259 |
| Massa | 3.685 |
| Recheio | 3.786 |
Matriz de Correlação
| Comp.1 | Comp.2 | Comp.3 | Comp.4 | |
|---|---|---|---|---|
| Comp.1 | 1 | 0 | 0 | 0 |
| Comp.2 | 0 | 1 | 0 | 0 |
| Comp.3 | 0 | 0 | 1 | 0 |
| Comp.4 | 0 | 0 | 0 | 1 |
Resultado da análise
| Comp.1 | Comp.2 | Comp.3 | Comp.4 | |
|---|---|---|---|---|
| Sabor | 0.499 | 0.153 | 0.825 | 0.216 |
| Aroma | 0.488 | 0.756 | -0.436 | 0.003 |
| Massa | 0.502 | -0.532 | -0.357 | 0.582 |
| Recheio | 0.511 | -0.349 | -0.039 | -0.784 |
Resultado da análise
| Comp.1 | Comp.2 | Comp.3 | Comp.4 | |
|---|---|---|---|---|
| M1 | -2.523 | 0.437 | -0.378 | -0.154 |
| M2 | -0.410 | 0.075 | 0.695 | 0.045 |
| M3 | -1.386 | -0.498 | -0.281 | 0.384 |
| M4 | 2.838 | 0.721 | -0.011 | 0.053 |
| M5 | 1.554 | -0.711 | -0.097 | -0.371 |
| M6 | -2.187 | 0.216 | -0.016 | -0.141 |
| M7 | 2.302 | -0.028 | -0.359 | 0.126 |
| M8 | -0.187 | -0.212 | 0.447 | 0.059 |
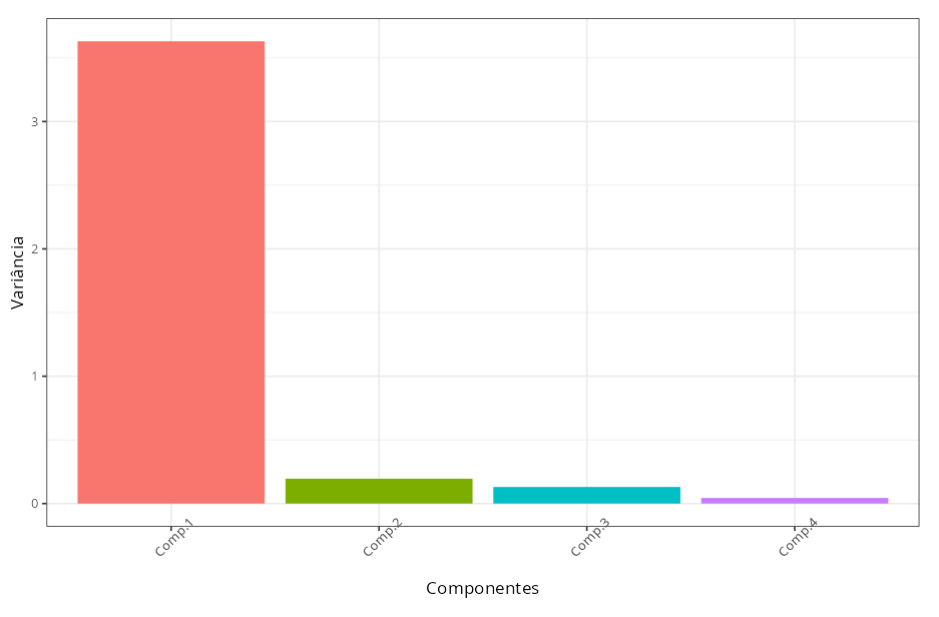
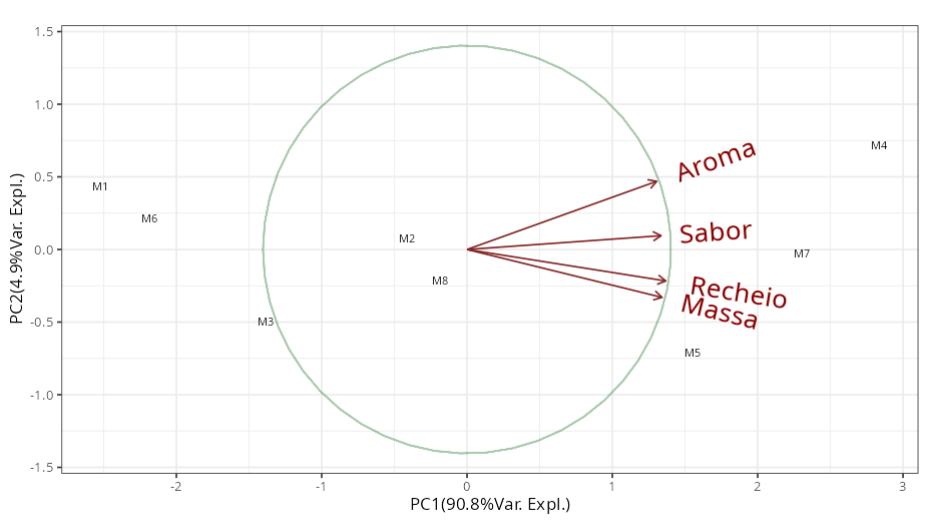
A primeira componente principal explica 90,8% da variação total e de acordo com a tabela dos autovetores os pesos das variáveis massa, recheio, sabor e aroma são negativamente altos para essa componente, ou seja, quanto maior a nota dessas variáveis, menor é o escore da primeira componente. Então, a primeira componente principal pode ser entendida como um índice global da qualidade da coxinha de acordo com os juízes.
Assim, escore mais baixo na primeira componente indica que o índice de qualidade é melhor, ou seja, quanto menor o escore dessa componente, melhor é a coxinha. De acordo com a tabela de escores obtida nessa análise, as marcas M4, M5 e M7 possuem as melhores coxinhas enquanto que a pior coxinha é da marca M1.
Exemplo 3:
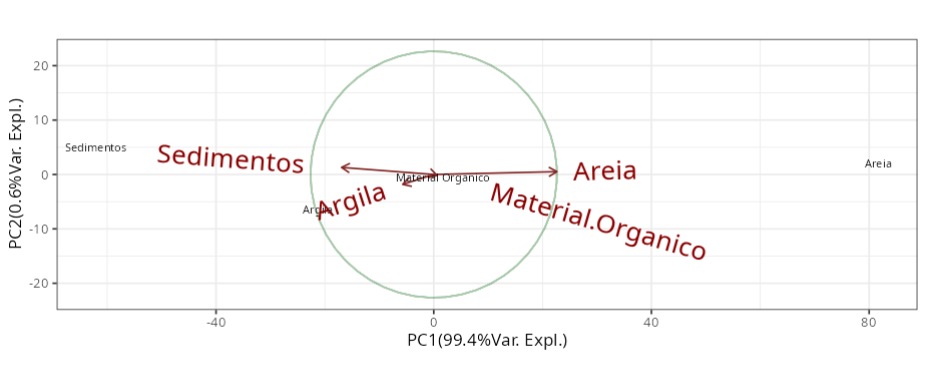
Um estudo coletou 25 amostras de um determinado solo. Para cada amostra mediu-se a porcentagem de areia (X1), sedimentos (X2), argila (X3) e a quantidade de material orgânico (X4). A matriz de covariância dos dados analisados está na tabela.
| Areia | Sedimentos | Argila | Material Orgânico | |
|---|---|---|---|---|
| Areia | 64,96 | -47,22 | -17,74 | 1,58 |
| Sedimentos | -47,22 | 38,8 | 8,42 | -1,62 |
| Argila | -17,74 | 8,42 | 9,31 | 0,04 |
| Material Orgânico | 1,58 | -1,62 | 0,04 | 0,68 |
Faremos a análise de componentes principais e configuramos de acordo com a figura abaixo.

Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Importância dos componentes
| Informação | Comp.1 | Comp.2 | Comp.3 | Comp.4 |
|---|---|---|---|---|
| Desvio Padrão | 52.397 | 4.180 | 0.255 | 0 |
| Proporção da variância | 0.994 | 0.006 | 0.000 | 0 |
| Proporção Acumulada | 0.994 | 1.000 | 1.000 | 1 |
Tabela dos centros dos componentes
| Valor do Centro | |
|---|---|
| Areia | 0.395 |
| Sedimentos | -0.405 |
| Argila | 0.008 |
| Material orgânico | 0.170 |
Matriz de Correlação
| Comp.1 | Comp.2 | Comp.3 | Comp.4 | |
|---|---|---|---|---|
| Comp.1 | 1 | 0 | 0 | 0.050 |
| Comp.2 | 0 | 1 | 0 | -0.548 |
| Comp.3 | 0 | 0 | 1 | -0.835 |
| Comp.4 | 0.05 | -0.548 | -0.835 | 1.000 |
Resultado da análise
| Comp.1 | Comp.2 | Comp.3 | Comp.4 | |
|---|---|---|---|---|
| Areia | 0.785 | 0.226 | 0.003 | 0.577 |
| Sedimentos | -0.587 | 0.565 | 0.057 | 0.577 |
| Argila | -0.198 | -0.790 | -0.053 | 0.578 |
| Material.orgânico | 0.021 | -0.075 | 0.997 | -0.004 |
Resultado da análise
| Comp.1 | Comp.2 | Comp.3 | Comp.4 | |
|---|---|---|---|---|
| Areia | 81.689 | 2.045 | -0.146 | 0 |
| Sedimentos | -62.083 | 4.886 | -0.122 | 0 |
| Argila | -21.253 | -6.449 | -0.172 | 0 |
| Material orgânico | 1.648 | -0.483 | 0.440 | 0 |