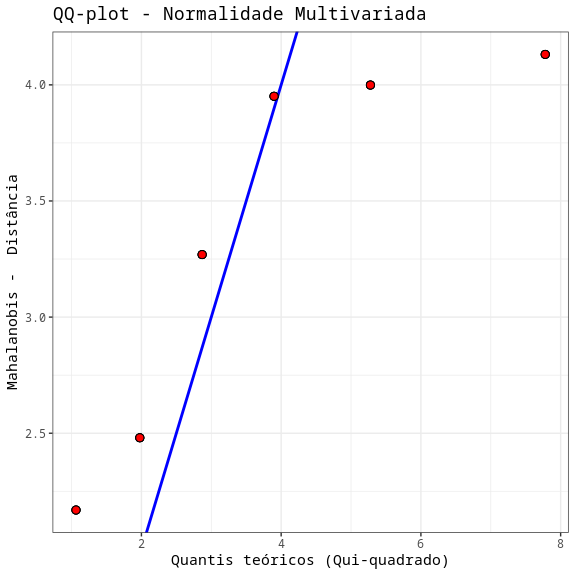
6. MANOVA
A análise de variância multivariada (MANOVA) é uma forma generalizada da análise de variância (ANOVA). É utilizada em casos onde existem duas ou mais variáveis dependentes.
Exemplo 1:
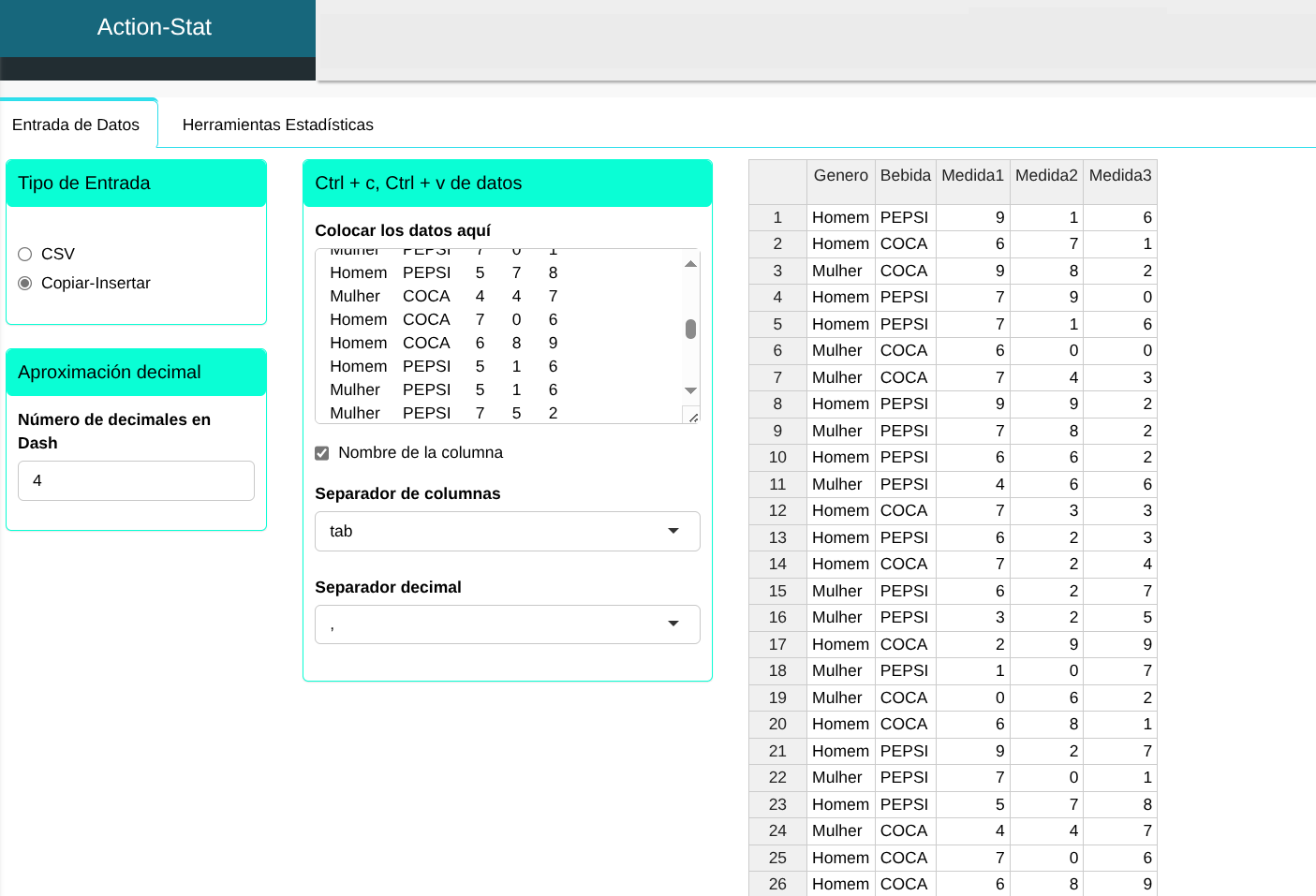
Cada linha da tabela abaixo representa um gerente de compra de grandes redes de restaurantes, A coluna gênero identifica o gênero do gerente, bebida identifica a bebida que serve "Coca" ou "Pepsi" e as variáveis Medida1, Medida2 e Medida3 contém informações relacionadas às compras dos últimos 23 meses da companhia.
O objetivo da análise é identificar se algum gerente comprou mais que outro e se alguma bebida foi mais comprada que a outra. Vamos utilizar a MANOVA para analisar o modelo de 1º Ordem e com Interação 2-way das variáveis Gênero e Bebida.
| Gênero | Bebida | Medida1 | Medida2 | Medida3 |
|---|---|---|---|---|
| Homem | PEPSI | 9 | 1 | 6 |
| Homem | COCA | 6 | 7 | 1 |
| Mulher | COCA | 9 | 8 | 2 |
| Homem | PEPSI | 7 | 9 | 0 |
| Homem | PEPSI | 7 | 1 | 6 |
| Mulher | COCA | 6 | 0 | 0 |
| Mulher | COCA | 7 | 4 | 3 |
| Homem | PEPSI | 9 | 9 | 2 |
| Mulher | PEPSI | 7 | 8 | 2 |
| Homem | PEPSI | 6 | 6 | 2 |
| Mulher | PEPSI | 4 | 6 | 6 |
| Homem | COCA | 7 | 3 | 3 |
| Homem | PEPSI | 6 | 2 | 3 |
| Homem | COCA | 7 | 2 | 4 |
| Mulher | PEPSI | 6 | 2 | 7 |
| Mulher | PEPSI | 3 | 2 | 5 |
| Homem | COCA | 2 | 9 | 9 |
| Mulher | PEPSI | 1 | 0 | 7 |
| Mulher | COCA | 0 | 6 | 2 |
| Homem | COCA | 6 | 8 | 1 |
| Homem | PEPSI | 9 | 2 | 7 |
| Mulher | PEPSI | 7 | 0 | 1 |
| Homem | PEPSI | 5 | 7 | 8 |
| Mulher | COCA | 4 | 4 | 7 |
| Homem | COCA | 7 | 0 | 6 |
| Homem | COCA | 6 | 8 | 9 |
| Homem | PEPSI | 5 | 1 | 6 |
| Mulher | PEPSI | 5 | 1 | 6 |
| Mulher | PEPSI | 7 | 5 | 2 |
| Homem | COCA | 3 | 6 | 0 |
| Homem | PEPSI | 2 | 3 | 9 |
| Mulher | COCA | 1 | 7 | 2 |
| Mulher | PEPSI | 9 | 7 | 8 |
| Homem | COCA | 9 | 2 | 2 |
| Homem | COCA | 7 | 9 | 8 |
| Homem | COCA | 5 | 3 | 5 |
| Mulher | PEPSI | 7 | 6 | 5 |
| Mulher | PEPSI | 6 | 7 | 3 |
| Mulher | PEPSI | 5 | 1 | 3 |
| Homem | COCA | 7 | 6 | 2 |
| Homem | PEPSI | 3 | 5 | 2 |
| Homem | COCA | 5 | 5 | 7 |
| Mulher | PEPSI | 2 | 5 | 1 |
| Homem | PEPSI | 9 | 4 | 0 |
| Homem | COCA | 9 | 2 | 6 |
| Homem | PEPSI | 8 | 8 | 3 |
| Mulher | COCA | 9 | 4 | 2 |
| Mulher | PEPSI | 7 | 5 | 4 |
| Mulher | COCA | 7 | 9 | 8 |
| Homem | COCA | 5 | 2 | 4 |
Fazemos a análise e configuramos conforme a figura abaixo.
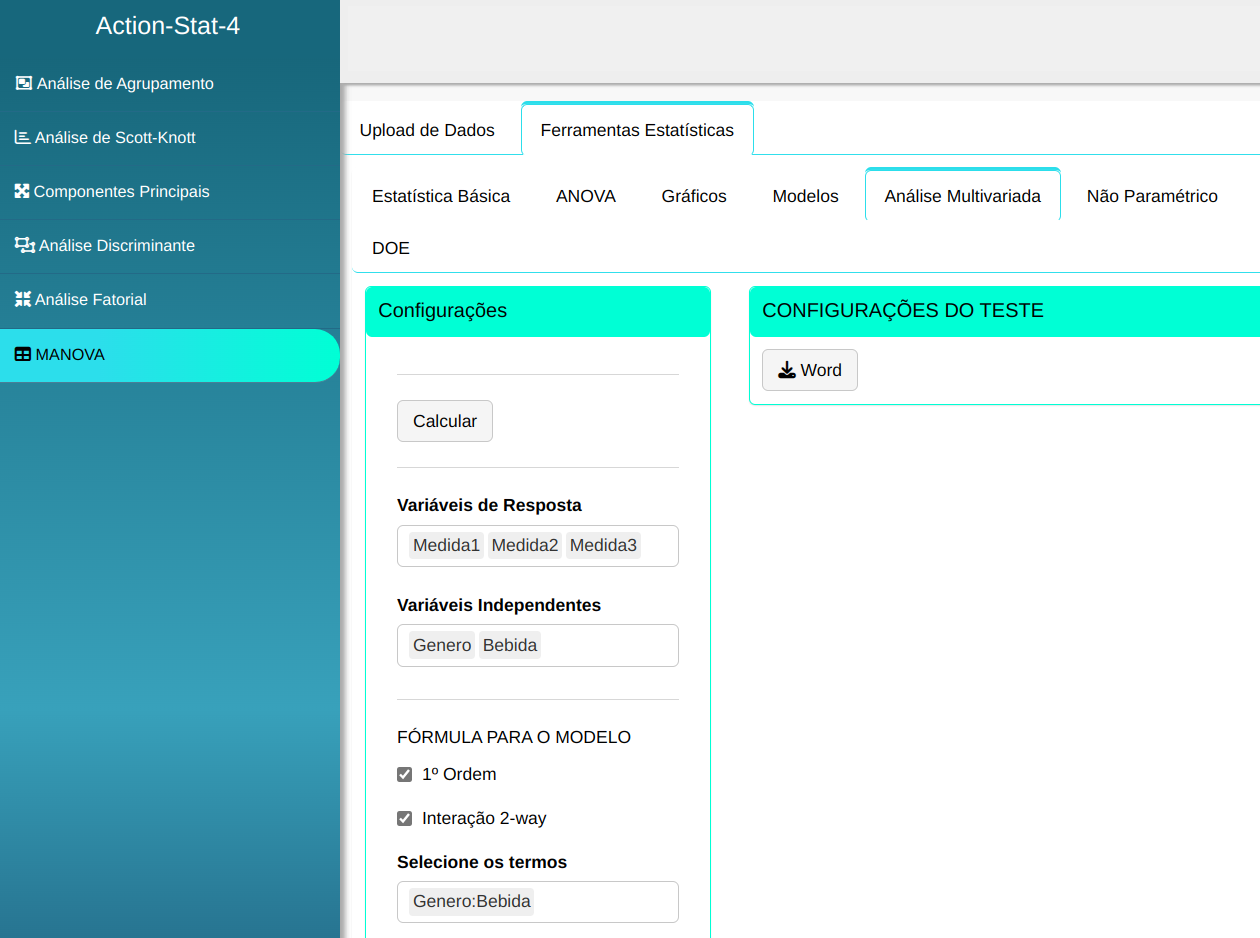

Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Tabela das médias por grupo
| Grupos | Bebida | Medida1 | Medida2 | Medida3 |
|---|---|---|---|---|
| Homem | COCA | 6.067 | 4.800 | 4.467 |
| Mulher | COCA | 5.375 | 5.250 | 3.250 |
| Homem | PEPSI | 6.538 | 4.462 | 4.154 |
| Mulher | PEPSI | 5.429 | 3.929 | 4.286 |
Matriz de Covariâncias
| Medida1 | Medida2 | Medida3 | |
|---|---|---|---|
| Medida1 | 5.602 | 0.096 | -0.680 |
| Medida2 | 0.096 | 8.335 | -0.465 |
| Medida3 | -0.680 | -0.465 | 7.429 |
Tabela da MANOVA
| G.L. | Estat.Wilks | Estat.F | G.L.Numerador | G.L.Denominador | P-valor | |
|---|---|---|---|---|---|---|
| Gênero | 1 | 0.954 | 0.703 | 3 | 44 | 0.555 |
| Bebida | 1 | 0.977 | 0.349 | 3 | 44 | 0.790 |
| Gênero:Bebida | 1 | 0.978 | 0.324 | 3 | 44 | 0.808 |
| Resíduos | 46 |
Pelos testes de Wilks da tabela de MANOVA podemos concluir que não há diferença significativa relacionadas às compras dos últimos 23 meses pelo fator bebida e nem pelo fator gênero, A interação também não é significativa.
Exemplo 2:
Dois grupos/tipo de tratamento (A e B) foram efetuadas em uma amostra com quatro medições em intervalos de tempo igualmente espaçados. O Tratamento A corresponde ao ativo e 0 B, ao Placebo.
Questões de interesse
-
Globalmente, existem diferenças significativas entre os pontos TEMPO?
-
Será que os dois grupos diferem em algum momento, ou seja, há um efeito do tratamento?
-
Será que os dois grupos diferem em suas respostas ao longo do tempo, ou seja, há uma interação TEMPO * TRATAMENTO?
Premissas
-
Ambas as medidas repetidas ANOVA e MANOVA supõe que os intervalos de tempo são igualmente espaçados.
-
Ambos os métodos de assumir a resposta é normalmente distribuída, mas ambas as abordagens são robustas contra as violações da normalidade.
-
Ambas as abordagens exigem dados completos sobre todos os assuntos, isto é, sem observações em falta para quaisquer assuntos.
| Grupo | Tempo1 | Tempo2 | Tempo3 | Tempo4 |
|---|---|---|---|---|
| A | 31 | 29 | 15 | 26 |
| A | 24 | 28 | 20 | 32 |
| A | 14 | 20 | 28 | 30 |
| B | 38 | 34 | 30 | 34 |
| B | 25 | 29 | 25 | 29 |
| B | 30 | 28 | 16 | 34 |
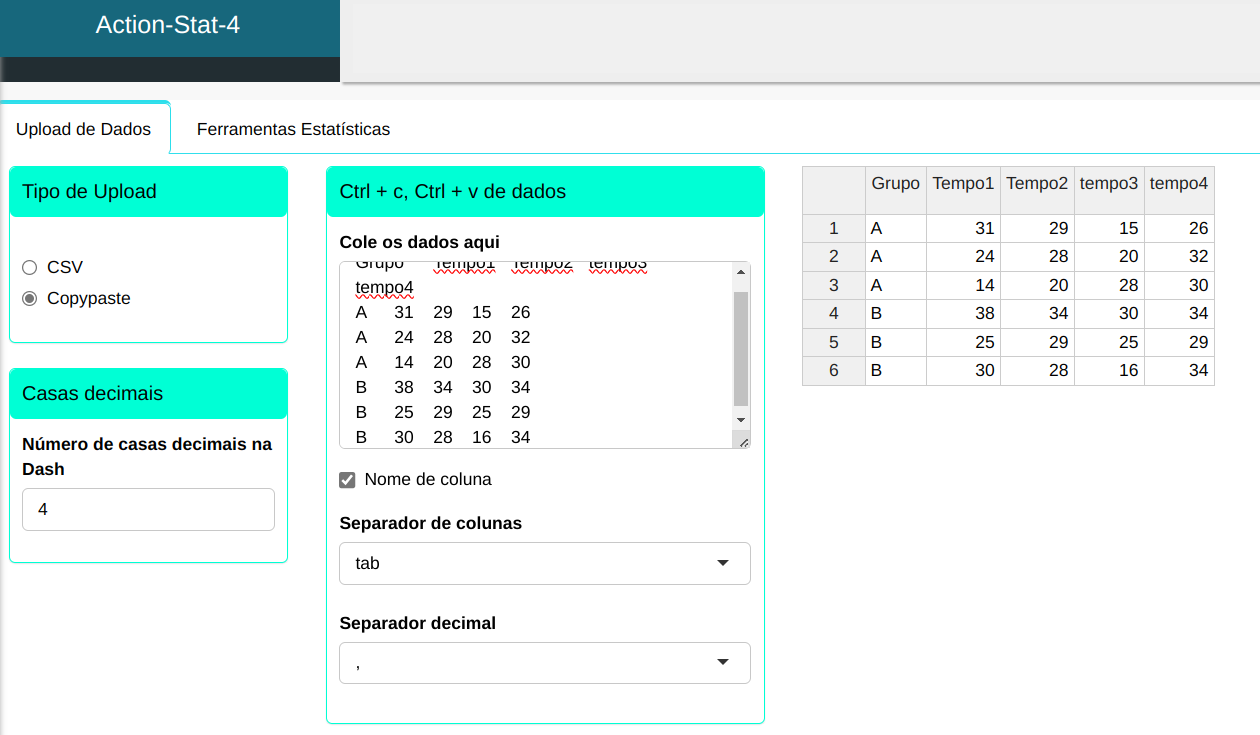
Fazemos a análise e configuramos de acordo com a figura abaixo.

Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Tabela das médias por grupo
| Grupos | Tempo1 | Tempo2 | Tempo3 | Tempo4 |
|---|---|---|---|---|
| A | 23 | 25.667 | 21.000 | 29.333 |
| B | 31 | 30.333 | 23.667 | 32.333 |
Matriz de Covariâncias
| Tempo1 | Tempo2 | Tempo3 | Tempo4 | |
|---|---|---|---|---|
| Tempo1 | 65.6 | 34.4 | -7.200 | 7.200 |
| Tempo2 | 34.4 | 20.4 | -0.800 | 3.800 |
| Tempo3 | -7.2 | -0.8 | 39.467 | 5.467 |
| Tempo4 | 7.2 | 3.8 | 5.467 | 9.767 |
Tabela da MANOVA
| G.L. | Estat.Wilks | Estat.F | G.L.Numerador | G.L.Denominador | P-valor | |
|---|---|---|---|---|---|---|
| Grupo | 1 | 0.508 | 0.242 | 4 | 1 | 0.888 |
| Resíduos | 4 |
Tabela da ANOVA : Tempo1
| G.L. | Soma de Quadrados | Quadrado Médio | Estat, F | P-valor | |
|---|---|---|---|---|---|
| Grupo | 1 | 96 | 96 | 1.655 | 0.268 |
| Resíduos | 4 | 232 | 58 |
Tabela da ANOVA : Tempo2
| G.L. | Soma de Quadrados | Quadrado Médio | Estat. F | P-valor | |
|---|---|---|---|---|---|
| Grupo | 1 | 32.667 | 32.667 | 1.885 | 0.242 |
| Resíduos | 4 | 69.333 | 17.333 |
Tabela da ANOVA : Tempo3
| G.L. | Soma de Quadrados | Quadrado Médio | Estat. F | P-valor | |
|---|---|---|---|---|---|
| Grupo | 1 | 10.667 | 10.667 | 0.229 | 0.658 |
| Resíduos | 4 | 186.667 | 46.667 |
Tabela da ANOVA : Tempo4
| G.L. | Soma de Quadrados | Quadrado Médio | Estat. F | P-valor | |
|---|---|---|---|---|---|
| Grupo | 1 | 13.500 | 13.500 | 1.528 | 0.,284 |
| Resíduos | 4 | 35.333 | 8.833 |