2. ANOVA Efeito Misto
A ANOVA é usada para analisar o comportamento de vários tratamentos de um fator aplicado ao processo e/ou produto.
Exemplo 1:
Considere o processo de medição do diâmetro do mancal de um motor. Os dados estão a seguir:
| Peças | Medições |
|---|---|
| 1 | 461,28 |
| 2 | 458,17 |
| 3 | 460,57 |
| 4 | 459,28 |
| 5 | 461,28 |
| 6 | 460,25 |
| 7 | 458,82 |
| 8 | 461,58 |
| 9 | 459,36 |
| 10 | 459,62 |
| 11 | 461,38 |
| 12 | 458,67 |
| 13 | 462,57 |
| 14 | 459,58 |
| 15 | 461,76 |
| 1 | 461,50 |
| 2 | 458,62 |
| 3 | 460,28 |
| 4 | 459,66 |
| 5 | 461,12 |
| 6 | 460,68 |
| 7 | 458,95 |
| 8 | 461,10 |
| 9 | 459,52 |
| 10 | 459,34 |
| 11 | 461,57 |
| 12 | 459,03 |
| 13 | 462,28 |
| 14 | 459,66 |
| 15 | 461,12 |
| 1 | 461,20 |
| 2 | 458,61 |
| 3 | 460,32 |
| 4 | 459,58 |
| 5 | 461,18 |
| 6 | 460,28 |
| 7 | 458,66 |
| 8 | 461,18 |
| 9 | 459,57 |
| 10 | 459,54 |
| 11 | 461,53 |
| 12 | 458,98 |
| 13 | 462,32 |
| 14 | 459,28 |
| 15 | 461,15 |
Faremos o upload dos dados no sistema.

Para realizar a ANOVA efeito misto, a seguinte configuração é realizada, conforme mostrado na figura a seguir.

Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
ANOVA com efeito aleatório - Modelo Restrito (Sigma > 0)
| Fatores | Desvio Padrão | X-squared | GL | P-valor | |
|---|---|---|---|---|---|
| X | Pecas | 1.18479 | 91.326 | 1 | 0 |
| X.1 | Resíduos | 0.19707 |
Intervalo de confiança do Efeito Peças
| Nível | Limite Inferior | Efeito para média | Limite Superior |
|---|---|---|---|
| 1 | 461.094 | 461.327 | 461.559 |
| 2 | 458.234 | 458.467 | 458.699 |
| 3 | 460.158 | 460.390 | 460.622 |
| 4 | 459.274 | 459.507 | 459.739 |
| 5 | 460.961 | 461.193 | 461.426 |
| 6 | 460.171 | 460.403 | 460.636 |
| 7 | 458.578 | 458.810 | 459.042 |
| 8 | 461.054 | 461.287 | 461.519 |
| 9 | 459.251 | 459.483 | 459.716 |
| 10 | 459.268 | 459.500 | 459.732 |
| 11 | 461.261 | 461.493 | 461.726 |
| 12 | 458.661 | 458.893 | 459.126 |
| 13 | 462.158 | 462.390 | 462.622 |
| 14 | 459.274 | 459.507 | 459.739 |
| 15 | 461.111 | 461.343 | 461.576 |
Testes de Normalidade - Resíduos
| Valor | |
|---|---|
| Média | 0 |
| Desvio Padrão | 0.163 |
| N | 45 |
| Anderson-Darling | 0.370 |
| P-Valor | 0.412 |
Testes de Normalidade - Intercepto Aleatório
| Valor | |
|---|---|
| Média | 0.000 |
| Desvio Padrão | 1.179 |
| N | 15.000 |
| Anderson-Darling | 0.516 |
| P-Valor | 0.159 |
A tabela liberada indica que as peças se diferenciam, já que o P-valor referente a esse fator (Peças) é menor que o nível de significância ($\alpha$) pré-determinado, de 5%.
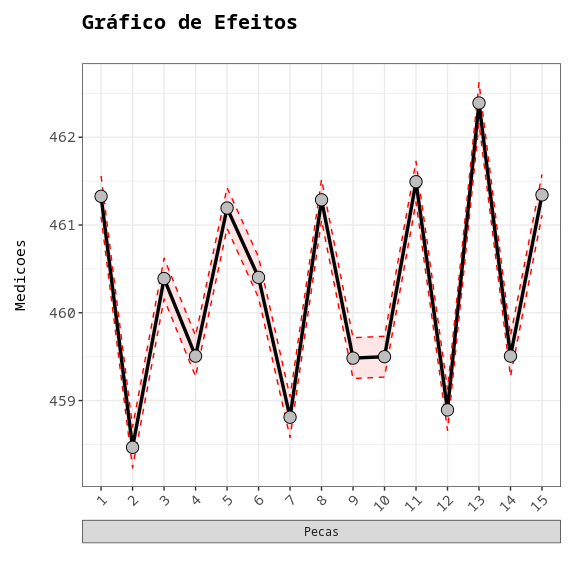
No gráfico, os pontos pretos, são as médias de cada nível do fator, que na tabela são denominados Efeitos. As linhas vermelhas representam o intervalo de confiança para as médias dos níveis do fator.
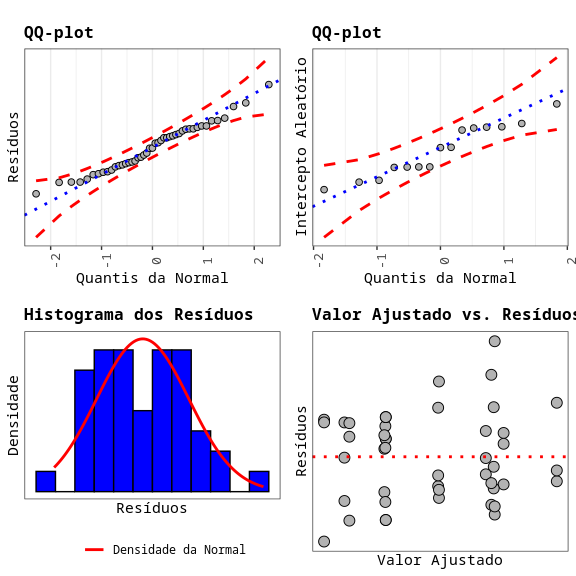
No gráfico 1: Gráfico de Resíduos versus Quantis da Normal.
No gráfico 2: Gráfico de Intercepto Aleatório versus Quantis da Normal.
No gráfico 3: Plotamos um histograma dos resíduos para termos ideia de como estão distribuídos os resíduos.
No gráfico 4: Gráfico de Resíduos versus valores ajustados.
No nosso caso, usaremos o teste de Anderson-Darling, onde a hipótese nula é de a normalidade dos dados, e pelo exemplo, verificamos não rejeitamos ("aceitamos") a hipótese nula e com isso verificamos a normalidade dos resíduos e do Intercepto Aleatório.
Exemplo 2:
Uma empresa deseja testar a diferença entre dois tipos de ração para cães. 24 animais seguiram a dieta e foram avaliados durante 6 dias. Nos primeiros 3 dias foi oferecido um tipo de ração e nos últimos 3 dias outro tipo.
| Animal | Raçao | Sequência | Período | Consumido |
|---|---|---|---|---|
| 1 | 1 | AB | 1 | 99,65 |
| 2 | 1 | AB | 1 | 43,97 |
| 3 | 1 | AB | 1 | 68,65 |
| 4 | 1 | AB | 1 | 77,50 |
| 5 | 1 | AB | 1 | 100,00 |
| 6 | 1 | AB | 1 | 100,00 |
| 7 | 1 | AB | 1 | 97,47 |
| 8 | 1 | AB | 1 | 29,58 |
| 9 | 1 | AB | 1 | 100,00 |
| 10 | 1 | AB | 1 | 100,00 |
| 11 | 1 | AB | 1 | 100,00 |
| 12 | 1 | AB | 1 | 31,62 |
| 13 | 2 | BA | 1 | 100,00 |
| 14 | 2 | BA | 1 | 45,73 |
| 15 | 2 | BA | 1 | 61,56 |
| 16 | 2 | BA | 1 | 99,40 |
| 17 | 2 | BA | 1 | 36,77 |
| 18 | 2 | BA | 1 | 100,00 |
| 19 | 2 | BA | 1 | 100,00 |
| 20 | 2 | BA | 1 | 100,00 |
| 21 | 2 | BA | 1 | 89,78 |
| 22 | 2 | BA | 1 | 74,10 |
| 23 | 2 | BA | 1 | 37,09 |
| 24 | 2 | BA | 1 | 36,08 |
| 1 | 2 | AB | 2 | 100,00 |
| 2 | 2 | AB | 2 | 0,00 |
| 3 | 2 | AB | 2 | 44,97 |
| 4 | 2 | AB | 2 | 43,15 |
| 5 | 2 | AB | 2 | 100,00 |
| 6 | 2 | AB | 2 | 100,00 |
| 7 | 2 | AB | 2 | 100,00 |
| 8 | 2 | AB | 2 | 16,49 |
| 9 | 2 | AB | 2 | 100,00 |
| 10 | 2 | AB | 2 | 100,00 |
| 11 | 2 | AB | 2 | 100,00 |
| 12 | 2 | AB | 2 | 19,10 |
| 13 | 1 | BA | 2 | 0,00 |
| 14 | 1 | BA | 2 | 80,80 |
| 15 | 1 | BA | 2 | 66,98 |
| 16 | 1 | BA | 2 | 100,00 |
| 17 | 1 | BA | 2 | 16,94 |
| 18 | 1 | BA | 2 | 100,00 |
| 19 | 1 | BA | 2 | 100,00 |
| 20 | 1 | BA | 2 | 100,00 |
| 21 | 1 | BA | 2 | 100,00 |
| 22 | 1 | BA | 2 | 75,09 |
| 23 | 1 | BA | 2 | 28,18 |
| 24 | 1 | BA | 2 | 13,07 |
Faremos o upload dos dados no sistema.

Para realizar a ANOVA efeito misto, a seguinte configuração é realizada, conforme mostrado na figura a seguir.
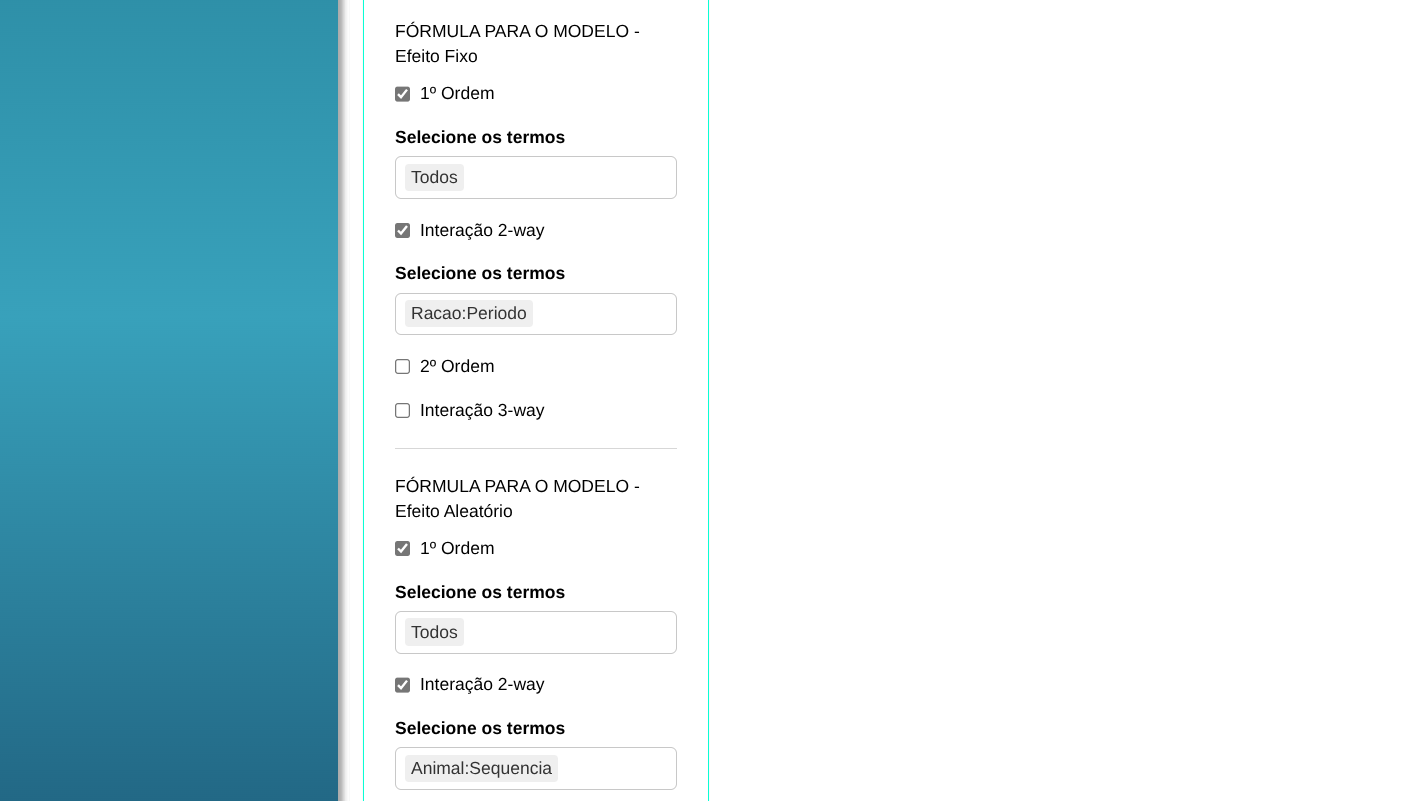

Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
ANOVA com efeito fixo
| GL Num. | GL Den. | Soma de Quadrados | Quadrados Médios | Estatística F | P-valor | |
|---|---|---|---|---|---|---|
| Animal | 1 | 20 | 4.6355 | 4.6355 | 0.0143 | 0.906 |
| Ração | 1 | 30.7161 | 11.2679 | 11.2679 | 0.0348 | 0.8533 |
| Sequência | 1 | 20.3385 | 30.252 | 30.252 | 0.0934 | 0.763 |
| Periodo | 1 | 374.6508 | 253.7175 | 253.7175 | 0.7831 | 0.3768 |
| Animal:Sequência | 1 | 20 | 48.2699 | 48.2699 | 0.149 | 0.7036 |
| Ração:Periodo |
ANOVA com efeito aleatório
| Fator | | Fator | Desvio Padrão | Correlação | X² | GL | P-valor | |
|---|---|---|---|---|---|---|---|
| X | Animal | (Intercepto) | 31.1448 | 17.7508 | 1 | 0 | |
| X.1 | Ração | (Intercepto) | 1.5657 | 0.000 | 1 | 1 | |
| X.2 | Sequência | (Intercepto) | 3.6907 | 0.000 | 1 | 1 | |
| X.3 | Periodo | (Intercepto) | 6.4968 | 0.000 | 1 | 1 | |
| X.4 | Resíduos | 17.9995 |

Intervalo de confiança do Efeito Animal
| Nível | Limite Inferior | Efeito para média | Limite Superior |
|---|---|---|---|
| 1 | 73.430 | 99.825 | 126.220 |
| 2 | -4.410 | 21.985 | 48.380 |
| 3 | 30.415 | 56.810 | 83.205 |
| 4 | 33.930 | 60.325 | 86.720 |
| 5 | 73.605 | 100.000 | 126.395 |
| 6 | 73.605 | 100.000 | 126.395 |
| 7 | 72.340 | 98.735 | 125.130 |
| 8 | -3.360 | 23.035 | 49.430 |
| 9 | 73.605 | 100.000 | 126.395 |
| 10 | 73.605 | 100.000 | 126.395 |
| 11 | 73.605 | 100.000 | 126.395 |
| 12 | -1.035 | 25.360 | 51.755 |
| 13 | 23.605 | 50.000 | 76.395 |
| 14 | 36.870 | 63.265 | 89.660 |
| 15 | 37.875 | 64.270 | 90.665 |
| 16 | 73.305 | 99.700 | 126.095 |
| 17 | 0.460 | 26.855 | 53.250 |
| 18 | 73.605 | 100.000 | 126.395 |
| 19 | 73.605 | 100.000 | 126.395 |
| 20 | 73.605 | 100.000 | 126.395 |
| 21 | 68.495 | 94.890 | 121.285 |
| 22 | 48.200 | 74.595 | 100.990 |
| 23 | 6.240 | 32.635 | 59.030 |
| 24 | -1.820 | 24.575 | 50.970 |
Intervalo de confiança do Efeito Sequência
| Nível | Limite Inferior | Efeito para média | Limite Superior |
|---|---|---|---|
| AB | 66.148 | 71.536 | 76.924 |
| BA | 66.148 | 71.536 | 76.924 |
Intervalo de confiança do Efeito Racao*Periodo
| Nível | Limite Inferior | Efeito para média | Limite Superior |
|---|---|---|---|
| 1|1 | 67.401 | 76.733 | 86.065 |
| 2|1 | 66.347 | 75.680 | 85.012 |
| 1|2 | 58.060 | 67.392 | 76.724 |
| 2|2 | 57.007 | 66.339 | 75.671 |


Outliers (Quantis)
| Obs. | Quantis da Normal | Resíduos | Critério |
|---|---|---|---|
| 13 | 2.31 | 42.313 | Envelope (Nível de Confiança=95%) |
| 37 | -2.31 | -49.400 | Envelope (Nível de Confiança=95%) |
| 14 | -1.62 | -23.180 | Envelope (Nível de Confiança=95%) |
| 31 | 1.32 | 9.987 | Envelope (Nível de Confiança=95%) |
| 4 | 1.45 | 10.234 | Envelope (Nível de Confiança=95%) |
Testes de Normalidade - Resíduos
| Valor | |
|---|---|
| Média | 0.000 |
| Desvio Padrão | 13.091 |
| N | 48.000 |
| Anderson-Darling | 1.438 |
| P-Valor | 0.001 |
Outliers (Quantis)
| Obs | Quantis da Normal | Intercepto Aleatório | Critério |
|---|---|---|---|
| 11 | 0.05 | 20.373 | Envelope (Nível de Confiança=95%) |
| 20 | 2.04 | 27.658 | Envelope (Nível de Confiança=95%) |
Testes de Normalidade - Intercepto Aleatório
| Valor | |
|---|---|
| Média | 0.000 |
| Desvio Padrão | 26.885 |
| N | 24.000 |
| Anderson-Darling | 1.598 |
| P-Valor | 0.000 |
Se o P-valor for menor ou igual ao nível de significância pré-determinado, significa que há diferença entre os dois tipos de ração, caso contrário, não há diferença. Neste caso, como os p-valores são maiores do que 0,05, não rejeitamos a hipótese nula de igualdade das rações, ou seja, podemos dizer que as rações não alteram a quantidade de consumo dos animais.
No gráfico, os pontos pretos, são as médias de cada nível do fator, que na tabela são denominados Efeitos. As linhas vermelhas representam o intervalo de confiança para as médias dos níveis do fator.
No gráfico 1: Gráfico de Resíduos versus Quantis da Normal.
No gráfico 2: Gráfico de Intercepto Aleatório versus Quantis da Normal.
No gráfico 3: Plotamos um histograma dos resíduos para termos ideia de como estão distribuídos os resíduos.
No gráfico 4: Gráfico de Resíduos versus valores ajustados.
No nosso caso, usaremos o teste de Anderson-Darling, onde a hipótese nula é de a normalidade dos dados, e pelo exemplo, verificamos não rejeitamos ("aceitamos") a hipótese nula e com isso verificamos a normalidade dos resíduos e do Intercepto Aleatório.