4. Testes de Comparações Múltiplas: Fisher
A estratégia Fisher é usada para realizar todas as comparações aos pares entre os níveis de um fator.
Exemplo 1:
Considere o processo de produção de uma fibra sintética, em que o experimentador quer conhecer a influência da porcentagem de algodão na resistência da fibra. Para isto, foi realizado um experimento totalmente aleatorizado, em que diversos níveis de porcentagem de algodão foram avaliados com respeito à resistência da fibra. Um ponto importante no planejamento do experimento é que para cada nível do fator (porcentagem de algodão), os outros fatores que influenciam o processo (como o meio ambiente, máquina, matéria-prima, etc.) devem apresentar um padrão homogêneo de variabilidade. No experimento, tomamos 5 níveis para a porcentagem de algodão e 5 replicações.
| Fator | Resistencia |
|---|---|
| 15 | 7 |
| 15 | 7 |
| 15 | 15 |
| 15 | 11 |
| 15 | 9 |
| 20 | 12 |
| 20 | 17 |
| 20 | 12 |
| 20 | 18 |
| 20 | 18 |
| 25 | 14 |
| 25 | 18 |
| 25 | 18 |
| 25 | 19 |
| 25 | 19 |
| 30 | 19 |
| 30 | 25 |
| 30 | 22 |
| 30 | 19 |
| 30 | 23 |
| 35 | 7 |
| 35 | 10 |
| 35 | 11 |
| 35 | 15 |
| 35 | 11 |
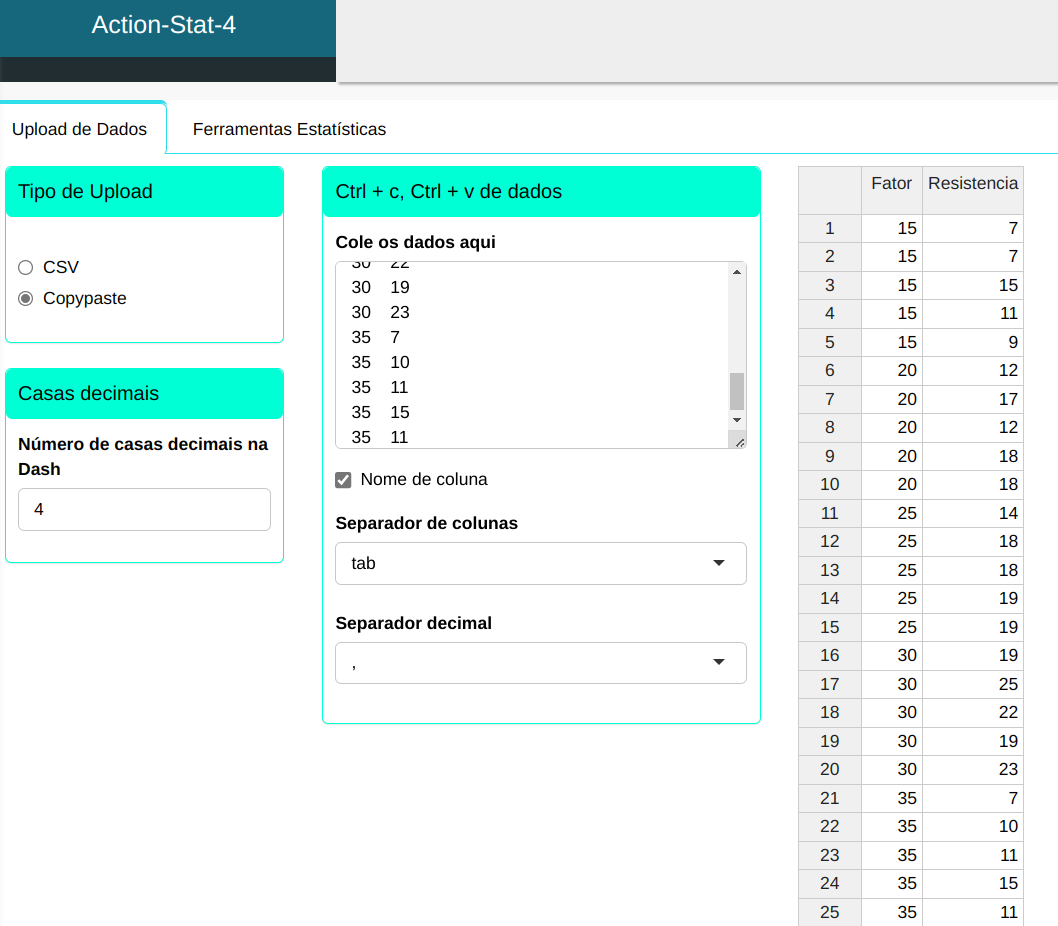
Faremos o teste de Fisher.
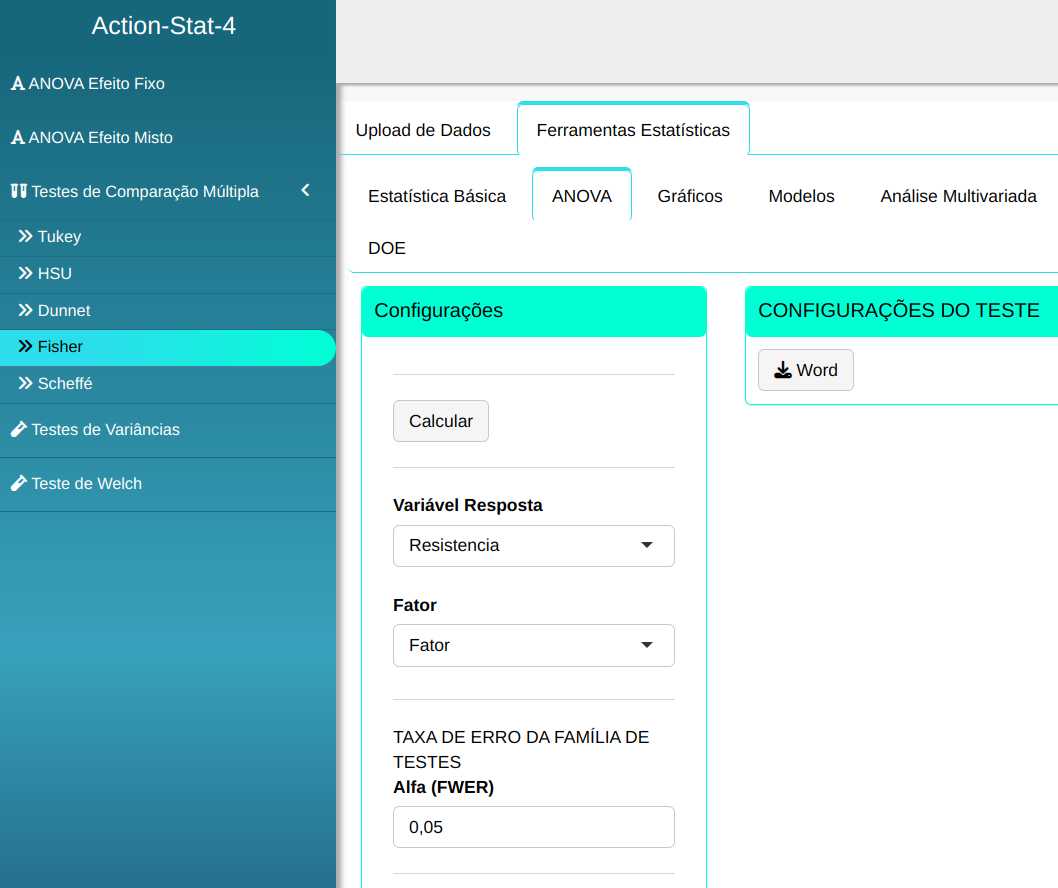
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultado são:
Resultado da análise
| Fator | Centro | Limite Inferior | Limite Superior | P-valor |
|---|---|---|---|---|
| 15-20 | -5.6 | -9.345 | -1.855 | 0.005 |
| 15-25 | -7.8 | -11.545 | -4.055 | 0.000 |
| 15-30 | -11.8 | -15.545 | -8.055 | 0.000 |
| 15-35 | -1.0 | -4.745 | 2.745 | 0.584 |
| 20-25 | -2.2 | -5.945 | 1.545 | 0.235 |
| 20-30 | -6.2 | -9.945 | -2.455 | 0.002 |
| 20-35 | 4.6 | 0.855 | 8.345 | 0.019 |
| 25-30 | -4.0 | -7.745 | -0.255 | 0.038 |
| 25-35 | 6.8 | 3.055 | 10.545 | 0.001 |
| 30-35 | 10.8 | 7.055 | 14.545 | 0.000 |
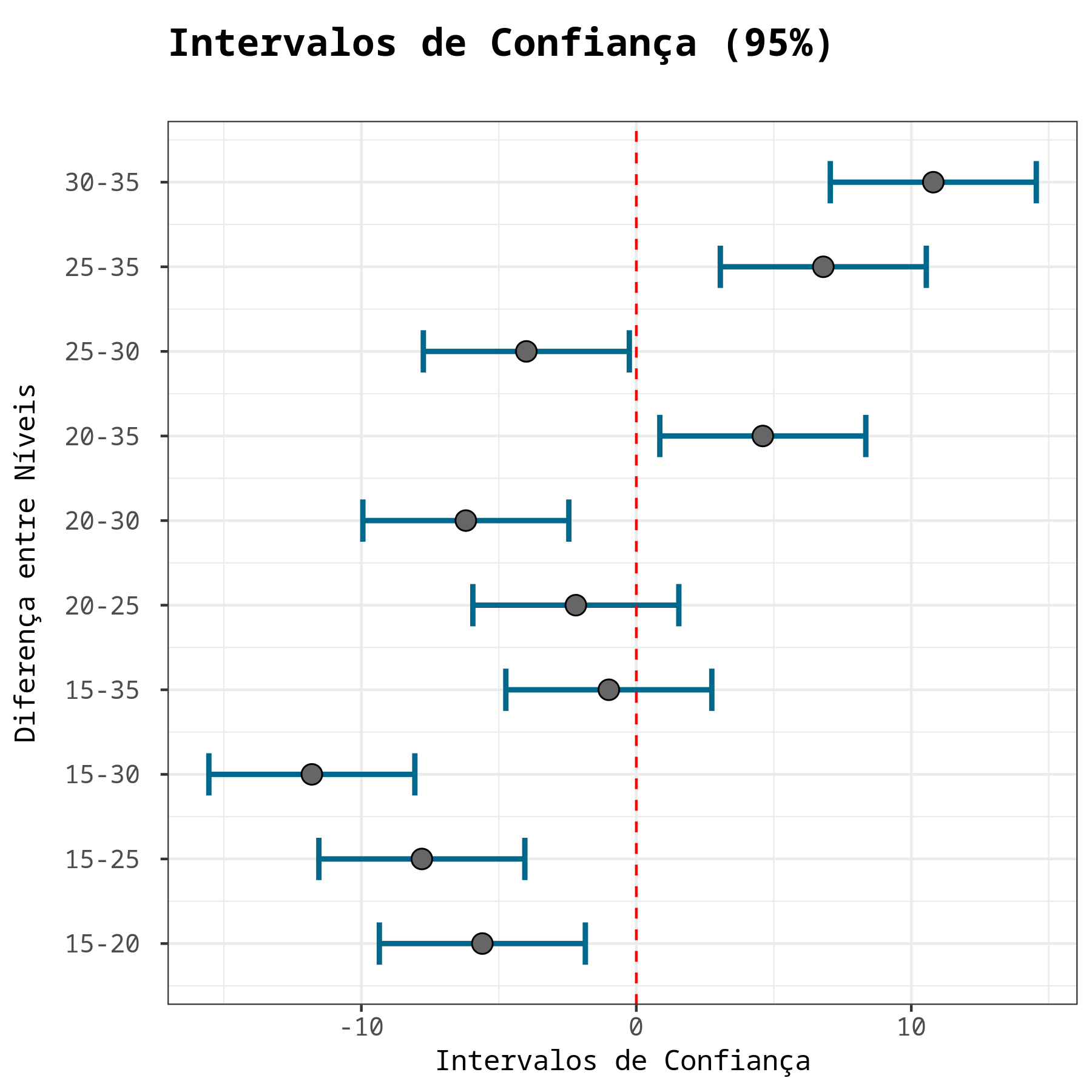
Como os testes anteriores, rejeitamos a igualdade entre as médias dos níveis se o P-valor é menor que alpha ou se o intervalo de confiança não conter o valor "zero" . Desta forma, no exemplo, rejeitamos a hipótese de igualdade entre os níveis para todas as comparações, exceto entre os níveis 15-35 e 20-25.
Exemplo 2:
Com os mesmos dados do Exemplo 1, agora aplicaremos o Teste de Fisher-Bonferroni.
| Fator | Resistencia |
|---|---|
| 15 | 7 |
| 15 | 7 |
| 15 | 15 |
| 15 | 11 |
| 15 | 9 |
| 20 | 12 |
| 20 | 17 |
| 20 | 12 |
| 20 | 18 |
| 20 | 18 |
| 25 | 14 |
| 25 | 18 |
| 25 | 18 |
| 25 | 19 |
| 25 | 19 |
| 30 | 19 |
| 30 | 25 |
| 30 | 22 |
| 30 | 19 |
| 30 | 23 |
| 35 | 7 |
| 35 | 10 |
| 35 | 11 |
| 35 | 15 |
| 35 | 11 |

Faremos o teste de Fisher
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultado são:
Resultado da análise
| Fator | Centro | Limite Inferior | Limite Superior | P-valor |
|---|---|---|---|---|
| 20-15 | 5.6 | -0.062 | 11.262 | 0.054 |
| 25-15 | 7.8 | 2.138 | 13.462 | 0.003 |
| 30-15 | 11.8 | 6.138 | 17.462 | 0.000 |
| 35-15 | 1.0 | -4.662 | 6.662 | 1.000 |
| 25-20 | 2.2 | -3.462 | 7.862 | 1.000 |
| 30-20 | 6.2 | 0.538 | 11.862 | 0.025 |
| 20-35 | 4.6 | -1.062 | 10.262 | 0.186 |
| 30-25 | 4.0 | -1.662 | 9.662 | 0.375 |
| 25-35 | 6.8 | 1.138 | 12.462 | 0.012 |
| 30-35 | 10.8 | 5.138 | 16.462 | 0.000 |
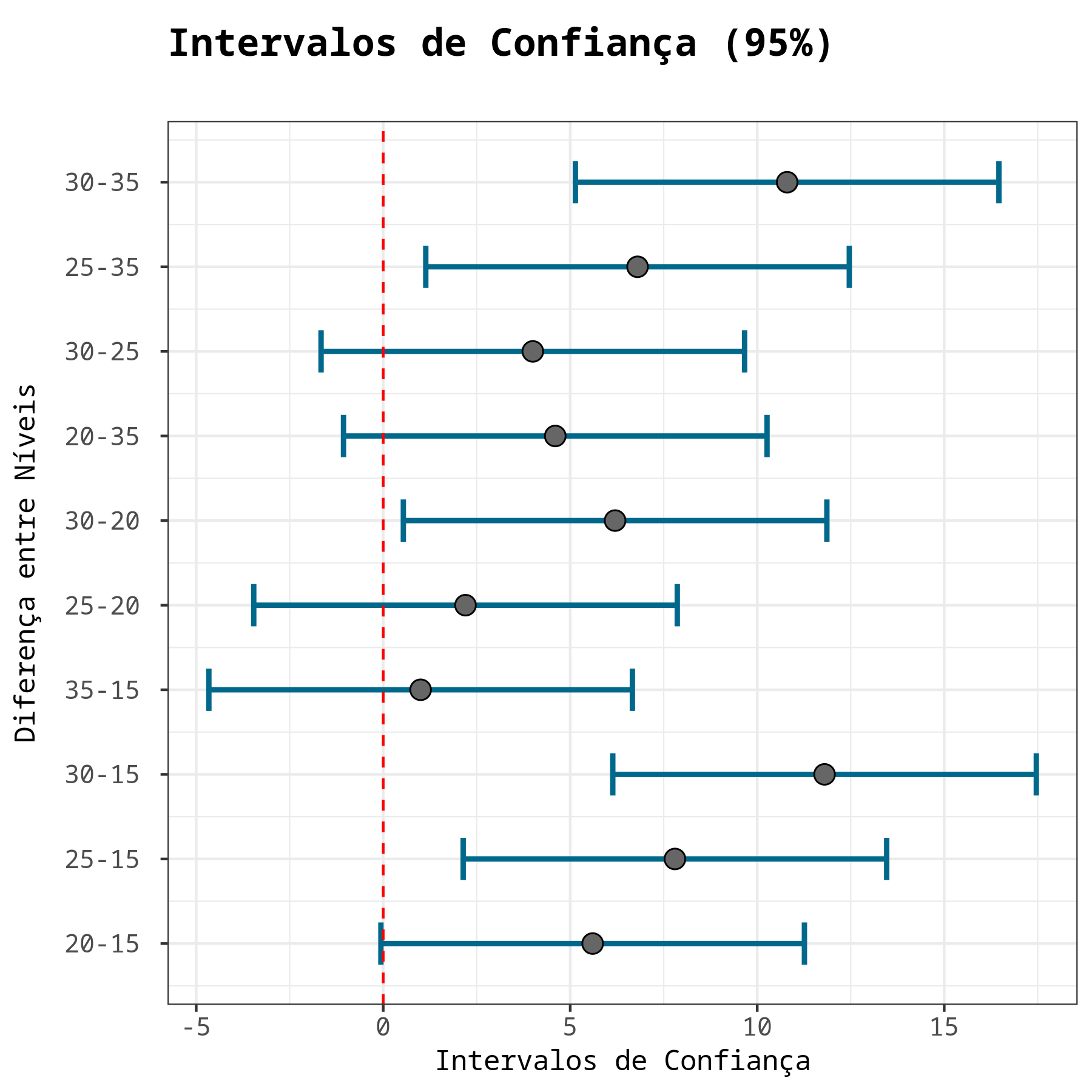
Ao considerarmos um nível de significância de 5% não rejeitamos a hipótese de igualdade entre as médias dos níveis: 20-15, 35-15, 25-20, 20-35 e 30-25.